回帰直線とは
組となるデータの、中心的な分布傾向を表す直線。
最小二乗法( least squares method )によって求められます。
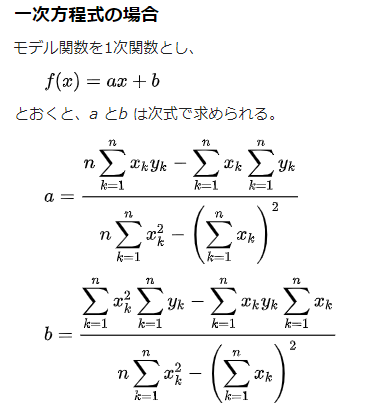
最小二乗法の式
📖最小二乗法(wikipedia)より引用
これを、javascript( ES6 )で関数化します。
Σをreduceで表現しています。
// 回帰直線を求める(最小二乗法)
const lsm = coordinates => {
const n = coordinates.length;
const sigX = coordinates.reduce((acc, c) => acc + c.x, 0);
const sigY = coordinates.reduce((acc, c) => acc + c.y, 0);
const sigXX = coordinates.reduce((acc, c) => acc + c.x * c.x, 0);
const sigXY = coordinates.reduce((acc, c) => acc + c.x * c.y, 0);
// a(傾き)を求める
const a = (n * sigXY - sigX * sigY) / (n * sigXX - Math.pow(sigX, 2));
// b(切片)を求める
const b = (sigXX * sigY - sigXY * sigX) / (n * sigXX - Math.pow(sigX, 2));
return { a, b };
}
👀動作確認
ドライバを作成して呼び出してみます。
const coordinates = [
{ x: 200, y: 100 },
{ x: 250, y: 150 },
{ x: 300, y: 150 },
{ x: 312, y: 200 },
{ x: 330, y: 210 },
{ x: 100, y: 80 },
{ x: 110, y: 40 },
]
const { a, b } = lsm(coordinates)
console.log(a, b)
結果
0.6227602344112315 -9.665985075256124
📈グラフを書いて確認
canvasにグラフを描画して確認してみました。
青のドットがサンプルデータ、赤が回帰直線です。
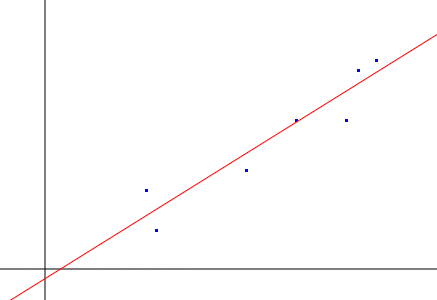
確認に使ったソースコードは以下です。
html
<html>
<head></head>
<body>
<canvas id="graph" width="500" height="500"></canvas>
<script type="text/javascript" src="main.js"></script>
</body>
</html>
javascript
main.js
// 回帰直線を求める(最小二乗法)
const lsm = coordinates => {
const n = coordinates.length
const sigX = coordinates.reduce((acc, c) => acc + c.x, 0)
const sigY = coordinates.reduce((acc, c) => acc + c.y, 0)
const sigXX = coordinates.reduce((acc, c) => acc + c.x * c.x, 0)
const sigXY = coordinates.reduce((acc, c) => acc + c.x * c.y, 0)
// a(傾き)を求める
const a = (n * sigXY - sigX * sigY) / (n * sigXX - Math.pow(sigX, 2));
// b(切片)を求める
const b = (sigXX * sigY - sigXY * sigX) / (n * sigXX - Math.pow(sigX, 2));
return { a, b }
}
const canvas = document.getElementById('graph');
if (canvas.getContext) {
const ctx = canvas.getContext('2d');
// x軸の描画
ctx.beginPath();
ctx.moveTo(100, 0);
ctx.lineTo(100, 500);
ctx.stroke();
// y軸の描画
ctx.beginPath();
ctx.moveTo(0, 400);
ctx.lineTo(500, 400);
ctx.stroke();
const coordinates = [
{ x: 200, y: 100 },
{ x: 250, y: 150 },
{ x: 300, y: 150 },
{ x: 312, y: 200 },
{ x: 330, y: 210 },
{ x: 100, y: 80 },
{ x: 110, y: 40 },
]
// サンプルデータの点を描画
ctx.fillStyle = "rgb(0, 0, 255)"
coordinates.forEach(c => {
ctx.fillRect(c.x + 100, -c.y + 400, 3, 3)
})
// 回帰直線の描画
const { a, b } = lsm(coordinates)
ctx.strokeStyle = "rgb(255, 0, 0)";
ctx.beginPath();
ctx.moveTo(-100 + 100, -(-100 * a + b) + 400);
ctx.lineTo(400 + 100, -(400 * a + b) + 400);
ctx.stroke();
}
コードのダウンロードはここ。
以上。