$$
\def\bra#1{\mathinner{\left\langle{#1}\right|}}
\def\ket#1{\mathinner{\left|{#1}\right\rangle}}
\def\braket#1#2{\mathinner{\left\langle{#1}\middle|#2\right\rangle}}
$$
本稿では、NISQを用いた量子系の時間発展計算アルゴリズムである「Variational Quantum Simulator」について紹介します。
背景
NISQ (Noisy Intermediate-Scale Quantum Computer) とは誤り訂正の機能を持たない(i.e., ノイズの影響を受けやすい)量子コンピュータのことです。
誤り訂正の機能を有する大規模な量子コンピュータの登場にはまだまだ年月がかかると考えられるため、より近い将来利用可能なNISQの応用が盛んに議論されています(NISQに関しては、例えば「 量子コンピュータの現在とこれから - Qmedia 」をご参照下さい)。
特に量子化学系へのNISQの応用が盛んに研究されており、VQE (Variational Quantum Eigensolver)や QAOA (Quantum Approximate Optimization Algorithm)といった手法が提案されています。
一方、量子系の時間発展のシミュレーションをNISQで行う例はあまり無いようです。
本稿では、NISQの弱点であるノイズを低減しつつ量子系の時間発展を計算するアルゴリズムである「Variational Quantum Simulator」を紹介します。
書誌情報
タイトル:Efficient Variational Quantum Simulator Incorporating Active Error Minimization
著者&所属:Ying Li and Simon C. Benjamin (University of Oxford)
発行日:29 June 2017
論文リンク:https://journals.aps.org/prx/abstract/10.1103/PhysRevX.7.021050
概要
量子系のダイナミクスを、量子コンピュータを用いてシミュレートする手法としてTrotterizationがありますが、これはNISQではない大規模な量子コンピュータの使用を前提としています。
本論文で提案されている、量子系の時間発展アルゴリズム「Variational Quantum Simulator」(以下ではVQSと略記します。)では、(VQEのように)計算の一部を古典コンピュータに担わせることで、エラー耐性を高め、NISQへの対応を図っています。
さらに、Trotterizationに比べてノイズに強いことが、数値計算によって確認されています。
何ができる?
- 与えられたハミルトニアンのもとで、ある初期状態の時間発展をシミュレートできる
- このモデルではエラーの発生確率を自由に変化させる事ができるため、ゼロエラーの場合の計算結果の推定値を外挿によって得ることも可能
先行手法(Trotterization)との比較
- hybrid algorithmは、Trotterizationを使う場合よりも遥かに小さい量子回路で計算できる
- しかし、Trotterizationよりも簡単な問題を考えていることに注意
- Trotterizationが任意の初期状態の時間発展を計算できる(即ち時間発展演算子が得られる)のに対し、VQSでは、「ある初期状態」を一つ指定し、その時間発展を計算している
- ある初期状態の時間発展だけで事足りる問題(わざわざ任意の初期状態の時間発展を求めなくてもよい問題)も多い
アルゴリズムの概要
VQSの計算アルゴリズムの概要を説明します。
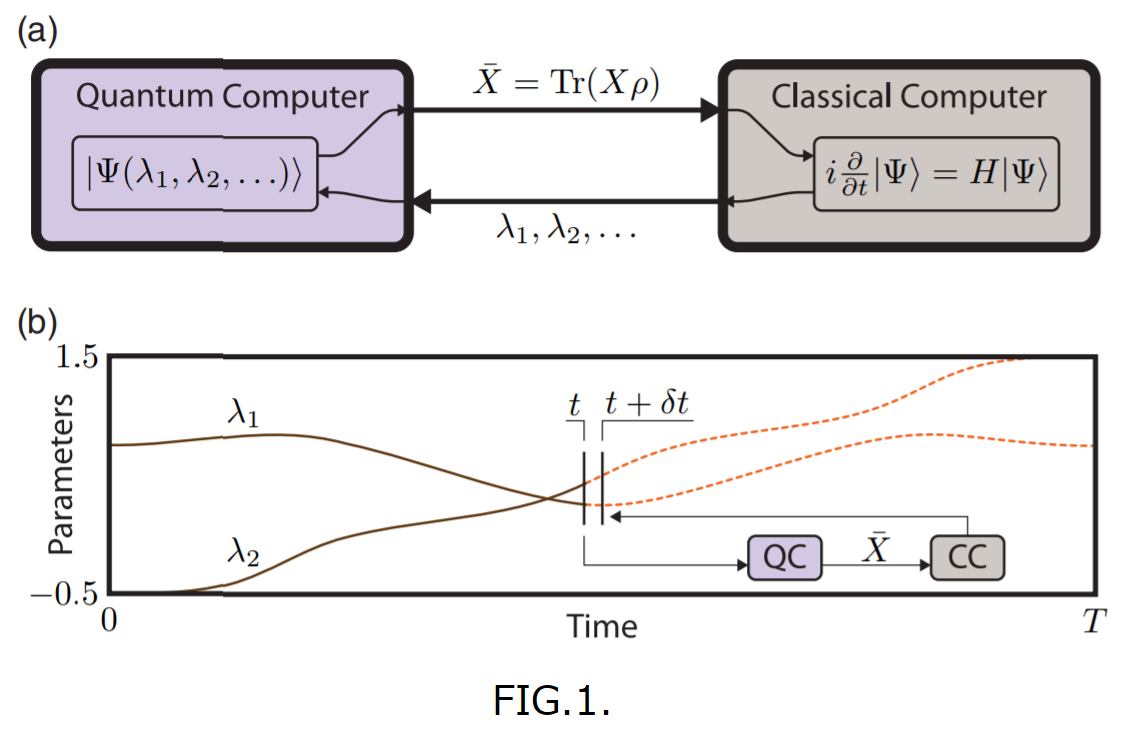
FIG.1(a)のように、量子/古典コンピュータが、交互に入力・出力をやりとりし、各時点$t$における状態$\ket{\Psi(t)}$を計算します。
ここで量子/古典コンピュータそれぞれの役割は、
- 量子コンピュータ(QC):CCから受け取ったパラメータの組$\{ \lambda(t)\}$ をもとに、FIG.1(a)の$\bar{X}$という量を計算
- 古典コンピュータ(CC):QCから受け取った値$\bar{X}$をシュレディンガー方程式に代入して解き、$\{ \lambda(t)\}$の時間微分を計算→新たなパラメータの組$\{\lambda(t+\delta t)\}$を得る
となっています。
より詳細な計算手続きを次節で説明します。
より具体的な計算手続き
ハミルトニアン$H$が与えられているとする。
- 考える時間幅$T$, 時間間隔$δt$を決定
- まず試行関数$\ket{Ψ}$を、パラメータ{λ}の関数として$\ket{Ψ(λ)} = R\ket{0} = R_N(\lambda_N) ... R_1(\lambda_1) \ket{0} \tag{7}$ で定義する(ここで$R_k \ (k=1,...,N)$は、それぞれパラメータ$\lambda_k$にのみ依存する行列)。
- パラメータの初期値$\{\lambda(t=0)\}$を決める
- 以下(a)~(e)を$t=0, \delta t,2\delta t, ..., T$で繰り返す
- (a) $\{\lambda(t)\}$を$\ket{Ψ}$に代入
- (b) QCを用いて、上の$\ket{Ψ}$から、以下のM, V を計算。計算式は$ M_{k,q} = i \eta \frac{\partial \bra{\Psi}}{\partial \lambda_{k}}\frac{\partial \ket{\Psi}}{\partial \lambda_{q}}+\rm{H.c.} \tag{5} $$V_{k} =\eta \frac{\partial \bra{\Psi}}{\partial \lambda_{k}} H \ket{\Psi}+\rm{H.c.} \tag{6}$
- (c) 係数M, Vを行列方程式(オイラー・ラグランジュ方程式:これはパラメータ$\{λ\}$に関する作用の変分を0と置くことで出てくる)(4)に代入
$\sum_{q} M_{k,q} \dot{\lambda_q} = V_{k} \tag{4} $ - (d) CCを用いてオイラー・ラグランジュ方程式(4)を解き、$\{\dot{\lambda}\}$を求める
- (e) $λ(t) \to λ(t+δt) = λ(t) + δt \ \dot{\lambda}(t) $ という更新式で、パラメータ$\{λ\}$を1ステップ更新。(a)に戻る
- 各ステップ$t$における、上記(a)で得られる$\ket{Ψ}$が求めたい状態である
係数M, Vの計算方法
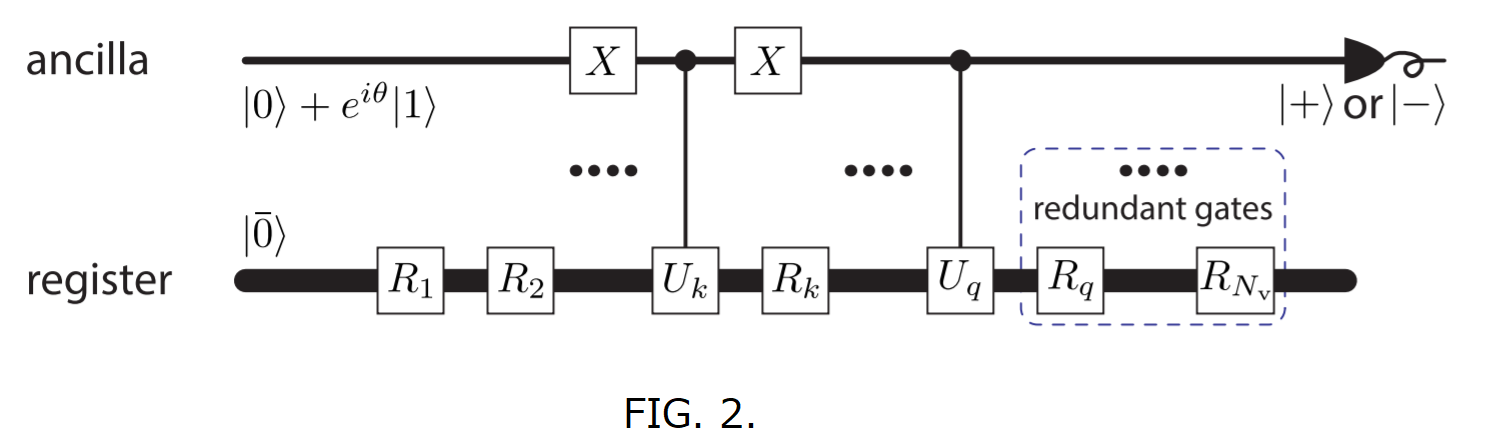
係数M, Vを計算する量子回路は下図(FIG.2)。
計算したい系のスピン数をNとすると、N個のレジスタ量子ビットと1個のアンシラ量子ビットが必要。
図のゲート操作を行うと、アンシラ量子ビットのX基底での測定値の期待値$\langle X\rangle = {\rm Tr}[\rho X]$がM, Vとなる。
ここでは量子操作・計測を複数セット行い平均を取ることで$\langle X\rangle$の値に代える。
数値計算結果
- 横磁場ありの量子イジングモデル(3スピン;周期境界条件)に対して時間発展を計算
- 実際の時間発展、Trotterization、VQS(error reductionあり/なし)の場合を、古典計算シミュレータを用いて比較
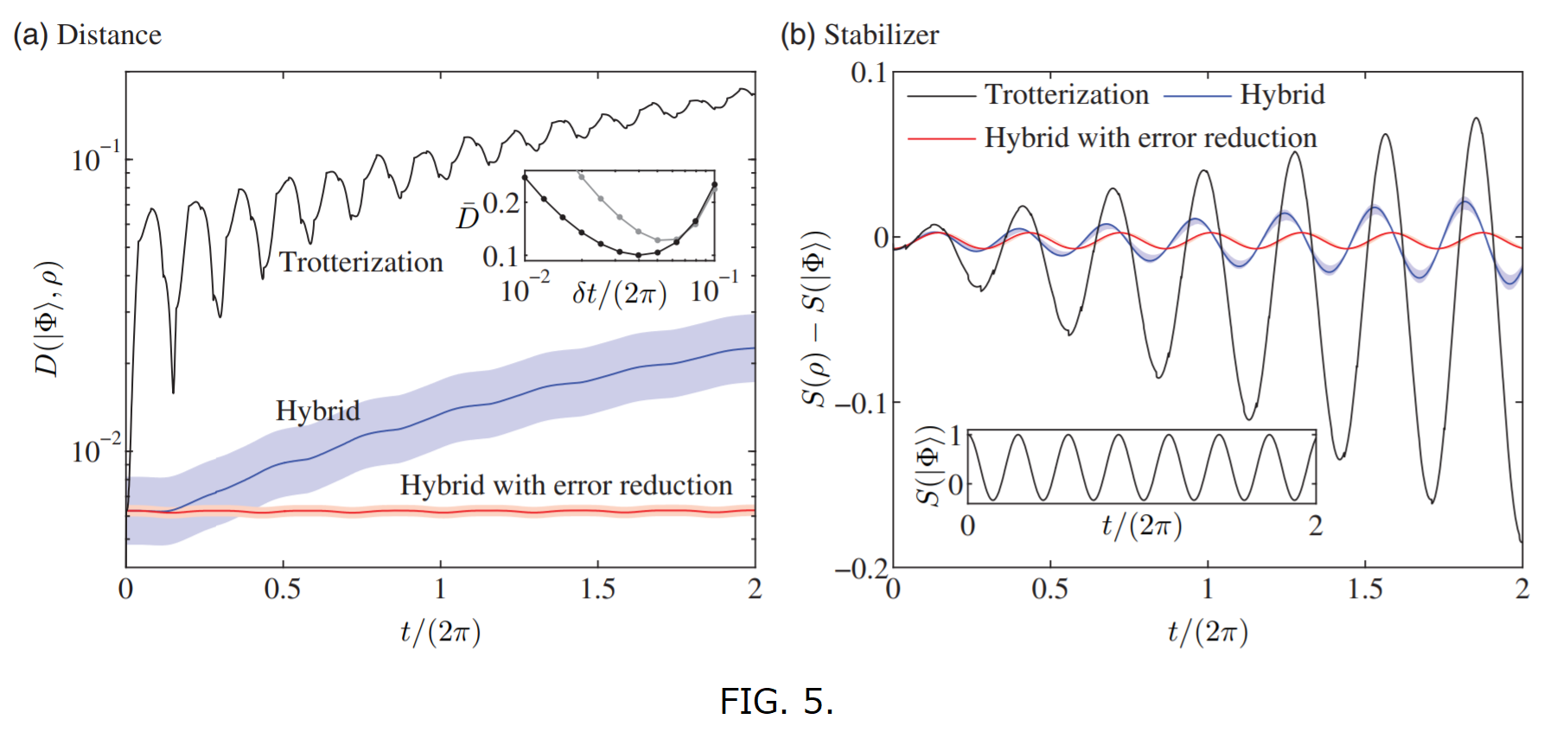
- FIG.5(a):
- 実際の時間発展$\ket{\Phi}$と、各計算手法(ノイズあり)により得られた状態$\rho$を比較
- 図の縦軸は、状態$\ket{\Phi}$と状態$\rho$の間の距離(トレース距離)→小さいほど良い
- Trotterizationzに比べ、VQSによるシミュレーションの精度が高いことがわかる
- FIG.5(b):
- 2番目のスピンに対するスタビライザー演算子$S_2$の期待値の時間発展(の、真の値からの乖離)
- insetは真の値のプロット
- Trotterizationに比べ、時間が経過しても正しい値からの差が小さいことがわかる
数値計算セットアップの詳細
- 必要な量子ビット数は$3+1=4$
- 初期状態$\ket{\Phi(0)}$は1次元クラスター状態に取る。
- クラスター状態は、各スピンを$\ket{+}$としておき、繋がっているスピンのペアそれぞれにCZゲートをかけることで得られる
- ここで初期状態をクラスター状態に取るのは、試行関数$\ket{\Psi} = e^{i\lambda_2 H_{\rm X}} e^{i\lambda_1 H_{\rm Z}} \ket{\Phi(0)}$
で、実際の時間発展の解析解を表せるようにするためと考えられる
- ノイズはdepolarizing noise (参考:http://www.kurims.kyoto-u.ac.jp/~kyodo/kokyuroku/contents/pdf/2059-01.pdf) を仮定している
- error reductionは、エラーの発生確率を人為的に変化させ、ゼロエラーの場合の計算結果を外挿によって得るという手続きである
- 参考:量子回路の高速シミュレーター「Qulacs」を用いたerror mitigationの実装例 (https://github.com/qulacs/quantum-circuits/blob/master/error_mitigation/NoiseMitigation_Japanese.ipynb)
考察
VQSは、NISQで量子系のダイナミクスを計算するための一つの良い手法であると考えられます。
しかし、上で触れた通り、Trotterizationでは時間発展の行列をまとめて計算するのに対し、VQSでは1つの状態しか一度にシミュレートできない、というデメリットがあります。
少数の状態がドミナントである現象に用いるには便利そうです。