概要
量子フロケ系とは、時間依存ハミルトニアン$H(t)$が時間$T$の周期を有している量子系のことです。
H(t + T) = H(t)
量子系のシミュレーションパッケージであるQuTiPには、フロケ系のシミュレーションに必要なツールが揃っているので、それを使ってみます。
理論的背景
時間依存するハミルトニアン系のシュレディンガー方程式は次のように書けます。
i \hbar \frac{d}{dt} |\psi(t)\rangle = H(t) |\psi(t)\rangle
この解は時間発展演算子$U(t_2, t_1)$を用いて
|\psi(t)\rangle = U(t, 0)|\psi(0)\rangle
と書けます。ただし、
U(t_2, t_1):= \mathcal{T}\left[ \exp \left(-\frac{i}{\hbar} \int_{t_1}^{t_2} ds H(s) \right)\right]
であり、$\mathcal{T}$は時間順序積を表します。
時間発展演算子の性質
$t_1$から$t_2$までの時間発展と、$t_2$から$t_3$までの時間発展を合わせると$t_1$から$t_3$までの時間発展となるので、次の式が成り立ちます。
U(t_3, t_2)U(t_2, t_1)= U(t_3, t_1)
また$H$の周期性から、$U(t_2, t_1)$の$T$の時間並進に対する不変性がわかります。
\begin{align}
U(t_2+T, t_1+T) &= \mathcal{T}\left[ \exp \left(-\frac{i}{\hbar} \int_{t_1+T}^{t_2+T} ds H(s) \right)\right] \\
& = \mathcal{T}\left[ \exp \left(-\frac{i}{\hbar} \int_{t_1}^{t_2} ds H(s + T) \right)\right] \\
& = \mathcal{T}\left[ \exp \left(-\frac{i}{\hbar} \int_{t_1}^{t_2} ds H(s ) \right)\right] \\
& = U(t_2, t_1)
\end{align}
フロケの定理
$U(T, 0)$はユニタリ演算子なので、あるエルミート演算子$H_F$を用いて、
U(T, 0) = \exp(-i H_F T/\hbar)
と表すことができます。また、$U(t,0)\exp(i H_F t/\hbar)$もユニタリ演算子なので、時刻$t$に依存するあるエルミート演算子$K_F(t)$を用いて、
U(t,0)\exp(i H_F t/\hbar) = \exp(-i K_F(t)/\hbar)
と表すことができます。以上より、
U(t,0) = \exp(-i K_F(t)/\hbar)\exp(-i H_F t/\hbar)
が成り立ちます。
ここで、
\begin{align}
U(t+T,0) & = U(t+T, T)U(T, 0)\\
& = U(t, 0)U(T, 0)\\
& = \exp(-i K_F(t)/\hbar)\exp(-i H_F t/\hbar)\exp(-i H_F T/\hbar)\\
& = \exp(-i K_F(t)/\hbar)\exp(-i H_F\times (t+T)/\hbar)
\end{align}
であり、左辺は$\exp(-i K_F(t+T)/\hbar)\exp(-i H_F\times (t+T)/\hbar)$であることに注意すると、$K_F(t)$の周期性
K_F(t+T) = K_F(t)
がわかります。
$H_F$の固有値を{$\epsilon_n$}、固有状態を{$|n\rangle$}とし、初期状態$|\psi(0)\rangle$を{$|n\rangle$}で展開したときの係数を{$a_n$}と置いてみます。
|\psi(0)\rangle = \sum_n a_n |n\rangle
時刻$t$の状態$|\psi(t)\rangle$は、
\begin{align}
|\psi(t)\rangle & = U(t, 0)|\psi(0)\rangle \\
&= \sum_n a_n U(t,0)|n\rangle \\
&= \sum_n a_n \exp(-i K_F(t)/\hbar)\exp(-i H_F t/\hbar)|n\rangle \\
&= \sum_n a_n \exp(-i K_F(t)/\hbar)\exp(-i \epsilon_n t/\hbar)|n\rangle \\
&= \sum_n a_n \exp(-i \epsilon_n t/\hbar) |u_n(t)\rangle \\
\end{align}
となります。ただし、
|u_n(t)\rangle := \exp(-i K_F(t)/\hbar)|n\rangle
であり、$K_F(t)$の周期性から、$|u_n(t)\rangle$も周期性を持ちます。
|u_n(t+T)\rangle =|u_n(t)\rangle
このように$|\psi(t)\rangle$が周期$T$を持つ$|u_n(t)\rangle$を用いて$\exp(-i \epsilon_n t/\hbar) |u_n(t)\rangle $の重ね合わせで書けることを、フロケの定理と言います。
以上より、数値計算において$|\psi(t)\rangle$は次の手順で求めることができます。
- $U(T,0)$を計算し、対角化することで{$\epsilon_n$}、{$|n\rangle$}を求める。
- $t\in [0, T]$に対して$|u_n(t)\rangle = \exp(i \epsilon_n t/\hbar) U(t, 0)|n\rangle$ を求める。
- $|\psi(0)\rangle$の{$|n\rangle$}による展開係数{$a_n$}を求め、$|\psi(t)\rangle = \sum_n a_n \exp(- i \epsilon_n t/\hbar) |u_n(t')\rangle$を計算する。ただし、$t'\in [0, T]$は$t$を$T$で割った余り。
QuTiPでの計算
次のハミルトニアンを取り扱います。
H(t)=− \frac{\Delta}{2} \sigma_x − \frac{\epsilon_0}{2} \sigma_z + \frac{A}{2} \sin(\omega t)\sigma_z.
まず{$|n\rangle = |u_n(0)\rangle$}と{$\epsilon_n$}を求めてみましょう。2次元なので2つの固有状態と固有値が生じます。
import numpy as np
from qutip import *
import matplotlib.pyplot as plt
delta = 0.2 * 2*np.pi
eps0 = 1.0 * 2*np.pi
A = 2.5 * 2*np.pi
omega = 1.0 * 2*np.pi
T = 2*np.pi / omega
H0 = - delta/2.0 * sigmax() - eps0/2.0 * sigmaz()
H1 = A/2.0 * sigmaz()
H = [H0, [H1, 'sin(w * t)']] # H0 + H1*sin(w*t)の意味。時間依存項を表すQuTipの記法。
args = {'w': omega} # これをfloquet_modesの引数に渡すと、wにomegaが代入される。
f_modes_0, f_energies = floquet_modes(H, T, args)
print(f_energies)
print(f_modes_0[0].data)
print(f_modes_0[1].data)
実行結果
[-2.83131212 2.83131212]
(0, 0) (0.72964231187078+0j)
(1, 0) (-0.39993745864107016+0.5546820043084018j)
(0, 0) (0.39993745864107005+0.5546820043084018j)
(1, 0) (0.72964231187078+0j)
{$\epsilon_n$}は定義上$2\pi \hbar /T$の整数倍の任意性がありますが、QuTiPでは$-\pi\hbar /T \le \epsilon_n \le \pi\hbar /T$に制限されているようです。f_modes_0はQobjクラスのリストです。data属性で量子状態のスパース行列を取得できます。
次に時間発展を計算してみましょう。
初期状態を
|\psi(0)\rangle =
\begin{pmatrix}
1\\
0
\end{pmatrix}
として、展開係数{$a_n$}を計算してみます。
psi0 = basis(2,0)
f_coeff = floquet_state_decomposition(f_modes_0, f_energies, psi0)
print(f_coeff)
実行結果
[(0.72964231187078+0j), (0.39993745864107005-0.5546820043084018j)]
引数のf_energiesは別に必要ないし、フロケとも関係ない関数ですが、QuTiPで与えられた基底で展開係数求めるのはこの関数しかないようです…
状態$|\psi(t)\rangle $は次のように計算できます。
psi_t = floquet_wavefunction_t(f_modes_0, f_energies, f_coeff, 1, H, T, args) #時刻1での状態
print(psi_t.data)
実行結果
(0, 0) (-0.952247951725807+0.019771617832092026j)
(1, 0) (-0.2471425782149468-0.17819502685421923j)
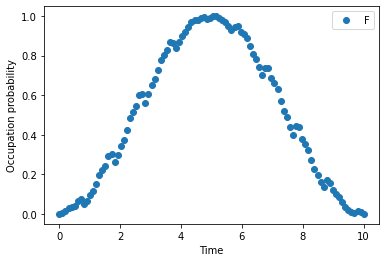
最後に数演算子$N := \sigma_+ \sigma_-$の期待値を$t \in [0, 10T]$の範囲でプロットしてみます。
tlist = np.linspace(0.0, 10 * T, 101)
p_ex = np.zeros(len(tlist))
for n, t in enumerate(tlist):
psi_t = floquet_wavefunction_t(f_modes_0, f_energies, f_coeff, t, H, T, args)
p_ex[n] = expect(num(2), psi_t)
plt.plot(tlist, real(p_ex), 'o')
plt.xlabel('Time')
plt.ylabel('Occupation probability')
plt.legend(("Floquet $P_1$"))
plt.show()
参考リンク
QuTiP公式チュートリアル
https://qutip.org/docs/4.1/guide/dynamics/dynamics-floquet.html
Konrad Viebahn, Introduction to Floquet theory (2020).
https://boulderschool.yale.edu/sites/default/files/files/floquetlecture_Konrad%20Viebahn.pdf