【一般相対性理論】近日点移動のシミュレーション

測地線方程式をシュミレーションして、惑星の近日点移動をみてみる、という記事です。
こういうアニメーションを作ります。

本記事のコードをjupyter-notebookにまとめたものです。

#測地線方程式
曲がった時空中の質点の運動は測地線方程式で記述できます。

\frac{d^2x^{\alpha}}{d\lambda^2}+\Gamma^{\alpha}_{\mu \nu} \frac{dx^{\mu}}{d\lambda} \frac{dx^{\nu}}{d\lambda}=0

$\Gamma^{\alpha}_{\mu \nu}$はクリストッフェル記号と呼ばれ、採用している座標系が局所慣性座標系からどれほどずれているかを表す量です。

\Gamma_{\mu \nu}^{\alpha}=\frac{1}{2} g^{\alpha \beta}\left(\frac{\partial g_{\nu \beta}}{\partial x^{\mu}}+\frac{\partial g_{\beta \mu}}{\partial x^{\nu}}-\frac{\partial g_{\mu \nu}}{\partial x^{\beta}}\right)

#クリストッフェル記号の計算

以下計量は$(-, +, +, +)$を採用します。
シュワルツシルト解の計量

ds^2 = -\left(1 - \frac{2M}{r} \right)dt^{2} + \left(1 - \frac{2M}{r} \right)^{-1}dr^2 + r^2 (d\theta^2 + \sin^2{\theta} d\phi^2)

のクリストッフェル記号を計算してみます。この場合は手で計算できますが、今後より複雑な計量にも対応できるように

GraviPy

に計算してもらいましょう。
公式ドキュメントはgithubレポジトリのdocsディレクトリにあるipnbファイルです。

qiitaに解説記事もあるようです。

from gravipy.tensorial import *
from sympy import *

t, r, theta, phi, M = symbols('t, r, theta, phi, M')
chi = Coordinates('\chi', [t, r, theta, phi])
Metric = diag(-(1-2*M/r), 1/(1-2*M/r), r**2, r**2*sin(theta)**2)  #Schwarzschild計量
g = MetricTensor('g', chi, Metric)
Ga = Christoffel('Ga', g)

テンソルの要素にアクセスするには

Ga(-2, 3, 2)

などとします。$t,r,\theta,\phi$が順に1から4に対応し、正の数は下付き添字（共変テンソル）を、負の数は上付き添字（反変テンソル）を表します。上の例は$\Gamma^{r}_{\theta \phi}$となります。

#測地線方程式の計算
次に測地線方程式による四元加速度

a^{\alpha}  = \frac{d^2x^{\alpha}}{d\lambda^2}= -\Gamma^{\alpha}_{\mu \nu} \frac{dx^{\mu}}{d\lambda} \frac{dx^{\nu}}{d\lambda} =  -\Gamma^{\alpha}_{\mu \nu} v^{\mu}v^{\nu}

を計算しましょう。ここで$\lambda$は測地線のパラメータです(固有時ではないです)。

from itertools import product
var("v_0, v_1, v_2, v_3")
var("a_0, a_1, a_2, a_3")
a_list = [a_0, a_1, a_2, a_3]
v_list = [v_0, v_1, v_2, v_3]
for i in range(4):
    a_list[i] = 0
for i, j, k in product(range(4), repeat=3):
    a_list[i] -= Ga( -i-1, j + 1, k + 1)*v_list[j]*v_list[k]

シュミレーションするに当たってsympyの数式に数値を代入するより、関数に数値を代入するほうが早いので、関数化しておきます。

参考:

from sympy.utilities.lambdify import lambdify
a_func = lambdify((t, r, theta, phi, M, v_0, v_1, v_2, v_3), a_list)

位置と速度の四元ベクトル$x^\mu, v^\mu$を入力すると四元加速度$a^\mu$を返す関数を定義します。

import numpy as np
# M=1の場合
def a(x, v): return np.array(a_func(x[0], x[1], x[2], x[3], 1, v[0], v[1], v[2], v[3]))

Runge–Kutta法

時間発展はRunge–Kutta法(wikipedia)で計算します。

ニュートン運動方程式のRunge–Kutta法によるシュミレーションを参考にしました。

今解きたい問題は、

\begin{align}
&\frac{dv^\mu}{d\lambda} = a^\mu(x^\mu, v^\mu)\\
&\frac{dx^\mu}{d\lambda} = v^\mu
\end{align}

なので

\begin{align}
&k^\mu_{1v} = a^\mu(x^\mu, v^\mu)d\lambda \\
&k^\mu_{1x} = v^\mu d\lambda \\
&k^\mu_{2v} = a^\mu(x^\mu + \frac{k^\mu_{1x}}{2}, v^\mu+ \frac{k^\mu_{1v}}{2})d\lambda\\
&k^\mu_{2x} = ( v^\mu+ \frac{k^\mu_{1v}}{2})d\lambda \\
&k^\mu_{3v} = a^\mu(x^\mu + \frac{k^\mu_{2x}}{2}, v^\mu+ \frac{k^\mu_{2v}}{2})d\lambda\\
&k^\mu_{3x} = ( v^\mu+ \frac{k^\mu_{2v}}{2})d\lambda\\
&k^\mu_{4v} = a^\mu(x^\mu + k^\mu_{3x}, v^\mu + k^\mu_{3v})d\lambda\\
&k^\mu_{4x} = (v^\mu + k^\mu_{3v})d\lambda
\end{align}

を計算して、$x^\mu$, $v^\mu$を

\begin{align}
x^\mu_{\mathrm{next}} = x^\mu + \frac{1}{6}(k^\mu_{1x} + 2k^\mu_{2x} + 2k^\mu_{3x} + k^\mu_{4x}) \\
v^\mu_{\mathrm{next}} = v^\mu + \frac{1}{6}(k^\mu_{1v} + 2k^\mu_{2v} + 2k^\mu_{3v} + k^\mu_{4v})
\end{align}

と更新します。
ニュートン運動方程式の時刻$t$に相当するのが測地線のパラメータ$\lambda$です。

N = 10**5 #計算ステップ数

x = np.array([0.0, 17.32050808,  0.95531662, -0.78539816]) #初期位置
v = np.array([1, -0.02886728, -0.00824957,  0.01750001]) #初期速度

dlam = 0.1 #1ステップごとに進む\lambda幅
R = [] 
Theta = []
Phi = []
T = []
for _ in range(N):
    T.append(x[0])
    R.append(x[1])
    Theta.append(x[2])
    Phi.append(x[3])
    k1v = a(x, v)*dlam
    k1x = v*dlam
    k2v = a(x+k1x/2, v+k1v/2)*dlam
    k2x = (v+k1v/2)*dlam
    k3v = a(x+k2x/2, v+k2v/2)*dlam
    k3x = (v+k2v/2)*dlam
    k4v = a(x+k3x, v+k3v)*dlam
    k4x = (v+k3v)*dlam
    v = v + (1/6)*(k1v+2*k2v+2*k3v+k4v)
    x = x + (1/6)*(k1x+2*k2x+2*k3x+k4x)
X = R*np.cos(Phi)*np.sin(Theta)
Y = R*np.sin(Phi)*np.sin(Theta)
Z = R*np.cos(Theta)

初期値の選び方の注意

初期値の選び方にはいくつか注意があります。
a_list[3]を見てみると、

- \frac{v_{2} v_{3} \sin{\left(2 \theta \right)}}{\sin^{2}{\left(\theta \right)}} - \frac{2 v_{1} v_{3}}{r}

となっていて、$\theta=0, \pi$のときに0/0の計算が生じることがわかります。
対処法は2つあります。1つは$\theta$成分の計算をしないという方法です。シュヴァルツシルト計量は等方的なので、軌道の角運動量が保存します。従って軌道は同一平面上に存在するので、$\theta$の自由度は最初から計算しなくても大丈夫です。ただしこの方法は等方的な計量の場合に限られます。
もう1つは$\theta$の初期値を$\theta=0, \pi$以外に取るという方法です。時間発展して$\theta=0, \pi$に近づく瞬間はあれど厳密に等しくなることは確率的にほとんどないので、初期値だけ$\theta=0, \pi$を避ければ良いです。
今後非等方的な(角運動量が保存しない)計量でも計算をすることも考え、後者の方法を取ることにします。
また$r$成分は、シュヴァルツシルト半径が$2M$であることに注意して、それよりは大きく取ります。
速度については、$t=0$付近で$\lambda = t$と$\lambda$を選ぶと$\frac{dt}{d\lambda}=1$なので時間成分の速度は1にします。空間成分の速度は遅すぎると事象の地平面へ落ちてしまいますし、速すぎると重力場を脱出してしまいます。ちょうど良い塩梅で選びます。

##パラメータの変換

今、謎のパラメータ$\lambda$で$x$, $y$, $z$がパラメーター付けされているので、$t$によるパラメータ付けに変える必要があります。時系列データの補間をします。

参考：

dt = 10 #時間幅
T_new = np.arange(0, T[-1], dt)
X_new = np.interp(T_new, T, X)
Y_new = np.interp(T_new, T, Y)
Z_new = np.interp(T_new, T, Z)

アニメーションの実装

%matplotlib nbagg
import matplotlib.pyplot as plt 
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation

fig = plt.figure()
ax = fig.add_subplot(111, projection="3d")
L = 50
def update(i):
    ax.clear()
    ax.scatter(0, 0, 0, marker="o", c="orange", s=100)
    ax.plot(X_new[:i], Y_new[:i], Z_new[:i], c="black", alpha = 0.4)
    ax.scatter(X_new[i], Y_new[i], Z_new[i], marker="o", c="blue", s=10)
    ax.set_title(r"$t=$"+str(int(T_new[i])))
    ax.view_init(elev=30, azim=225)
    ax.set_xlim(-L, L)
    ax.set_ylim(-L, L)
    ax.set_zlim(-L, L)

ani = animation.FuncAnimation(fig, update, frames=len(T_new), interval=1)

##結果

近日点移動が見えますね！

#固有時の計算
せっかくなので、質点の固有時(質点とともに運動する観測者の時間)も計算してみます。質点が$dx^\mu$だけ動いたとき、世界間隔は

ds^2 = g_{\mu \nu} dx^\mu dx^\nu

で計算できます。
変位$dx^\mu$に対応する固有時の変化$d\tau$は

d\tau = \sqrt{-ds^2} = \sqrt{-g_{\mu \nu} dx^\mu dx^\nu}

で与えられます(なお根号の中の符号は計量のとり方によって変わります。$(+,-,-,-)$の場合は$+$です)。
これを積分すると固有時が求められます。

\tau = \int d\tau

$a^\mu$と同様に、位置と変位の四元ベクトル$x^\mu, dx^\mu$を入力すると固有時の差分$d\tau$を返す関数を定義します。

var("ds2, dx_0, dx_1, dx_2, dx_3")
dx_list = [dx_0, dx_1, dx_2, dx_3]
ds2 = 0
for i, j in product(range(4), repeat=2):
    ds2 += g(i+1,j+1)*dx_list[i]*dx_list[j]
ds2_func = lambdify((t, r, theta, phi, M, dx_0, dx_1, dx_2, dx_3), ds2)
def dtau(x, dx): return np.sqrt(-ds2_func(x[0], x[1], x[2], x[3], 1, dx[0], dx[1], dx[2], dx[3]) + 0j)

固有時$\tau$を計算するコードを含めてもう一度シュミレーションしてみます。

N = 10**5
x = np.array([0.0, 17.32050808,  0.95531662, -0.78539816])
v = np.array([1, -0.02886728, -0.00824957,  0.01750001])
dlam = 0.1
R = [] 
Theta = []
Phi = []
T = []
tau = 0  #固有時
Tau = []

for _ in range(N):
    Tau.append(tau)
    T.append(x[0])
    R.append(x[1])
    Theta.append(x[2])
    Phi.append(x[3])
    k1v = a(x, v)*dlam
    k1x = v*dlam
    k2v = a(x+k1x/2, v+k1v/2)*dlam
    k2x = (v+k1v/2)*dlam
    k3v = a(x+k2x/2, v+k2v/2)*dlam
    k3x = (v+k2v/2)*dlam
    k4v = a(x+k3x, v+k3v)*dlam
    k4x = (v+k3v)*dlam
    v = v + (1/6)*(k1v+2*k2v+2*k3v+k4v)
    x = x + (1/6)*(k1x+2*k2x+2*k3x+k4x)
    tau = tau + dtau(x, (1/6)*(k1x+2*k2x+2*k3x+k4x))
X = R*np.cos(Phi)*np.sin(Theta)
Y = R*np.sin(Phi)*np.sin(Theta)
Z = R*np.cos(Theta)

dt = 10 #時間幅
T_new = np.arange(0, T[-1], dt)
X_new = np.interp(T_new, T, X)
Y_new = np.interp(T_new, T, Y)
Z_new = np.interp(T_new, T, Z)
R_new = np.interp(T_new, T, R)
Tau_new = np.interp(T_new, T, Tau)
Dtau_new = np.diff(Tau_new) #dtごとのd\tau

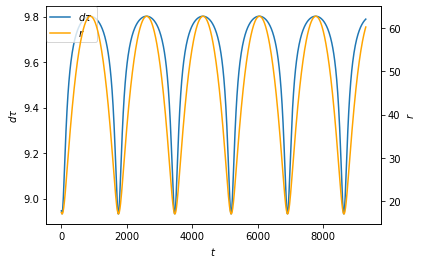
$dt$ごとの固有時$d\tau$と$r$の関係をプロットしてみます。

%matplotlib inline
fig = plt.figure()
ax1 = fig.add_subplot(111)
ax2 = ax1.twinx()
ax1.plot(T_new[:-1], Dtau_new.real, label=r"$d\tau$")
ax2.plot(T_new[:-1], R_new[:-1], c="orange", label=r"$r$")
ax1.set_xlabel(r"$t$")
ax1.set_ylabel(r"$d\tau$")
ax2.set_ylabel(r"$r$")
handler1, label1 = ax1.get_legend_handles_labels()
handler2, label2 = ax2.get_legend_handles_labels()
ax1.legend(handler1 + handler2, label1 + label2, loc=2, borderaxespad=0.)

重力源に近づくほど($r$が小さいほど)、固有時がゆっくり流れる($d\tau$が小さくなる)ということがわかります。重力による時間の遅れが見えました！

事象の地平面へ落ちる場合

質点が事象の地平面へ落ちる様子もみてみます。事象の地平面$r=2M$で計算が破綻するので、
正確な数値計算を行うことは難しいです。以下の計算はあまり正確ではないです。

$d\lambda=0.01 | r - 2M|$と事象の地平面に近づくのに合わせて$d\lambda$を小さくします。
それでもFloatingPointErrorが起こるのでそこで計算を止めます。

N = 10**5
x = np.array([0, 4,  np.pi/2, 0]) 
v = np.array([1, 0, 0,  0.11])

dlam = 0.01
R = [] 
Theta = []
Phi = []
T = []
tau = 0  #固有時
Tau = []

np.seterr(all="raise") #WarningをErrorにする
for _ in range(N):
    try:
        #事象の地平面に近づいたらd\lambdaを小さくする
        dlam = 0.01*(np.abs(x[1] - 2))
        Tau.append(tau)
        T.append(x[0])
        R.append(x[1])
        Theta.append(x[2])
        Phi.append(x[3])
        k1v = a(x, v)*dlam
        k1x = v*dlam
        k2v = a(x+k1x/2, v+k1v/2)*dlam
        k2x = (v+k1v/2)*dlam
        k3v = a(x+k2x/2, v+k2v/2)*dlam
        k3x = (v+k2v/2)*dlam
        k4v = a(x+k3x, v+k3v)*dlam
        k4x = (v+k3v)*dlam
        v = v + (1/6)*(k1v+2*k2v+2*k3v+k4v)
        x = x + (1/6)*(k1x+2*k2x+2*k3x+k4x)
        tau = tau + dtau(x, (1/6)*(k1x+2*k2x+2*k3x+k4x))
    except FloatingPointError:
        break
dt = 1 #時間幅
T_new = np.arange(0, T[-1], dt)
R_new = np.interp(T_new, T, R)
Tau_new = np.interp(T_new, T, Tau)
Dtau_new = np.diff(Tau_new) #dtごとのd\tau

アニメーションの実装

%matplotlib nbagg
fig = plt.figure()
ax = fig.add_subplot(111)
circle_phi = np.linspace(0, 2*np.pi, 100)
circle_x = 2*np.cos(circle_phi)
circle_y = 2*np.sin(circle_phi)
L = 4 #描画する空間のサイズ
def update(i):
    ax.clear()
    ax.plot(circle_x, circle_y, c="black")
    ax.scatter(X_new[i], Y_new[i], marker="o", c="blue", s=1)
    ax.set_title(r"$t=$"+str(int(T_new[i]))+"\t"+r"$\tau=$"+str(round(Tau_new[i].real,2)))
    ax.set_xlim(-L, L)
    ax.set_ylim(-L, L)
    ax.set_aspect('equal')

ani = animation.FuncAnimation(fig, update, frames=len(T_new), interval=100)

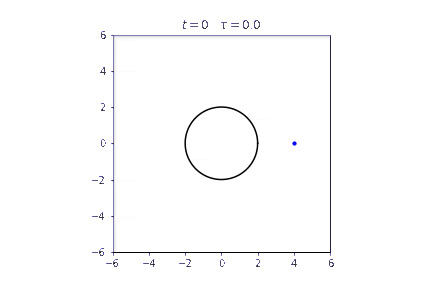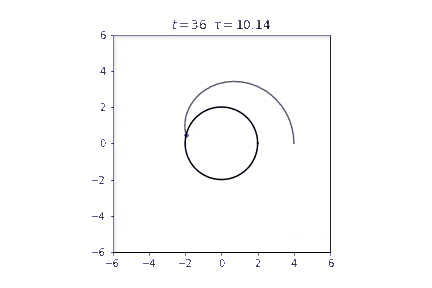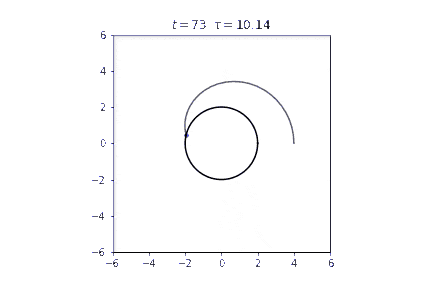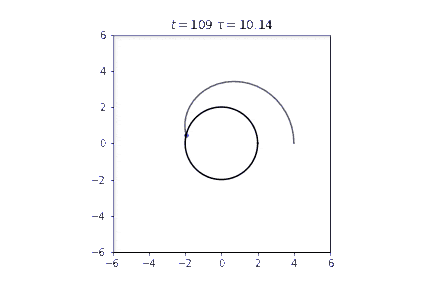
##結果

最初重力を受けて加速しますが、事象の地平面に近づくと減速し、事象の地平面の前に張り付いてしまいます。その状態では固有時はほとんど進みません。
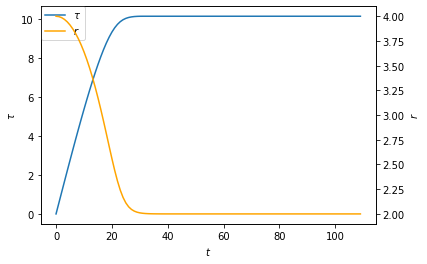
$t, r, \tau$の関係もみてみましょう。

%matplotlib inline
fig = plt.figure()
ax1 = fig.add_subplot(111)
ax2 = ax1.twinx()
ax1.plot(T_new,Tau_new.real, label=r"$\tau$")
ax2.plot(T_new, R_new, c="orange", label=r"$r$")
ax1.set_xlabel(r"$t$")
ax1.set_ylabel(r"$\tau$")
ax2.set_ylabel(r"$r$")
handler1, label1 = ax1.get_legend_handles_labels()
handler2, label2 = ax2.get_legend_handles_labels()
ax1.legend(handler1 + handler2, label1 + label2, loc=2, borderaxespad=0.)

最後に

githubの方にはKerr計量の場合も載せています。クリストッフェル記号は自動で計算してくれるので、別の計量でも特に変更を加えることなくシュミレーションできます。

ぜひ計量を変えていろいろ遊んでみて下さい！