概要
コンテスト中に公式の解説動画にある棚式を考え出したものの、勘違いでできないと判断してしまった(^^;
別の置き方を考え出す必要があり、その結果。
下記を踏まえたもの。
- 問題にある通り、順序を変えてはいけない
- 問題にある通り、入力値には誤差があるため座標的な位置を特定することはできない
- 得点の計算式から正方形に近くなる方が良い
- 問題にある通り、置き方指示はかなりの縛りがある
案1
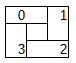
問題の例からヒントを得たもので、4つセットで置く。
下図の向きで置く。
そしてこれを再帰的に行う。
どういうことかというと、最初はこれで0~3の物が置かれる。
次はこのセットを1つの物とみなす。
このため、4は下図になり、16は更にこれ全体を1つの物とみなすので、5の右になる。
案2
物の最大数は100。
とすると、案1だと、べき乗ではなく中途の場合は横長になってしまう。
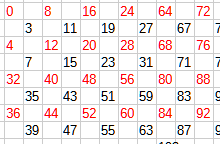
例えば92だと下図。
(黒字は置き方に使用する物。)
64以降を左右均等にするのが下図。
が、今思えば、更に小さいべき乗の場合も起こる(笑)
例えば、28とか。
案3
案2の最後の均等置きを利用して、下図のように全て均等置き。
案4
この均等置きは、セットではなく1コずつの場合で最初の方に思いついた。
ただ、1コで行った場合、下図のようになってしまうと思ったために却下した。
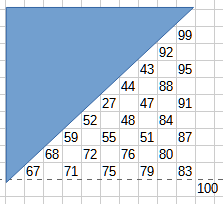
ただこれは、斜辺全部を対象にした場合で、交互に1つだけ、2つ前を対象とすると、スライドが発生してこのようにはならないだろうと思った。
その場合の置き方が下図。
最終的には4つの中ではこれが一番良い得点になった。