#きっかけ
同じ研究室のメンバーの方から、分散共分散行列の逐次更新がしたいけど何かいい方法はないか、という相談を受けました。そこで見つけたのがこの記事。ここでは平均と分散の逐次更新に関する式の導出を行っています。そこの部分に関する詳しい内容は当該サイトを参照してください。
ここでは、このサイトでは詳細に触れられなかった共分散に関する式の導出を行い、分散共分散行列をPython3で計算します。
#共分散の導出
###文字と重要な式の確認
導出する前に使用する文字や関係式を書いておきます。結構な量の変形をしますので、式を追う途中で分からなくなったらここに戻って考えてみてください。
データ
$x=(x_1,x_2,\ ...\ ,x_n),\ y=(y_1,y_2,\ ...\ ,y_n)$
データの平均
$\overline{x_n}=\frac{1}{n}\sum_{i=1}^nx_i\ ,\ \overline{y_n}=\frac{1}{n}\sum_{i=1}^ny_i$
共分散
$s_{xy}^{n}=\frac{1}{n}\sum_{i=1}^n{\left(x_i\ -\ \overline{x_n}\ \right)\left(y_i\ -\ \overline{y_n}\ \right)}$
平均値に関する漸化式
$\overline{x_{n+1}}\ -\ \overline{x_{n}}\ =\ \frac{1}{n+1}\left(x_{n+1}\ -\ \overline{x_n}\right)\cdots\star$
###共分散の漸化式を導出
さあ本題です!ここから式をいじっていきますが、粘り強くついてきてくださいね!
$M_n=ns_{xy}^n$ として、$M_{n+1}-M_n$ の計算を行います。これが求まれば共分散の漸化式は簡単に求められますから。
\begin{align}
M_{n+1}-M_n &= \sum_{i=1}^{n+1}\left(x_i\ -\ \overline{x_{n+1}}\ \right)\left(y_i\ -\ \overline{y_{n+1}}\ \right) -\sum_{i=1}^n\left(x_i\ -\ \overline{x_n}\ \right)\left(y_i\ -\ \overline{y_n}\ \right)\\
&= \sum_{i=1}^{n+1}\left(x_iy_i\ -\ x_i\overline{y_{n+1}}\ -\ \overline{x_{n+1}}y_i\ +\ \overline{x_{n+1}}\ \overline{y_{n+1}}\right)\\
&\ -\sum_{i=1}^n\left(x_iy_i\ -\ x_i\overline{y_{n}}\ -\ \overline{x_{n}}y_i\ +\ \overline{x_{n}}\ \overline{y_{n}}\right)\\
&=x_{n+1}y_{n+1}\ +\ (n+1)\overline{x_{n+1}}\ \overline{y_{n+1}}\ -\ n\overline{x_n}\ \overline{y_n}\\
&\ -\underline{\left(\overline{y_{n+1}}\sum_{i=1}^{n+1}x_i\ +\ \overline{x_{n+1}}\sum_{i=1}^{n+1}y_i\ -\ \overline{y_{n}}\sum_{i=1}^nx_i\ -\ \overline{x_{n}}\sum_{i=1}^ny_i\right)}\cdots\ast
\end{align}
さて、ここまで大丈夫ですか?ここで一旦下線を引いた部分を(1)としてここの計算をしていきましょう。
簡単のために次の2つの文字を導入します。
$A_n=\sum_{i=1}^nx_i\ ,\ B_n=\sum_{i=1}^ny_i$
さあ、(1)を片付けて行きましょう!
\begin{align}
(1) &=\overline{y_{n+1}}\ A_{n+1}\ +\ \overline{x_{n+1}}\ B_{n+1}\ -\ \overline{y_n}\ A_n\ -\ \overline{x_n}\ B_n\\
&=2\left(\frac{1}{n+1}A_{n+1}B_{n+1}\ -\ \frac{1}{n}A_nB_n\right)\\
&=2\left\{(n+1)\ \overline{x_{n+1}}\ \overline{y_{n+1}}\ -\ n\ \overline{x_n}\ \overline{y_n}\right\}
\end{align}
はい、きれいになりました!これを先ほどの下線部に代入して行きましょう。
\begin{align}
\ast&=x_{n+1}y_{n+1}\ +\ (n+1)\ \overline{x_{n+1}}\ \overline{y_{n+1}}\ -\ n\ \overline{x_n}\ \overline{y_n}-2\left\{(n+1)\ \overline{x_{n+1}}\ \overline{y_{n+1}}\ -\ n\ \overline{x_n}\ \overline{y_n}\right\}\\
&=x_{n+1}y_{n+1}\ -(n+1)\ \overline{x_{n+1}}\ \overline{y_{n+1}}\ +\ n\ \overline{x_n}\ \overline{y_n}\\
&=x_{n+1}y_{n+1}\ -(n+1)\underline{\left(\overline{x_{n+1}}\ \overline{y_{n+1}}\ -\ \overline{x_n}\ \overline{y_n}\right)}\ -\ \overline{x_n}\ \overline{y_n}\cdots\ast\ast
\end{align}
2つ目の下線です。ここを(2)として計算していきます。
\begin{align}
(2)&=\left(\overline{x_{n+1}}\ -\ \overline{x_n}\right)\left(\overline{y_{n+1}}\ -\ \overline{y_n}\right)+\overline{x_{n+1}}\ \overline{y_n}+\overline{x_{n}}\ \overline{y_{n+1}}\ -2\ \overline{x_{n}}\ \overline{y_n}\\
&=\left(\overline{x_{n+1}}\ -\ \overline{x_n}\right)\left(\overline{y_{n+1}}\ -\ \overline{y_n}\right)+\overline{y_n}\left(\overline{x_{n+1}}\ -\overline{x_n}\right)+\overline{x_n}\left(\overline{y_{n+1}}\ -\overline{y_n}\right)\\
&=\frac{x_{n+1}-\overline{x_n}}{n+1}\cdot \frac{y_{n+1}-\overline{y_n}}{n+1}+ \overline{y_n}\ \frac{x_{n+1}-\overline{x_n}}{n+1}+\overline{x_n}\ \frac{y_{n+1}-\overline{y_n}}{n+1}\ (\because\ \star)\\
&=\frac{1}{n+1}\left\{ \frac{1}{n+1}\left(x_{n+1}-\overline{x_n}\right)\left(y_{n+1}-\overline{y_n}\right)+\overline{y_n}\ \left(x_{n+1}-\overline{x_n}\right)+\overline{x_n}\ \left(y_{n+1}-\overline{y_n}\right)\right\}
\end{align}
さあ、あともう少しでゴールです!
\begin{align}
\ast\ast&=x_{n+1}y_{n+1}\ -\frac{1}{n+1}\left(x_{n+1}-\overline{x_n}\right)\left(y_{n+1}-\overline{y_n}\right)-\overline{y_n}\ \left(x_{n+1}-\overline{x_n}\right)-\overline{x_n}\ \left(y_{n+1}-\overline{y_n}\right)-\overline{x_n}\ \overline{y_n}\\
&=\frac{n}{n+1}\ x_{n+1}y_{n+1}\ -\ \frac{n}{n+1}\ x_{n+1}\overline{y_n}\ -\ \frac{n}{n+1}\ \overline{x_n}\ y_{n+1}\ +\frac{n}{n+1}\ \overline{x_n}\ \overline{y_n}\\
&=\frac{n}{n+1}\ \left(x_{n+1}\ -\ \overline{x_n}\right)\ \left(y_{n+1}\ -\ \overline{y_n}\right)
\end{align}
これでメインの変形は終了です。最後の仕上げをしていきます。
\begin{align}
M_{n+1}-M_n&=\frac{n}{n+1}\left(x_{n+1}\ -\ \overline{x_n}\right)\left(y_{n+1}\ -\ \overline{y_n}\right)\\
\therefore\ M_{n+1} &= \frac{n}{n+1}\left(x_{n+1}\ -\ \overline{x_n}\right)\left(y_{n+1}\ -\ \overline{y_n}\right)\ +\ M_n\\
\therefore\ s_{xy}^{n+1}\ &=\ \frac{n}{(n+1)^2}\left(x_{n+1}\ -\ \overline{x_n}\right)\left(y_{n+1}\ -\ \overline{y_n}\right)\ +\ \frac{n}{n+1}s_{xy}^n
\end{align}
これで漸化式の完成です。
#Pythonで実装
漸化式ができたので実際にPythonで実装しましょう。今回は「ベクトルが逐次的に与えられ、そのベクトル集合の分散共分散行列を求めたい」というモチベーションの下、実装を行います。
import numpy as np
def calc(next_val,times,var_cov_mat=None):
'''
計算を行う
'''
if times > 1:
# 分散共分散行列の更新
var_cov_mat = np.outer(next_val,n_mean)*(times/(times+1)**2) + var_cov_mat*times/(times+1)
else:
# 初期状態を定義、分散共分散行列=単位行列
var_cov_mat = np.identity(len(next_val))
return next_mean, var_cov_mat
これで完成。あとはデータをどんどん入れていけば分散共分散行列を逐次的に得ることができます。
#検証
今回は512次元のベクトルを使います。ベクトルの各成分は0以上1未満の数値をランダムに与えました。
比較方法は上記の手法で求めた行列と、1回ずつnumpyで計算した行列の成分毎にみた平均二乗誤差の推移をみます。
結果はこちら。
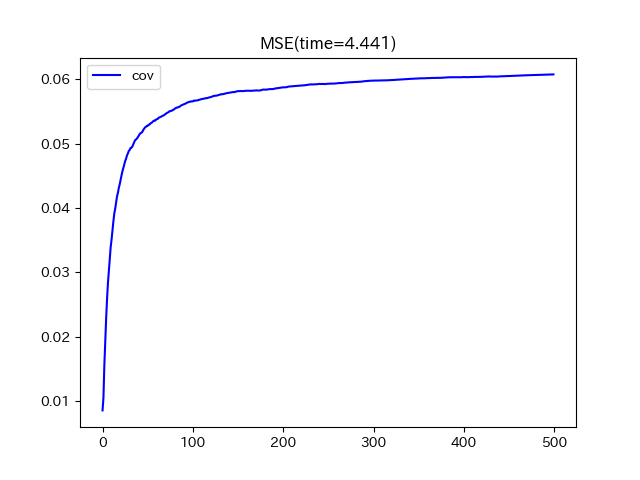
500回の計算を4秒ちょっとで行い、おおよそ0.06くらいまでに収まるように推移しています。
#まとめ
今回は共分散の逐次更新を可能にする共分散の漸化式を導出し、Pythonによる実装を行いました。計算結果はきれいに書けていると思いますが、「もっときれいに書けた!」という方がいらっしゃいましたらぜひ教えてください。
実装に関しては、初めの導入で書いた通り、相談を受けたところからスタートしており、受けた相談の内容を反映させる形で実装していますので、他の形で実装したいというときは前半の式の部分を使って実装していただければ良いと思います。
ここからは本筋とは関係ありませんが、この式変形は結構大変でした。もし、式変形に興味がありましたら、上述の部分で空いている穴を埋めてみるのも良いかもしれません。結構丁寧に埋めたつもりなので、埋める場所がないと思ったら初めから自力で計算してみても面白いかもしれません。
#参考にしたサイト
分散の逐次更新