量子多体系をシミュレートする
量子シミュレーションとは、量子多体系の振舞いを、制御可能な**"人工量子系"**を用いてシミュレートすることです。
量子多体系の物理
世の中には、様々な量子多体系が存在します。例えば、物性物理や量子化学においては、電子や原子といった量子が複雑な相互作用の下、どのような振舞いなのかが重要となります。しかし実は、量子多体系のダイナミクスをシミュレートするのは非常に難しいタスクなのです。量子多体系のシミュレーションがいかに難しいこかを想像していただくために、spin-1/2の粒子が$N$個並んだ量子系を考えてみましょう。
$$
\def\bra#1{\mathinner{\left\langle{#1}\right|}}
\def\ket#1{\mathinner{\left|{#1}\right\rangle}}
\def\braket#1#2{\mathinner{\left\langle{#1}\middle|#2\right\rangle}}
$$
それぞれの粒子は、$\ket{\uparrow}$と$\ket{\downarrow}$の二つの量子状態をとることができます。つまり、この粒子が$N$個並んだ時、この量子系を表現するためには、$2^N$個の確立振幅が必要になります。また、時間発展まで考えると$2^N\times 2^N$の大きさの行列が必要になります。このような量子多体系をコンピュータで表現する時に必要となるメモリ数は、例えば、数十程度の粒子数でさえ、スーパーコンピュータをもってしても、手に負えない領域になってしまいます。
このような問題に対して、ファインマンによって提案された解決策が、量子シミュレーションです。シミュレータ自体が、量子的なシステムなので、$N$個の量子ビットを扱うことで、指数関数的に情報が増えても、対応することが可能になるのです。量子系のダイナミクスを知りたければ、量子力学の原理で動作する計算機、つまり、量子シミュレータで計算せよということですね。
量子シミュレーションとは
さて、量子シミュレーションとは、ある量子系のダイナミクスを量子的なシミュレータを使って知るということです。具体的な問題設定から考えてみると、とある量子系の波動関数を$\ket{\psi}$として、ハミルトニアン$H$のもとで、どのように時間発展するのかを知りたいとします。
この時、時間$t$における量子状態は初期状態を$\ket{\psi(0)}$として、
$$\ket{\psi(t)}=e^{-iHt}\ket{\psi(0)}$$
と表現できます。この過程を量子的なシミュレータを用いてシミュレートすることが、まさしく量子シミュレーションなのです。
アナログ量子シミュレーションとデジタル量子シミュレーション
実は、量子シミュレーションには大きく分けて
- アナログ量子シミュレーション
- デジタル量子シミュレーション
の2つの種類が存在します。結論から申し上げると、その違いは量子系の時間発展のシミュレーションの仕方に違いがあります。
アナログ量子シミュレーションは、対象とする量子系のモデルを模倣した人工量子系を用意し、その時間発展を観測することで、系のダイナミクスに関する情報を得ます。つまり、対象とする量子系の初期状態$\ket{\psi(0)}$や、ハミルトニアン$H$を再現し、実際に時間発展させるのです。
一方で、デジタル量子シミュレーションは、対象とするハミルトニアン$H$によるユニタリ演算子$U$を複数の量子ゲートに分解し、それらを量子状態に作用させることで、時間発展を実現します。
アナログ量子シミュレーション
アナログ量子シミュレーションでは、単純に系のハミルトニアンの下で時間発展させ、得られる最終状態を観測するというものでした。実際には、何らかの制御可能な量子物理系を用いることで、シミュレーションを行います。
具体的な例として、横磁場イジングモデルを考えてみましょう。
$$H = -J\sum_{i=1}^{n}\sigma_z^i\sigma_z^{i+1}-h\sum_{i=1}^{n}\sigma_x^i$$
このハミルトニアンからもわかるように、
- スピンを表現する量子ビット
- スピン間相互作用
- 量子ビットの制御、観測、初期状態生成
- 局所磁場の制御
といった自由度が必要となります。これらを実現できるような量子物理系を用いることで、アナログ量子シミュレーションを実現するのです。これまで、超電導量子ビットや冷却原子系等でアナログ量子シミュレーションが実現されており、例えば、光格子中の冷却原子を用いたハバードモデルの量子シミュレーションや、冷却イオンを用いたイジングモデルの量子シミュレーションが代表的な例として挙げられます。
デジタル量子シミュレーション
デジタル量子シミュレーションでは、所望のユニタリ演算を、複数の量子ゲートで表現します。ここで、とあるユニタリ行列$U$を考えます。この時、ユニタリ行列に対応するハミルトニアン$H$が、以下のように局所的な相互作用を表すハミルトニアン$H_i$の和で記述されるとします。
$$H = \sum_{i=1}^NH_i$$
ここで、もし局所的な相互作用を表すハミルトニアン$H_i$が交換可能、つまり$[H_i, H_k]=0$であるならば、ユニタリ演算$U$は、以下のように記述できます。
$$U=e^{-iHt}=e^{-i\sum_{i=1}^NH_it}=e^{-iH_1t}e^{-iH_2t}\cdots e^{-iH_Nt}=\prod_{i=1}^{N} e^{-iH_it}$$
つまり、各項の$e^{-iH_it}$を量子ゲートで実装することができれば、このユニタリ演算が実現可能です。しかしながら、たいていの興味のあるハミルトニアンの場合は、非可換 $[H_i, H_k]\neq0$ となり、$e^{-iHt}\neq\prod_{i=1}^{N} e^{-iH_it}$となります。そのため、素直にこの演算を実装することはできません。
トロッターの公式
次なる作戦として、微小時間の時間発展にハミルトニアンを分解して、近似的にそのダイナミクスのシミュレーションを行うということが考えられます。そこで用いられるのが、トロッターの公式です。トロッターの公式とは、以下の式で与えられる公式です。
$$\lim_{n \to \infty} (e^{-iH_it/n}e^{-iH_kt/n})^n = e^{-i(H_i+H_k)t}$$
そして、このトロッターの公式と、指数関数のテイラー展開を用いることで、
$$e^{-i(H_i+H_k)\delta t}=e^{-iH_i\delta t}e^{-iH_k\delta t}+O({\delta t}^2)$$
という関係式を導くことができます。ただし、微小時間$\delta t=t/n$としています。そして、これを拡張することで、
$$e^{-i\sum_{i=1}^NH_i\delta t}=e^{-iH_1\delta t}e^{-iH_2\delta t}\cdots e^{-iH_N\delta t}+O({\delta t}^2)=\prod_{i=1}^{N} e^{-iH_i\delta t}+O({\delta t}^2)$$
となります。この式における各項の$e^{-iH_it}$を量子ゲートで実装することができれば、非可換なハミルトニアンの和からなるユニタリ演算もシミュレーションすることができます。当然ながら、$\delta t\rightarrow0$の極限で、$e^{-i\sum_{i=1}^NH_i\delta t}\approx\prod_{i=1}^{N} e^{-iH_i\delta t}$となることがわかります。つまり、正確にハミルトニアンを再現するには、微小時間をできるだけ小さく設定することが必要なわけです。
イジングモデルを例にして
デジタル量子シミュレーションの具体例として、横地場イジングモデルを考えてみましょう。
イジングモデルの数値計算
先ず、マスター方程式による数値計算で、イジングモデルにおけるダイナミクスを見ていきます。今回は、QuTiPを使用しました。また、周期境界条件$\sigma_z^{n+1}=\sigma_z^1$を仮定しています。
モジュールのインポート
from qutip import *
import numpy as np
import matplotlib.pyplot as plt
演算子やパラメータの設定
# スピンの数
N_spin = 5
# 恒等演算子
I = qeye(2)
# パウリ演算子
sx = sigmax()
sz = sigmaz()
# スピンの状態
s_up = basis(2, 0)
s_down = basis(2, 1)
初期状態生成
$$\ket{\psi(0)} = \ket{\uparrow\uparrow\cdots\uparrow}$$
ini_list = []
for i in range(N_spin):
ini_list.append(s_up)
psi0 = tensor(ini_list)
ハミルトニアン
$$H = -J\sum_{i=1}^{n}\sigma_z^i\sigma_z^{i+1}-h\sum_{i=1}^{n}\sigma_x^i$$
Hzz = 0
Jz = -2*np.pi*1
for i in range(N_spin):
i_list = [I]*N_spin
i_list[i%N_spin] = sz
i_list[(i+1)%N_spin] = sz
Hzz += Jz*tensor(i_list)
Hx = 0
h = 3*Jz
for i in range(N_spin):
i_list = [I]*N_spin
i_list[i] = sx
Hx += h*tensor(i_list)
H = Hzz+Hx
オブザーバブル
obs_local = []
obs = 0
for i in range(N_spin):
local = [I]*N_spin
local[i] = sz
obs_local.append(tensor(local))
obs += tensor(local)/N_spin
量子ダイナミクスの計算
tim = 0.5 # 時間発展の時間
step = 100
t_list = np.linspace(0, tim, step)
# master equation
result = mesolve(H, psi0, t_list, [], [])
# 期待値計算
mag = expect(obs, result.states)
グラフにプロット
plt.plot(t_list, mag, color = 'b')
plt.xlabel('Time', fontsize=20)
plt.ylabel(r'$\langle\sigma_z\rangle$', fontsize=20)
plt.xlim(-0.01,t_list[-1]+0.01)
plt.ylim(-1.0,1.05)
plt.xticks([0, 0.1, 0.2, 0.3, 0.4, 0.5], fontsize=15)
plt.yticks([-1, 0, 1], fontsize=15)
plt.show()
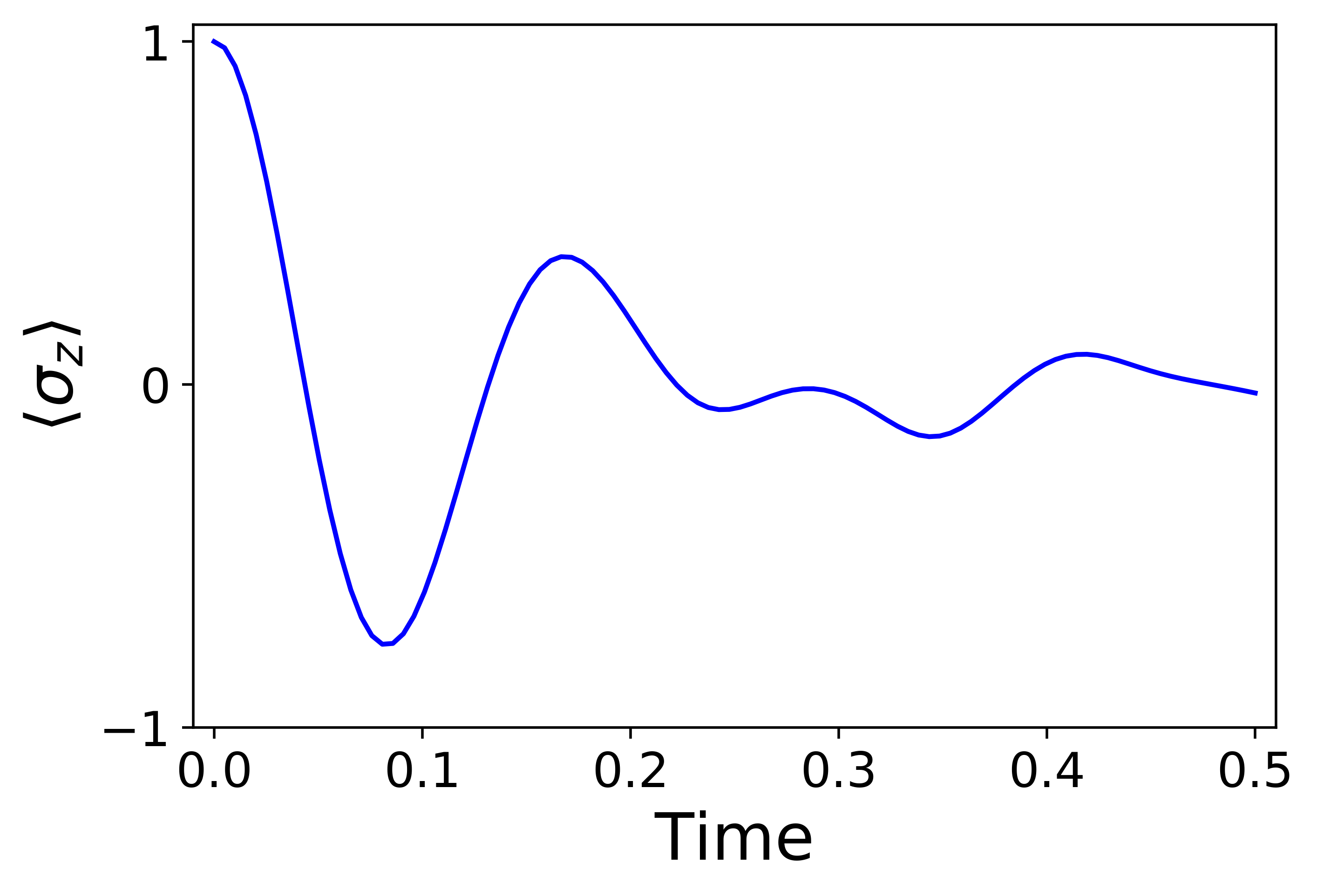
トロッター分解を用いたイジングモデルのシミュレーション
それでは、トロッター公式を用いて、横地場イジングモデルのハミルトニアンを実現する方法を考えてみます。ここで、ハミルトニアンを
$$H = -J\sum_{i=1}^{n}\sigma_z^i\sigma_z^{i+1}-h\sum_{i=1}^{n}\sigma_x^i=H_{zz}+H_x$$
のように書き直します。つまり、トロッターの公式から、微小時間$\delta t$の間における時間発展を表す演算子は、
$$U_{Ising}^{\delta}\approx e^{-iH_{zz}\delta t}e^{-iH_{x}\delta t}$$
となります。$e^{-iH_{x}\delta t}$に関しては、
$$e^{-iX_1\delta t}e^{-iX_2\delta t}\cdots e^{-iX_i\delta t}=\prod_{i=1}^{N} e^{-iX_i\delta t}$$
となります。つまり、回転ゲート
$$R_x(\delta\theta)=e^{-i\frac{\delta\theta}{2}X}$$
を作用させるということになります。
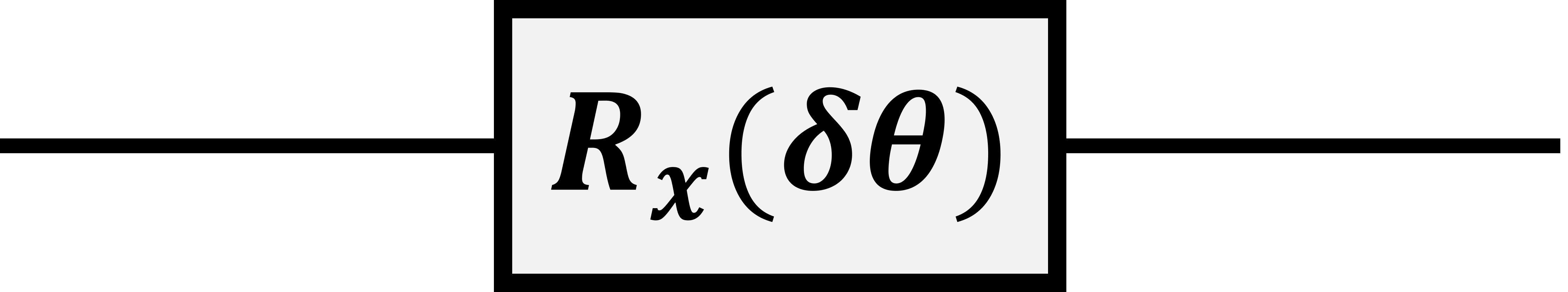
ただし、$\delta\theta=h\delta t$となっています。
次に、スピン間相互作用を表す$e^{-iH_{zz}\delta t}$に関して考えてみましょう。こちらは、結論から答えると、以下のような量子回路で実現されます。

この量子回路が本当に、スピン間の相互作用を表しているのかは、以下のように確認することができます。
U = U_{\rm CNOT} I\otimes R_{z}(\theta) U_{\rm CNOT} = \begin{pmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1 \\
0 & 0 & 1 & 0
\end{pmatrix}\begin{pmatrix}
e^{-i\theta/2} & 0 & 0 & 0 \\
0 & e^{i\theta/2} & 0 & 0 \\
0 & 0 & e^{-i\theta/2} & 0 \\
0 & 0 & 0 & e^{i\theta/2}
\end{pmatrix}\begin{pmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1 \\
0 & 0 & 1 & 0
\end{pmatrix}
= \begin{pmatrix}
e^{-i\theta/2} & 0 & 0 & 0 \\
0 & e^{i\theta/2} & 0 & 0 \\
0 & 0 & e^{i\theta/2} & 0 \\
0 & 0 & 0 & e^{-i\theta/2}
\end{pmatrix}
これは、
R_{zz}(\theta) =exp(-i\frac{\theta}{2}Z\otimes Z) = \cos(\frac{\theta}{2})I\otimes I-i\sin(\frac{\theta}{2})Z\otimes Z
= \begin{pmatrix}
e^{-i\theta/2} & 0 & 0 & 0 \\
0 & e^{i\theta/2} & 0 & 0 \\
0 & 0 & e^{i\theta/2} & 0 \\
0 & 0 & 0 & e^{-i\theta/2}
\end{pmatrix}
と等しくなることがわかります。
Qiskitでの実装
モジュールのインポート
import numpy as np
from qiskit import QuantumCircuit, Aer
from qiskit.opflow import I, Z
from qiskit.quantum_info import Statevector
import matplotlib.pyplot as plt
演算子やパラメータの設定
# スピン数
N_spin = 5
# 時間発展にかかる時間
t = 0.5
# 分割数
n = 300
# 時間のステップ
dt = t/n
# パラメータ設定
J = -1 * 2 * np.pi
h = 3 * J
オブザーバブル
# 下準備
obs_prep = []
for i in range(N_spin):
pauli = []
for k in range(N_spin):
if k == i:
pauli.append(Z)
else:
pauli.append(I)
obs_prep.append(pauli)
# オブザーバブル
mag_obs = [obs_prep[i][0] for i in range(N_spin)]
obs = 0
for i in range(N_spin):
for k in range(N_spin-1):
mag_obs[i] = mag_obs[i].tensor(obs_prep[i][k+1])
obs += mag_obs[i]/N_spin
量子回路の実装
tim = np.linspace(0, t, n)
pop = []
backend = Aer.get_backend('statevector_simulator')
for i in range(n):
qc = QuantumCircuit(N_spin)
for j in range(i):
for k in range(N_spin):
# ZZ term
qc.cx(k, (k+1)%N_spin)
qc.rz(2*dt*J, (k+1)%N_spin)
qc.cx(k, (k+1)%N_spin)
# x term
qc.rx(2*dt*h, k)
job = backend.run(qc, shots = 1024)
result = job.result()
q_state = Statevector(result.get_statevector())
pop.append(np.real(q_state.expectation_value(obs)))
if i%100 == 0:
print(i)
グラフにプロット
plt.plot(tim, pop, color = 'r')
plt.xlabel('Time', fontsize=20)
plt.ylabel(r'$\langle\sigma_z\rangle$', fontsize=20)
plt.xlim(-0.01,tim[-1]+0.01)
plt.ylim(-1.0,1.05)
plt.xticks([0, 0.1, 0.2, 0.3, 0.4, 0.5], fontsize=15)
plt.yticks([-1, 0, 1], fontsize=15)
plt.show()
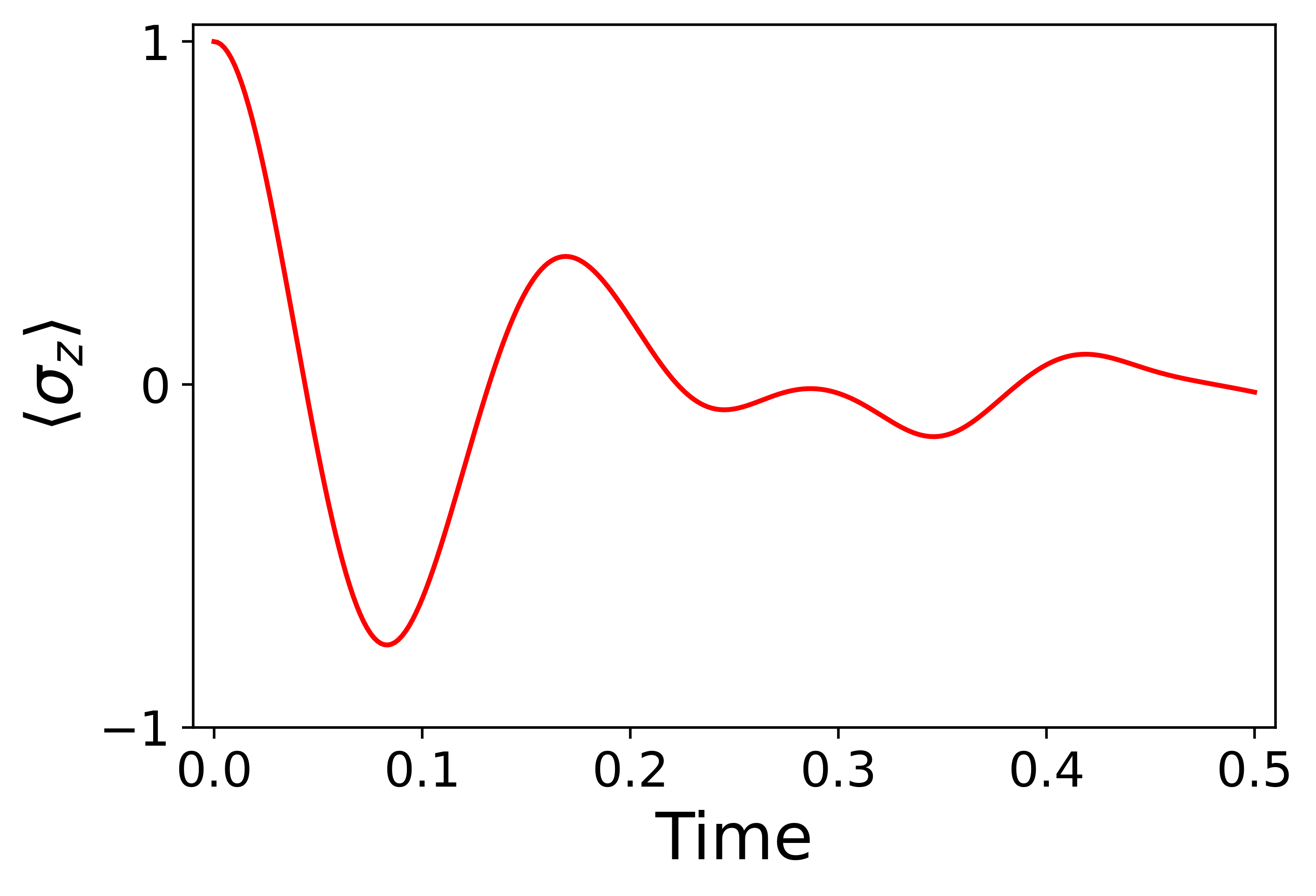
参考
(1): I. M. Georgescu, S. Ashhab, and F. Nori, Rev. Mod. Phys. 86, 153 (2014).
(2): トロッター分解を用いた量子シミュレーション

