IPFactory Advent Calender 2019 5日目
5日目も書かせていただきます。
IPFactory所属、ISC 1年のpycysです。
下記のアルゴリズムでは、解く過程で仮置きを必要とする問題は解けないため、
参考にする際は気をつけてください。
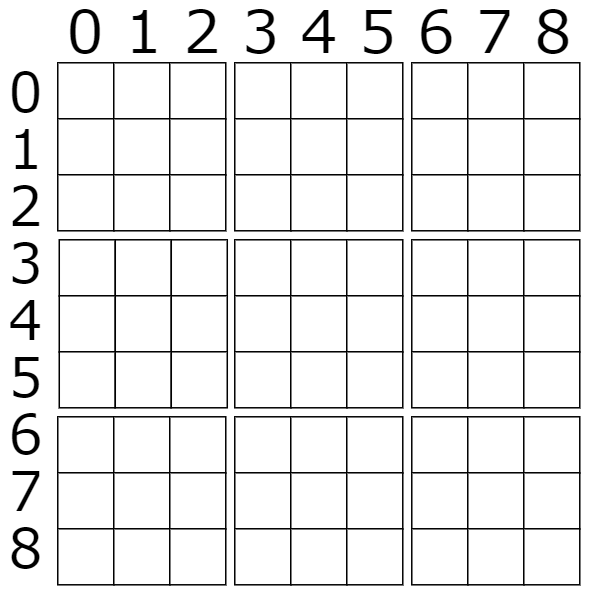
プログラムが受け取るデータ
※画像の数字は添字であり、受け取るデータではありません
0から9までのいずれかの数字81個が空白区切りで渡されるものとします。
ナンプレの左上マス(0, 0)の値は1番目に、右上マス(0, 8)の値は9番目に、
左下マス(8, 0)の値は73番目に、右下マス(8, 8)の値は81番目に記述されています。
0は空白を、1から9はその数字が設定されていることを示します。
どう解いていくか
ある数字が入る可能性のあるマスをどんどん削って少しずつ位置を確定させていきます。
- 下記のいずれかの条件を満たした場合、ある数字nの位置が確定します。
- ある3×3枠内でnを置ける場所が1マスのみ
- ある縦列内でnを置ける場所が1マスのみ
- ある横列内でnを置ける場所が1マスのみ
- あるマスに置ける数字がnのみ
ではnを置けるか置けないかの判断をするために、置ける数字を調べる処理が必要になりますね。
3次元配列内に置ける数字をまとめて入れるのが一番わかりやすそうです。
あるマスに置けない数字を削っていくので、最初に1から9までの数字を全部入れます。
3次元配列に数字を入れた後、既に位置が確定している数字を参照し、
同3×3枠内、同縦列、同横列からその数字を削ります。
上記の処理を終えたら、上で挙げた確定条件を満たしたマスがないか確認し、
条件を満たしたマスがあった場合は、参照用の2次元配列に反映後、未確定数字参照用の3次元配列から数字を削ります。
あとはチェックして反映して削っての繰り替えしで解けま...せん。
普通に解けない例外を弾く
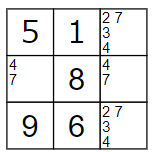
例外1
中段の両端に4と7が、右の縦列の上下に2と3が入ることは確定しているのに、
余分な4と7があるため、状況次第ではうまく処理できなくなるかもしれません。
これは3×3マスのみならず、縦列、横列でも起こりうる事です。
上の画像を例にして、これを回避するための処理を説明します。
まず数字未確定配列の各3×3枠内で、1から9までの値のインデックスをそれぞれ収集し、
その中で、同じインデックスを持つ数字を割り出し、割り出した数字の数と、
掛け持ちしているインデックスの数が一致した場合、その内にある他の邪魔な数字を排除します。
例外2
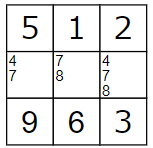
画像は似ていますが、さっきの話と地続きの内容ではないので注意してください。
仮にこんな3×3枠があったとします。
マズい、大変マズいですね。
中段に4,7,8が入るため、本来ならばこの3×3枠を除く同横列の未確定マスから4,7,8を弾く必要がありますが、
この3つの数字は位置が確定していないため、その処理が行われません。
ということで、ある3×3枠のある列にある数字が入ることが確定した際に、枠外の同列各マスに存在するであろう数字候補を削ります。
まず、3×3枠の横列にあたる未確定数字マスを1列ずつset()で集合にし、
その3つの集合で排他的論理和集合を作れば、中に入っているのはいずれかの横列に入ることが確定している数字です。
あとはその数字がある列を特定して、枠外同列の未確定数字マス内にある列確定数字を排除します。
縦列も同様です。
ここまでをいくらか繰り返します。
計算量すごそう...(小並感)
こんな感じでやっていけば解けると思います 多分。
最後に
最後まで読んでいただきありがとうございます。
何が書いてあるのかわからなければ、理解するのを諦めてください。
私も何を書いているのかよくわからないです。
後編の方にコード載せますが、一応GitHubの方にも載せておきます。
コードはここです。