はじめに
昨今、大量のデータ種から特定のデータ種に関わりの強いデータ種のみを抽出するような解析を求められたりします。
こういう状況の時にスパース性に基づく推定を行うことが有効な場合があります。
このスパース推定は、基本的なライブラリはRやpythonにもありますので試す事自体は難しくありません。
ということで、このスパース推定の初歩のところ(Lasso, L1正則化によってスパース化された線形回帰とその使い方)をアドカレの機会にまとめてみたいと思います。
Lassoとは
L1正則化によってスパース化された線形回帰をLassoと呼びます。ベースは次の線形回帰の式です。
y=\beta_1x_1 + ... + \beta_px_n + \epsilon
手持ちのデータ(x,y)から各βを算出してモデルを作成するのですが、xの変数が非常に多いがデータ点数が少ない場合は、各βを算出することが数理的にできません。
この場合、「目的変数に関与するのは僅かな説明変数のみ(スパース性という)」という仮定を置くことで、絞り込んだ目的変数についてのβを算出することができます。
これを解くための統計理論を**Lasso(L1正則化)**と言います。
Lassoおいて嬉しい点を箇条書きでまとめると、次の2点になります。
- データレコード数よりデータ種類数(変数)が多い場合(p>n)でも、解くことができる
- 変数の絞り込みや係数の重みより、重要なデータの種類が何かが直感的に理解可能である
この2点が、次のような状況を解決してくれる事が期待できます。
- データの種類はたくさんあるがデータ点数は十分にない。その場合でも解析できる。
- 多くのデータ種の中から、予測において重要なデータ種のみを知る事ができる
これらは実応用上、大変嬉しい事のように思います。
なので、現在も派生の手法が研究され続けられていると理解しています。
文章の説明に終始してしましたが、数理の説明は勉強中の私には荷が重いので、「岩波データサイエンスvol5」か「スパース推定法による統計モデリング 」を
ご確認頂ければと思います。
ちなみに、p>nの状況だがスパース性を仮定せず解く方法もあり、これをRidge(L2正則化)と呼びます。
また、L1とL2の両方を任意のバランスで混ぜたものをElasticNetと呼びます。
このバランスは各種ライブラリで設定されているαというパラメータで調整する事ができ、下記で紹介したライブラリでもαを設定する事ができます。
RでLassoを実施するためのライブラリ
glmnet
一番メジャーなライブラリですので、まずはこちらの使用を検討するのが良いと思います。
glmnetのイントロダクションを参考にして、タイトルの目的にそった最低限の使い方となる基本的な線形回帰を基にしたスパース推定を行います。
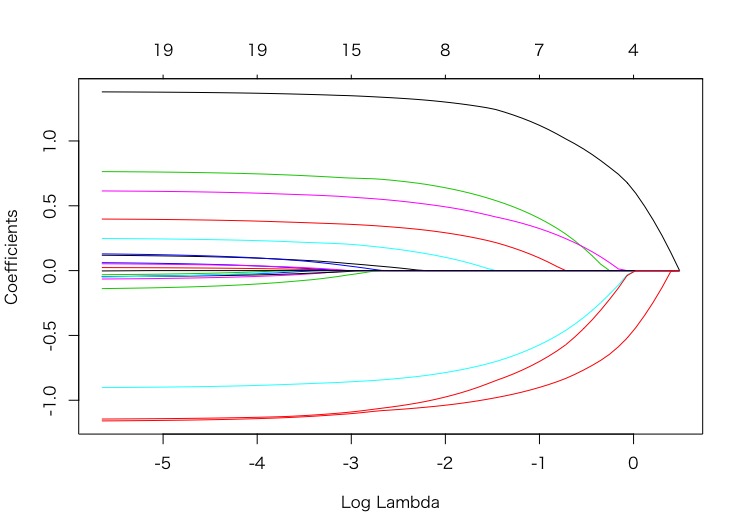
解パスの生成
λという変数の削減度を強めるパラメータがあるのですが、この値を推移した際に、変数の個数や各変数の大きさがどの程度変動していくかを示した図を生成することができます。
library(glmnet)
data(QuickStartExample)
fit <- glmnet(x,y) # このxはMatrix型である必要がある点に注意すること
plot(fit) #解パス作成
この図ですが、色ごとに各係数の値の推移を示しています。
x軸はL1正則化の強さ(λの大きさ)を表しており、
またy軸は各係数の大きさを表しています。なお、各xは標準化(平均0、標準偏差1となるように変換)が自動でされているので、データの大小等を気にせずに、係数の大小を比較することができます。
左に行くほどλ値が小さくなっているので、スパース性が弱くなり変数が多くなっていることが分かります。
解パスはこのようにλを推移した際に、各係数値がどう変わるかを可視化する図なので、変な推移になっていないかを確認してみるのが良いと思います。
(例:ある変数が出現したら、今まで係数値が高かった別の変数が0に落ちてしまったなど。)
λをクロスバリデーション(CV)で決定
先ほどの解パスでお好みの説明変数の数にするように決め打ちでλを指定する方法もありますが、CVで最もエラーの小さいλを計算して決める方が、多くの場合において最良に思います。
CVを実行するための関数もglmnetには用意されています。(ちなみに、このCVはデータ数が増えると処理時間が掛かりがちになりますが、
並列で処理することも可能です。こちらのような事前の対応が必要なので、ご確認ください。)
なお、CVは経験的にfold数を10か5で行うのが良いとされています。デフォルトでは10なので、そのままにするのが無難なのかなと思います。
CVで得られたlambda値はlambda.minを指定することで簡単に得られることができます。
また、これよりも少し誤差を犠牲にしつつスパース性を上げたい場合はlambda.1seを使うこともできます。決め打ちでlambda値を決めるのと併せて、状況に応じて使い分けてください。
cv.fit <- cv.glmnet(x,y) #CrossValidationの実施
cv.fit$lambda.min #CrossValidationで得られた最良のlambda値
[1] 0.07569327
決定したλを適用してモデルを作成し、係数を確認する。
CVで決定したλを適用し、L1正則化での線形回帰モデルを作成します。その後coef関数を使って変数を確認します。
fit <- glmnet(x, y, lambda=cv.fit$lambda.min)
coef(fit) #係数の一覧が表示される
s0
(Intercept) 0.14867809
V1 1.33376362
V2 .
V3 0.69787555
V4 .
V5 -0.83726103
V6 0.54334630
V7 0.02668587
V8 0.33740506
V9 .
V10 .
V11 0.17105939
V12 .
V13 .
V14 -1.07553017
V15 .
V16 .
V17 .
V18 .
V19 .
V20 -1.05279163
.と記載された変数は除外された変数になります。
また、各変数は正則化されているので、係数値の大小等から目的変数の寄与度を確認することが可能になっています。
今回の場合、20種類の目的変数があったのが、9個まで候補が絞られ、かつ、正の関係が1番目の変数(V1)に、負の強い関係が20番目の変数(V20)にある事が推定されました。
このように見る事で、データの関連度について候補を絞ることと関係性の大小を同時に推定する事ができます。
biglasso
glmnetはデータを全てメモリ上に抱えてしまうので、巨大データを扱う時にそこそこのメモリを消費してしまいます。
これを避けるためにbigmemoryというファイルベースで処理可能にしたライブラリがbiglassoです。
ただし、ファイルベース処理なので、あまりにデータが大きいと処理時間が増大してしまうことに注意が必要です。
また、glmnetに比べてできることが少し限られることにも注意が必要です。
しかし、今回の内容程度ならbiglassoでも可能です。
biglasso tutorialを参考に、先と同じようなことをやってみます。
余談ですが、MacOSでcv.biglassoを行うときはXQuartzを入れないとエラーが出て動かないのでお気をつけください。
library(glmnet) #下記のデータを使うためだけに読んでいます。
data(QuickStartExample)
library(biglasso)
x.bm <- as.big.matrix(x) #目的変数はbigmatrixに変換する必要があります。
fit <- bigmatrix(x.bm, y)
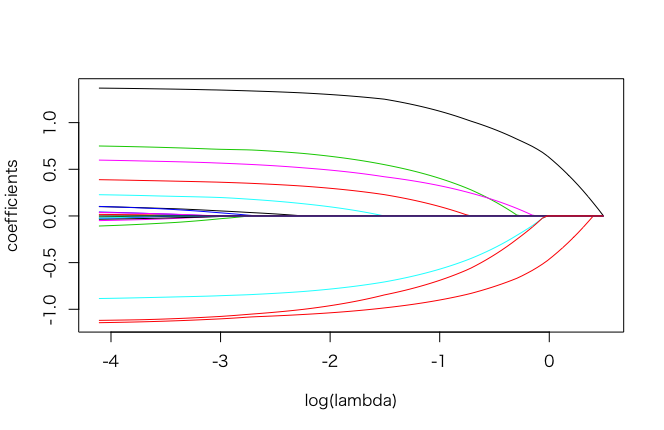
plot(fit) #解パス図の作成
cv.fit <- cv.biglasso(x.bm, y) #MacOSではXQuartzが必要になります。
fit <- biglasso(x.bm, y, lambda=cv.fit$lambda.min)
coef(fit)
21 x 1 sparse Matrix of class "dgCMatrix"
0.0812
(Intercept) 0.14916970
V1 1.33086063
V2 .
V3 0.69275131
V4 .
V5 -0.83280722
V6 0.53839024
V7 0.02175719
V8 0.33337199
V9 .
V10 .
V11 0.16460599
V12 .
V13 .
V14 -1.07202722
V15 .
V16 .
V17 .
V18 .
V19 .
V20 -1.04581782
HMlasso
最近、東芝と統計数理研究所よりHMLassoという、欠測値が入っていても推定処理可能という手法が発表されました。論文はこちらです。
今の範囲であれば、使う事自体は同じようにできますので、決め打ちで欠測値を入れてみて、試してみます。
まずは、欠測値があるデータではglmnetが使えないことを見てみます。
library(glmnet)
data(QuickStartExample)
x.na <- x
x.na[1,1] <- NA #決め打ちで欠測値を入れてみました。
fit <- glmnet(x.na, y)
結果は次のようになり、欠測値があるデータでは次のようにワークしません。
elnet(x, is.sparse, ix, jx, y, weights, offset, type.gaussian, でエラー:
外部関数の呼び出し (引数 5) 中に NA/NaN/Inf があります
しかし、hmlassoだとワークします。
library(glmnet) #先と同様下記のデータを使うためだけに読んでいます。
data(QuickStartExample)
x.na <- x
x.na[1,1] <- NA #決め打ちで1箇所だけ欠測値を入れてみます。
fit <- hmlasso(x.na, y) #xに[1,1]に欠測値があるデータを入れました。
plot(fit)
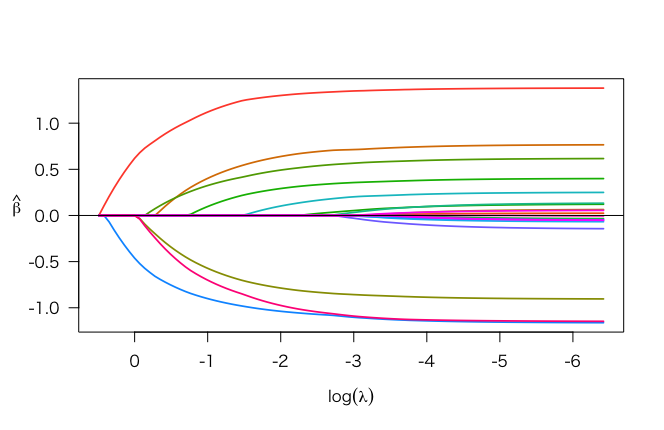
次のように解パス図が出ました。1つだけですが欠測値を入れたにも関わらず、今まで生成された図と同様のものが得られました。
当然、CV等も可能です。
cv.fit <- cv.hmlasso(x.na, y)
fit <- hmlasso(x.na, y, lambda=cv.fit$lambda.min)
fit$beta
推定された係数値も次のように確認する事ができます。(ちなみに、他のようにcoef(fit)ではNULLと表示され結果が見れません。ご注意ください)
[,1]
[1,] 1.33192790
[2,] 0.00000000
[3,] 0.69431415
[4,] 0.00000000
[5,] -0.83076759
[6,] 0.53916508
[7,] 0.02373921
[8,] 0.33890883
[9,] 0.00000000
[10,] 0.00000000
[11,] 0.16169273
[12,] 0.00000000
[13,] 0.00000000
[14,] -1.07239466
[15,] 0.00000000
[16,] 0.00000000
[17,] 0.00000000
[18,] 0.00000000
[19,] 0.00000000
[20,] -1.03393333
という事で、欠測値があっても同じような結果が得られる事を確認できました。
ただ、hmlassoライブラリは、研究発表からまだ時間が経っていない事から、未実装の機能もあり発展途上のライブラリと思いますので、その点は注意が必要と思います。
最後に
今回、スパース推定のうち、線形回帰におけるL1正則化(Lasso)についてのみ書きました。
実用上においても大変便利なのですが、欠点もあります。
例えば、「相関の強い説明変数が別にある場合、どちらか一方しか抽出してくれない」、
「そもそも線形回帰がベースなので、非線形の関係がある説明変数は抽出できない」、などでしょうか。
なので、改善手法も既に多く存在し、また現在も研究が盛んな分野です。
今後も改善手法等を継続的に調べていければ、と思います。
実行環境
- MacOS Mojave ver. 10.14.6
- XQuartz 2.7.11
- R version 3.6.1
- RStudio Version 1.2.5019
- glmnet 3.0-1
- biglasso 1.3-7
- bigmemory 4.5.33
- ncvreg 3.11-1
- hmlasso 0.0.1