短時間フーリエ変換を用いたスペクトログラムとPython実行方法の概要

はじめに

音などの波形データから特徴抽出や何らかの前処理の効果を確認するのに、短時間フーリエ変換を活用したスペクトログラム分析が有効な場合があります。scipy.signalなどのライブラリを使えば簡単にはできますが、個人的にわからない点も少なくなかったので、簡単ですがQiitaに書きます。

短時間フーリエ変換についての概要

まず、理論の理解は短時間フーリエ変換の基礎と応用, 日本音響学会誌 72 巻 12 号(2016) , pp.764–769」をメインに参考にさせていただきました。

まず、音声などの多くの音響信号は、複数の正弦波状の成分を含む周波数構造をもち時間と共に変化します。この様子を分解して確認するために、音響信号の時間周波数分析（特徴抽出、音源分析等でも）において、短時間フーリエ分析は古くから用いられた信号処理法の一つとのことです。

ということで、時間と共に変化する非周期信号において、一定時間の間隔で切り出し特定の短い区間での特徴的な正弦波を調べたいというときに短時間フーリエ変換が有効そうです。

この処理イメージとして先の論文の図1を引用させて頂きます。

※「短時間フーリエ変換の基礎と応用, 日本音響学会誌 72 巻 12 号(2016) , pp.764–769」のP765の図1より引用

窓関数

ここで、切り出し処理にあたる窓関数の選択も重要になりそうです。
窓関数は、特定区間のみ有効な数値を残してそれ以外を0にし、さらに並べたときに連続性や周期性も担保する関数ということです。
Wikipedia 窓関数によると、「周波数分解能」と「ダイナミックレンジ」の性能はトレードオフになるので、その辺を見極めての窓関数選択という感じになりそうです。
ハン窓とハミング窓がよく使われるようです。
また、Pythonで学ぶ音源分離（機械学習実践シリーズ）戸上真人 著によると、音響分析では特段の理由のない限り、ハン窓で問題ないようなことも書いてあることから、この辺りをまずは使ってみるのが良さそうです。

Pythonでの実装

Pythonでスペクトル解析【音声認識実践その1】を見させて頂くと、numpy.fftとnumpyの各窓関数を活用しての実装する方法もあるようですが、scipy.signal.spectrogramだと、より簡単に実行ができるようです。なので、こちらを使ってみます。
ひとまずscipy.signal.spectrogram公式ガイドのものをやってみます。

個人的な注意点

公式ページのサンプルコードの通りに、別途所有しているデータで可視化する際に少しハマった点としては、強度のdBの扱いです。
stack overflow, Wrong spectrogram when using scipy.signal.spectrogramの質問の回答そのものなのですが、spectrogram関数の出力値をpcolormesh関数で描画したい場合、次のように強度を加工する必要があります。(Wikipedia(英語)のDecibelのPower quantitiesも参照のこと)

plt.pcolormesh(times, frequencies, 10*np.log10(spectrogram))

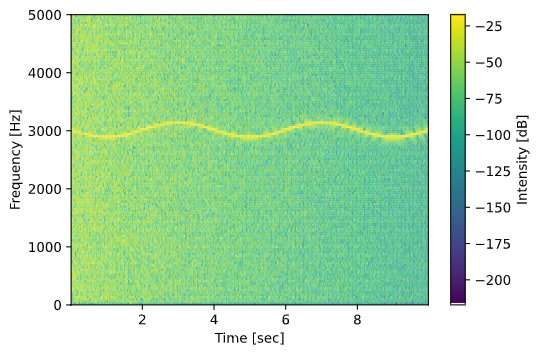
上記に加え、実行上の都合より修正を加えたサンプルコードとその結果を下に示します。

import numpy as np
from scipy import signal
import matplotlib.pyplot as plt

#波形データの作成
fs = 10e3
N = 1e5
amp = 2 * np.sqrt(2)
noise_power = 0.01 * fs / 2
time = np.arange(N) / float(fs)
mod = 500*np.cos(2*np.pi*0.25*time)
carrier = amp * np.sin(2*np.pi*3e3*time + mod)
noise = np.random.normal(scale=np.sqrt(noise_power), size=time.shape)
noise *= np.exp(-time/5)
x = carrier + noise

#スペクトログラム分析の実施
f, t, Sxx = signal.spectrogram(x, fs)

#図の描画
plt.pcolormesh(t, f, 10*np.log(Sxx)) #intensityを修正
plt.ylabel('Frequency [Hz]')
plt.xlabel('Time [sec]')
cbar = plt.colorbar() #カラーバー表示のため追加
cbar.ax.set_ylabel("Intensity [dB]") #カラーバーの名称表示のため追加
plt.show()

実行すると次のように図が出力されます。

なお、Pythonで学ぶ音源分離（機械学習実践シリーズ）戸上真人 著によれば、このスペクトログラムの書き方はnumpy.stftで短時間フーリエ変換をして、matplotlib.pyplot.specgramで描画するという方法もあるようなので、その辺はお好みで。

おわりに

スペクトログラムより、時間ごとの波形特徴がわかり、また2つの図を並べた際にどこに違いがあるかが分かるようになるので、有用な可視化手段と思います。
また、これに限らずですが、scipyライブラリなどが非常に整理されているので、手軽に実行できる一方で、意味のある可視化や分析をするには、裏側の理論や関数の内容の理解は欠かせないなと改めて実感しました。。

参考文献

• 短時間フーリエ変換の基礎と応用, 日本音響学会誌 72 巻 12 号(2016) , pp.764–769
• Discrete Fourier Transform(numpy.fft) — NumPy v1.20 Manual
• Window functions — NumPy v1.20 Manual
• scipy.signal.spectrogram — SciPy v1.6.0 Reference Guide
• Think DSP(Chap.3, Non-periodic signals, 3.4 Spectrogram)
• Pythonでスペクトル解析【音声認識実践その1】
• stack overflow, Wrong spectrogram when using scipy.signal.spectrogram
• Pythonで学ぶ音源分離（機械学習実践シリーズ）戸上真人 著
• Wikipedia, Power quantities(Decibel)

実行環境

• macOS Catalina 10.15.7
• VSCode 1.53.2
• Python 3.9.1
• numpy 1.20.1
• scipy 1.6.1
• jupyter 1.0.0
• matplotlib 3.3.4