はじめに
2つのデータの関係性を大まかに見るために、相関係数を計算することがある。
ここで、よく使われそうな3つの相関係数を簡単にまとめ、人工データで試して使い所を確認してみた。
#ピアソンの相関係数
2つの変数について線形関係を見るのに使われる。偏差の正規分布を仮定するパラメトリックな方法である。-1から1の値を取る。
r_{xy} = \frac{\displaystyle \sum_{i = 1}^n (x_i - \overline{x})
(y_i - \overline{y})}{\sqrt{\displaystyle \sum_{i = 1}^n
(x_i - \overline{x})^2\displaystyle \sum_{i = 1}^n
(y_i - \overline{y})^2}}
スピアマンの順位相関係数
2つの変数間の単調関係を評価するのに使われる。各変数の順位の差を求める(下記式のd)。ピアソンとは違いノンパラメトリックな方法である。-1から1の値を取る。
r_s = 1 - \frac{6\displaystyle \sum_{i = 1}^n {d_i}^2}{n(n^2 - 1)}
MIC(Maximun Information Coefficient)
線形の関係だけでなく非線形の関係も捉えることができる相関係数として使われる。0から1の値を取る。logic of blue様のページの説明が詳しい。qiitaでは非線形の相関分析 MIC についてが詳しい。
色々なデータの関係を作り、Rで計算してみる
RでMICを使うにはminervaパッケージが必要。
線形
下図の線形関係のデータを作って、各相関係数を計算する。
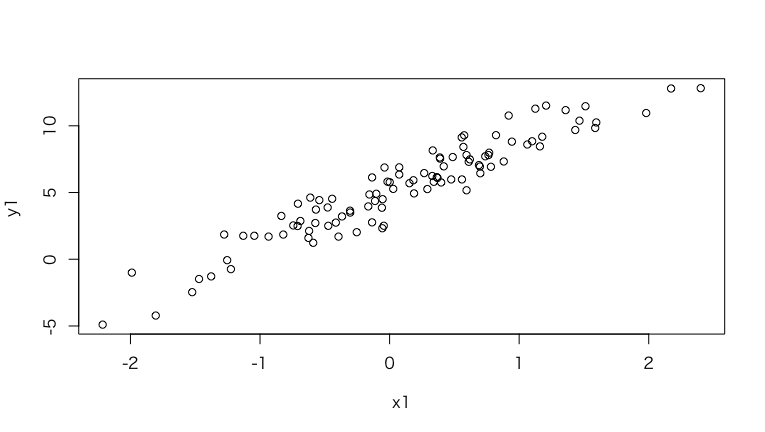
次のように、いずれでも高い数値を得ることができる。
> library(minerva)
> set.seed(1)
> x1 <- rnorm(n=100)
> set.seed(2)
> e <- rnorm(n=100)
> y1 <- 4*x1 + 5 + e
> plot(x1,y1)
> cor(x1, y1, method="pearson")
[1] 0.947994
> cor(x1, y1, method="spearman")
[1] 0.9432103
> mine(x1, y1)$MIC
[1] 0.8849022
3次曲線
この場合、ピアソンよりもスピアマンの方が数値が大きい場合がある。これは線形関係からは外れているものの、単調増加の傾向は強いためにこうなる。
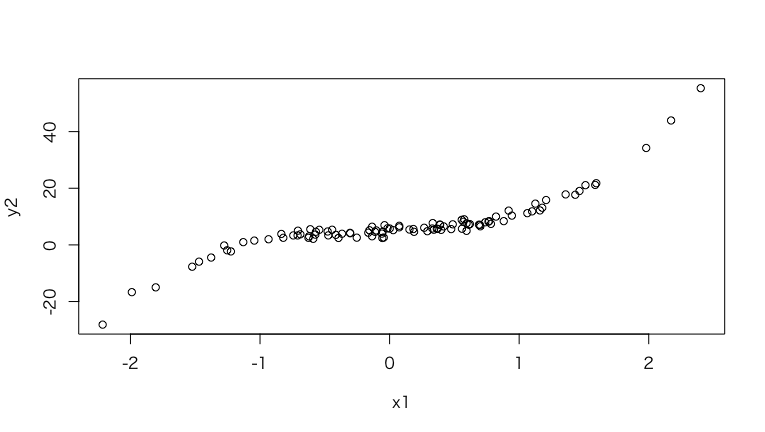
なおRのコードは、以降、先のものと続けて実行するものとする。
> y2 <- 3*x1^3 + x1^2 + 2*x1+ 5 + e
> plot(x1, y2)
> cor(x1, y2, method="pearson")
[1] 0.8569895
> cor(x1, y2, method="spearman")
[1] 0.9351695
> mine(x1, y2)$MIC
[1] 0.8290487
2次曲線
この場合、ピアソンもスピアマンも数値が絶対値的にかなり低くなるが、MICはきちんと高い数値が得られている。
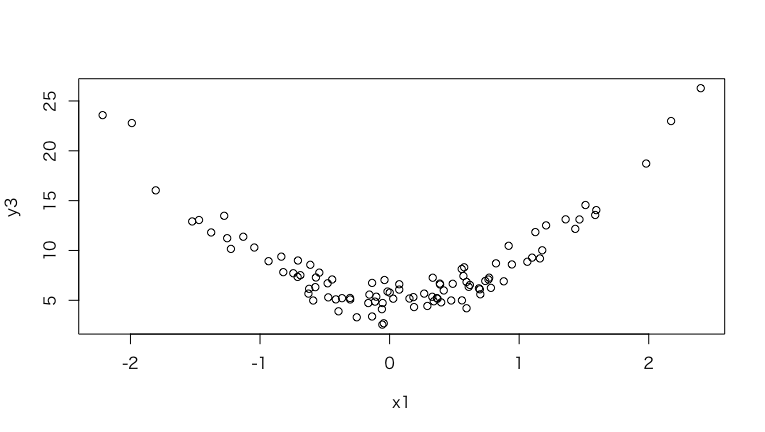
> y3 <- 4*x1^2 + 5 + e
> plot(x1, y3)
> cor(x1, y3, method="pearson")
[1] 0.08319834
> cor(x1, y3, method="spearman")
[1] 0.1007261
> mine(x1, y3)$MIC
[1] 0.7361249
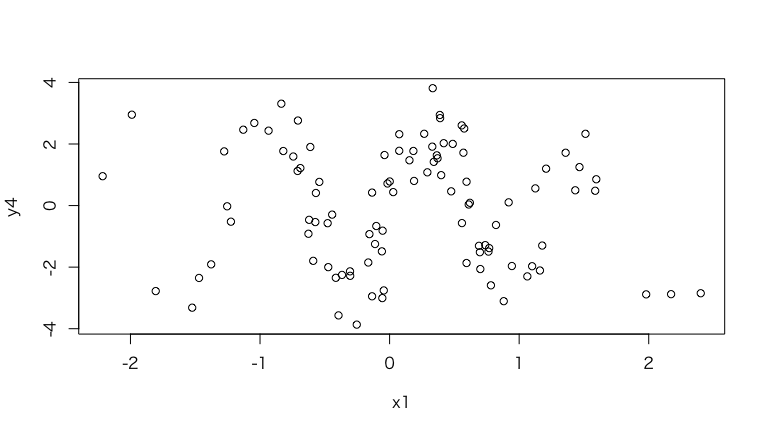
sinカーブ
> y4 <- 2*sin(5*x1) + e
> plot(x1, y4)
> cor(x1, y4, method="pearson")
[1] -0.0958496
> cor(x1, y4, method="spearman")
[1] -0.08838884
> mine(x1, y4)$MIC
[1] 0.638089
乱数関係
さすがにどれも絶対値的に低い値になる。しかし、MICは他のものよりは数値が高めに出るので、この点は気をつけた方が良いのかもしれない。
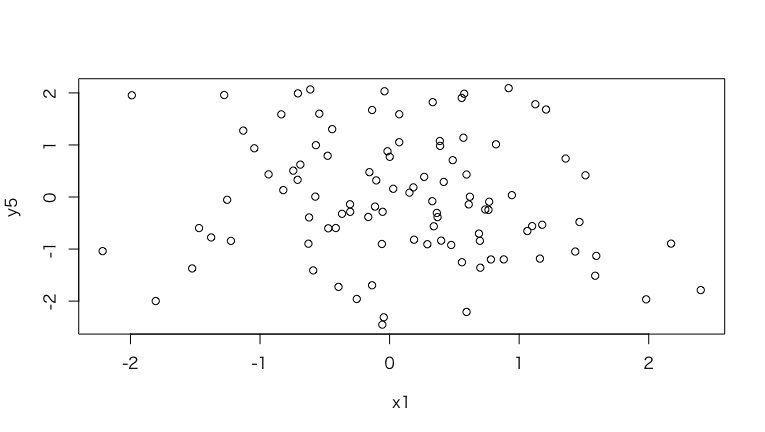
> set.seed(2)
> y5 <- rnorm(n=100)
> plot(x1, y5)
> cor(x1, y5, method="pearson")
[1] -0.1537208
> cor(x1, y5, method="spearman")
[1] -0.1537954
> mine(x1, y5)$MIC
[1] 0.2701778
最後に
ざっと3つの相関係数を色々な状況で使ってみた。データ種がたくさんあるときはこれらの指標を用いて関係性をざっと見てみたのち、有望なものは可視化し最終確認するのが良いと考える。