空間データの最も基本的な特性として空間相関(Spatial correlation)があります。本記事はこれに焦点を絞ってまとめてみます。
1. 空間相関のイメージ
「自分の場所とその近場は影響がある」と考える相関関係の考え方を導入したい。
例えば、正の相関(=自分が高い場合は近場も高い)のイメージとしては、大気汚染やウィルス感染など、汚染度や感染度が高い地域は周りも高いと解釈するような事象のイメージ。
また、負の相関(=自分が高い場合は近場は低い)のイメージとしては、売上が高いスーパーにある周りのスーパーは客を取られているので売上が低いなど、空間的な競争が生じているようなイメージ。
空間相関を見ることでこういったことをデータや可視化で把握することができる。
2. 近場をどう定義するか?
まず近場をどう定義するかが重要になる。2つの考えがある。
以下で説明するが、この辺はspdepパッケージのVignettesの一つの次が参考になる。
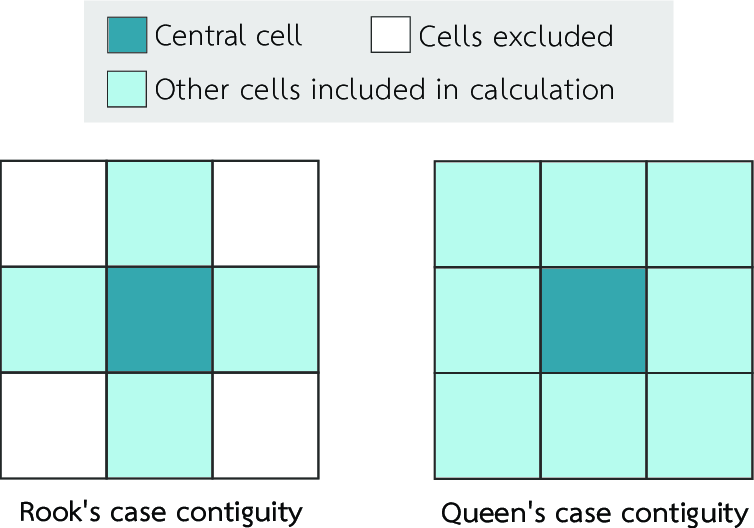
2-1. 隣接に基づく定義
隣り合った空間は近場と考える。よく使われるのが以下らしい。
- 上下左右を隣接とするルーク型隣接(Rook's case contiguity)
- 全方位を隣接とするクイーン隣接(Queen's case cotiguity)
2-2. 距離に基づく定義
距離に基づく方法で近場を定義する方法もある。この場合、距離減数関数を導入して、近接性を数値で得られるように定義する。詳しくは下記などを参照
3. 空間相関を見る統計量
「分析対象地域全域についてみる統計量」と「ゾーン(地点)ごとに地域差を見る統計量」がある。これらについてざっと見る。
3-1. モランI統計量
分析対象の全域で見る統計量の代表。
例えば日本国内において各都道府県の大気汚染度のデータを分析するなら、日本全体としてその大気汚染の具合は相関があるのか?ということを見るときに使う。
次のように計算する。Rではspdepライブラリで計算可能。
I = \frac{n}{\sum_{i=1}^n\sum_{j=1}^nw_{ij}}\frac{\sum_{i=1}^n\sum_{j=1}^nw_{ij}(x_i-\bar{x})(x_j-\bar{x})}{\sum_{i=1}^n(x_i-\bar{x})^2}
ここで、$n$は区間数(地点数)、$x_i$は区域iの属性値、$\bar{x}$は全区域の属性値の平均、$w_{ij}$は重み係数で隣接の定義に基づいて周辺とするエリアを1としそれ以外を0とする。
要は「自分自身と平均の差」×「隣接領域と平均の差」を全域分足して正規化して見る形になる。
この統計量はだいたい-1から1の間を取る。だいたいと書いたのは、じつは絶対値1を超えることがある。詳しくは下記「空間的自己相関に関するモランの修正型 I 統計量」参照のこと。
とはいえ、基本的には相関係数のように扱ってよく、正なら正の空間相関があるといえるし、負なら負の空間相関あるといえる。絶対値的には0.75あたりを超えるとまあ強いという感じ。
3-2. ローカルモランI統計量
区間ことに空間相関を評価したいことはよくある。
例えば日本国内において各都道府県の大気汚染度のデータを分析するなら、各都道府県ごとにその大気汚染の具合は周辺と相関があるのか?ということを見るときに使う。
次のように計算する。Rではspdepライブラリで計算可能。
I_i = \frac{(x_i - \bar{x})}{\sum_{k=1}^n(x_k - \bar{x})^2/(n-1)}\sum_{j=1}^nw_{ij}(x_j - \bar{x})
上記のように区間iごとに求めていく
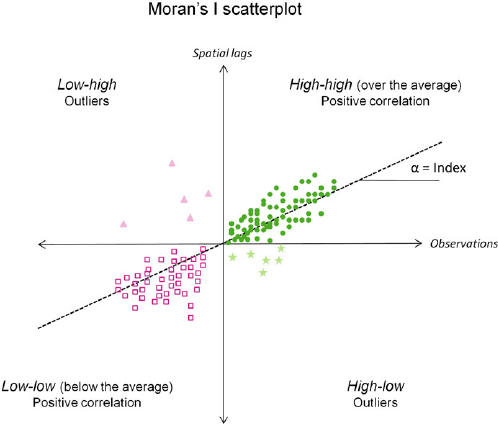
また、ローカルモランI統計量を散布図としてプロットすることで地域特性を可視化できる。次のように4つの領域に分けることができる
散布図の各領域の解釈は次:
- Iの絶対値が大きいケース
- High-high: ホットスポット(自分は強くて、周りも強い)
- Low-low: クールスポット(自分は弱くて、周りも弱い)
- Iの絶対値が小さいケース
- High-low: 一人勝ち(自分は強くて、周りは弱い)
- Low-high: 一人負け(自分は弱くて、周りは強い)
これをモラン散布図(Moran Scatterplot)と呼ぶ。
3-3. ギアリーC統計量とローカルギアリーC統計量
先のモランI統計量とローカルモランI統計量は、平均との差を活用していたため、局所的な傾向に対する感度が低い特性がある。
似たようなものにギアリーC統計量(Geary's C statistics)があるが、こちらは自分と周辺との差を活用するので、局所的な傾向に対する感度の高い特性を持つ。詳しくは下記の比較論文を参照のこと。
ギアリーC統計量は次のように計算する。Rではspdepライブラリで計算可能。
C = \frac{(n-1)}{2\sum_{i=1}^{n}\sum_{j=1}^{n}w_{ij}}\frac{\sum_{i=1}^{n}\sum_{j=1}^{n}w_{ij}(x_i - x_j)^2}{\sum_{i=1}^{n}(x_i - \bar{x})^2}
また、ローカルギアリーC統計量は次のように計算する。Rではspdepライブラリで計算可能。
C_i = \sum_{j=1}^nw_{ij}(y_i-y_j)^2
他にも似たような統計量はあるようだがこの辺で。。
4. データ形式など
今までリンクを紹介した通り、全てspdepパッケージを使う。
読み込むデータはshpファイルという図形情報と属性情報をもった地図データファイルを使えば良い。
openfileもググれば下記のように出てくるので、今後試してみようということで。。
最後に
簡単ですが、空間相関について隣接定義と各統計量についてまとめてみました。Vignettes以上にspdepを試した際は別途まとめられればと思います。
参考文献
- spdep(github)
- spdep(cran)
- 丸山 祐造, 空間的自己相関に関するモランの修正型I統計量
- Ogoke Uchenna Petronilla et al., Comparison Between Measures of Spatial Autocorrelation
- Gisliany Alves et al., Evaluating Social Distancing Measures and Their Association with the Covid-19 Pandemic in South America
- Cristina Gome et al., Characterizing the state and processes of change in a dynamic forest environment using hierarchical spatio-temporal segmentation