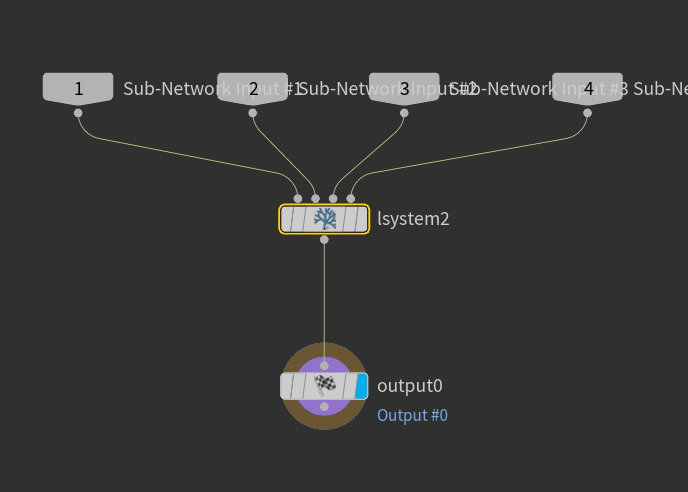
この記事はHoudini Advent Calendar 2020 15日目の記事です。
#はじめに
Procedural DesignのAkira Saitoです。
Houdiniを使用しロボットなどのメカデザインを自動で行う研究をしています。
Houdini Hive Japan 2020の「Procedural Hard Surface Design Vol.2」では、工程が進む毎に情報密度を上げていくようなメカデザインの自動生成ワークフローにおいて、ワークフロー初期の、形状の低周波領域(シルエット)を生成する仕組みの重要性と、その難しさに気付き、形状生成の起点にL-Systemを用いた考察とその成果を発表しました。
トーク後半の「L-System 2020」のおさらいと、紹介しきれなかたL-Systemの魅力をお伝えします。
#動作環境
Houdini 18.5.351
macOS Catalina バージョン10.15.7
MacBook Pro (15-inch, 2017)
プロセッサ 3.1 GHz クアッドコアIntel Core i7
メモリ 16 GB 2133 MHz LPDDR3
グラフィックス Radeon Pro 560 4 GB
#L-System 2020のおさらい
##L-Systemの基本(主要タートルコマンド)
L-Systemの各動作を表す１文字をシンボル(symbol)と言います。
主要なシンボルを以下にまとめました。
###進む
- F
- ValuesのStep Sizeで決められた長さの線を描画する。
- F(l) lで指定された長さの線を描画する。
- H
- ValuesのStep Sizeで指定された半分の長さの線を描画する。
- F(l) lで指定された半分の長さの線を描画する。
- f
- ValuesのStep Sizeで指定された長さ移動するが描画はしない。
- f(l) lで指定された長さ移動するが描画はしない。
- h
- ValuesのStep Sizeで指定された半分の長さ移動するが描画はしない。
- h(l) lで指定された半分の長さ移動するが描画はしない。
- G
- ValuesのStep Sizeで指定された長さ移動し頂点も生成しない。
- G(l) lで指定された長さ移動し頂点も生成しない。
- 補足
- F(l,w,s,d)と表記すれば、離lの他に、幅w、分割数d、断面数sも設定できます。
- "
- ValuesのStep Size Scaleで指定された値を長さに乗算します。
- "(s) sで指定された値を長さに乗算します。
###曲がる
- +
- ValuesのAngleで指定された角度で右に回転します。
- +(a) aで指定された角度で右に回転します。
- -
- ValuesのAngleで指定された角度で左に回転します。
- -(a) aで指定された角度で左に回転します。
- &
- ValuesのAngleで指定された角度でピッチアップします。
- &(a) aで指定された角度でピッチアップします。
- ^
- ValuesのAngleで指定された角度でピッチダウンします。
- ^(a) aで指定された角度でピッチダウンします。
- /
- ValuesのAngleで指定された角度で右にロールします。
- /(a) aで指定された角度で右にロールします。
- \
- ValuesのAngleで決指定された角度で左にロールします。
- \(a) aで指定された角度で左にロールします。
- ;
- ValuesのAngle Scaleで指定された値を角度に乗算します。
- ;(s) sで指定した値を角度に乗算します。
- |
- 180度回転します。
- *
- 180度ロールします。
###分岐
- [ ]
- [ ]ブラケット記号で囲むと、ラインを分岐させることができます。
###UP Vectorの可視化
L-Systemで立体的な構造を定義する場合、/や\によるロールをわかりやすく制御するために、up vectorの可視化をしましょう。
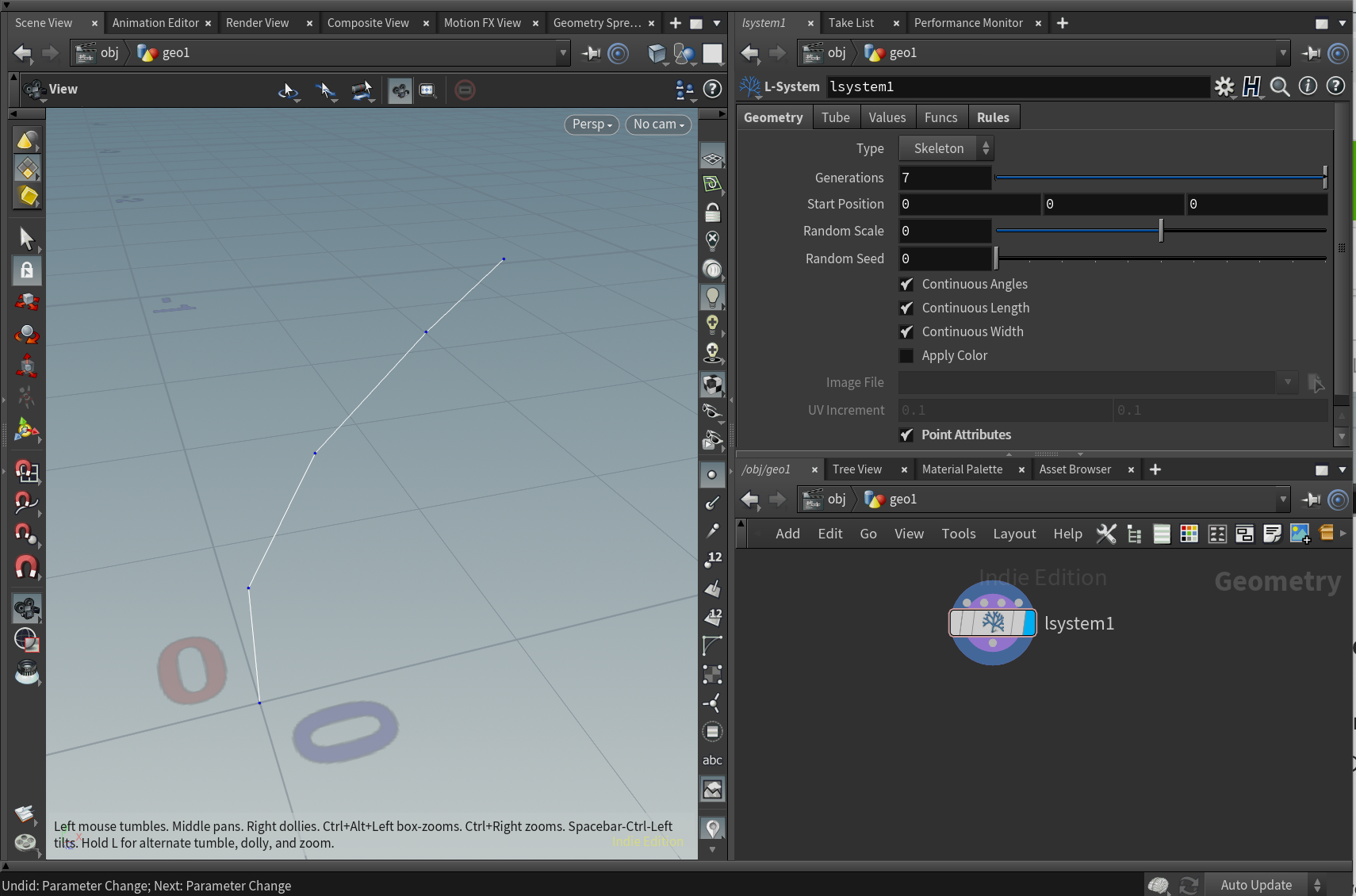
L-System SOPのGeometry項目内の、point Attributeを有効にし、UP Vectorを含む、様々な頂点アトリビュートを出力することができます。
出力された頂点アトリビュートのUP VectorをVisualize SOPで可視化します。これにより描画されたラインのロールを把握できるようになります。
##L-Systemの基本(再帰性)
###ルール
A = F[-F][F][+F]
のように、任意の1文字にL-Systemを定義しシンボルとして利用可能。
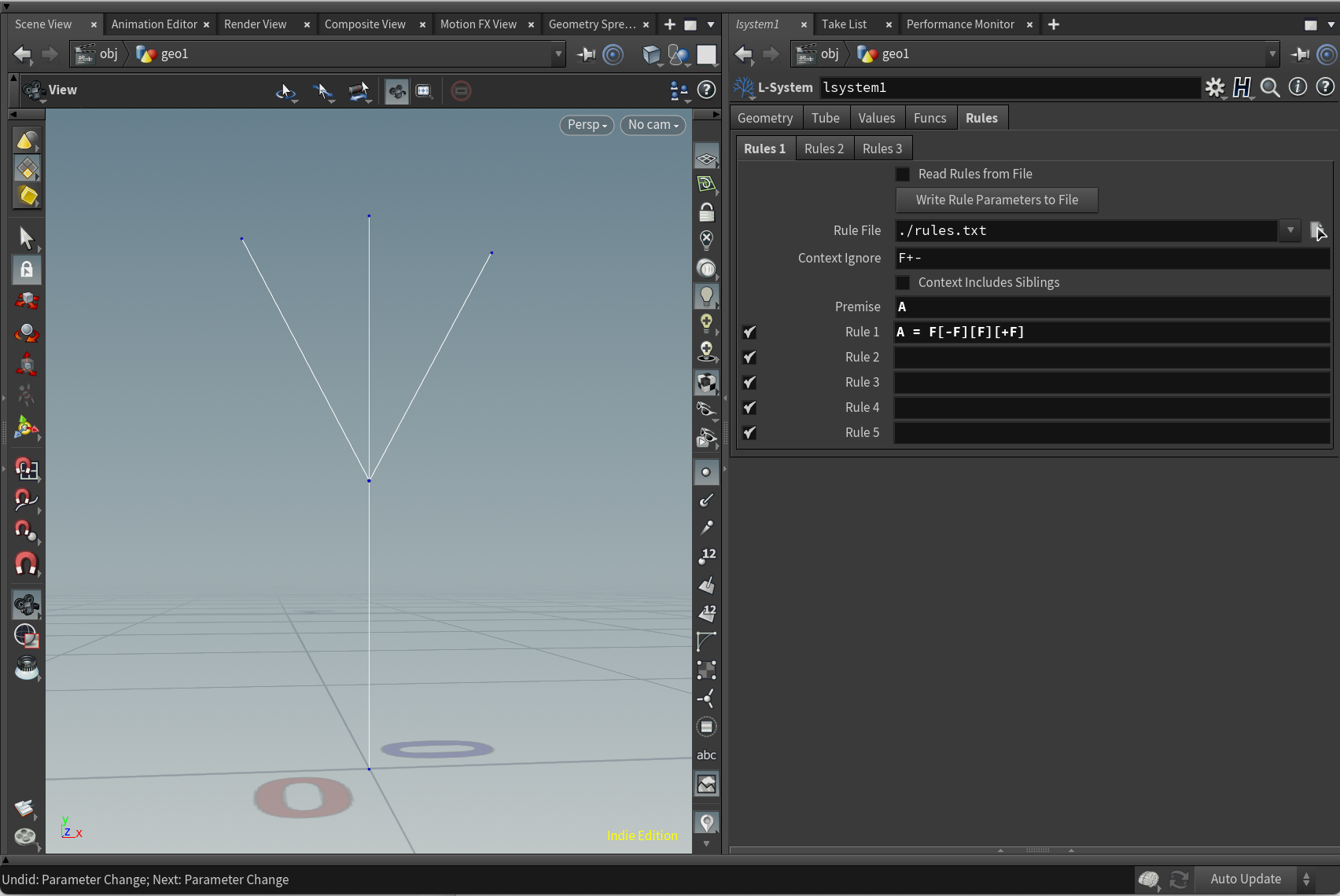
0 = FFFのように数字や、F=HHのように既存のシンボルも上書きして設定可能です。
###関数として
以下のように、シンボルの後に()を使えば、一般的なプログラム言語の関数のような使い方もできます。
A(a) = F[-(a)F][F][+(a)F]
A(30)のように使用すると、以下のように展開され実行されます。
F[-(30F][F][+(30)F]
###再帰性
A = FAのように、ルール内に自分自身を呼び出すような構造を再帰性と呼びます。
以下のようにAを呼び出す毎にルールが評価され、ルールそのものが成長していきます。
1段階目 A = FA
2段階目 A = FFA
3段階目 A = FFFA
4段階目 A = FFFFA
L-SystemではGeometry項目内のGenerationsの回数ルールが評価されます。
Generationsが4の場合A = FAはラインを4回描画します。
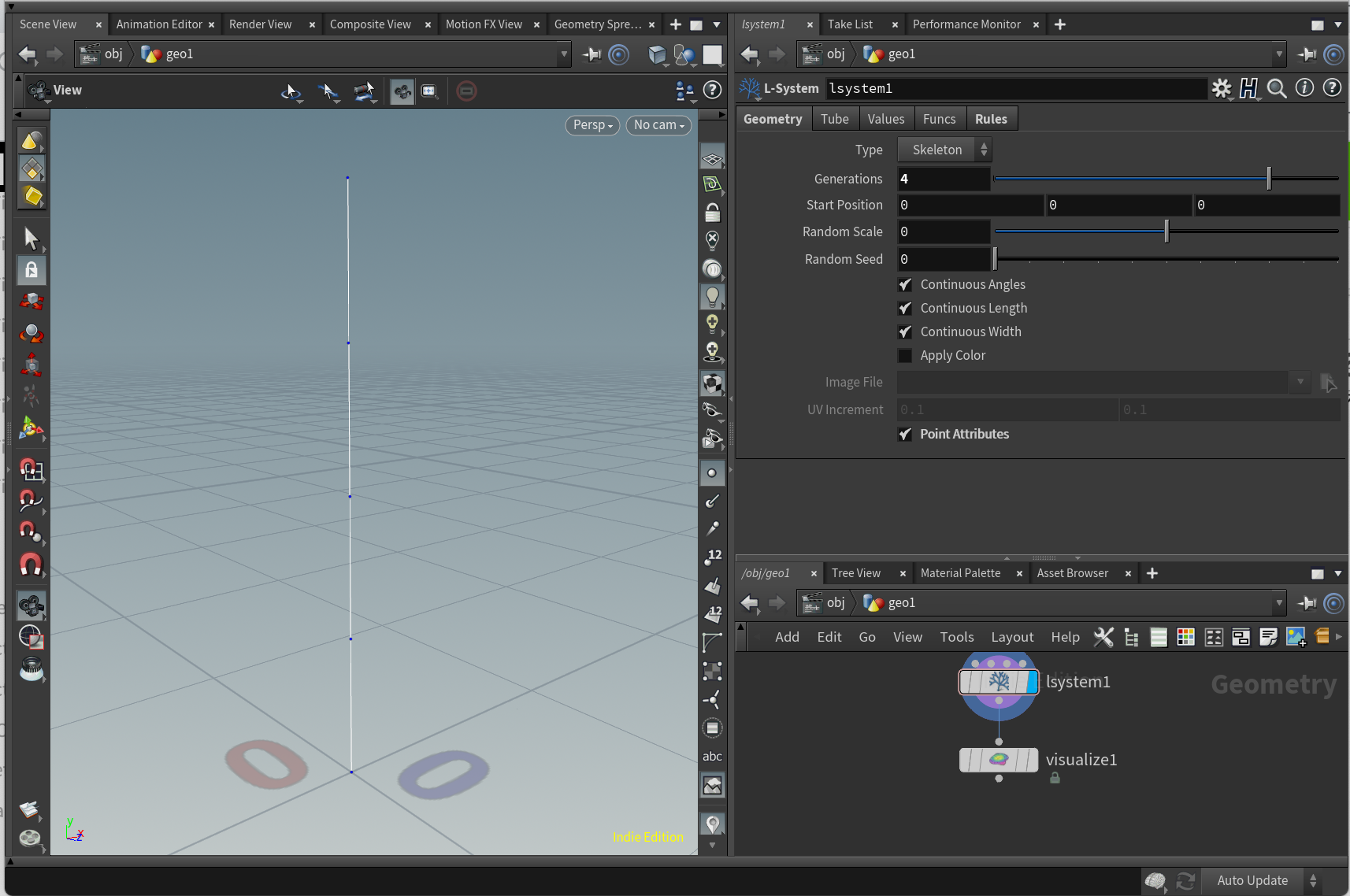
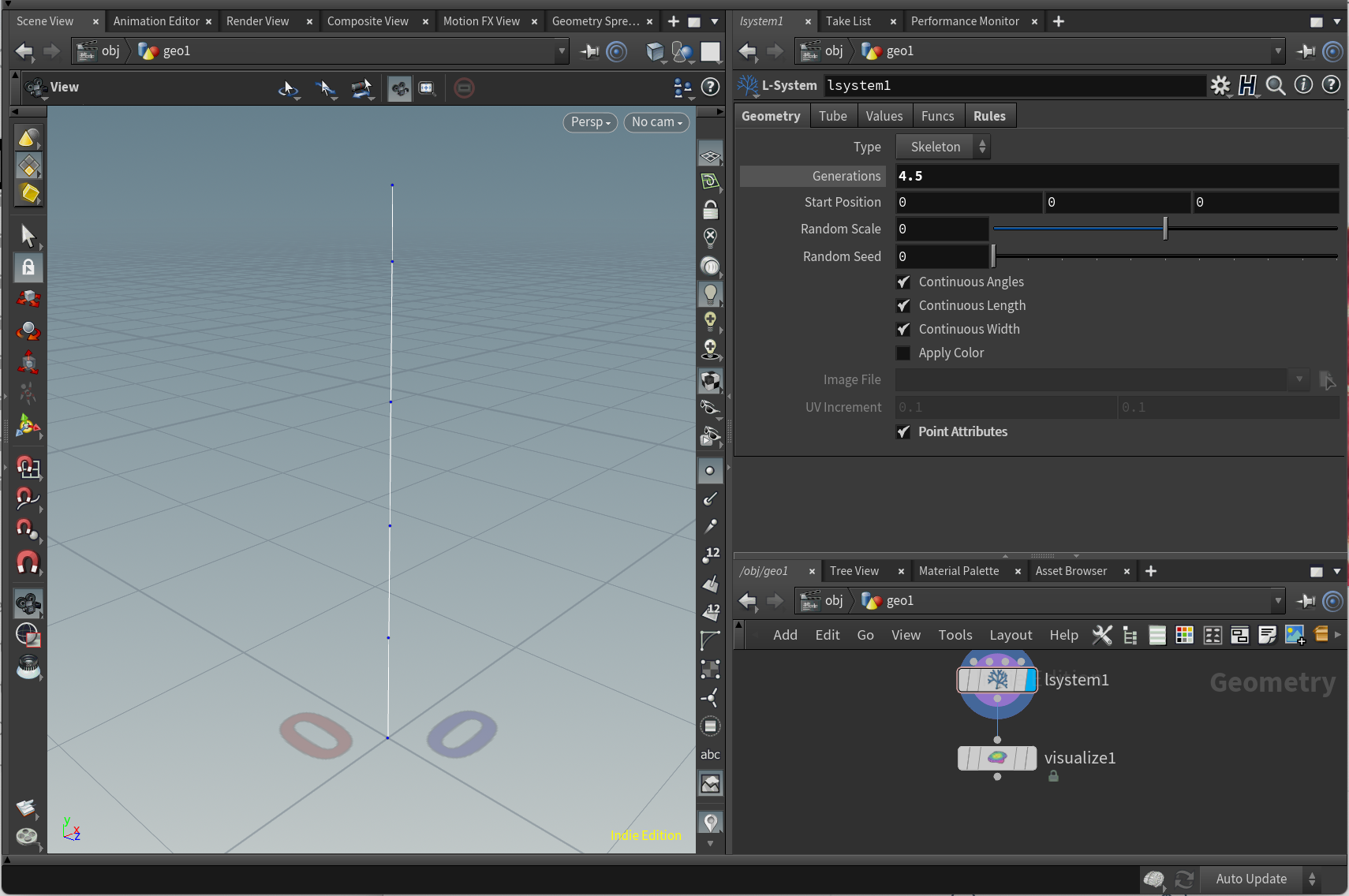
Generationsには少数を設定できます。その場合、小数点以下の値は、生成される最後のルールの長さや角度に乗算されます。
Generationsが4.5の場合A = FAはラインを4回に続き0.5倍の長さのラインが描画されます。
##L-Systemの応用
###左右対象
S = |*"(-1)
|で180度回転させ、*で180度ロール、"(-1)で長さを-1乗算することにより、それ以降のL-Systemを左右反転することが可能です。
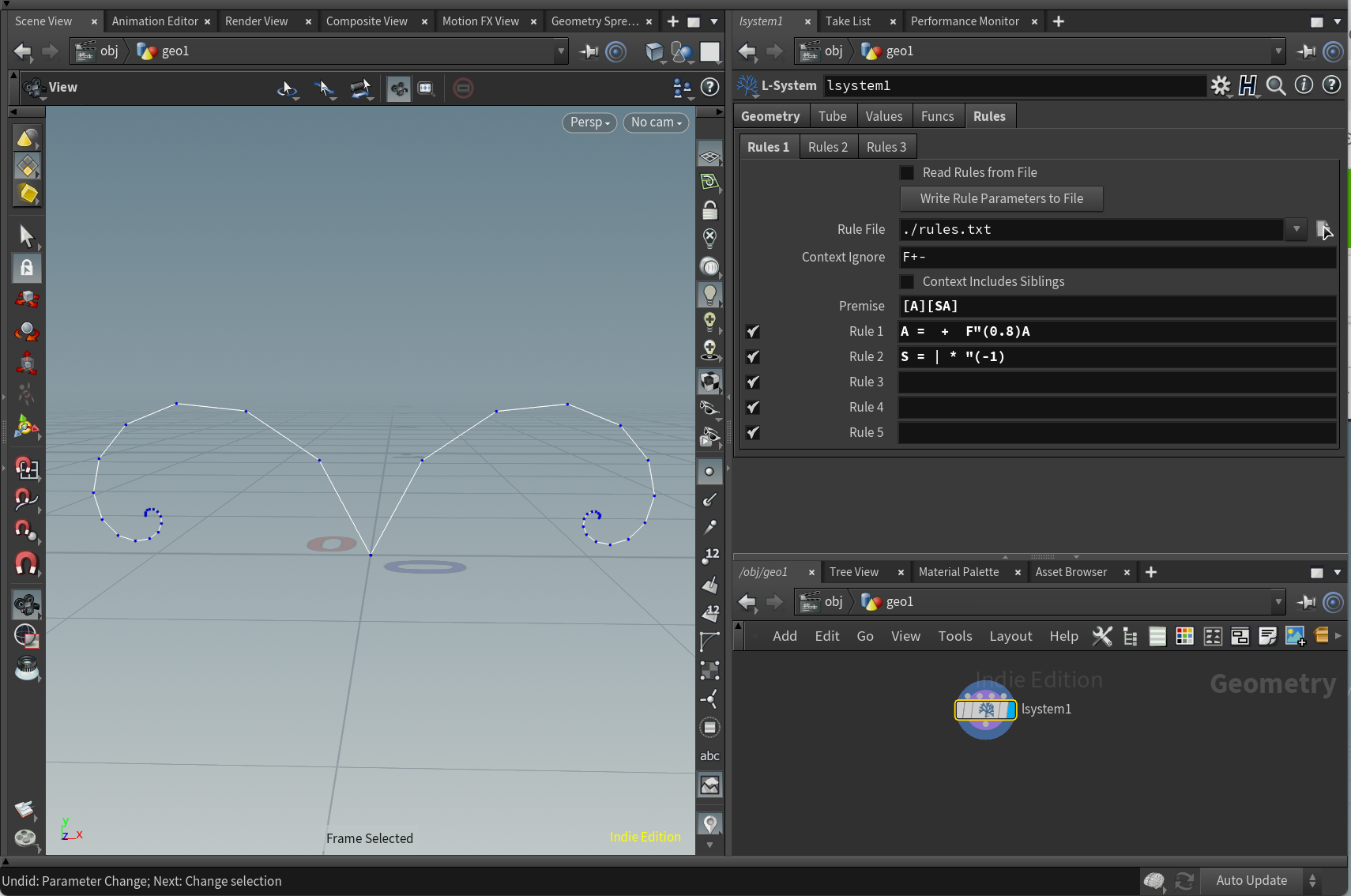
UP Vectorが反転するので注意!!!
回避することが出来たら教えてください…
###グループ化
- g(n)
- Funcs項目内のGroup Prefixで指定した文字列の後にnで指定した数字が入った名称のグループを生成します
##L-System SOPのUIカスタマイズ
複雑なL-Systemを構築する場合、標準のL-System SOPのUI(Parameters)では、編集しづらい場合もあるので、HDAによるUIのカスタマイズをお勧めします。
-
Generationsをいつでも編集可能にする。
-
Geometry Values Funcsの三項目はRuleと同時に編集可能にする。
-
Ruleは利用可能な25個全て表示。
-
初期形状は人体(これはお好みで)。
-
左右反転のルールSをデフォルトで定義。
-
標準のL-Systemを内包し、UIのみカスタマイズしたHDAとして実装。
##作例紹介
これまで紹介したL-Systemの昨日で、ロボットやクリーチャーなど、四肢など分岐を持った構造の定義ができるようになります。数点、その作例を紹介します。
###人型
Angle = 10
Premise = [A [B] [SB] [D]] [C] [SC]
A = g(1) HHHH
B = g(2) +(90) H +(60) "(1.6) & F ^^ F
C = g(3) +(90) H +(80) "(1.8) ^ F && F ^^ H
D = g(0) H
S = | * "(-1)
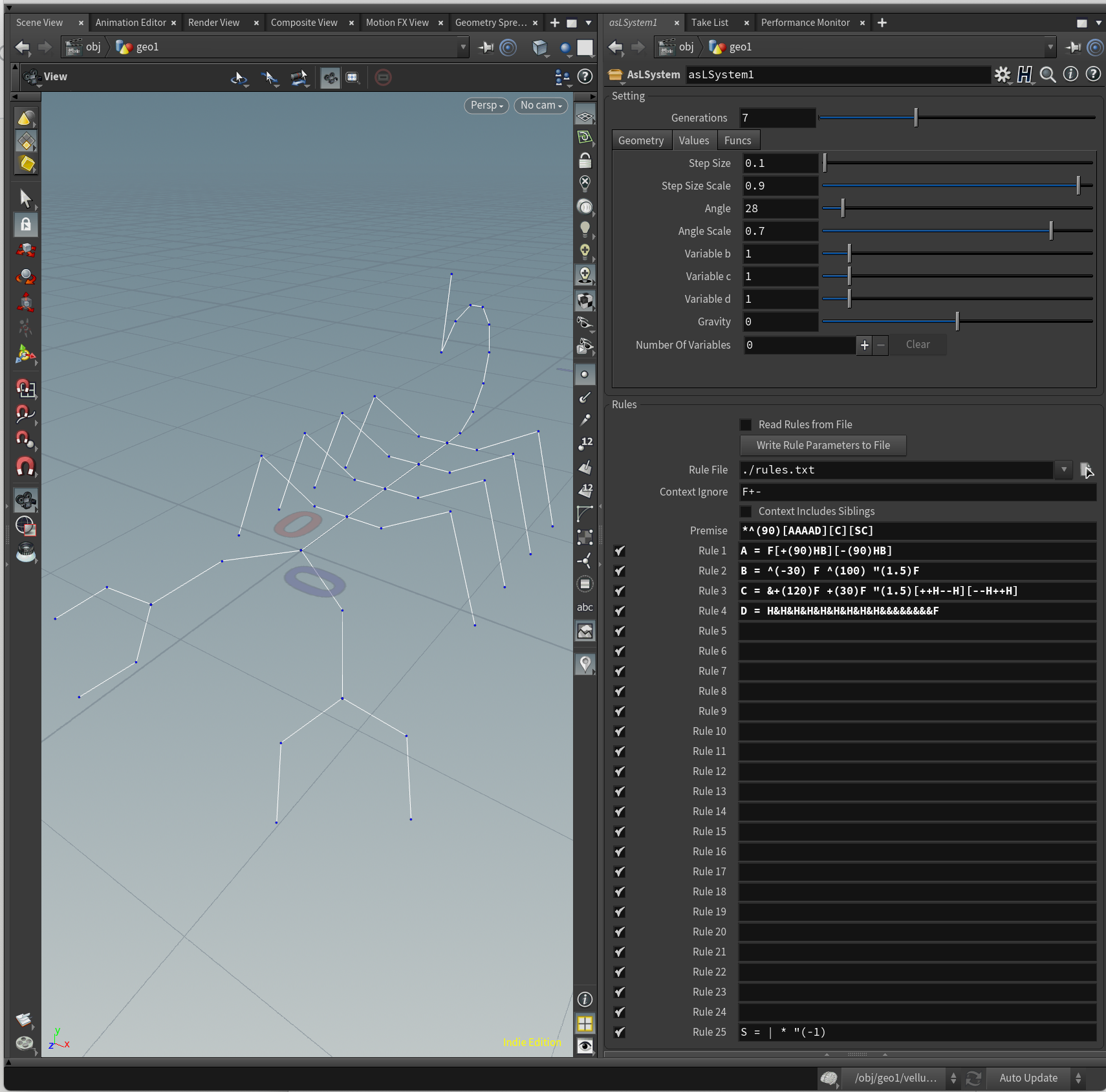
###サソリ
Angle = 28
Premise = *^(90)[AAAAD][C][SC]
A = F[+(90)HB][-(90)HB]
B = ^(-30) F ^(100) "(1.5)F
C = &+(120)F +(30)F "(1.5)[++H--H][--H++H]
D = H&H&H&H&H&H&H&H&H&&&&&&&&F
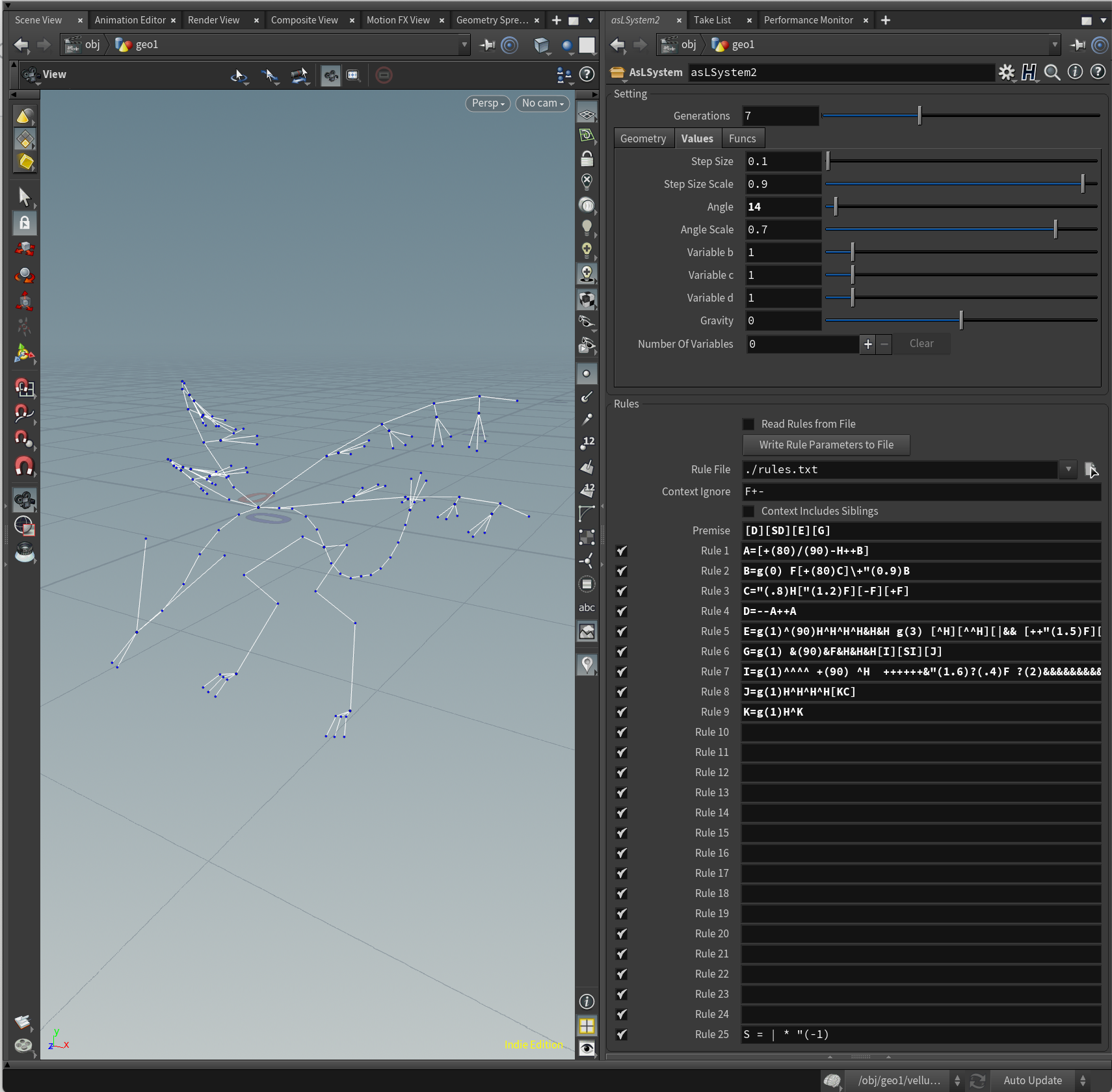
###ドラゴン
Generations = 7
Angle = 14
Premise = [D][SD][E][G]
A = [+(80)/(90)-H++B]
B = g(0) F[+(80)C]\+"(0.9)B
C = "(.8)H["(1.2)F][-F][+F]
D = --A++A
E = g(1) ^(90)H^H^H^H&H&H g(3) [^H][^^H][|&& [++"(1.5)F][--"(1.5)F]]
G = g(1) &(90)&F&H&H&H[I][SI][J]
I = g(1) ^^^^ +(90) ^H ++++++&"(1.6)?(.4)F ?(2)&&&&&&&&&F ^^^^^^F "(.5)^^^^^[H&&&H][-H&&&H][+H&&&H]
J =g (1) H^H^H^H[KC]
K = g(1) H^K
#++
ここまで紹介した機能で、ロボットやクリーチャー等の基本的な骨格の定義は可能ですが、ここからは「L-System2020」で紹介しきれなかったいくつかの仕様を紹介します。
##Probability(可能性)
A = +F A :0.8
このように、ルール設定最後の:(コロン)と数値により、そのルールが有効になる確率を設定することが出来ます。
このルールは80%の確率で有効になり、残りの20%の確率では何も行いません。
Premise = A
A = +F A :0.5
A = -F A :0.5
上記のようなL-Systemでは、Aというルールは+F Aと-F Aがそれぞれ50%の確率、すなわち、そのどちらかが有効になります。
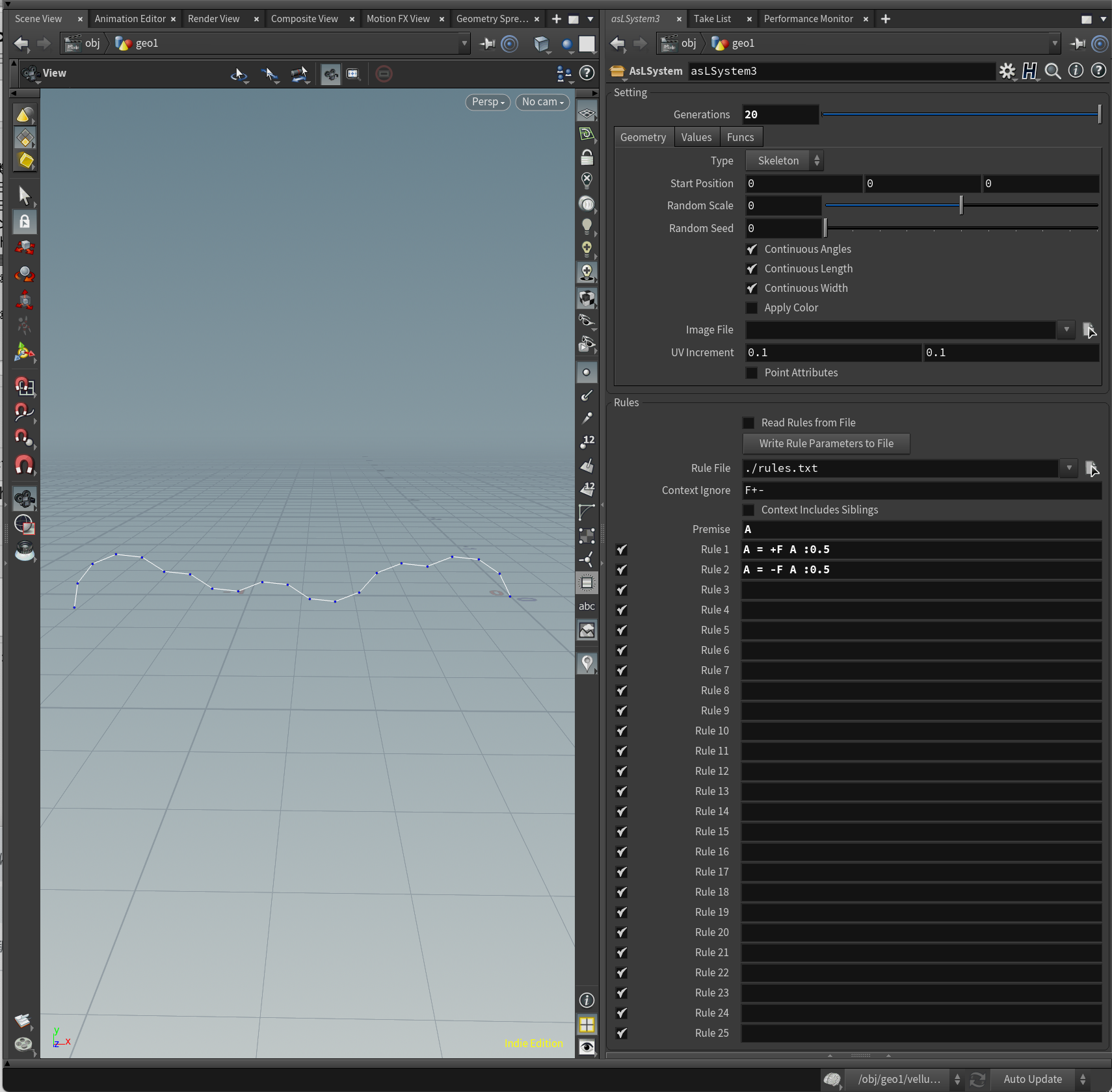
このように、左右ランダムに曲がるラインを描画することが可能です。
Premise = A
A = +F A :0.8
A = -F A :0.2
確率に偏りを与えることで、面白い表情のラインの描画が可能です。
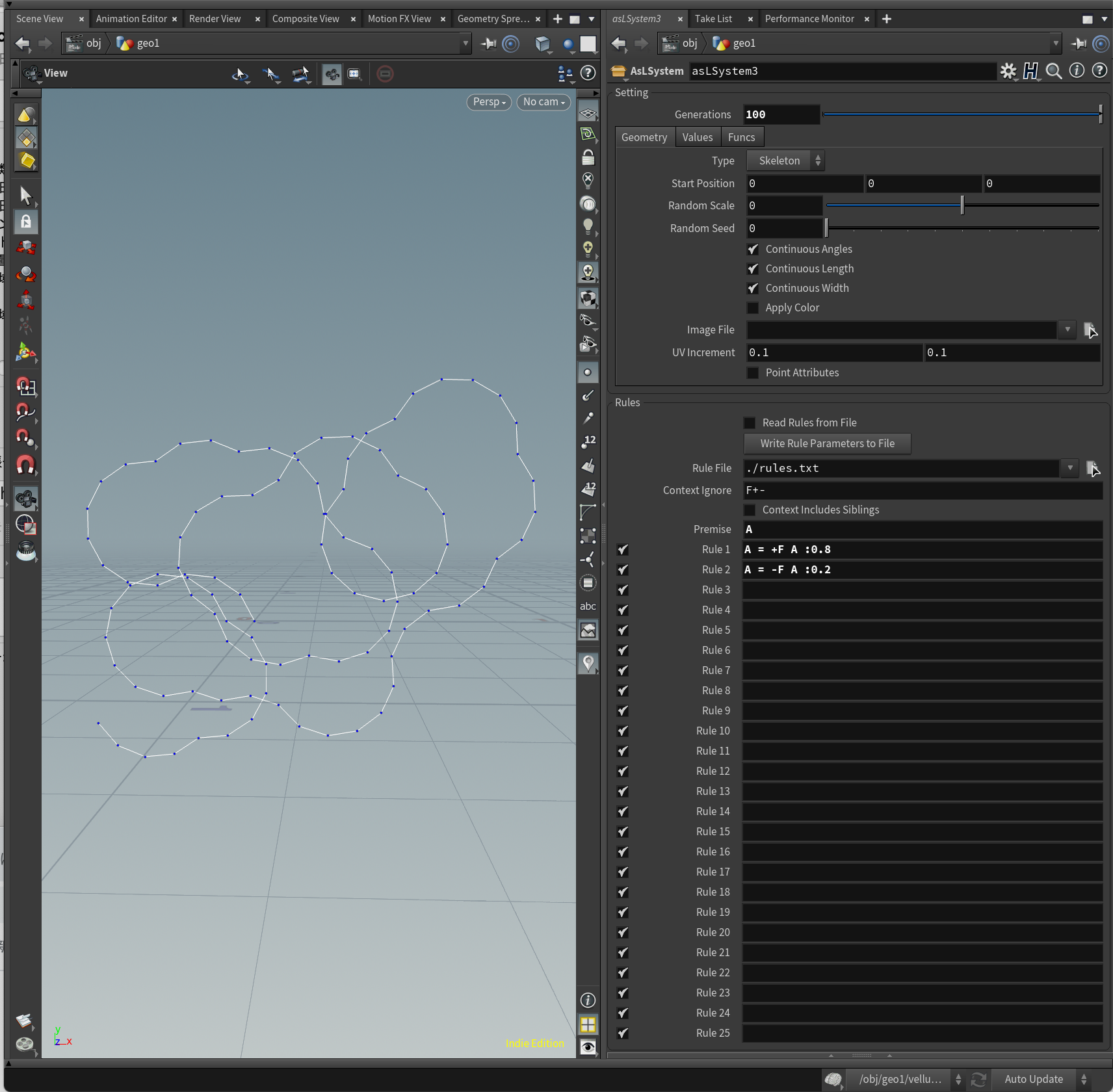
確率の振る舞いは、Geometry項目内のRandom Seedに依存しています。
##ローカル変数と条件分岐
###ローカル変数
Values項目内の、Variable b c d に値を設定しそれぞれをL-Systemのルール内で変数として使用することが可能です。
Generationsをch("generations")で変数に代入し、L-Systemのルール内から参照することは非常に有効なテクニックです。
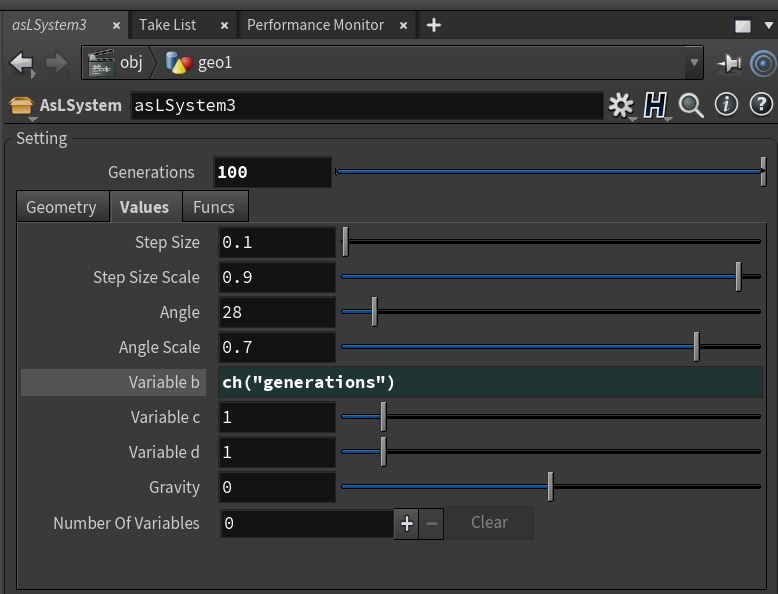
他によく使う変数としては現在位置がわかるx,y,z現在の角度が代入されるa。現在の繰り返し回数のtなどがあります。
###条件分岐
シンボルの後ろの:(コロン)の後に書かれる条件がTrue(真)の時、そのルールは有効になります。
Variable b = ch("generations")
Premise = A
A :b!=t = FA
A :b=t = F[-F][F][+F]
変数bにはGenerationsが設定され、変数tには自動で現在の繰り返しか数が代入されています。結果、b=tになるまではF = FA、b=tすなわち繰り返しの最後にA = F[-F][F][+F]となります。
このように、末端に特別な形状を生成することが可能になります。
Premise = A
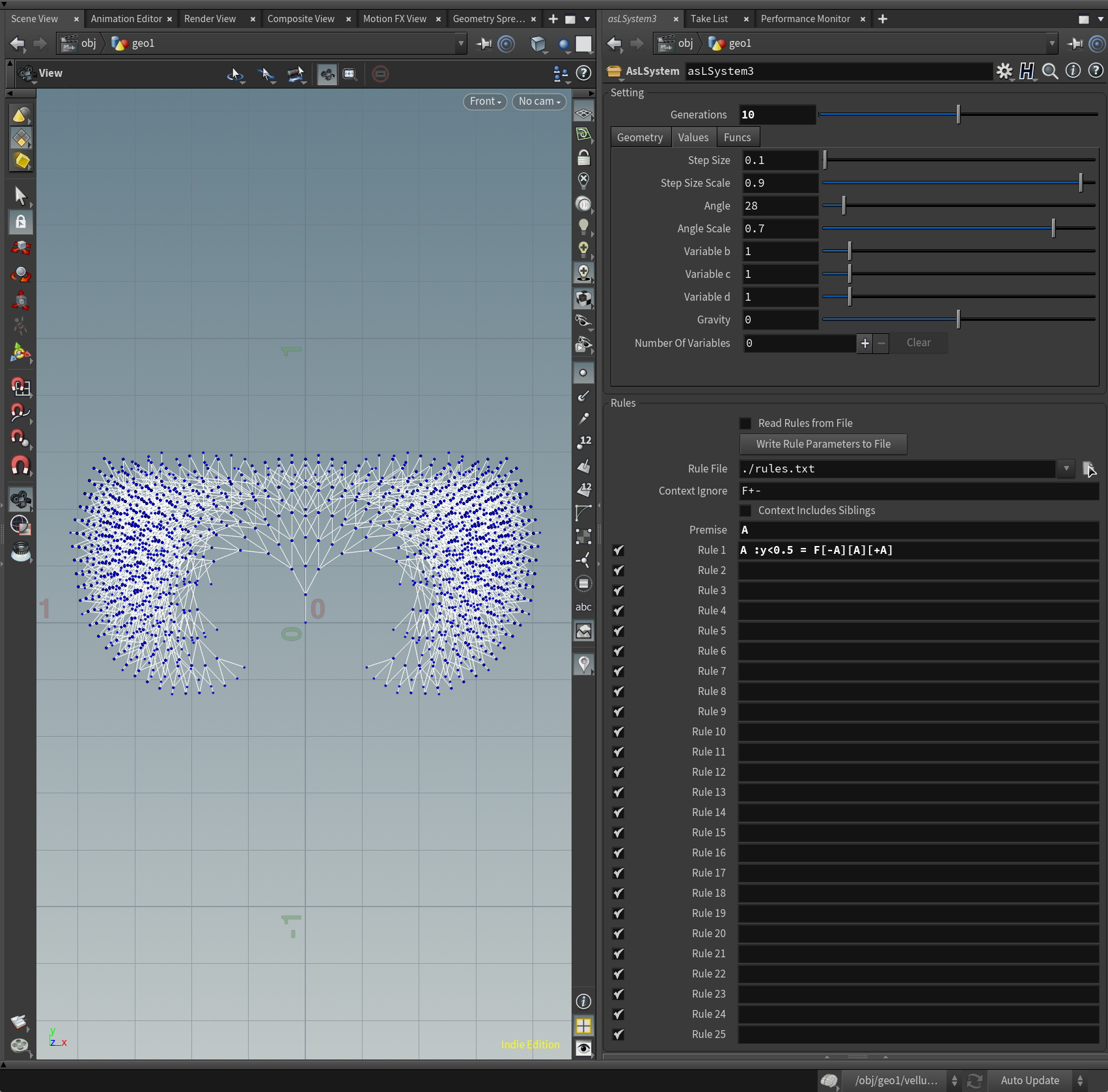
A :y<0.5 = F[-A][A][+A]
現在位置のy座標が0.5未満の場合、A = F[-A][A][+A]というルールが有効になり、y座標が0.5以上の場合は何も行いません。y座標0.5以上の生成を止めることが可能です。
Premise = A
A :t%2=1 = F[-F][A][+F]
A :t%2!=1 = FA
このようなルールでは、t%2=1という条件、現在の繰り返し回数tを2で割った余りが１のとき、すなわち奇数回ではA=F[-F][A][+F]となり、偶数回ではA=FAとなります。
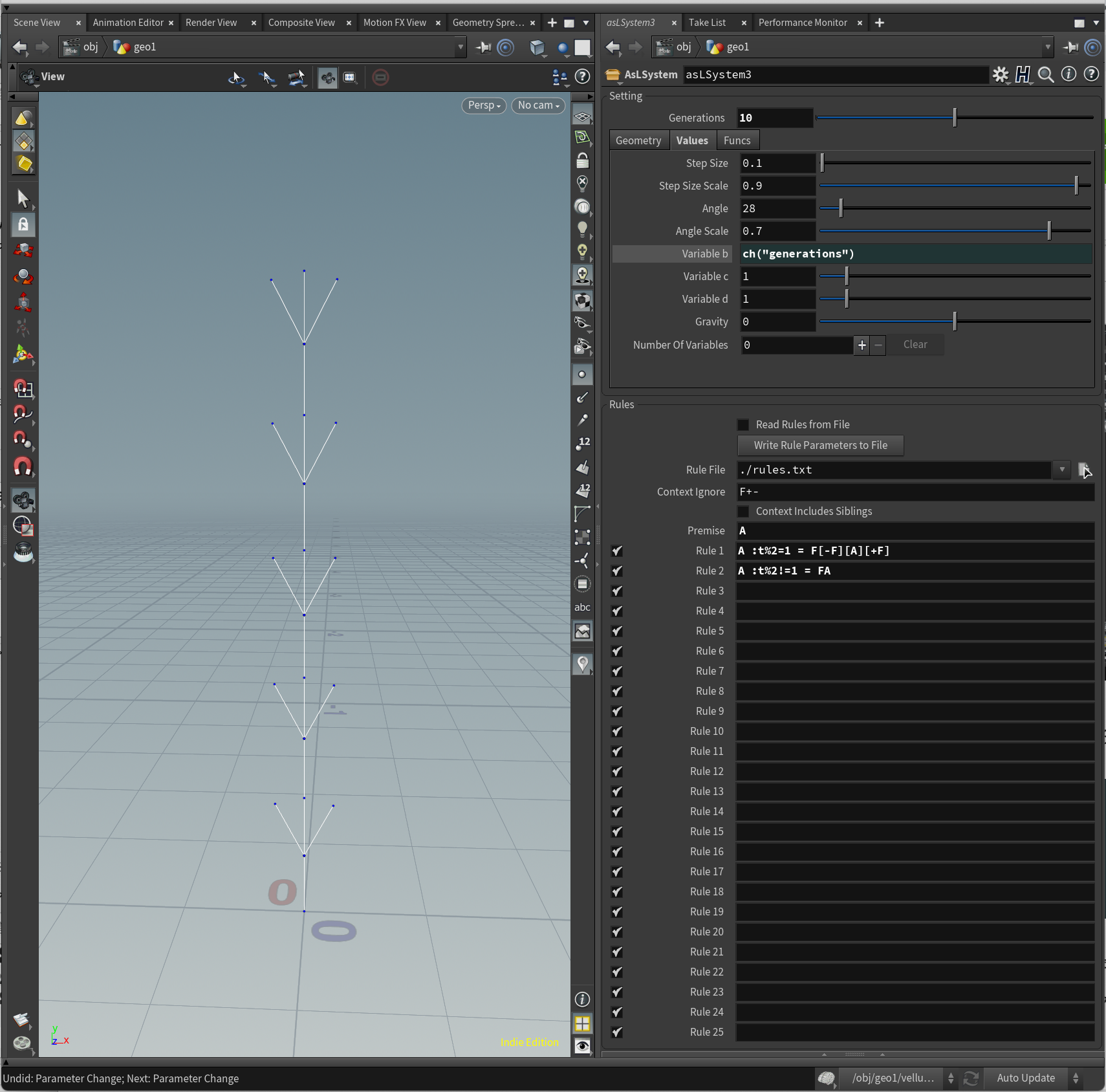
条件によりルールを変化させることで、より複雑な構造を生成することが可能になります。
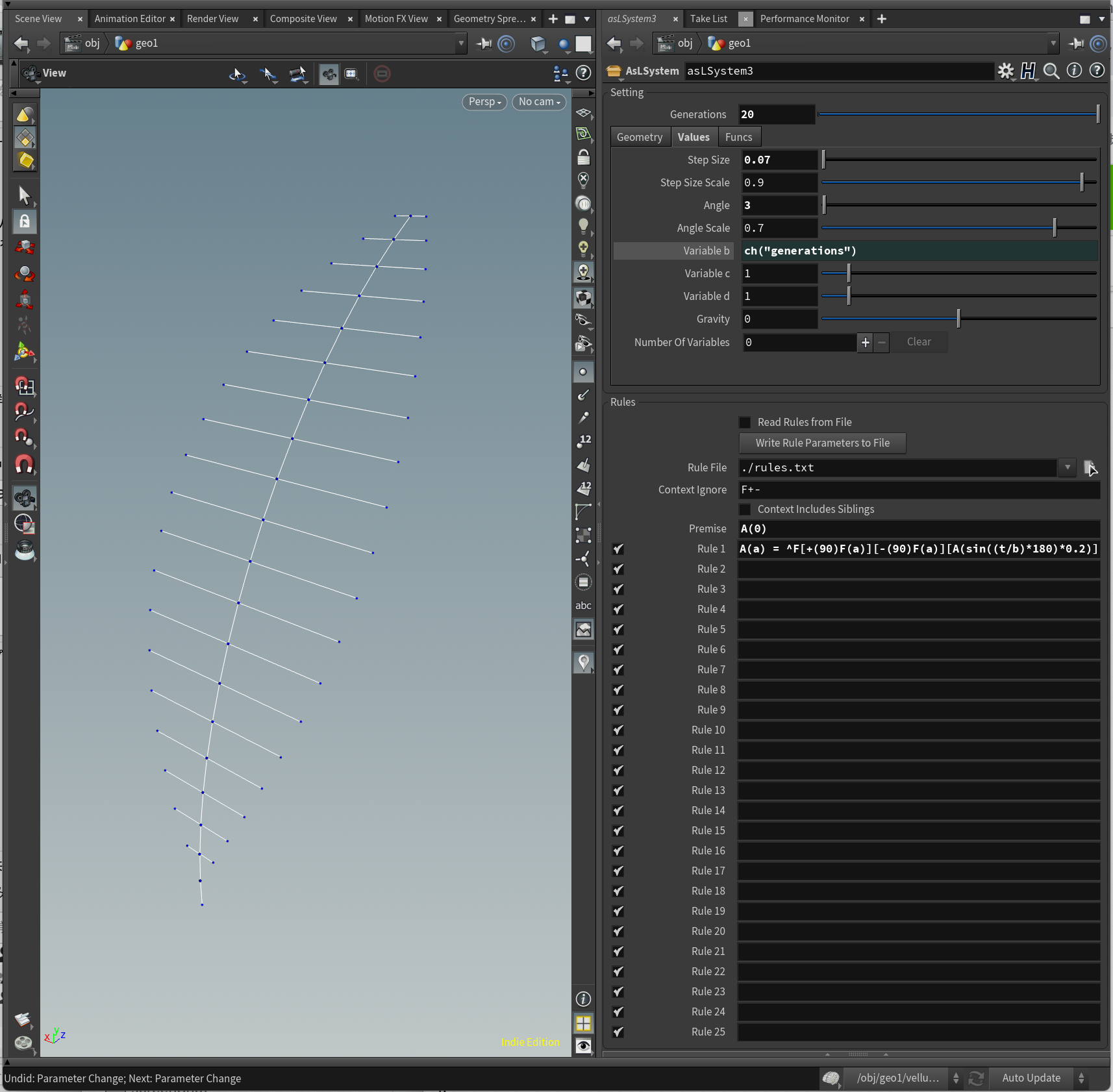
###ローカル関数
三角関数sin(angle) cos(angle)や、min(a,b) max(a,b)など、ローカル関数が数種類用意されており、それらをL-Systemのルール内で使用できます。
Variable b = ch("generations")
Premise = A(0)
A(a) = ^F[+(90)F(a)][-(90)F(a)][A(sin((t/b)*180)*0.2)]
三角関数のsinで葉のような形状の幅を設定しています。
##context(文脈)
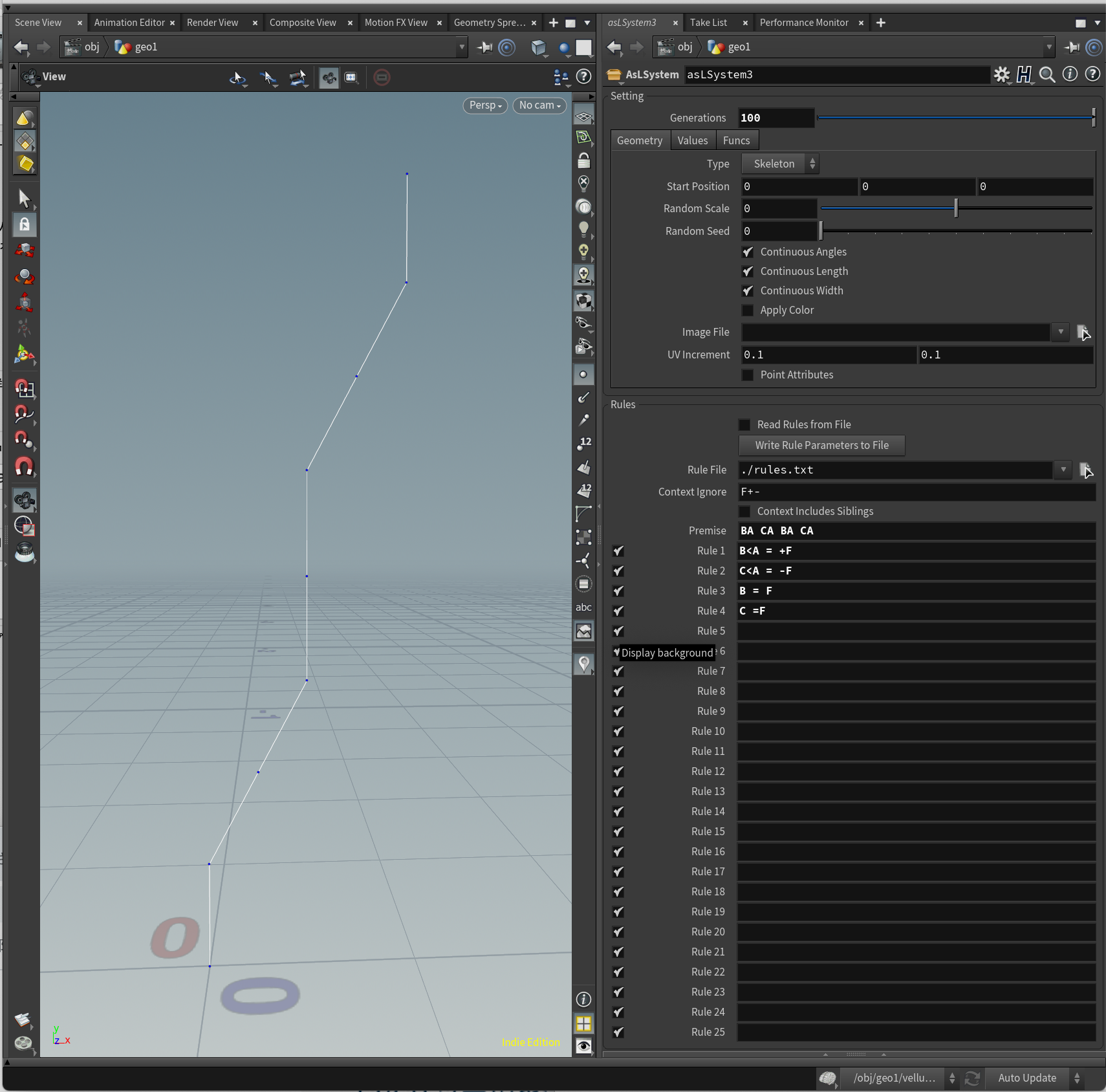
Premise = BA CA BA CA
B<A = +F
C<A = -F
B = F
C = F
このようなL-Systemの場合、
B<A = +Fは、Aというシンボルを+Fというルールで定義しているのですが、シンボルのAの前にある<によりcontext(文脈)という条件が設定されます。
この条件は<の前にあるBとAが連続したときに有効になるルールです。
BAと続いた時は+FとなりCAと続いた時は-Fとなります。
Premise = AB AC AB AC
A>B = +F
A>C = -F
B = F
C = F
先ほどとは異なり、A>B = +FはAの後の>Bにより、ABと続いた時に有効になるルールを定義することが可能です。
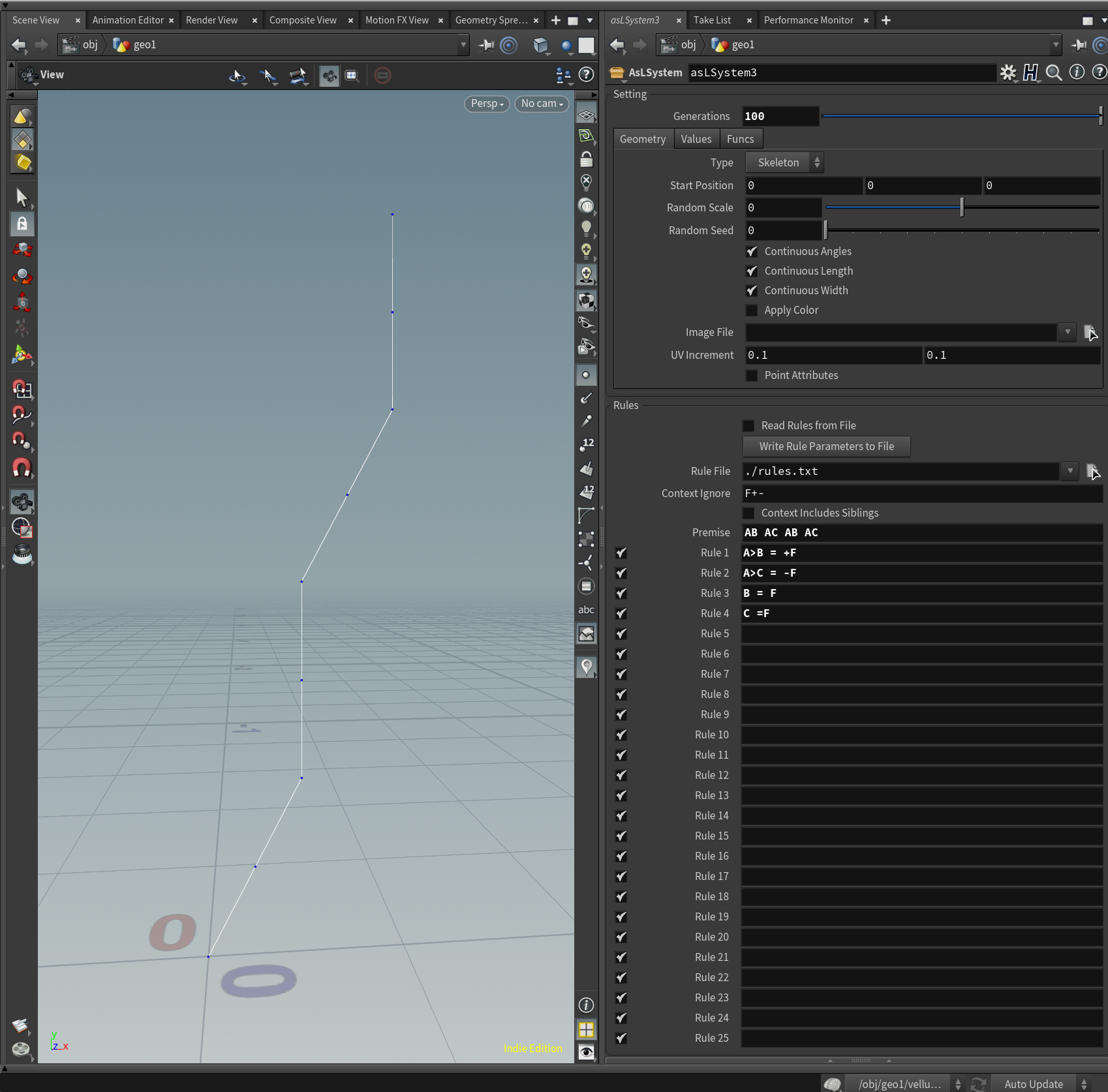
このようにABと続いた時は+FとなりACと続いた時は-Fになります。
B>A>B = +F
B>A>C = =F
C>A>B = ^F
C>A>C = &F
定義したいシンボルの前後の繋がりでルールを変化させることも可能です。
Context Ignoreで指定されたシンボルはContextの条件から除外されます。
デフォルトのF+-の状態ではこの３文字がContextの条件から除外され、
Premise = B-A C+A
B<A = +F
C<A = -F
B = F
C = F
上記のようなPremiseでもContext上では-と+は無視され、B-AはB＜A、C+AはC＜Aと同一のContextとして処理されます。
##L-System2020++作例
####人型(手を追加)
Premise = [A [B] [SB] [D]] [C] [SC]
A = g(1) HHHH
B = g(2) +(90) H +(60) "(1.2) & F ^^ F "(0.4)\(180)O
C = g(3) +(90) H +(80) "(1.6) ^ F && "(1.4)F ^^ "(.8)H
D = g(0) "(0.3)HH "(3)H
//hand
O = g(4)[P][-(10)"(.9)P][-(20)"(.7)P][+(10)"(.95)P][/(20)+(30)"(.8)Q]
P = F &(10)"(.3)F &(10)"(.8)F &(10)"(.6)F
Q = F &(10)"(.3)F &(10)"(.6)F
S = |*"(-1)
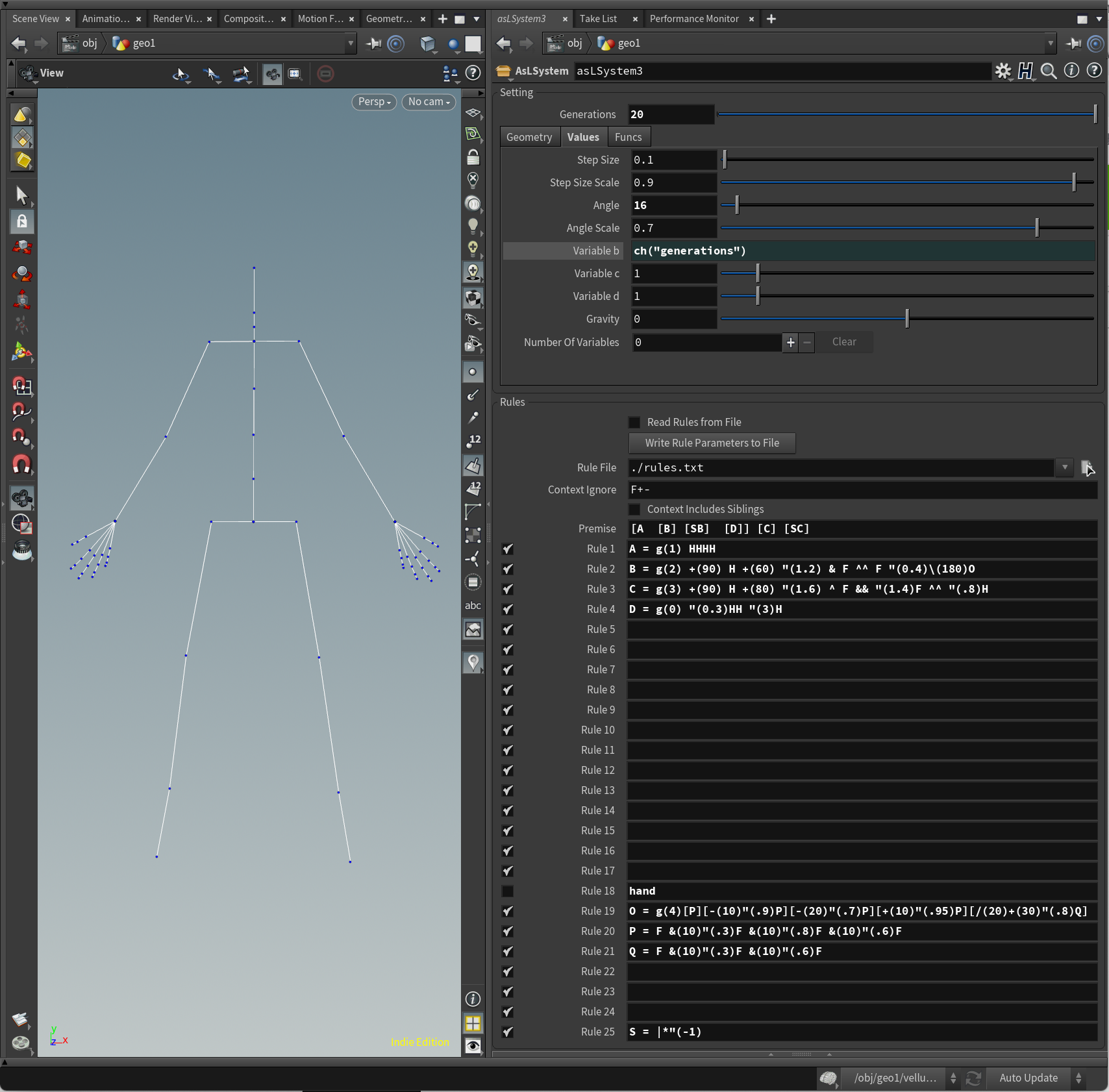
ルールのチェックボックスをOFFにしてコメント行として使うと可読性が少しだけ上がる(気がします)
条件分岐などを使用した作例を近日中に書きます…
#まとめ
何らかの形状を自動生成する際、起点のSOPノードを何にするのかは、その後のワークフローへの影響は大きく非常に重要です。アートディレクタブルな形状生成実現のために、コンピューターグラフィックの古典的な技術、L-Systemを用いてみてはいかがでしょうか？この記事が、そのお役に立てれば何よりです。
#L-Systemの学習に役立つ情報
####公式ドキュメント
https://www.sidefx.com/ja/docs/houdini17.5/nodes/sop/lsystem.html
####北川さんのHoudini Advent Calendar2016より
http://nomoreretake.net/2016/12/15/houdini_l-system_intro/
####サルにもわかる Houdini
http://ikatnek.blogspot.com/2017/03/l-system.html
####公式チュートリアル動画 Magic Market | L-Systems
https://www.youtube.com/watch?v=0vE8GiXhOWM