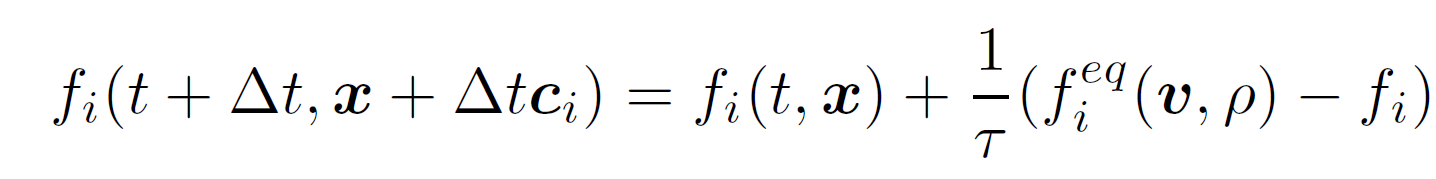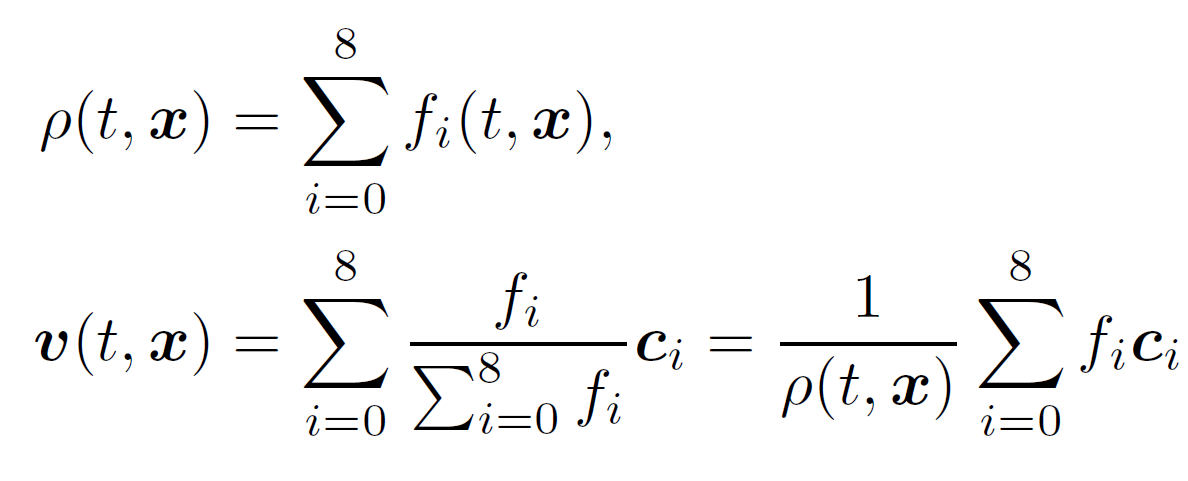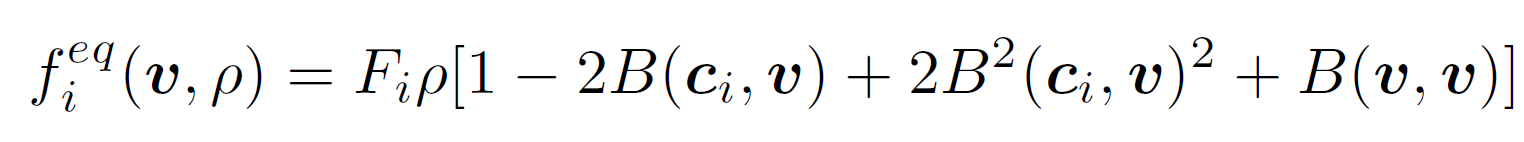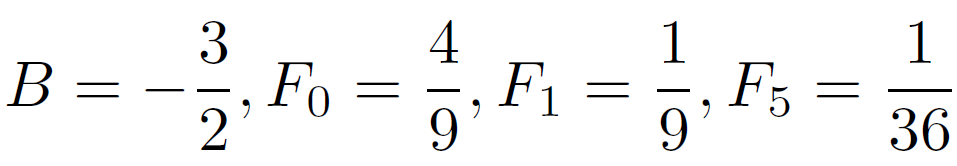格子ボルツマン法による流体の数値計算
格子ボルツマン法とは
水や空気などの流体の運動を数値的にシミュレーションするための方法の一つです。
流体の運動をシミュレーションする際に、よく使われるのが、流体の基礎方程式であるナヴィエ・ストークス方程式を数値計算するというものです。
それに対して、格子ボルツマン法では、もうちょっと「雑な」アプローチをとります。
まず空間を格子に分割して、水や空気の粒子は全て格子点の上を動きまわるものとします。
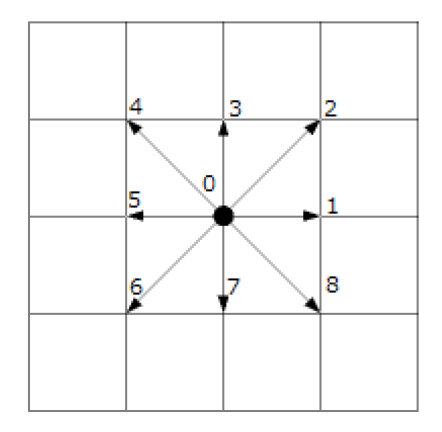
これは2次元の場合の図になりますが、このとき粒子はその場に留まり続けるか、隣の格子に移動するかの9通りの運動しかできません。
雑ですね。
このような格子モデルをD2Q9モデル(2次元かつ9通りの運動が可能)といいます。3次元の流体の運動に対しては、また別の格子モデルがあります。
さて、格子点上にある粒子は、次の瞬間には(留まるものを除いて)隣の格子点に流れていってしまいます。しかし、同時に隣の格子点からも粒子が流れ込んできます。これを粒子の併進と呼んでやります。
こうして流れ込んできた粒子たちは「衝突」して、あるものは衝突によって運動のパターンを変えたり、あるものは変えなかったりします。
この「併進」と「衝突」を繰り返すことで、流体の運動が実現するというのが格子ボルツマン法の基本的な発想です。
格子BGK方程式
上記のような粒子の併進や衝突を以下のような格子BGK方程式で表現します。
ここで $t$ は時間、 $i = 0 \dots 9$ でD2Q9の図に対応した粒子の運動方向、$f_i$ は $i$ 方向の粒子の数密度、$f_i^{eq}$ は $i$ 方向の局所並行分布関数をあらわすものとします。
$v$ は流体の流速、$\rho$ は流体の密度ですが、粒子の数密度を使って強引に
と表せるものと考えます。
格子BGK方程式では、衝突過程を局所平衡分布関数 $f_i^{eq}$ に緩和する過程であるとみなしています。
その局所平衡分布関数とは、簡単に言うと粒子の平均速度が $v$ で与えられるような「正規分布」なのですが、計算の都合上多項式で近似して
としています。ここで
ですが、 $F_1 = F_2 = F_3 = F_4, F_5 = F_6 = F_7 = F_8$ です。これはD2Q9モデルの場合の値です。また、この値は格子BGK方程式がナヴィエ・ストークス方程式を復元できるように計算された値でもあります。
境界条件の処理
他の数値計算方法と同じく、格子ボルツマン法でも境界において特別な処理が必要となります。
例えば、境界が壁であるケースです。壁の外には粒子は出ていかないし、また壁の外から粒子がやってくることもありません。
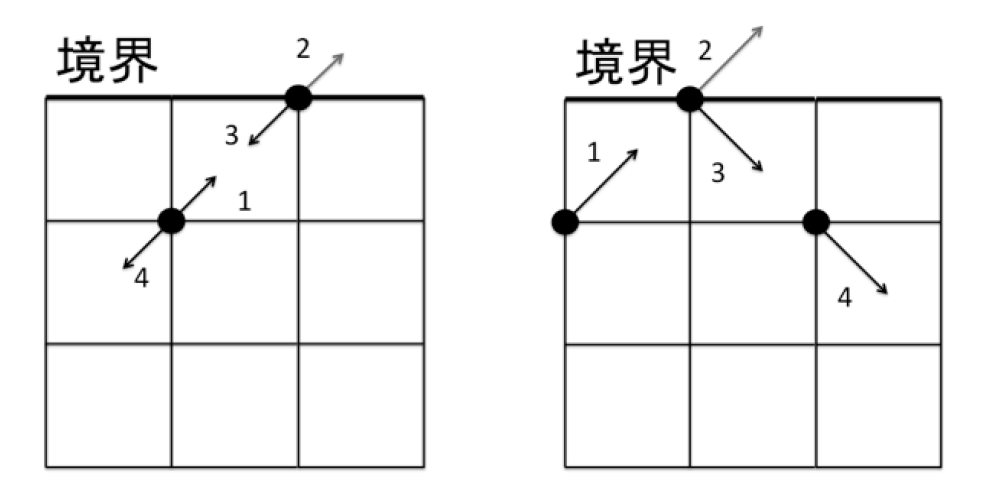
どちらの図も粒子は「1→2→3→4」の順で運動しています。「2→3」の部分が境界条件の適用による粒子の運動です。
左の図は、単純に壁にぶつかって跳ね返るという「Bounce-back」の境界条件を表しています。物理的には壁の上で流体の速度が0であるという条件でもあります。
一方、右の図はそれとは逆に壁にぶつかった粒子が「滑る」境界条件をあらわしています。
まとめ
以上のように
- 格子BGK方程式に基づく粒子の衝突
- 粒子の併進、あるいは境界条件の処理
を繰り返していくことで流体の運動を計算することができます。
もちろん「流体の運動を計算することができる」というためには、格子BGK方程式から「何らかの操作」をほどこすことで流体の基礎方程式であるナヴィエ・ストークス方程式を復元できることが必要です。
今回はそこまではやりません。
また併進過程において近接格子とは粒子(データ)のやりとりが発生するのを除くと、基本的にはそれぞれの格子点上で計算を進めることができます。numpyが縦横無尽に活躍しそうですね。GPUを用いた計算も簡単にできそうです。
くたばれFORTRAN!!
さてお待ちかね、Pythonのコードです↓↓↓↓
Pythonコード
なんとここでタイムアップ!
書ききれませんでした〜
気が向いたら追記します :dogeza:
おわりに
Pythonを使って格子ボルツマン法による流体シミュレーションをやってみましたることができませんでした。
いかがでしたか?
おわびに
すいませんでした。
アルゴリズムとしてはそこまで難しくはないため、何となく動くコードを書くことも難しくないと思います。
実用的なコードを書こうと思った場合は、ハードルが多少上がります。
格子のモデルや格子BGK方程式の詳細、境界条件の処理方法は各種の論文をざっと読んでトレンドを押さえておくというのが基本で、本はあまり買わない方が良いです。
論文を読むとはいっても、基本的なアルゴリズムはここで書いたものとそうかわらないため、書かれている内容を追いかけることはそれほど難しくありません。
例えば境界条件の処理一つを取ってみても、今回紹介した方法は小学生でもわかるくらいシンプルですが、その分シビアな計算をしようとするとそこから簡単に発散します。実用的なコードを書く場合は、古い論文ですが、最低限この方法で境界条件を処理するのがよいかと思います。
なおマイクロアドでも格子ボルツマン法は特に使っていません。
ではまた〜