ごあいさつ
おはようございます、ポート株式会社の鈴木です。これから、社内で開催されている技術共有会の成果をQiitaで公開していきます。
はじめに
球面である地球上でその表面の特定の1点を表現するために、古来から緯度と経度という概念が使われてきた。これは情報化が進んだ現代社会においてもそのまま使用されている。当記事では2点の緯度と経度が与えられた時、その2点間の距離を求める方法を説明する。
なお、説明のために高校数学3・C程度の知識を用いる。
動機
RubyでGPS情報を扱う Geokit というgemがある。これは Google や Yahoo などと連携する機能も提供しているが、その中に2点間の距離を求める distance_to というメソッドがある。このソースコードを調査した上で、採用されている理論を調査した。
角度の単位
緯度と経度は球体(地球)中心からの角度である。一般的に角度の単位は1周を360とする 60分法 で記述されるが、当記事では円弧の長さを扱うため、1周を $2 \pi$ とする ラジアン を用いる。なお、60分法からラジアンへは $\pi / 180$ 倍、逆にラジアンから60分法へは $180 / \pi$ 倍すれば変換できる。
計算上の留意点
地球は正確には球面ではなく楕円体である。楕円状の2点間の距離を求める方法も存在する (国土地理院による解説) が、非常に複雑であるため計算上あまり利用されていない様子。ここでは地球を完全な球体であると近似する。なお、以降地球の半径を $R$ で表し、その値は正確に $R = 6378137 [m]$ である。
計算方法紹介
前提
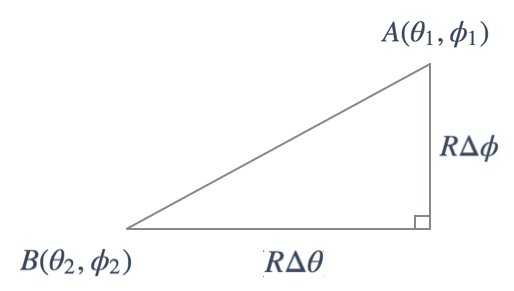
緯度と経度が分かっている2点 $A(\theta_1, \phi_1), B(\theta_2, \phi_2)$ の球面上の最短距離$D$ を求める ( 大円距離 という) 。また、2点の緯度の差を $\Delta\theta = |\theta_2 - \theta_1|$, 経度の差を $\Delta\phi = |\phi_2 - \phi_1|$ で表す。
近似計算
2点間が近い場合は、平面上の計算で近似できる。多分日本国内くらいの距離感であればそこそこ正確な値が出る。以下の図を見ると、ピタゴラスの定理により導出できることが分かる。
式は以下のとおり。
\begin{align*}
D & = \sqrt{(R\Delta\theta)^2 + (R\Delta\phi)^2} \\
& = R\sqrt{\Delta\theta^2 + \Delta\phi^2}
\end{align*}
球面距離計算
2点間が離れていると、上記の方法では正確な値にならない。ここでは球面三角法の定理を用いて2点間の距離を正確に求める方法を紹介する。
基本となる計算手順
2点間の距離とは、2点 $A, B$ と地球の中心 $O$ を通る平面と地球の断面が作る円 (これが大円である) における円弧の長さである。地球の半径は分かっているので、あとは 中心角 $\angle AOB$ が分かればよい。以下、これを $x$ とする。
球面三角法の余弦定理
球面上の三角形が成す角度の関係を表す定理。以下 Wikipedia から引用する。なお、球面上の「辺」とは「2点と球の中心が成す中心角」であり、実際の長さはこれに球の半径を乗じることで算出する。
$ABC$ を球面三角形とし辺 $BC, CA, AB$ をそれぞれ $a, b, c$ とする。弧 $AB$ を含む大円と弧 $AC$ を含む大円がなす角を $A$ 、同様に $B, C$ も決定する。そのとき、次の式が成り立つ。
\begin{align*}
\cos a & = \cos b \cos c + \sin b \sin c \cos A \\
\cos b & = \cos c \cos a + \sin c \sin a \cos B \\
\cos c & = \cos a \cos b + \sin a \sin b \cos C
\end{align*}
(この定理の導出までは踏み込みません…Wikipediaの上記記事を参照してください)
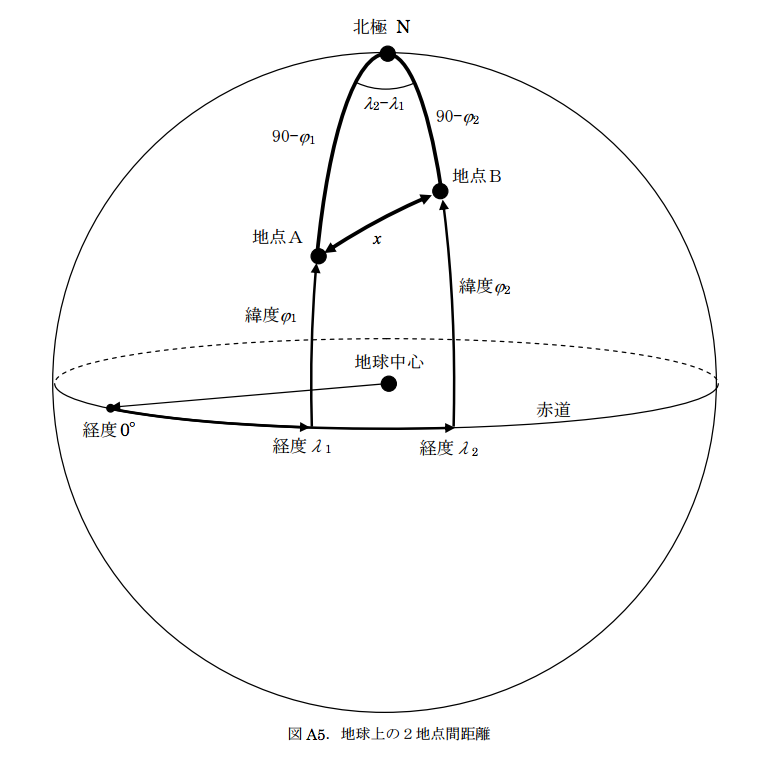
ここで上記の第3式において、 $A, B$ を距離を求めたい2点、 $C$ として北極 $N = (\pi / 2, 0)$ を取る。図は以下の通り (山口大学のサイト より引用)。
この時、以下の事実が成り立つ。
- 角 $c$ は円弧 $A, B$ を通る大円の角となり、これが求める中心角 $x$ である。
- 角 $C$ は「北極・点$A$を含む大円と北極・点$B$を通る大円が成す角」すなわち2点の経度の差 $\Delta\phi$ となる。
- 角 $a$ は北極と点 $A$ が成す中心角なので $a = \frac{\pi}{2} - \theta_1$
- 同様に $b = \frac{\pi}{2} - \theta_2$
以上の事実を球面余弦定理に当てはめると
\begin{align*}
\cos x & = \cos (\frac{\pi}{2} - \theta_1) \cos (\frac{\pi}{2} - \theta_2) + \sin (\frac{\pi}{2} - \theta_1) \sin (\frac{\pi}{2} - \theta_2) \cos \Delta\phi \\
& = \sin \theta_1 \sin \theta_2 + \cos \theta_1 \cos \theta_2 \cos (\phi_2 - \phi_1)
\end{align*}
すなわち
x = \cos^{-1} (\sin \theta_1 \sin \theta_2 + \cos \theta_1 \cos \theta_2 \cos (\phi_2 - \phi_1))
となり、2点間の緯度と経度のみから中心角を得ることができた。距離を求めるためには、上記の中心角に半径を掛ければよい。
D = Rx = R \cos^{-1} (\sin \theta_1 \sin \theta_2 + \cos \theta_1 \cos \theta_2 \cos (\phi_2 - \phi_1))
Geokit による距離の計算
Geokit では上記2通りの計算方法を提供している。値が正確なのはもちろん球面計算だが、計算が単純である平面近似の方がパフォーマンスが良い、と推測される。サービスの特徴によって使い分けるべきであろう。
例: 近郊区間
東京駅から新宿駅への距離を geokit で求める。Google Geocoder APIは施設名を入力すると対応する位置情報を取得できるので、以下の雑なコードで計算が可能。平面近似と球面計算の両方を試す。
なお、 Geokit::default_units = :kms を書かないと、距離の単位が マイル になってしまう。日本人にはやや不親切な仕様である。
require 'geokit'
include Geokit::Geocoders
Geokit::default_units = :kms
shinjuku_sta = GoogleGeocoder.geocode('新宿駅')
tokyo_sta = GoogleGeocoder.geocode('東京駅')
puts shinjuku_sta.distance_to(tokyo_sta, formula: :flat)
puts shinjuku_sta.distance_to(tokyo_sta, formula: :sphere)
$ ruby distance.rb
6.113488210245911
6.114010007364786
平面の方が0.5mほど短く算出されることが分かる。1
例: 国内線航路
那覇空港(沖縄)から新千歳空港(北海道)への距離を同様にして求める。コード例は似ているので省略する。
$ ruby distance.rb
2315.5289534458057
2243.0914637502415
距離の誤差が70km以上にまで広がっている。海を越える場合は平面近似を使うべきでないだろう。
例: 国際線航路
成田空港(日本)からヒースロー空港(イギリス)までの距離は以下の通り2。カタカナでも使えるんだ…
require 'geokit'
include Geokit::Geocoders
Geokit::default_units = :kms
p1 = GoogleGeocoder.geocode('成田空港')
p2 = GoogleGeocoder.geocode('ヒースロー空港')
puts p1.distance_to(p2, formula: :sphere)
$ ruby distance.rb
9599.496116222344
おわりに
盛り込まなかったこと
- 球面上の余弦定理の導出
- 平面・球面計算のベンチマーク
まとめ
Rubyで位置情報を扱うための方法と、その背後にある幾何学の理論を紹介した。普段の仕事ではツールやソースコードに注目しがちだが、その背後にある理論に注目することで、より応用の幅が広がるだろう。