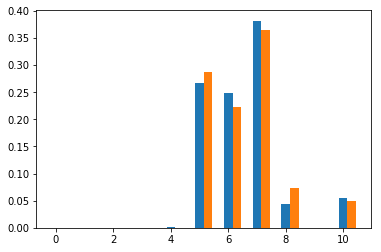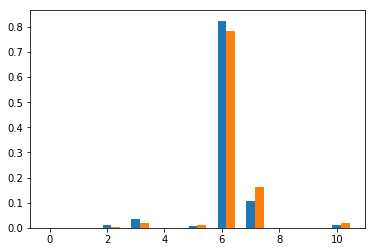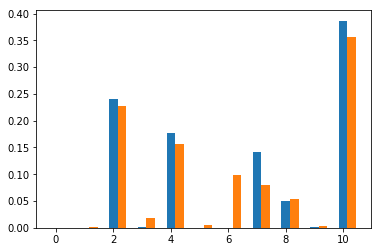逐次転移過程のシミュレーションとニューラルネットワークによる長時間後の状態学習・予測

行うこと

① でこぼこな山谷を行き来する多数粒子の状態遷移のモンテカルロシミュレーション
② 山谷の状態(極小値、極大値)と温度から長時間経過後の状態(各状態にある粒子の割合)をニューラルネットで予測できるか

①多数粒子の状態遷移のモンテカルロシミュレーション

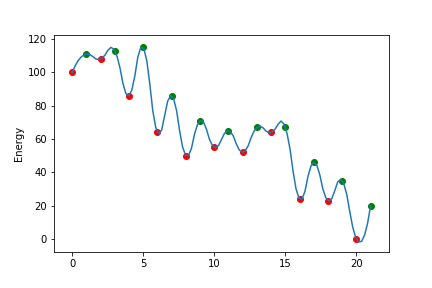
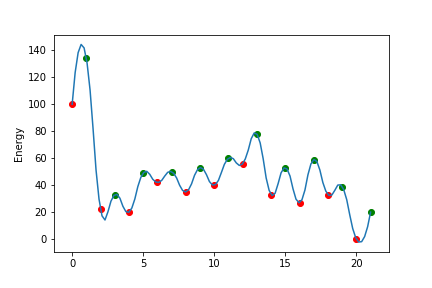
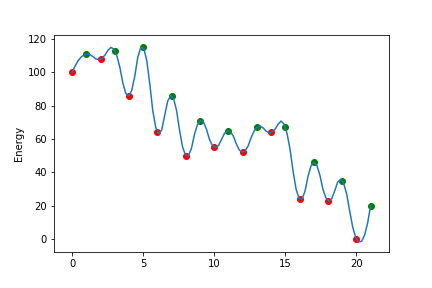
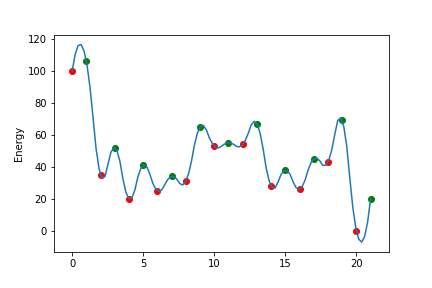
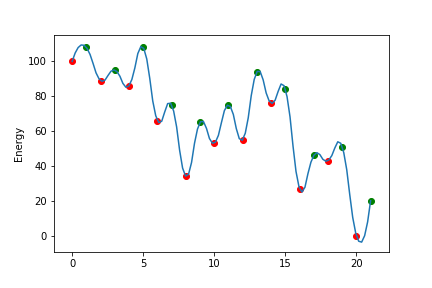
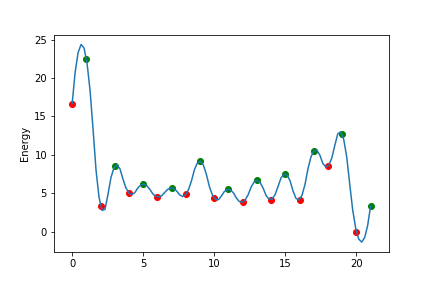
上の図のようなエネルギー曲線があると考え、粒子は極小値minima(赤丸)の位置しかいることができないとする。
極小値(赤丸)のエネルギーを左から$minimaE[0]$、$minimaE[1]$...、極大値(緑丸)のエネルギーを左から$maximaE[0]$、$maximaE[1]$...、
極小値に対応した物理量を左から$Q[0]=10, Q[1]=9,...Q[10]=0$とする。

粒子は熱攪乱により左右に行き来し、
左右を隔てる山の高さを$\Delta E$(それぞれ$\Delta E_{left}=E_{左の緑丸の極大値}-E_{赤丸}、\Delta E_{right}=E_{右の緑丸の極大値}-E_{赤丸}$)とすると粒子が山を乗り越える確率を$e^{\frac{-ΔE}{T}}$とする。
($T$は温度。温度が山に対して相対的に高くなるほど左右に移る確率は高くなる。今回は定温で6に設定。）

左右移る/その場にいるしか選択肢がないため、三重対角行列の遷移確率行列をもったマルコフ連鎖のシミュレーションと同じ感じと思われる。

以下のアルゴリズムでシミュレーションを実施

1. 粒子は100個とし、最初は全て一番左の赤丸の位置($E_{minima}[0]$)に設定。
2. エネルギー極大値、極小値をランダムに以下手順で設定する。
   1. 左右端の極小値を固定(100と0)
   2. 左から、極小値iに2～40のランダム値を足したものを右隣の極大値iとする。
   3. 一番右の極小値+20～極大値iの間のランダムな値を右隣の極小値i+1とする。
   4. 2と3を右に行くまで繰り返す。
3. 各粒子に対して以下を行う。
   1. 左か右か0.5の確率で遷移方向候補を選択
   2. 上記の乗り越える確率で遷移を決定
4. NUM_ITER(100000)回3を繰り返す。
5. シミュレーション回数分1～4を繰り返す。

観測される物理量は、各状態にいる粒子の割合×各状態の物理量を全ての状態で和をとった値となる。
$\sum_{i}Q[i]×\frac{minimaE[i]にある粒子数}{全粒子数}$

①のソース

import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import interp1d
from datetime import datetime as dt
import os
import tensorflow as tf
%matplotlib inline

class SuccessiveTransitionSimulator:

    def __init__(self, init_minima_E, init_delta_E, Q, NUM_ITER=20000, NUM_PARTICLE = 100, temperature=6):
        self.NUM_PARTICLE = NUM_PARTICLE  # 粒子の数
        self.NUM_ITER = NUM_ITER  # イテレーション回数
        self.minima_E = init_minima_E  # 各エネルギー極小値
        self.delta_E = init_delta_E  # 各極小値のを隔てるエネルギー壁の高さ
        self.maxima_E = self.minima_E + self.delta_E  # 各エネルギー極大値
        self.Q = Q  # 各エネルギー極小値状態に対応する物理量
        self.particles_pos = np.zeros(self.NUM_PARTICLE)  # 各粒子の位置。0(一番左の極小値)で初期化。
        self.temperature = temperature  # 温度
        self.rates_history = []  # 各状態にある粒子の割合(rates[i]=極小値iにいる粒子数/全粒子数)の時系列
        self.q_history = []
        self.P_DIR = dt.now().strftime('%Y_%m_%d_%H_%M_%S')

    def set_temperature(self, temperature):
        self.temperature = temperature

    def get_temperature(self):
        return self.temperature

    def simulate(self, save_fig=True):
        for _ in range(self.NUM_ITER):

            for i, particle_pos in enumerate(self.particles_pos):
                left_p = 0  # 左に移る確率
                right_p = 0  # 右に移る確率

                rand = np.random.rand()

                # 遷移方向(右/左)をランダムに決める
                if np.random.rand() < 0.5:
                    # 一番左にいる場合は何もしない
                    if particle_pos > 0:
                        # 左に移る確率を計算
                        left_p = np.exp(-max(0, self.maxima_E[int(particle_pos-1)] - self.minima_E[int(particle_pos)])/self.temperature) / self.temperature
                        # left_pの確率で左に移る
                        if left_p > rand:
                            self.particles_pos[i] -= 1
                else:
                    # 一番右にいる場合は何もしない
                    if particle_pos < len(self.minima_E)-1:
                        # 右に移る確率を計算
                        right_p = np.exp(-max(0, self.maxima_E[int(particle_pos)] - self.minima_E[int(particle_pos)])/self.temperature) / self.temperature
                        # right_pの確率で右に移る
                        if right_p > rand:
                            self.particles_pos[i] += 1

            # 各準安定状態にある粒子の割合ratesと全体として観測される物理量qを計算
            q = 0
            rates = []
            for j in range(len(self.minima_E)):
                rate = len(*np.where(self.particles_pos == j)) / self.NUM_PARTICLE
                q += self.Q[j] * rate
                rates.append(rate)
            self.rates_history.append(rates)
            self.q_history.append(q)

        if save_fig:
            self._save_fig()


    def _save_fig(self):
        out_dir = 'Transition/{}/{}'.format(self.P_DIR, dt.now().strftime('%Y_%m_%d_%H_%M_%S'))
        if not os.path.exists(out_dir):
            os.makedirs(out_dir)

        # 極小値、極大値、補間した曲線をプロット
        plt.subplots(1, 1)
        points = []
        for minima, maxima in zip(self.minima_E, self.maxima_E):
            points.append(minima)
            points.append(maxima)
        interpolate = interp1d([i for i in range(len(points))], points, kind='quadratic')
        xlist = np.linspace(0, len(points)-1, num=101)
        plt.ylabel("Energy")
        plt.plot(xlist, interpolate(xlist))
        plt.scatter([2*x for x in range(len(self.minima_E))], self.minima_E, color='red')
        plt.scatter([2*x+1 for x in range(len(self.maxima_E))], self.maxima_E, color='green')
        plt.savefig(out_dir + '/energy_curve.png')

        # 観測される物理量の時系列変化をプロット 
        plt.subplots(1, 1)
        plt.ylim(-0.1, 10.1)
        plt.xlabel("Iteration")
        plt.ylabel("Physical Quantity")
        plt.plot([x for x in range(len(self.q_history))], self.q_history)
        plt.savefig(out_dir + '/q-t_curve.png')

        # 各状態の粒子の割合の時系列変化をプロット
        self.rates_history = np.array(self.rates_history)
        plt.subplots(1, 1)
        plt.ylim(-0.1, 1.1)
        plt.xlabel("Iteration")
        plt.ylabel("Particle Rate")
        for k in range(len(self.Q)):
            plt.plot(self.rates_history[:, k], label='State {}'.format(k))
        plt.legend()
        plt.savefig(out_dir + '/rates-t_curve.png')

        # 各状態の粒子の割合最終状態を棒グラフでプロット
        plt.subplots(1, 1)
        plt.ylim(-0.1, 1.1)
        plt.xlabel("State")
        plt.ylabel("Particle Rate")
        plt.bar([i for i in range(len(self.rates_history[-1, :]))], self.rates_history[-1, :])
        plt.savefig(out_dir + '/final_rates.png')


    # エネルギー壁をランダムに初期化、粒子の位置を0で初期化
    def random_init(self):
        # 極小値、極大値をランダム値で初期化する。※両端の極小値は固定
        self.delta_E = np.random.randint(2, 40, len(self.delta_E))
        for i in range(len(self.delta_E)-2):
            self.maxima_E[i] = self.minima_E[i] + self.delta_E[i]
            self.minima_E[i+1] = np.random.randint(self.minima_E[-1] + 20, self.maxima_E[i], 1)
        self.maxima_E[len(self.delta_E)-2] = self.minima_E[len(self.delta_E)-2] + self.delta_E[len(self.delta_E)-2]

        # 粒子の位置を初期化
        self.particles_pos = np.zeros(self.NUM_PARTICLE)
        self.particles_pos[:] = 0
        self.q_history = []
        self.rates_history = []


    # エネルギー極値を左から並べたリストを取得
    def get_extremes(self):
        extrems = []
        for minima, maxima in zip(self.minima_E, self.maxima_E):
            extrems.append(minima)
            extrems.append(maxima)
        return np.array(extrems)

    # 各状態の粒子の割合の時系列データを取得
    def get_rates_history(self):
        return np.array(self.rates_history)

    # 各粒子の位置を取得
    def get_particles_pos(self):
        return self.particles_pos

if __name__ == '__main__':
    sts = SuccessiveTransitionSimulator(
        init_minima_E=np.array([100, 90, 80, 70, 60, 50, 40, 30, 20, 10 , 0]), # エネルギー極小値初期状態
        init_delta_E=np.array([20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20]),
        Q=np.array([10, 9, 8, 7, 6, 5, 4, 3, 2, 1, 0]), # エネルギー極小値に対応した物理量
        NUM_ITER=100000
    )

    DATA_LEN = len(sts.get_extremes())

    extremes_series = []
    rates_series = []

    temperature = sts.get_temperature()

    # 200回シミュレーションを回す
    for _ in range(200):
        print(_)
        sts.simulate(save_fig=True)
        extremes = sts.get_extremes()
        extremes_series.append(extremes/temperature)
        rates_history = sts.get_rates_history()
        rates_series.append(np.mean(rates_history[-100:, :], axis=0))  # 割合変化はぶれが大きい場合があるため、最後から100個のデータの平均を最終状態とする。
        print(sts.get_particles_pos())
        sts.random_init()

結果

初回

• エネルギー曲線(手動設定)

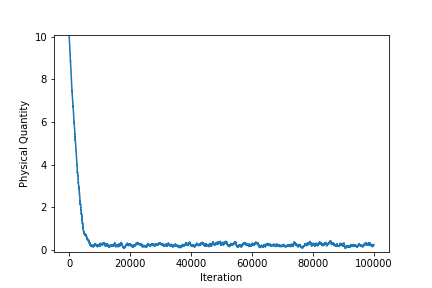
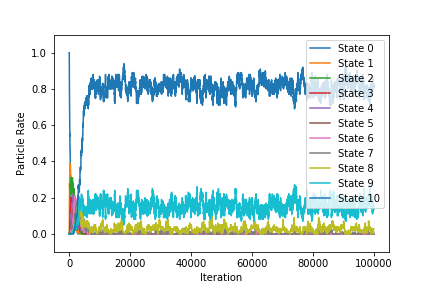
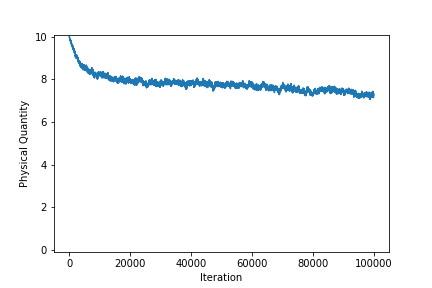
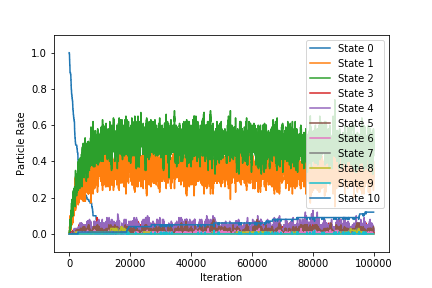
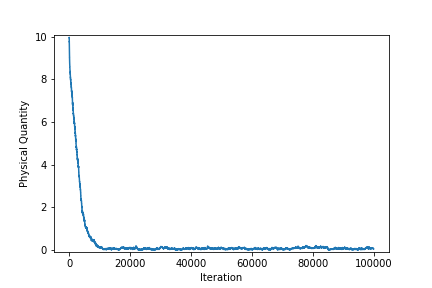
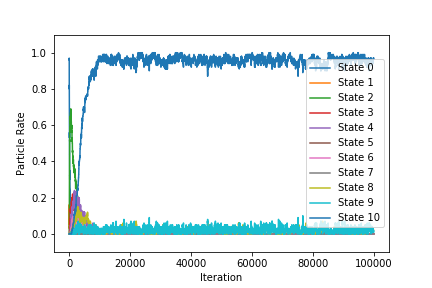
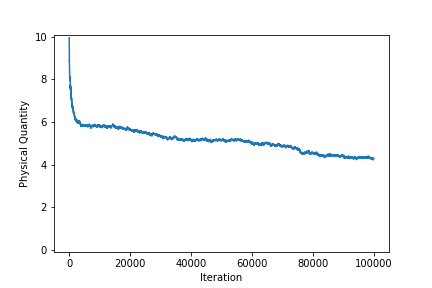
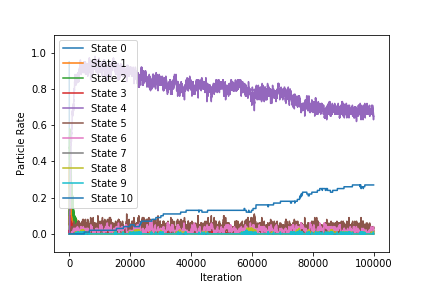
• 観測される物理量と各状態の粒子割合の時間変化

階段状にしたので一番右の安定状態へすぐに遷移している。

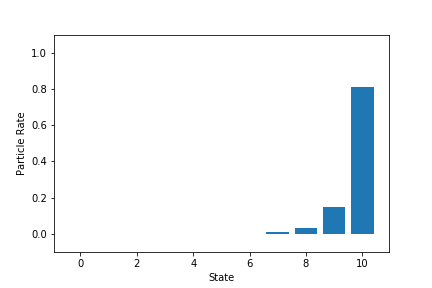
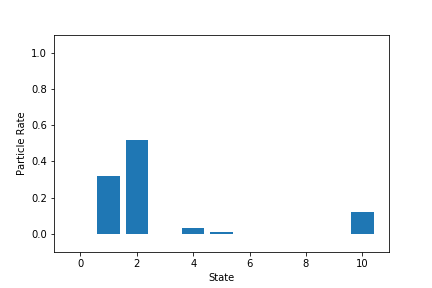
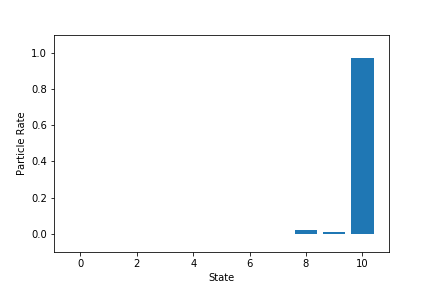
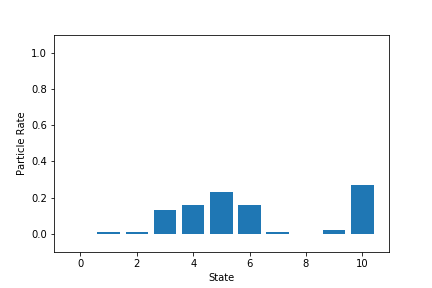
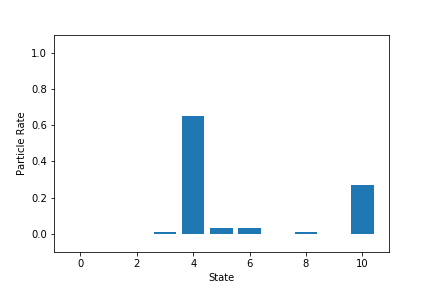
• 各状態の粒子割合の最終状態

---

2回目

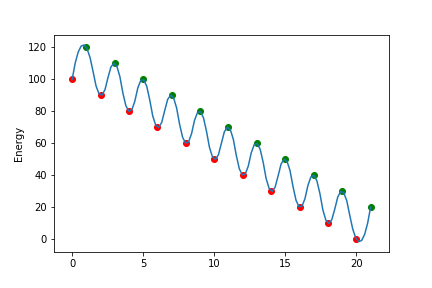
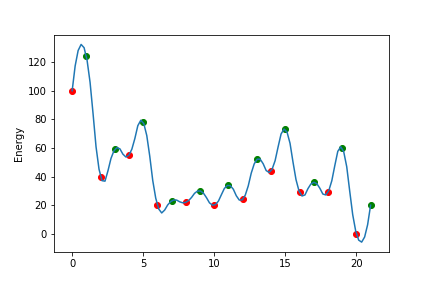
• エネルギー曲線

• 観測される物理量と各状態の粒子割合の時間変化

状態1,2あたりの谷にトラップされている。

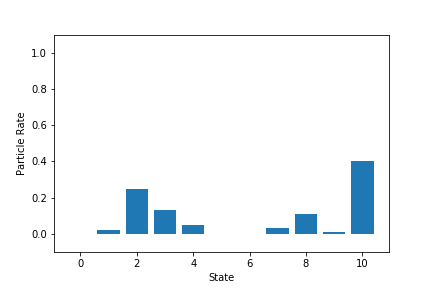
• 各状態の粒子割合の最終状態

3回目

• エネルギー曲線

• 観測される物理量と各状態の粒子割合の時間変化

• 各状態の粒子割合の最終状態

4回目

• エネルギー曲線

• 観測される物理量と各状態の粒子割合の時間変化

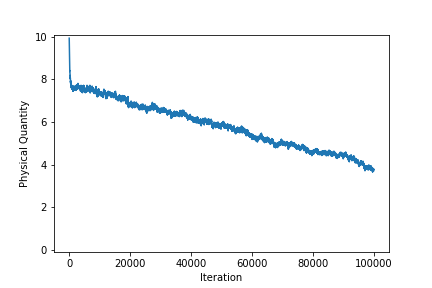
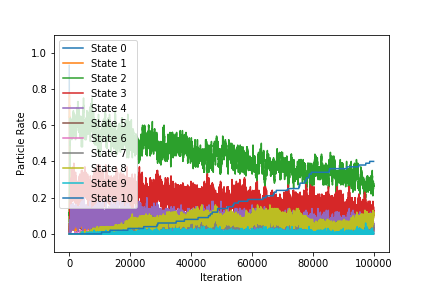
状態2,3あたりにトラップされているが、徐々に安定状態へ遷移していっている。

• 各状態の粒子割合の最終状態

5回目

• エネルギー曲線

• 観測される物理量と各状態の粒子割合の時間変化

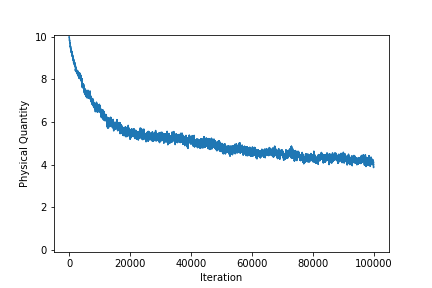
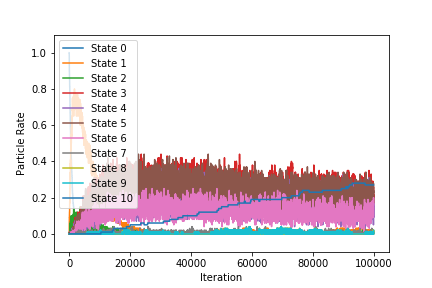
状態3,4,5あたりでトラップ。隔てるエネルギー壁が小さいためぶれがでかい。

• 各状態の粒子割合の最終状態

6回目

• エネルギー曲線

• 観測される物理量と各状態の粒子割合の時間変化

• 各状態の粒子割合の最終状態

②ニューラルネットワーク(NN)による長時間後の状態学習・予測

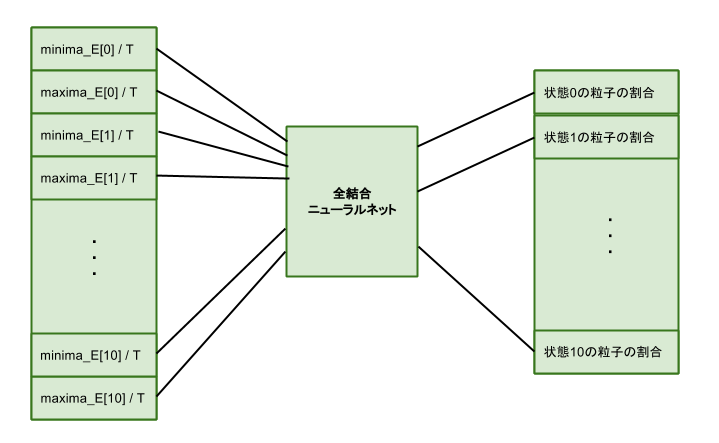
上記のシミュレーションを400回繰り返し、入力をエネルギー極値(極小値、極大値を左から並べた値)/温度、出力を最終状態(100000イテレーション後)の粒子の各状態の割合(Particle Rate)として全結合ニューラルネットに学習させる。

イメージとしては↓

学習後、ランダムに初期化した状態をNNに入力し最終状態の各粒子割合の予測する。また、実際にシミュレーションを走らせ、結果を予測結果と比較する。

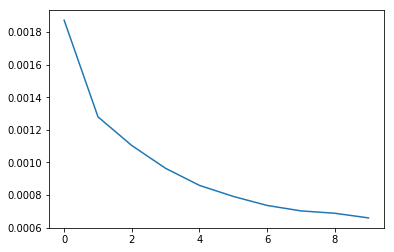
学習結果

• 損失
  

• 学習データでの予測粒子割合と、実際のシミュレーションでの最終粒子割合(いくつか抜粋)
  

ある程度学習はできている模様。

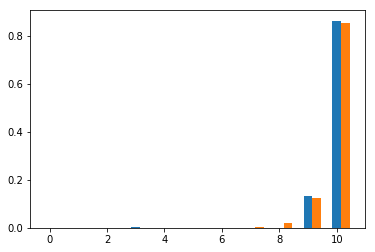
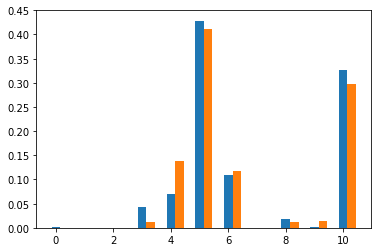
実学習データでの予測結果(いくつか抜粋)

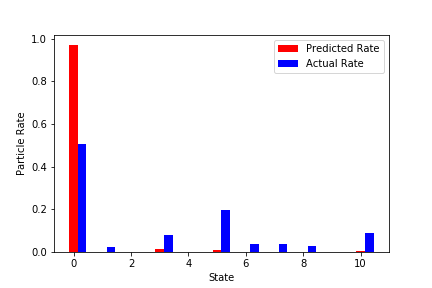
赤が学習済みNNから予測した粒子の最終状態。
青が実際のシミュレーションでの最終状態。

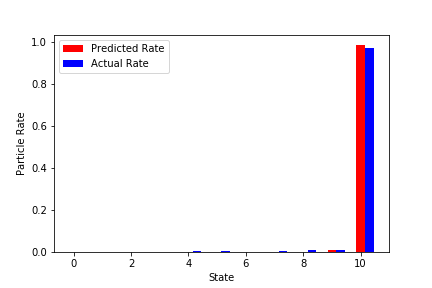
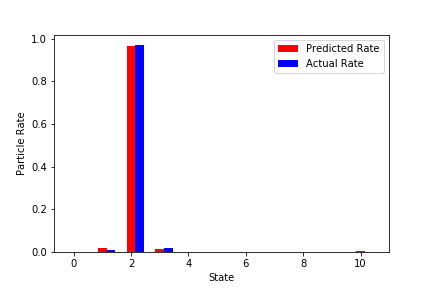
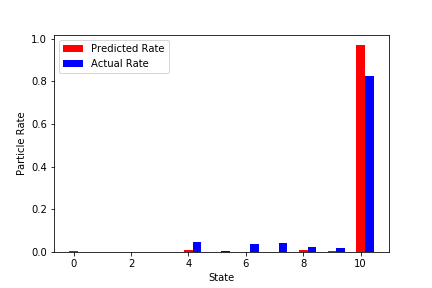
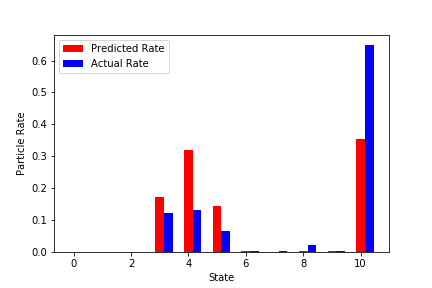
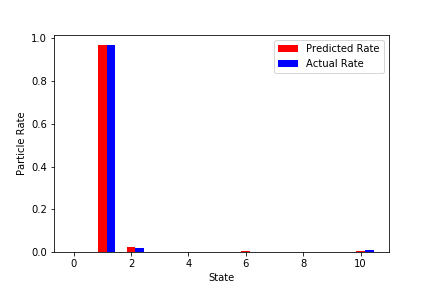
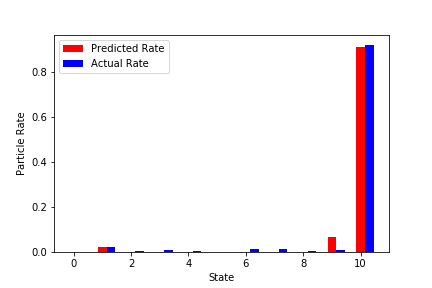
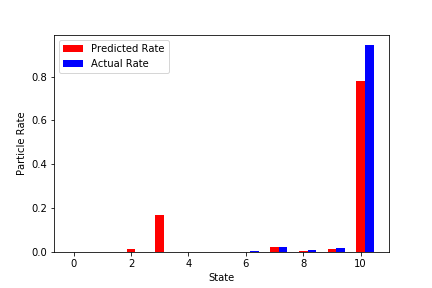
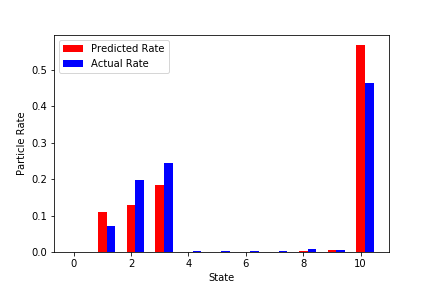
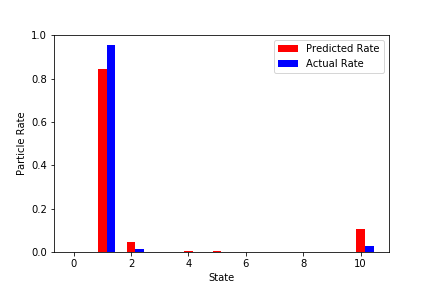
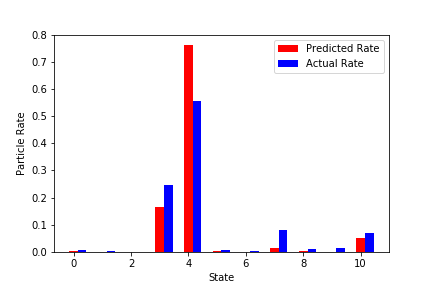
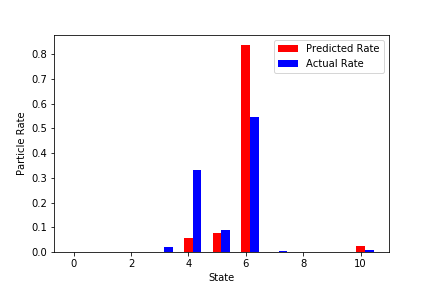
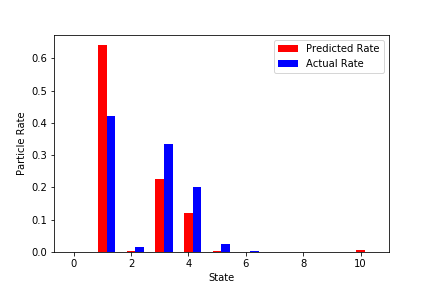
↓結構外れているものを抜粋

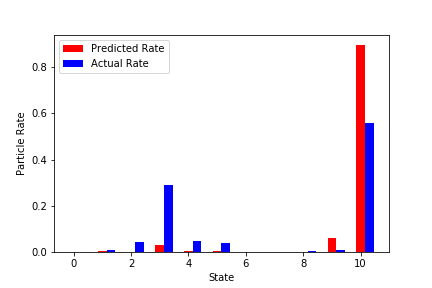
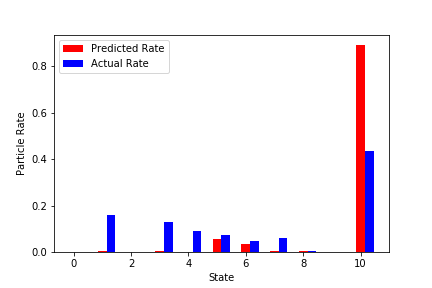
100000回学習済みNNから予測を行い、粒子の割合が均等になるようなエネルギー曲線を推測

100000回状態の初期化、その時のエネルギー極値から学習済みNNで予測を行い、予測結果の粒子の割合の分散が一番小さい割合をBest Rates、そのときのエネルギー極値をBest Extremsとする。

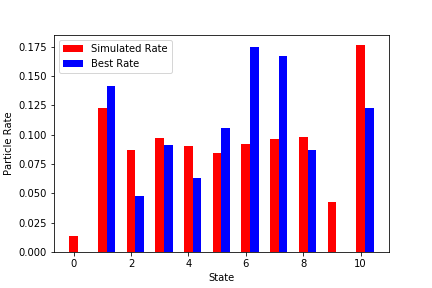
Best Ratesをプロットすると

均等ではないが、ある程度まばらに割合にはなっている。

また、この時のエネルギー曲線(Best Extremes)をプロットしてみると

安定、一番不安定(一番左)に移らずに間でトラップされるような構造にはなっている感じはする。

②のソース

NNモデル

class FCNN1DRegressionModel:
    """
    1次元全結合ニューラルネットワーク
    """
    def __init__(self, input_size, output_size):
        # 入力
        self.input_x = tf.placeholder(tf.float32, [None, input_size])

        # 入力層
        W_fc1 = tf.Variable(tf.truncated_normal([input_size, 64], stddev=0.01))
        b_fc1 = tf.Variable(tf.zeros([64]))
        h_fc1 = tf.nn.relu(tf.matmul(self.input_x, W_fc1) + b_fc1)

        # 出力層
        W_out = tf.Variable(tf.truncated_normal([64, output_size], stddev=0.01))
        b_out = tf.Variable(tf.zeros([output_size]))
        self.y = tf.matmul(h_fc1, W_out) + b_out
        self.scores = tf.nn.softmax(self.y)

        # 損失関数
        self.input_y = tf.placeholder(tf.float32, [None, output_size])
        self.loss = tf.reduce_mean(tf.square(self.input_y - self.scores))

400回シミュレーション ⇒ NNで学習 ⇒ 実学習データで精度検証 ⇒ 粒子割合が均等になるようなエネルギー極値予測

if __name__ == '__main__':
    sts = SuccessiveTransitionSimulator(
        init_minima_E=np.array([100, 90, 80, 70, 60, 50, 40, 30, 20, 10 , 0]), # エネルギー極小値初期状態
        init_delta_E=np.array([20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20]),
        Q=np.array([10, 9, 8, 7, 6, 5, 4, 3, 2, 1, 0]),
        NUM_ITER=100000
    )

    DATA_LEN = len(sts.get_extremes())

    extremes_series = []
    rates_series = []

    temperature = sts.get_temperature()

    # 400回シミュレーションを実施
    for _ in range(400):
        print(_)
        sts.simulate(save_fig=True)
        extremes = sts.get_extremes()
        extremes_series.append(extremes/temperature)
        rates_history = sts.get_rates_history()
        rates_series.append(np.mean(rates_history[-20:, :], axis=0))
        print(sts.get_particles_pos())
        sts.random_init()


    train_output = np.array(rates_series)
    train_input = []
    for extremes in extremes_series:
        train_input.append([[extreme] for extreme in extremes])
    train_input = np.array(train_input).reshape(-1, DATA_LEN)
    print(train_output)
    print(train_input)

    INPUT_DATA_LEN = len(train_input[0]) # データ長
    print(INPUT_DATA_LEN)
    INPUT_DATA_NUM = len(train_input) # データ数
    print(INPUT_DATA_NUM)
    DIM_OUTPUT = len(train_output[0]) # 出力層次元
    print(DIM_OUTPUT)

    sess = tf.InteractiveSession()
    sess.run(tf.global_variables_initializer())

    model = NN1DRegressionModel(input_size=INPUT_DATA_LEN, output_size=DIM_OUTPUT)

    global_step = tf.Variable(0, name="global_step", trainable=False)
    optimizer = tf.train.AdamOptimizer(1e-3)
    grads_and_vars = optimizer.compute_gradients(model.loss)
    train_op = optimizer.apply_gradients(grads_and_vars, global_step=global_step)

    sess.run(tf.global_variables_initializer())

    TRAIN_STEPS = 30000

    loss_history = []
    # ↑でシミュレーションした結果を全結合ニューラルネットで学習開始
    print("Started Training..")
    local_step = 0
    while True:
        local_step += 1

        x_batch = train_input
        y_batch = train_output
        feed_dict = {
          model.input_x: x_batch,
          model.input_y: y_batch,
        }
        _, step, loss, scores = sess.run(
            [train_op, global_step, model.loss, model.scores],
            feed_dict)

        if step % 3000 == 0:
            print('Step:{}, loss:{}'.format(step, loss))
            print('Step:{}, scores:{}'.format(step, scores))
            loss_history.append(loss)

        if step >= TRAIN_STEPS:
            break

    # 損失の変化をプロット
    plt.subplots(1, 1)
    plt.plot(loss_history)
    # 学習データでの予測粒子割合と、実際のシミュレーションでの最終粒子割合をプロット
    for score, out in zip(scores, train_output):
        plt.subplots(1, 1)
        plt.bar([i for i in range(len(score))], score, width=0.3, align="center")
        plt.bar([i+0.3 for i in range(len(score))], out, width=0.3, align="center")


    # 予測精度検証用シミュレーション
    for _ in range(10):
        sts.simulate(save_fig=False)
        extremes = sts.get_extremes() / temperature

        rates_history = sts.get_rates_history()
        final_rates = np.mean(rates_history[-20:, :], axis=0)

        predicted_scores = sess.run([model.scores], {model.input_x: np.array([[extreme] for extreme in extremes]).reshape(1, DATA_LEN)})
        print('predicted_scores : ', predicted_scores)

        plt.subplots(1, 1)
        plt.bar([i for i in range(len(predicted_scores[0][0]))], predicted_scores[0][0], width=0.3, align="center", color='red', label='Predicted Rate')
        plt.bar([i+0.3 for i in range(len(final_rates))], final_rates, width=0.3, align="center", color='blue', label='Actual Rate')
        plt.xlabel("State")
        plt.ylabel("Particle Rate")
        plt.legend()
        plt.savefig('Transition/predicted_rate{}.png'.format(_))

        sts.random_init()

    # 粒子均等割り合となるエネルギー極値予測シミュレーション
    var = 10000000
    best_extremes = []
    best_scores = []
    for _ in range(100000):
        sts.random_init()
        extremes = sts.get_extremes() / temperature
        predicted_scores = sess.run([model.scores], {model.input_x: np.array([[extreme] for extreme in extremes]).reshape(1, DATA_LEN)})
        if var > np.var(predicted_scores[0][0]):
            var = np.var(predicted_scores[0][0])
            best_scores = predicted_scores[0][0]
            best_extremes = sts.get_extremes().copy() / temperature

    print('best scores : ', best_scores)
    print('best extremes : ', best_extremes)
    sts.set_extremes(best_extremes)
    sts.simulate(save_fig=True)
    rates_history = sts.get_rates_history()
    simulated_final_rates = np.mean(rates_history[-20:, :], axis=0)

    plt.subplots(1, 1)
    plt.bar([i for i in range(len(simulated_final_rates))], simulated_final_rates, width=0.3, align="center", color='red', label='Simulated Rate')
    plt.bar([i+0.3 for i in range(len(best_scores))], best_scores, width=0.3, align="center", color='blue', label='Best Rate')
    plt.xlabel("State")
    plt.ylabel("Particle Rate")
    plt.legend()
    plt.savefig('Transition/predicted_and_best_rate.png')

まとめ

逐次転移のシミュレーションに無理やりNNを応用してみたが、とりわけ精度が高く予測できたわけでもなく、どのようなエネルギー曲線が安定状態へ移りやすい/移りにくいか直観的にも大体予想できるため、NNネタとしてはあまり面白くなかったかもしれない。。