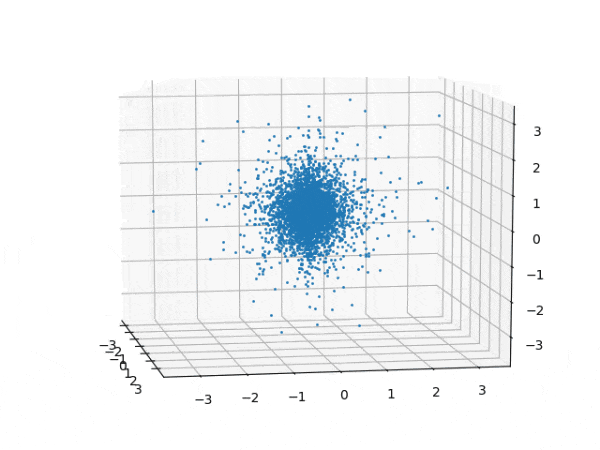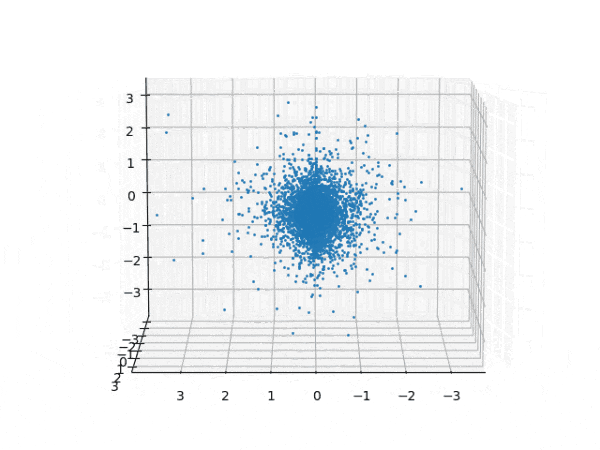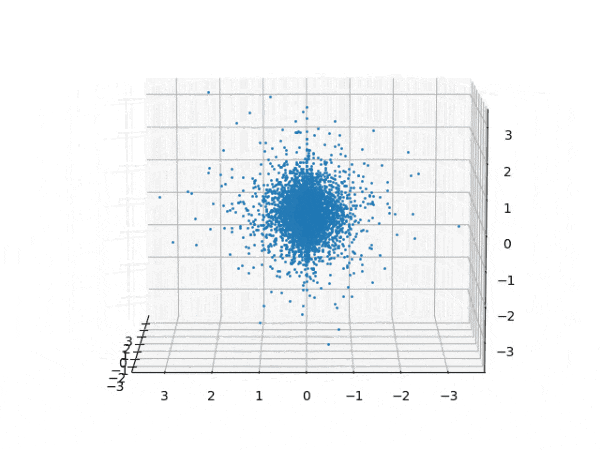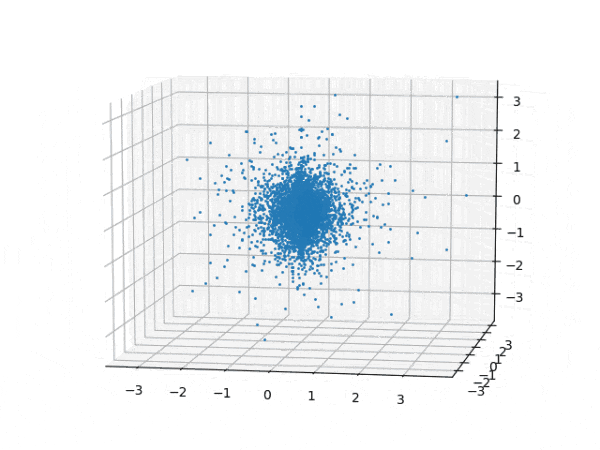
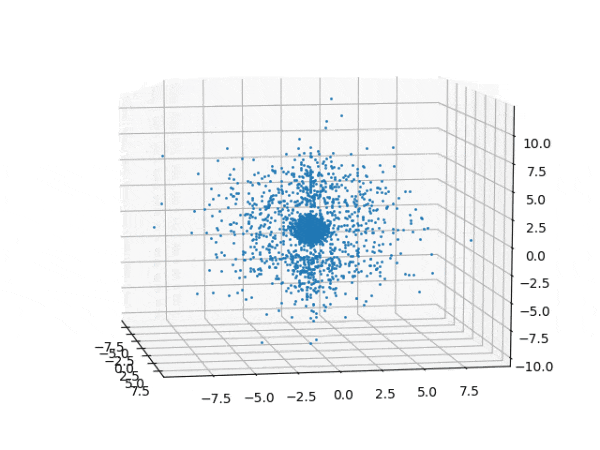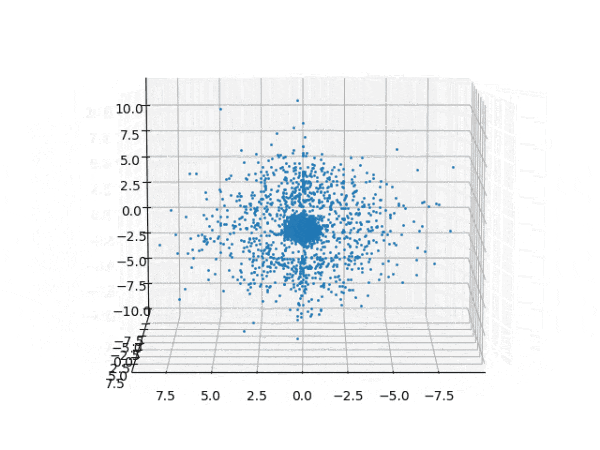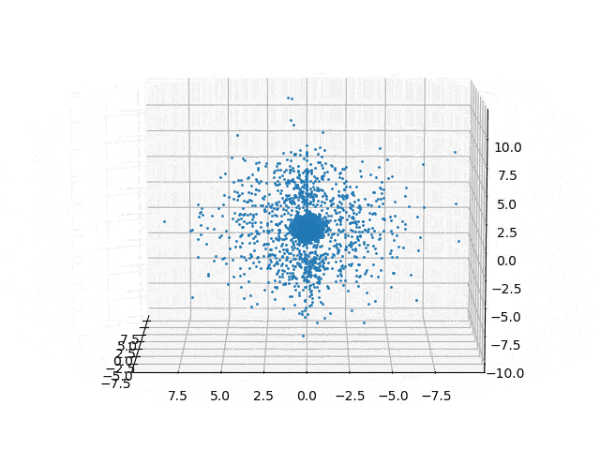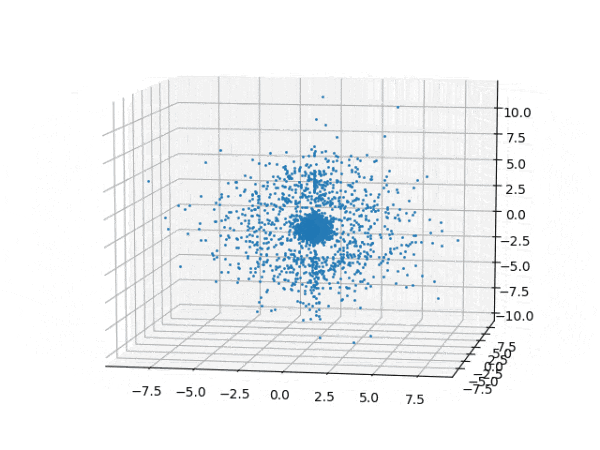
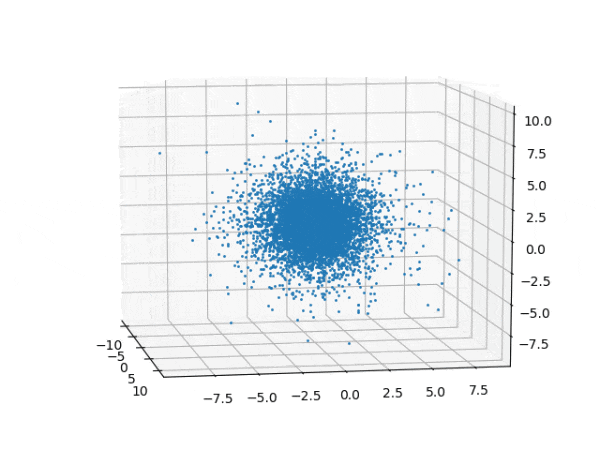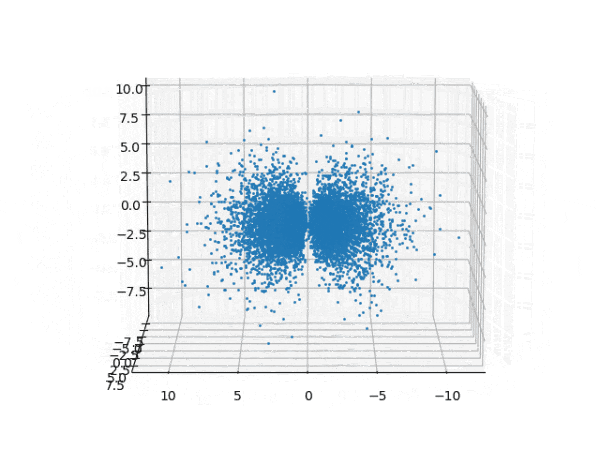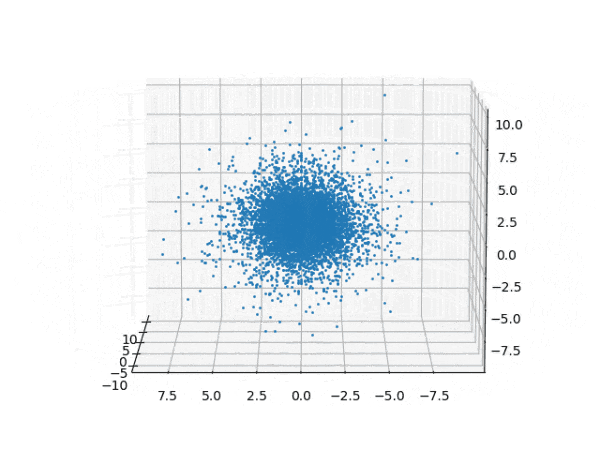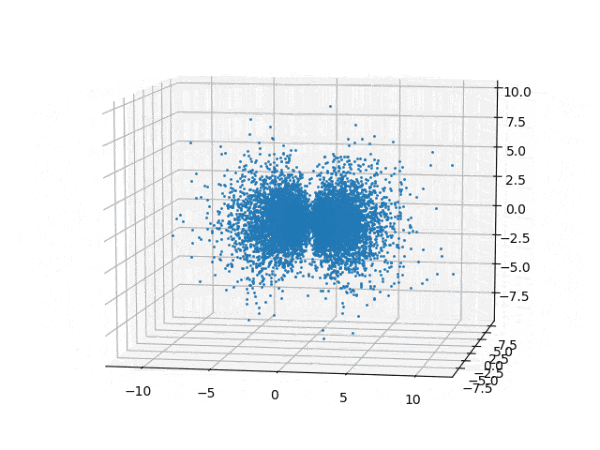
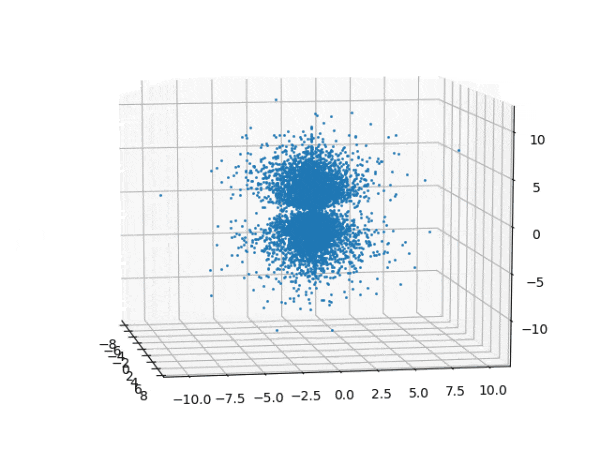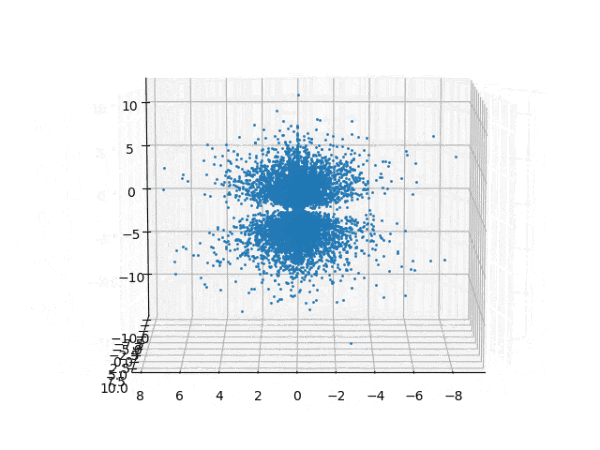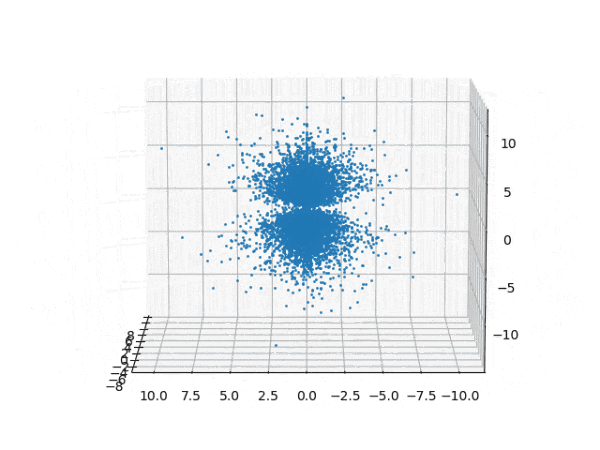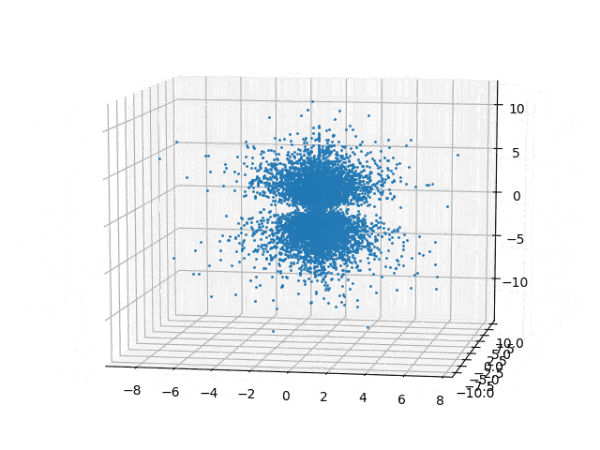
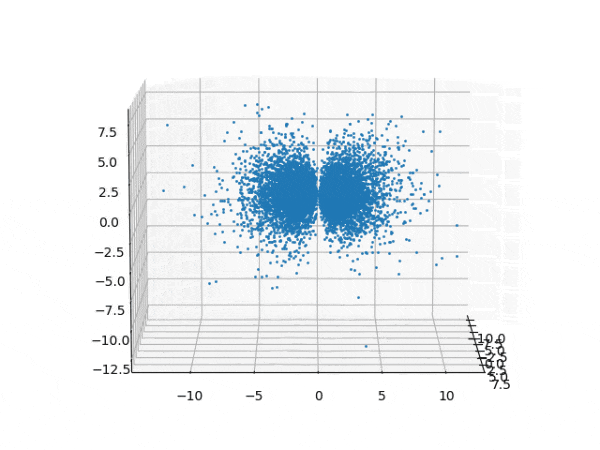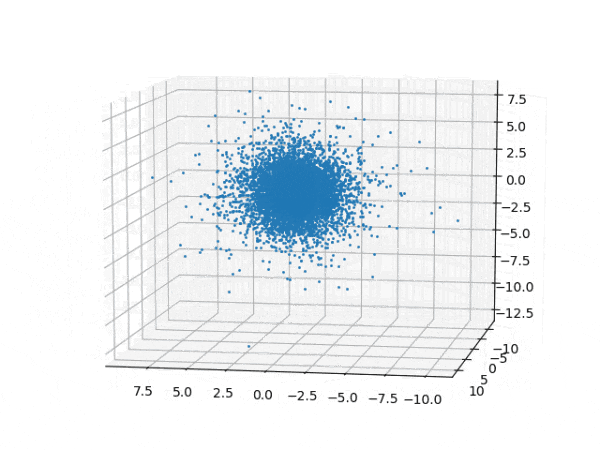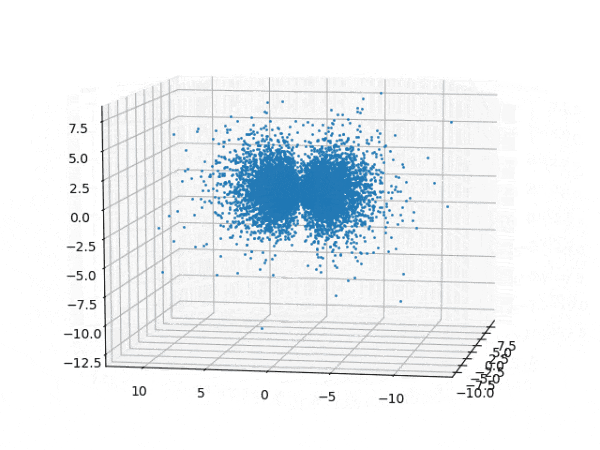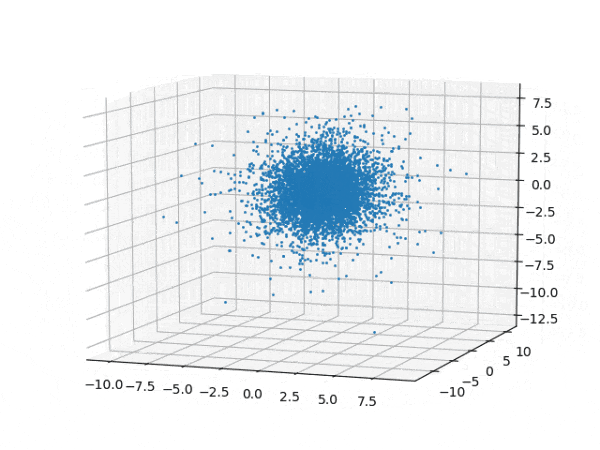
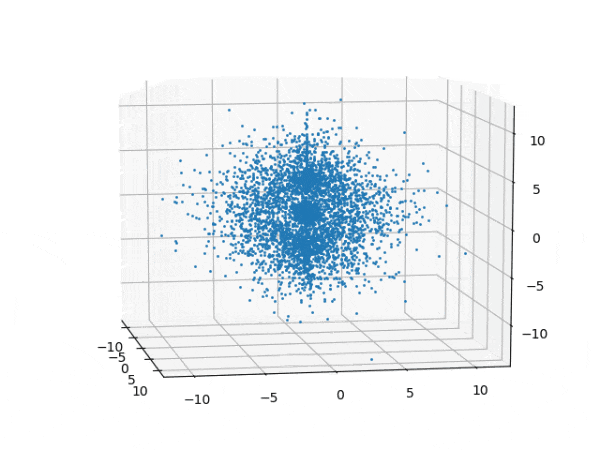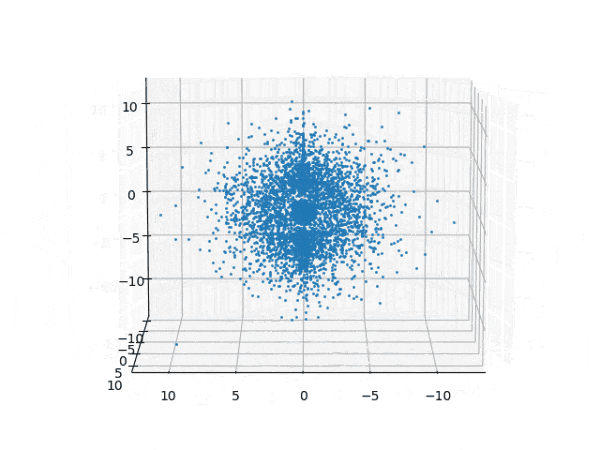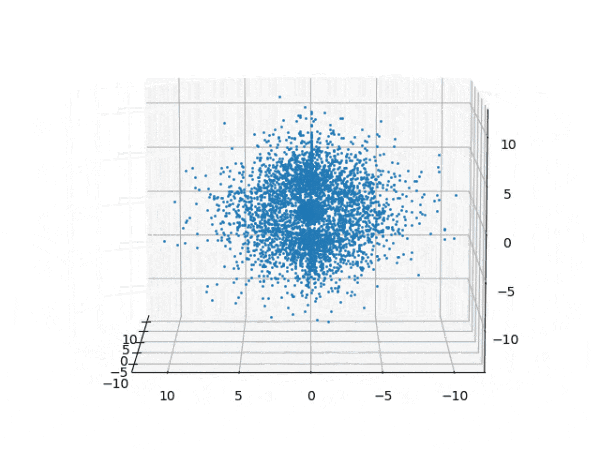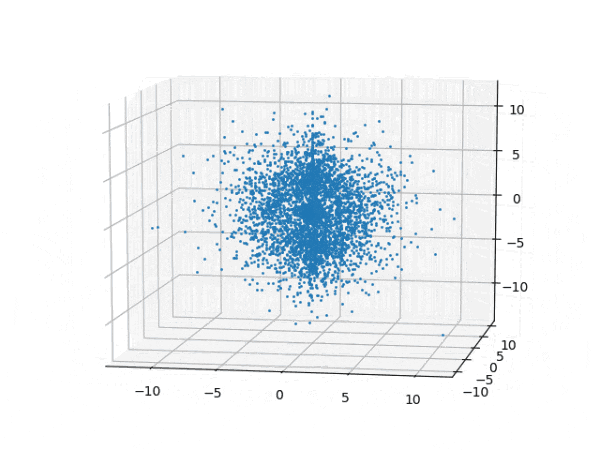
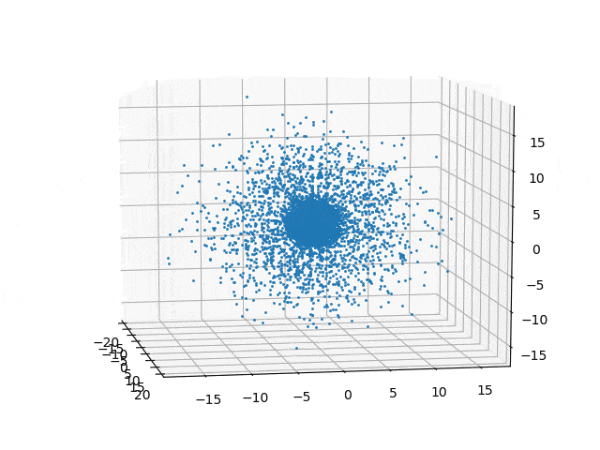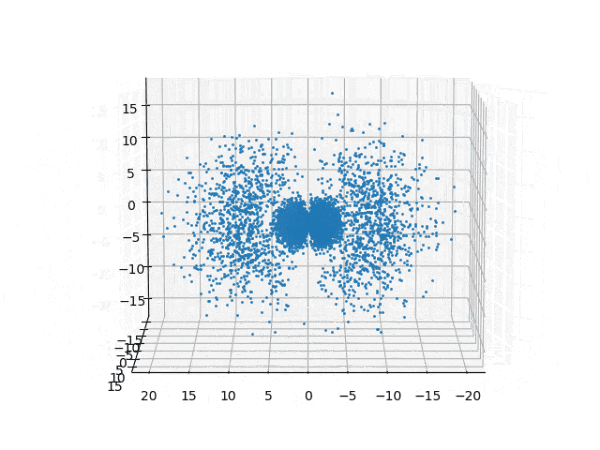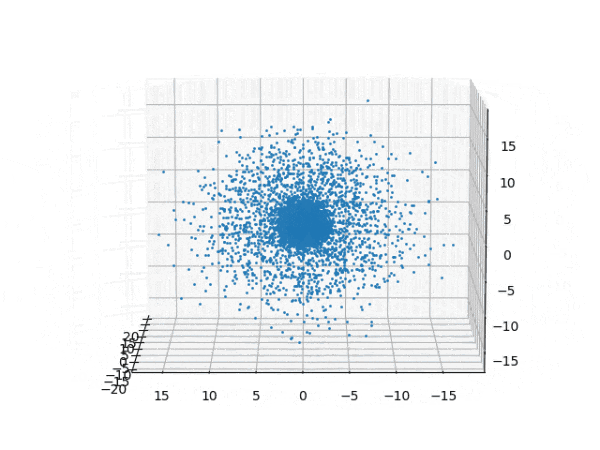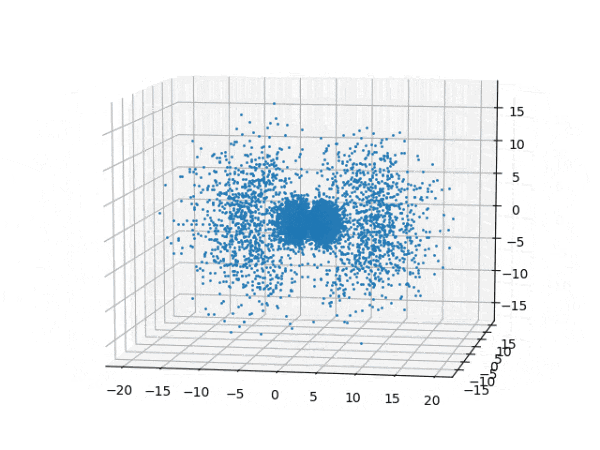
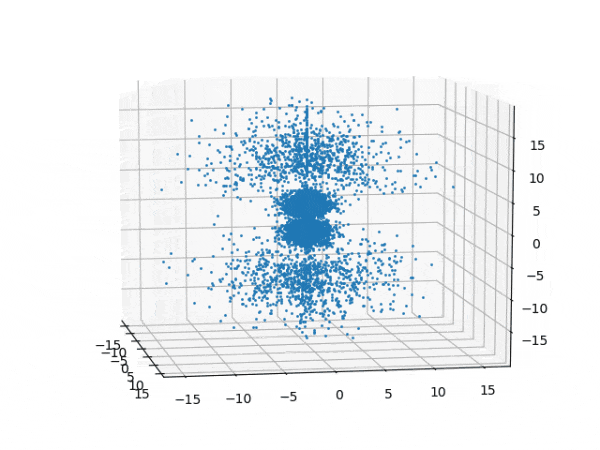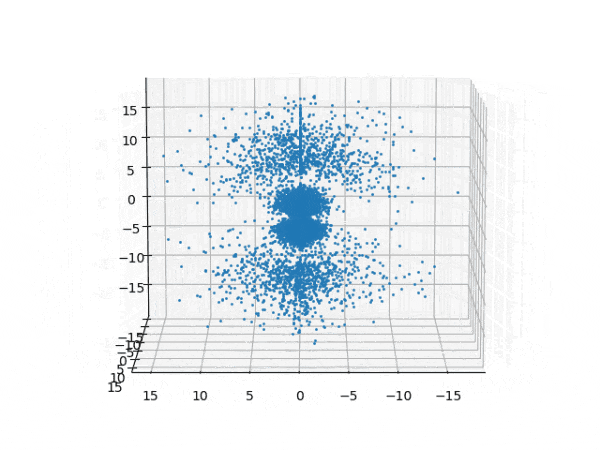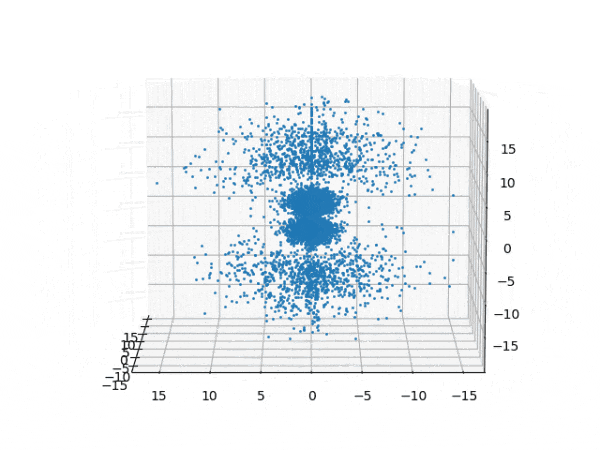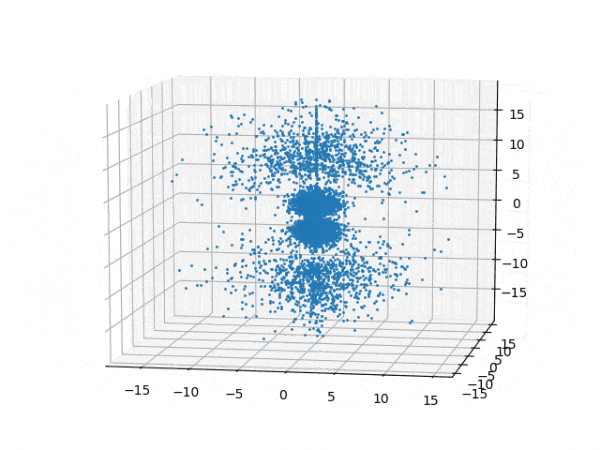
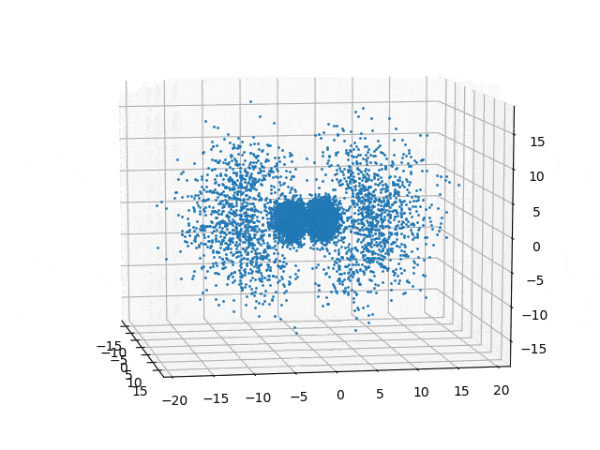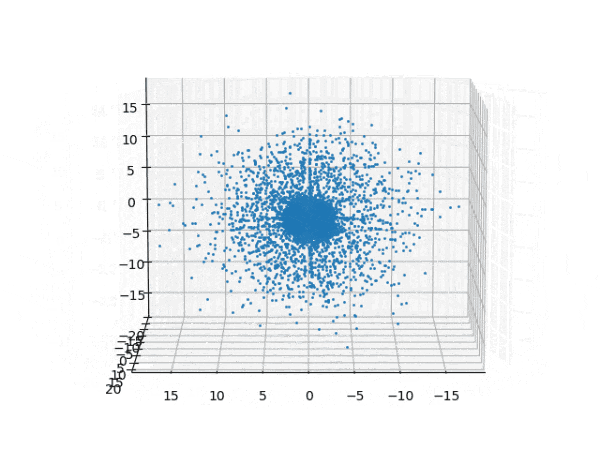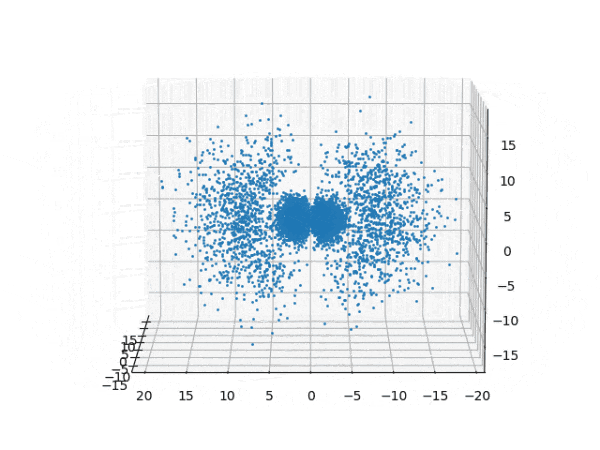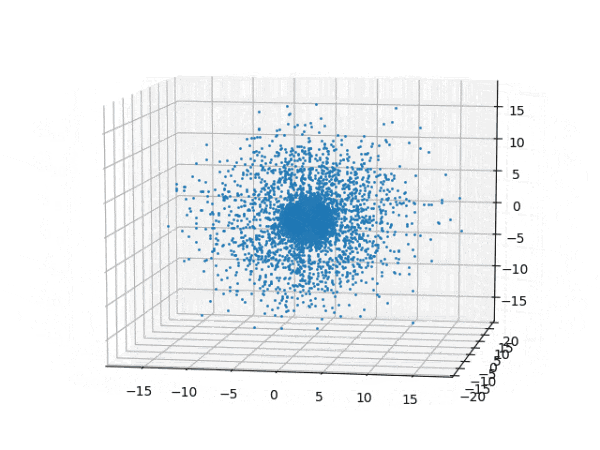
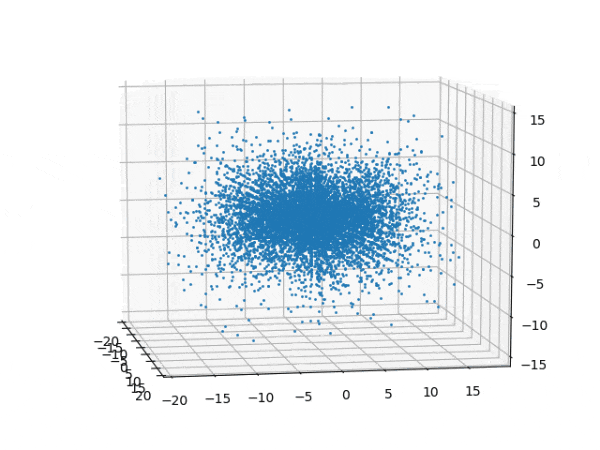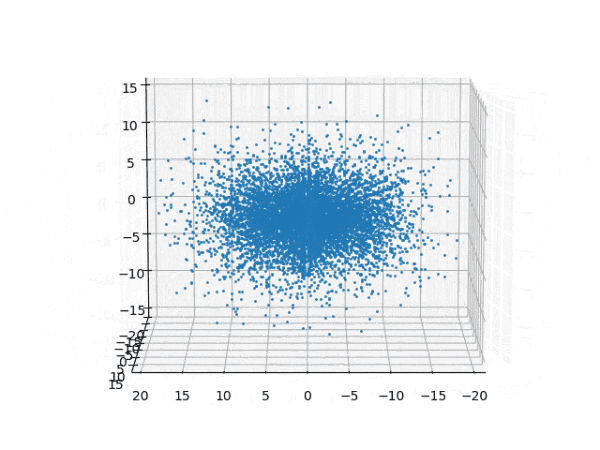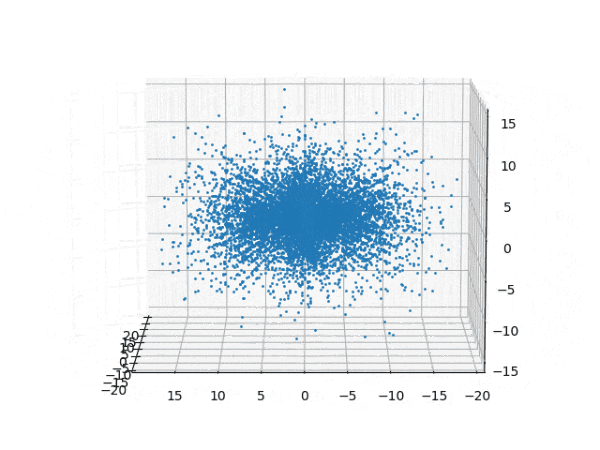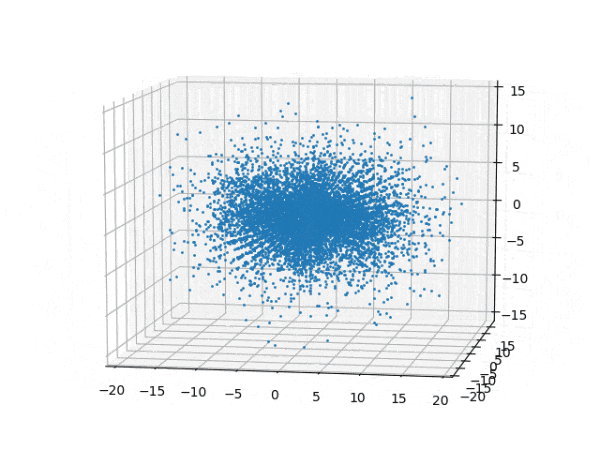
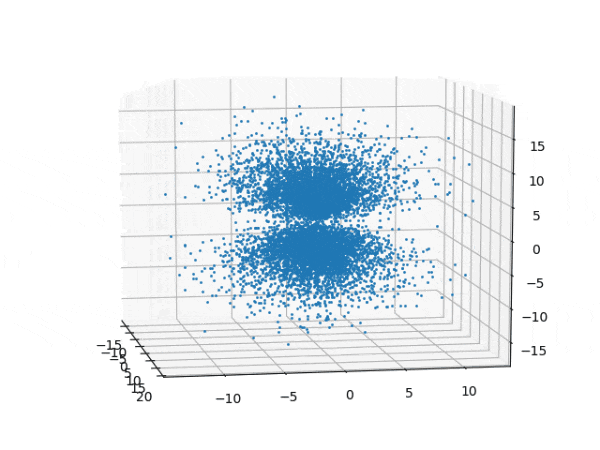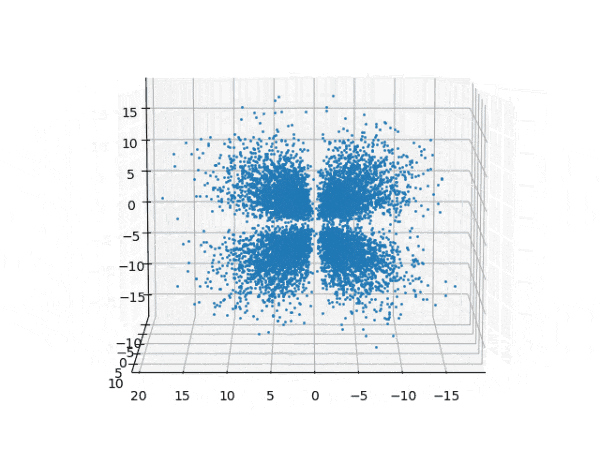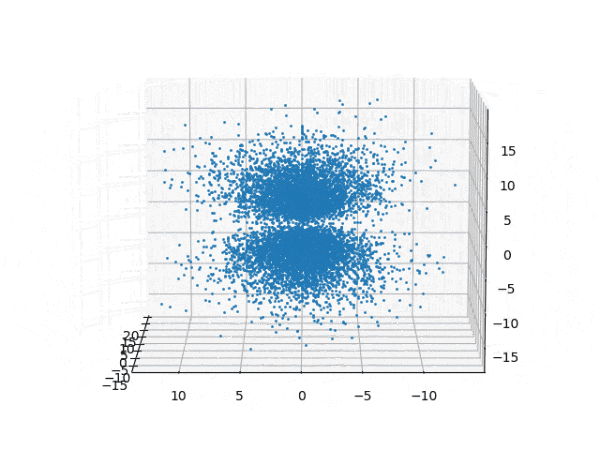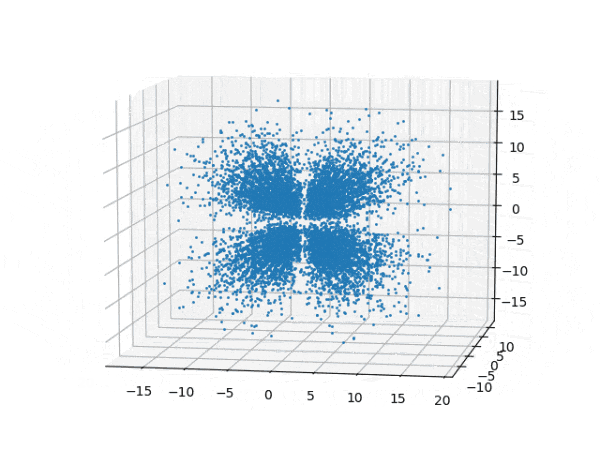
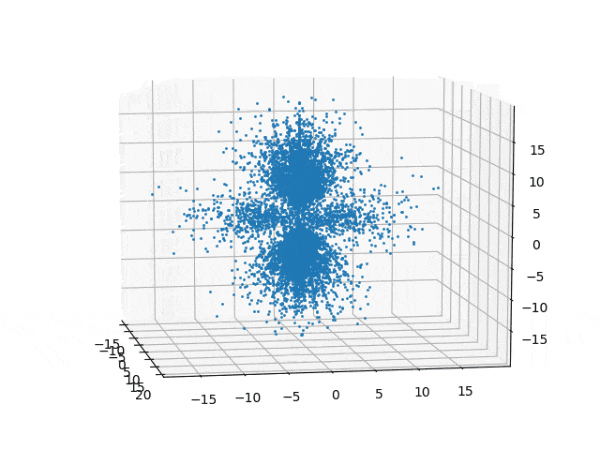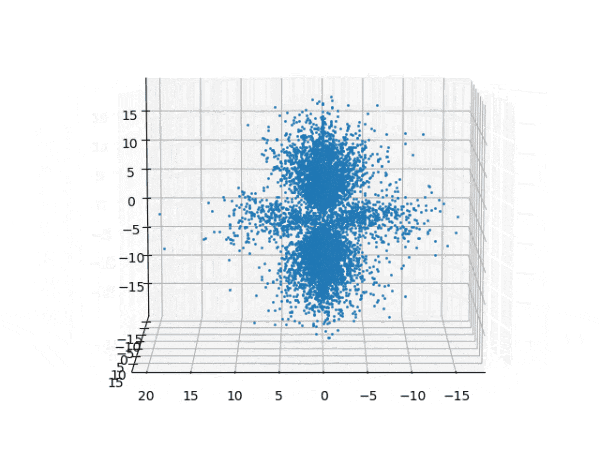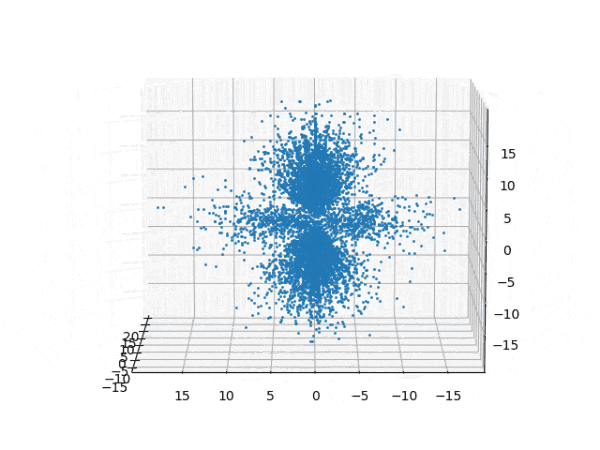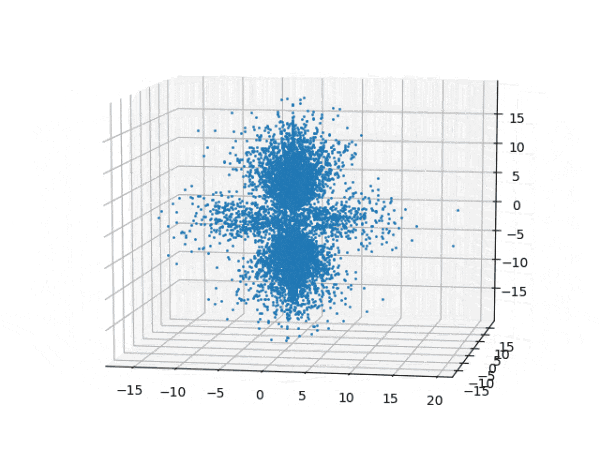
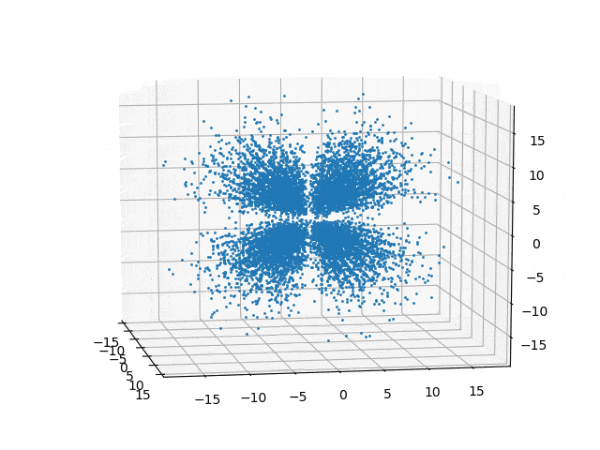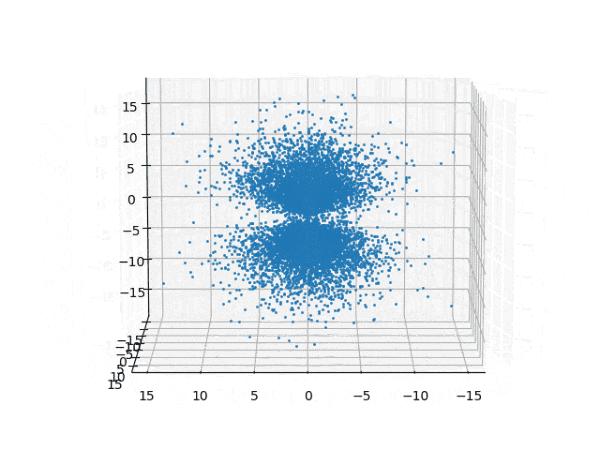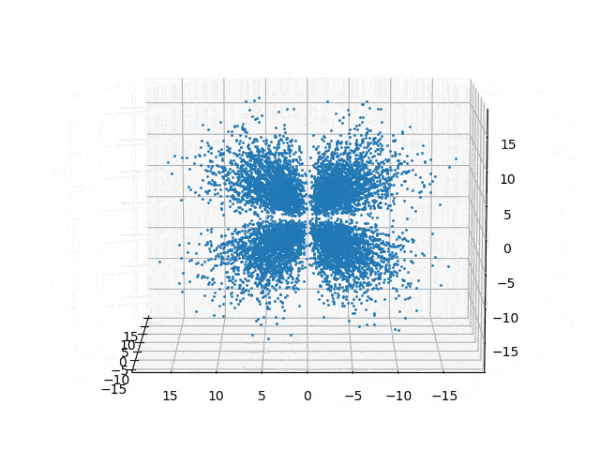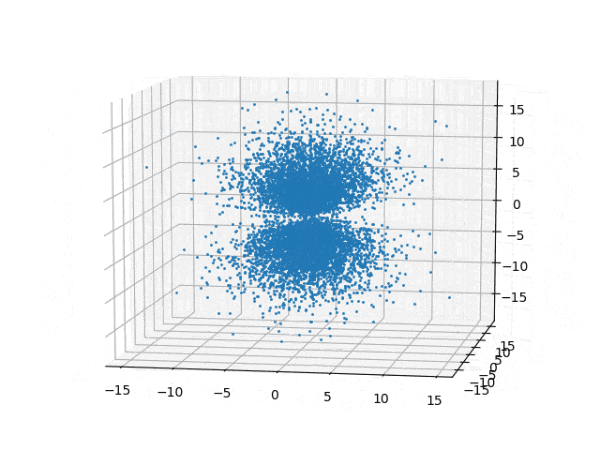
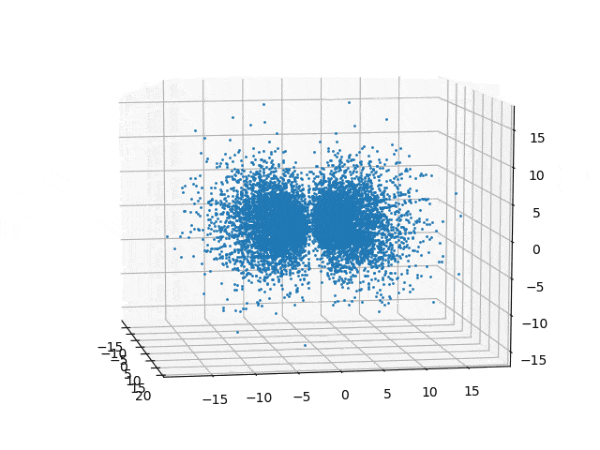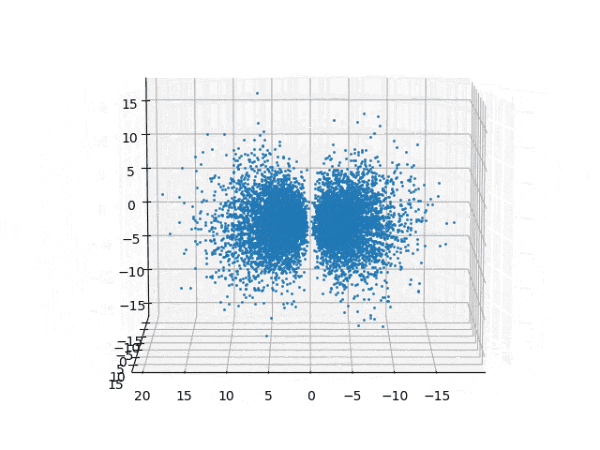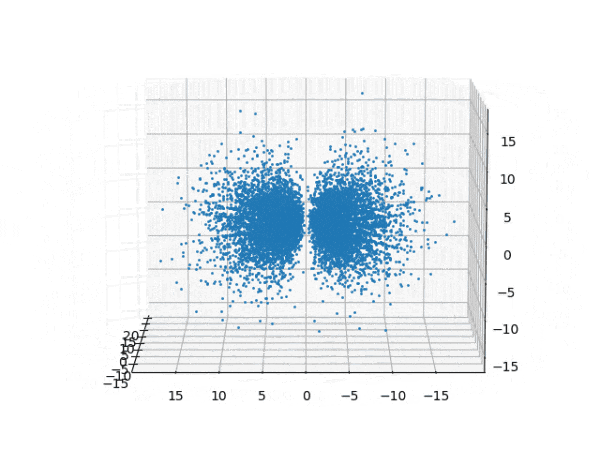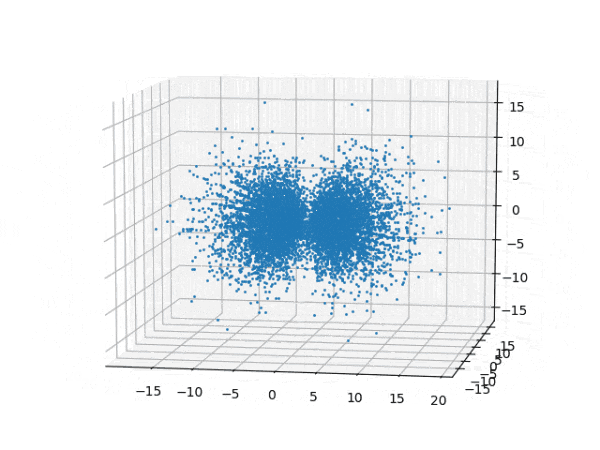
水素原子のシュレディンガー方程式解の波動関数から電子雲の可視化

を元に、水素原子のシュレディンガー方程式の解析解から、

ソースコード

import numpy as np
import os
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D


# 動径関数 R_nl　(A=a0=1, 規格化因子は省略, nは主量子数, lは軌道角運動量量子数) 
# https://ja.wikipedia.org/wiki/%E6%B0%B4%E7%B4%A0%E5%8E%9F%E5%AD%90%E3%81%AB%E3%81%8A%E3%81%91%E3%82%8B%E3%82%B7%E3%83%A5%E3%83%AC%E3%83%BC%E3%83%87%E3%82%A3%E3%83%B3%E3%82%AC%E3%83%BC%E6%96%B9%E7%A8%8B%E5%BC%8F%E3%81%AE%E8%A7%A3

def R_10(r):
    return np.exp(-r)

def R_20(r):
    return (2 - r) * np.exp(-r/2)

def R_21(r):
    return r * np.exp(-r/2)

def R_30(r):
    return (27 - 18*r + r**2) * np.exp(-r/3)

def R_31(r):
    return (6 - r) * r * np.exp(-r/3)

def R_32(r):
    return r**2 * np.exp(-r/3)

# 動径方向関数 Y_lm　(規格化因子は省略。lは軌道角運動量量子数、mは磁気量子数。)

def Y_00(theta, phi):
    return 1

def Y_11(theta, phi):
    return np.sin(theta) * np.cos(phi)

def Y_10(theta, phi):
    return np.cos(theta)

def Y_1_1(theta, phi):
    return np.sin(theta) * np.sin(phi)

def Y_22(theta, phi):
    return np.sin(theta)**2 * np.cos(2*phi)

def Y_21(theta, phi):
    return np.sin(theta) * np.cos(theta) * np.cos(phi)

def Y_20(theta, phi):
    return (3*np.cos(theta)**2 - 1)

def Y_2_1(theta, phi):
    return np.sin(theta) * np.cos(theta) * np.sin(phi)

def Y_2_2(theta, phi):
    return np.sin(theta)**2 * np.sin(2*phi)

def Y_33(theta, phi):
    return np.sin(theta)**3 * np.cos(3*phi)

def Y_32(theta, phi):
    return np.cos(theta) * np.sin(theta)**2 * np.cos(2*phi)

def Y_31(theta, phi):
    return (5*np.cos(theta)**2 -1) * np.sin(theta) * np.cos(phi)

def Y_30(theta, phi):
    return (5*np.cos(theta)**3 - 3*np.cos(theta))

def Y_3_1(theta, phi):
    return (5*np.cos(theta)**2 -1) * np.sin(theta) * np.sin(phi)

def Y_3_2(theta, phi):
    return np.cos(theta) * np.sin(theta)**2 * np.sin(2*phi)

def Y_3_3(theta, phi):
    return np.sin(theta)**3 * np.sin(3*phi)


def generate_hydrogen_orbital_func(nlm, r_range=np.arange(0, 20, 0.1)):
    """
    nlm軌道のR(r)(1次元配列)とY(theta,phi)(2次元配列)の値を計算する。
    Parameter
    ---------
    nlm : 軌道
    ---------
    Returns
    ---------
    R_data : R(r), len(r_range)長の1次元配列
    R_args : R(r)の引数リスト, len(r_range)長の1次元配列
    Y_data : Y(theta, phi), len(theta_range)×len(phi_range)の2次元配列
    Y_args　: Y(theta, phi)の引数リスト,  len(theta_range)×len(phi_range)の2次元配列
    ----------
    """

    if nlm == '100':
        R = R_10
        Y = Y_00
    elif nlm == '200':
        R = R_20
        Y = Y_00
    elif nlm == '211':
        R = R_21
        Y = Y_11
    elif nlm == '210':
        R = R_21
        Y = Y_10
    elif nlm == '21-1':
        R = R_21
        Y = Y_1_1
    elif nlm == '300':
        R = R_30
        Y = Y_00
    elif nlm == '311':
        R = R_31
        Y = Y_11
    elif nlm == '310':
        R = R_31
        Y = Y_10
    elif nlm == '31-1':
        R = R_31
        Y = Y_1_1
    elif nlm == '322':
        R = R_32
        Y = Y_22
    elif nlm == '321':
        R = R_32
        Y = Y_21
    elif nlm == '320':
        R = R_32
        Y = Y_20
    elif nlm == '32-1':
        R = R_32
        Y = Y_2_1
    elif nlm == '32-2':
        R = R_32
        Y = Y_2_2
    else:
        raise ValueError('!!!!')

    # R_nl(r)のデータ生成
    R_data = np.array([R(r) for r in r_range])
    R_args = np.array([r for r in r_range])
    # Y_lm(θ, φ)のデータ生成
    Y_data = np.array([[Y(theta, phi) for theta in np.arange(0, np.pi, 0.1)] for phi in np.arange(0, 2*np.pi, 0.1)])
    Y_args = np.array([[(phi, theta) for theta in np.arange(0, np.pi, 0.1)] for phi in np.arange(0, 2*np.pi, 0.1)])

    return R_data, R_args, Y_data, Y_args


def sample_from_accum_Y(accum_Y):
    """
    Y(θ, φ)^2の累積分布関数accum_Yから1点サンプリングしインデックス(i, j)を返す。
    """

    row_num = accum_Y.shape[0]
    col_num = accum_Y.shape[1]

    # 規格化
    normed_accum = accum_Y / accum_Y[row_num-1, col_num-1]
    rand = np.random.rand()
    for i in range(row_num):
        for j in range(col_num):
            if rand < normed_accum[i, j]:
                return (i, j)


def sample_from_accum_R(accum_R):
    """
    R(r)^2の累積分布関数accum_Rから1点サンプリングしインデックスiを返す。
    """

    # 規格化
    normed_accum = accum_R / accum_R[-1]
    return len(*np.where(normed_accum < np.random.rand()))


OUT_DIR = 'ElectronCloud'
if not os.path.exists(OUT_DIR):
    os.makedirs(OUT_DIR)

# 計算する軌道(nml)リスト
ORBITS = ['100', '200', '211', '210', '21-1', '300', '311', '310', '31-1', '322', '321', '320', '32-1', '32-2']

# 各軌道に対して電子雲を計算する。
for orbit in ORBITS:
    # 軌道orbitのR(r)とY(θ, φ)のデータを生成
    R_data, R_args, Y_data, Y_args = generate_hydrogen_orbital_func(nlm=orbit)
    R_data **= 2
    Y_data **= 2
    #　R^2とY^2の累積分布関数を求める。
    accum_R = np.array([R_data[:i+1].sum() for i in range(len(R_data))])
    accum_Y = np.array([Y_data.flatten()[:i+1].sum() for i in range(len(Y_data.flatten()))]).reshape(Y_data.shape[0], Y_data.shape[1])

    if not os.path.exists(OUT_DIR + '/' + orbit):
        os.makedirs(OUT_DIR + '/' + orbit)

    x = []
    y = []
    z = []
    # 確率分布に従って9000点生成する。
    for _ in range(9000):
        # Y(θ, φ)^2の累積分布関数から(θ,φ)を1組サンプリングする。
        ind_phi, ind_theta = sample_from_accum_Y(accum_Y)
        phi, theta = Y_args[ind_phi, ind_theta]
        # R(r)^2の累積分布関数から1点rをサンプリングする。
        r_ind = sample_from_accum_R(accum_R)
        r = R_args[r_ind]
        x.append(r*np.sin(theta) * np.cos(phi))
        y.append(r*np.sin(theta) * np.sin(phi))
        z.append(r*np.cos(theta))

    fig = plt.figure()
    ax = Axes3D(fig)
    ax.plot(x, y, z, "o", ms=1.5, mew=0.5)

    # 360度回転。10度回転毎に画像を保存
    for i in range(0, 360, 10):
        ax.view_init(elev=10., azim=i)
        plt.savefig(OUT_DIR + '/' + orbit + "/{}.png".format(i))

可視化

nlm = 100

nlm = 200

nlm = 211

nlm = 210

nlm = 21-1

nlm = 300

nlm = 311

nlm = 310

nlm = 31-1

nlm = 322

nlm = 321

nlm = 320

nlm = 32-1

nlm = 32-2