スピンのモンテカルロシミュレーション

ジャロシンスキー守谷相互作用を取り入れ、スピンの向きを多方向許容した場合の2次元スピンのモンテカルロシミュレーションを試みる。

ジャロシンスキー守谷相互作用とは

スピン間に外積の形で働いてくる相互作用。
外積は直交するとき絶対値が最大となるのでスピン同士を直交に向ける働きをする。
スピン間の内積の形で働き並行に向けようとする交換相互作用、磁場$H$の方向に向けようとするゼーマンエネルギーも合わせて、スピン間のエネルギーは

$H_{i,j}=-J\vec{s_i}\cdot\vec{s_j}-\vec{D}\cdot(\vec{s_i}\times\vec{s_j})-\vec{H}\cdot(\vec{s_i}+\vec{s_j})$

第一項がスピン同士を並行に向けようとする交換相互作用、第二項がスピン同士を垂直に向けようとするジャロシンスキー守谷相互作用であり、これらの競合でスピン同士が傾いた状態になる。

今回は2次元のみ考えて($s_z=0$)、$\vec{D}=[0, 0, D]$、$\vec{H}=[0, H, 0]$とする。

$H_{i,j}(\theta)=-J|\vec{s_i}||\vec{s_j}|cos\theta-D|\vec{s_i}||\vec{s_j}|sin\theta-H(s_{iy}+s_{jy})$...①

アルゴリズム

1. スピンをランダムに1個選び、現在のスピンの向き$\theta$からz軸周りに$\Delta \theta(=π/N)$回転した状態を次の向き候補とする。
2. 隣接4個スピンとのエネルギーの和$\sum_j H_{i,j}(\theta)>\sum_j H_{i,j}(\theta+\Delta\theta)$ならば$\Delta \theta$回転した状態を次の状態とする。また、$\sum_j H_{i,j}(\theta)<\sum_j H_{i,j}(\theta+\Delta\theta)$の場合も$\exp(\sum_j H_{i,j}(\theta+\Delta\theta)-\sum_j H_{i,j}(\theta))$の確率で$\Delta \theta$回転した状態を次の状態とする。(MCMCやメトロポリス法のような感じ)
3. ステップ1～2をUPDATE_NUM回行う。
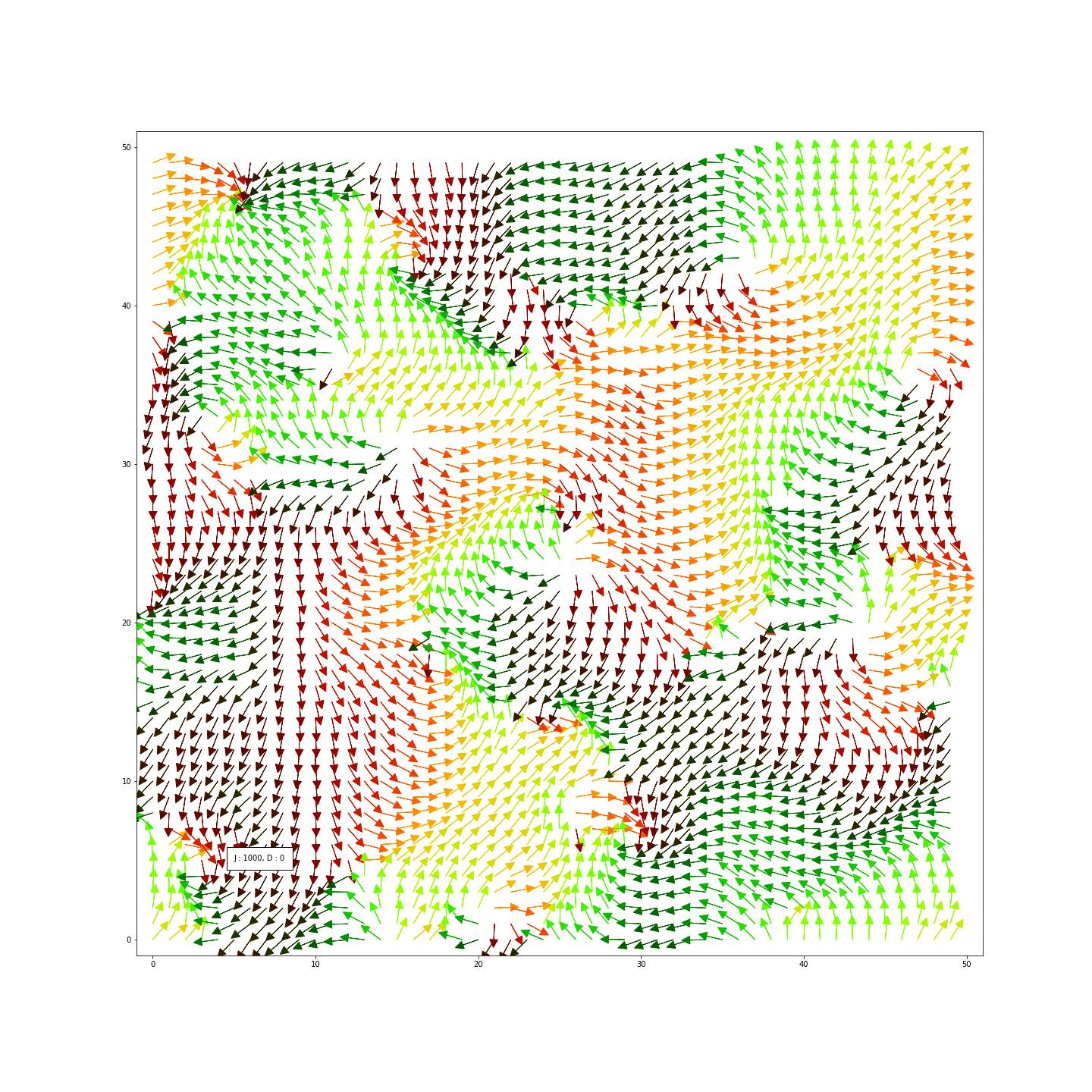
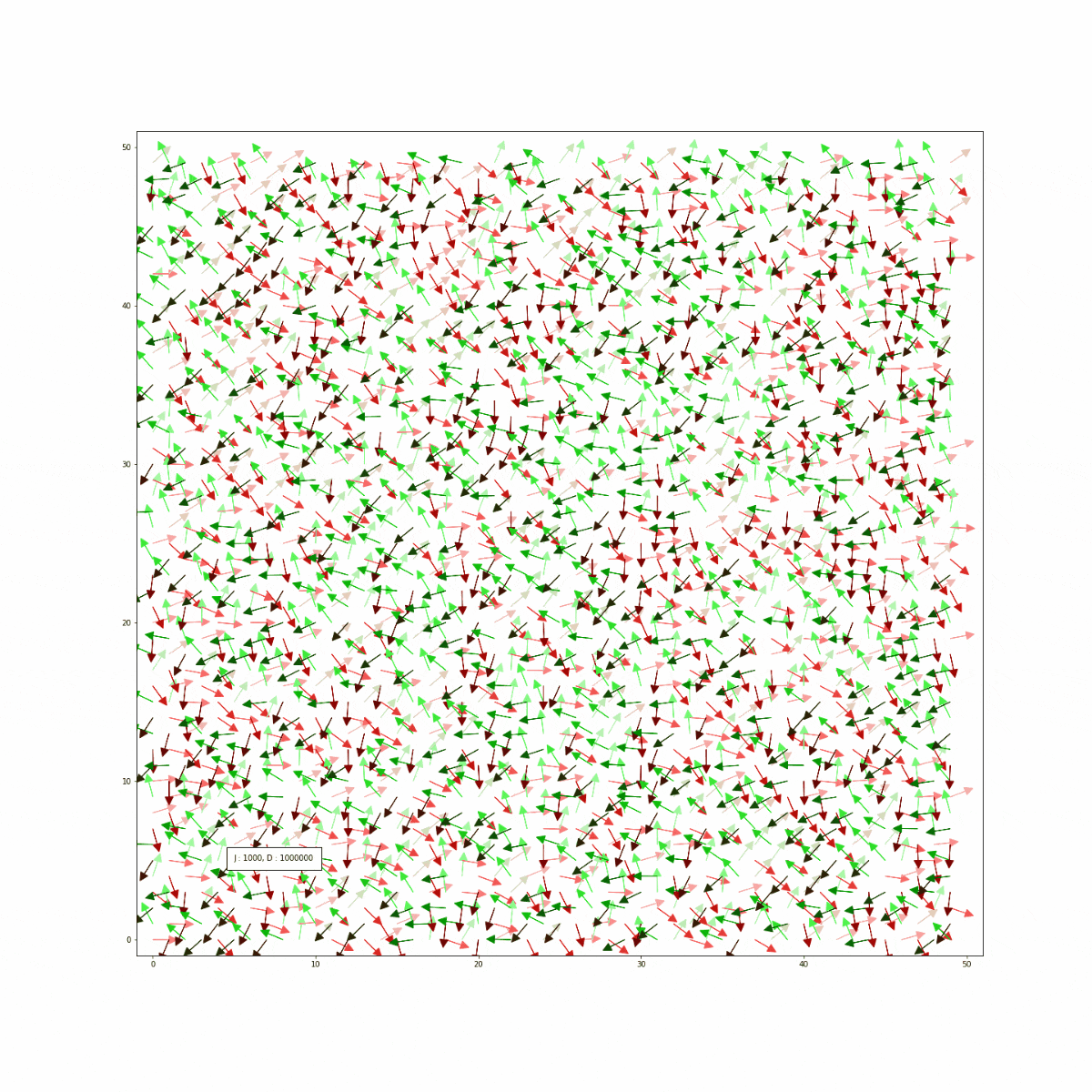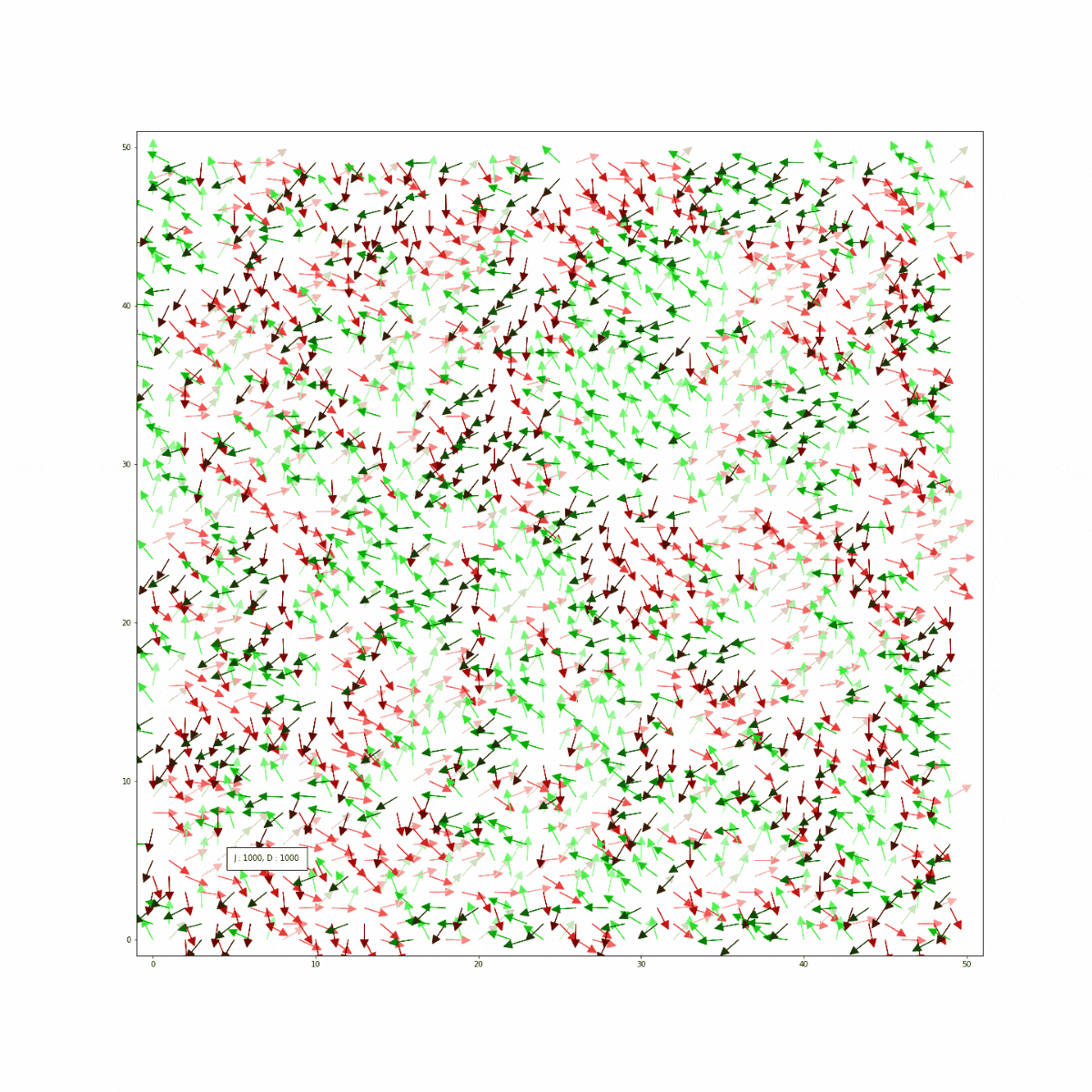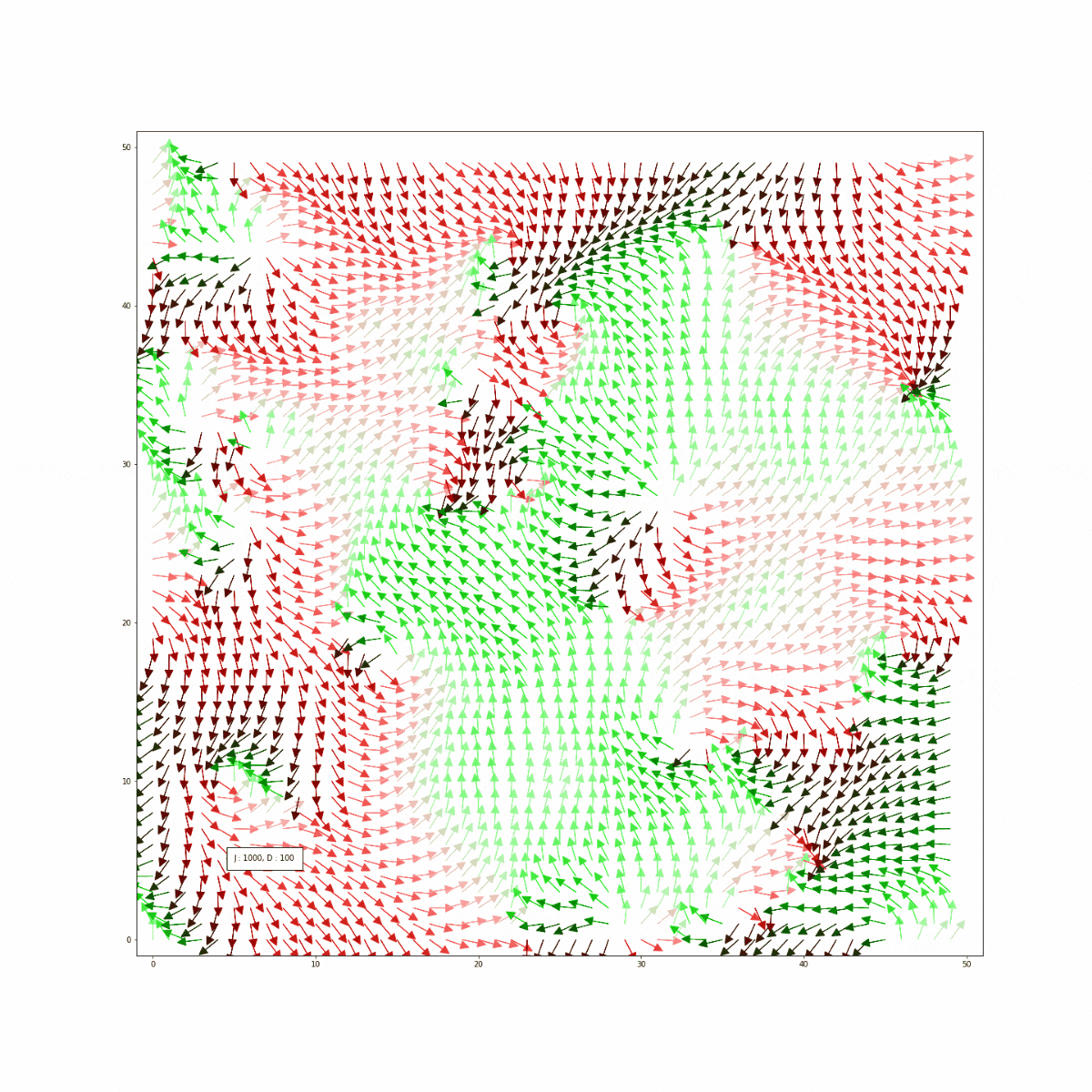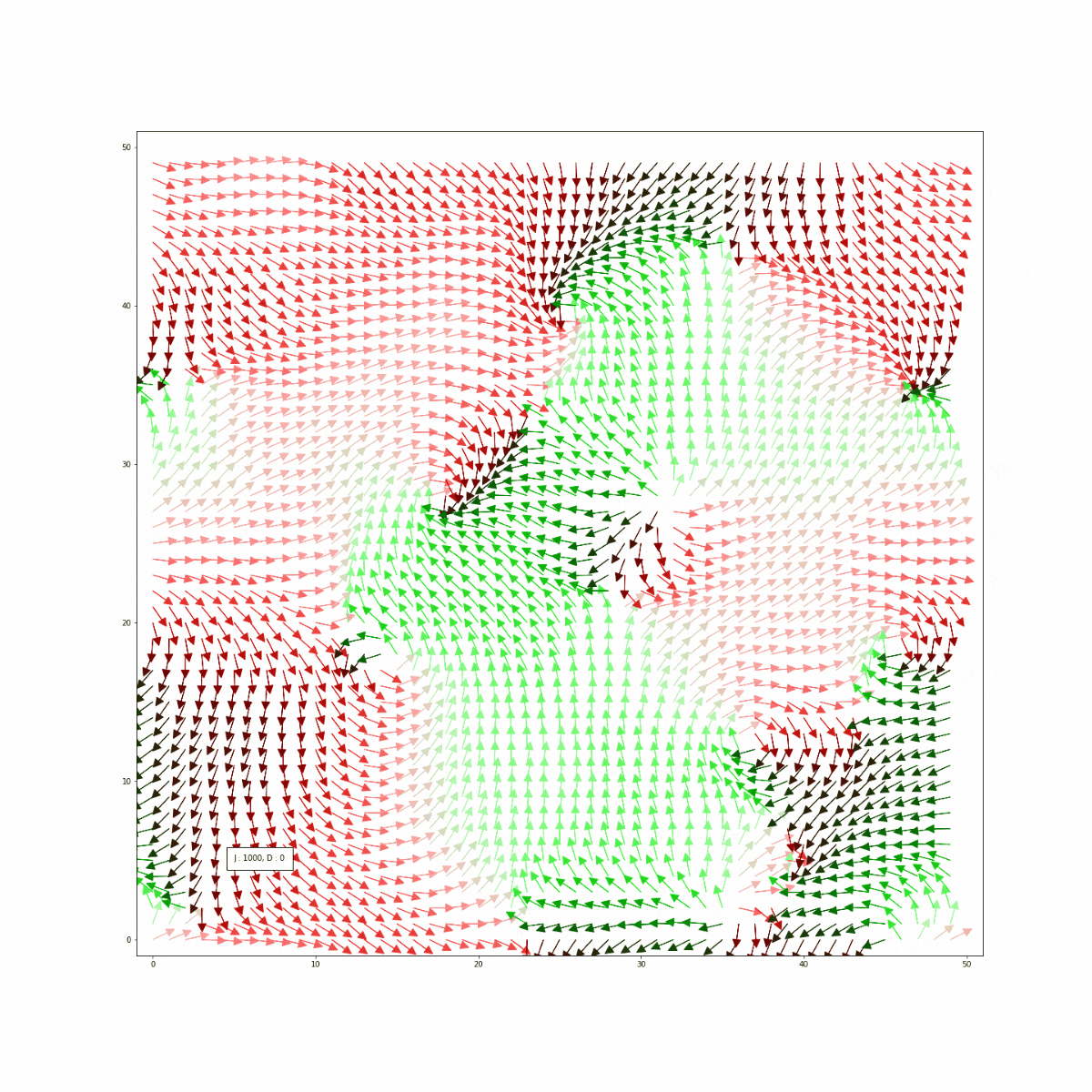
4. 交換相互作用$J$は固定し(1000)、$D$を$D>>J$から0へ減少させながらステップ1～3を繰り返す。

ソース

import numpy as np
import matplotlib.pyplot as plt
from numpy.linalg import norm

N_COL = 50
N_ROW = 50

D_THETA = np.pi / 20  # 40方向程度スピンの向きを許容

J = 1000  # 交換相互作用
D = 1  # ジャロシンスキー守谷相互作用
#H = np.array([0, 800, 0])  # 磁場
H = np.array([0, 0, 0])  # 磁場

UPDATE_NUM = 200000  # 1サイクルあたりのスピン更新回数

def spin_hamiltonian(spin1, spin2, j, d, h=np.zeros(3)):
    """
    式①
    """
    return -j*np.dot(spin1, spin2) - d*norm(np.cross(spin1, spin2)) - np.dot(h, spin1)

def rotate_vec3d(vec3d, theta):
    """
    3次元ベクトルvec3dをz軸周りにtheta回転
    """
    rot_mat = np.matrix((
        (np.cos(theta), np.sin(theta), 0.0),
        (-np.sin(theta), np.cos(theta), 0.0),
        (0.0, 0.0, 1.0)
    ))
    return np.dot(rot_mat, vec3d)

# スピンマップ初期化
# ランダム方向のスピンを生成
thetas = np.random.rand(N_COL*N_ROW)*2.0*np.pi
spins = np.array(list(map(lambda theta: (np.cos(theta), np.sin(theta), 0.0), thetas)))
#spins = np.array(list(map(lambda theta: (0.0, 1.0, 0.0), thetas)))
print(spins.shape)
spinmap = spins.reshape(N_ROW, N_COL, 3)

# ランダムに選ぶスピンのインデックスリスト
rand_index_x = np.random.randint(0, N_COL, UPDATE_NUM)
rand_index_y = np.random.randint(0, N_ROW, UPDATE_NUM)
rand_rotation_dir = np.random.randint(0, 2, UPDATE_NUM)
print(rand_rotation_dir[:10])


for cnt, d in enumerate(reversed([0, 0, 0, 0, 0, 0, 0, 10, 50, 100, 200, 300, 400, 500, 600, 700, 1000, 1300, 1500, 3000, 5000, 10000, 20000])):
    print(d)
    for i_x, i_y, r_dir in zip(rand_index_x, rand_index_y, rand_rotation_dir):

        cur_energy = 0
        next_energy = 0
        # 現在のスピンをD_THETAだけ回転させ次の状態候補とする
        rotated_spin = rotate_vec3d(spinmap[i_y, i_x], D_THETA*(1 if r_dir == 0 else -1))
        for dx, dy in ((1,0), (0,1), (-1,0), (0, -1)):
            try:
                cur_energy += spin_hamiltonian(spinmap[i_y, i_x], spinmap[i_y+dy, i_x+dx], j=J, d=d, h=H)
                next_energy += spin_hamiltonian(rotated_spin, spinmap[i_y+dy, i_x+dx], j=J, d=d, h=H)
            except Exception as e:
                # 端っこは無視
                pass
        
        # 次の状態のほうがエネルギーが低い場合
        if cur_energy > next_energy:
            spinmap[i_y, i_x] = rotated_spin / norm(rotated_spin)
        elif np.exp(cur_energy - next_energy) > np.random.rand():
            spinmap[i_y, i_x] = rotated_spin / norm(rotated_spin)
        
    # スピンの描画
    plt.clf()
    plt.figure(figsize=(20, 20))
    ax = plt.axes()
    plt.xlim(-1, N_COL+1)
    plt.ylim(-1, N_ROW+1)
    plt.text(5, 5, 'J : {}, D : {}'.format(J, d) , bbox={'facecolor': 'white', 'pad': 10})
    for i in range(N_ROW):
        for j in range(N_COL):
            red = 0.5*(1+spinmap[i,j][0])
            green = 0.5*(1+spinmap[i,j][1])
            blue = red*green
            ax.arrow(i, j, spinmap[i,j][0], spinmap[i,j][1], head_width=0.5, head_length=0.5, color=(red, green, blue, 1))
    plt.savefig('spins_J-{}_D-{}_{}'.format(J, d, cnt))

結果

See the Pen WJRgrY by popondelion (@popondelion) on CodePen.