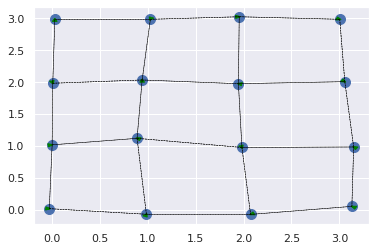
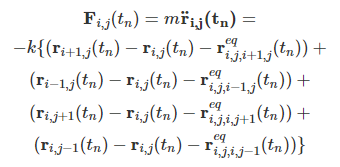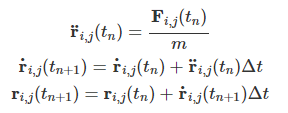こちらの文献を参考に、下図の状況のようなバネにつながれた物体のダイナミクスのNNによる学習・予測を試してみます。
具体的には時刻$t_n$までの各物体の位置$\mathbf{r(t_n)}$、速度$\mathbf{\dot{\mathbf{r}}(t_n)}$、加速度$\mathbf{\ddot{\mathbf{r}}(t_n)}$を入力として、一期先時刻$t_{n+1}$での加速度変化($\mathbf{\ddot{\mathbf{r}}(t_{n+1})}$-$\mathbf{\ddot{\mathbf{r}}(t_n)}$)を予測します。
※文献の詳細は読めていないので、思想的なところだけ参考に試していきます。
大まかな流れ
- 運動方程式から数値計算を行いていくつかの初期条件で教師データを生成
- 1で作成した教師データを用いてNNモデルを学習
- 適当な状態からその先の状態をNNモデルから逐次的に予測し、それらしい運動になるか確認する。
1. 教師データの生成
簡易のため、適当な初期状態を生成後、運動方程式からEuler法により逐次計算を行います。
- 位置$\mathbf{r}_{i, j}$の物体の運動方程式
上下左右4方向からの力の和で、$m$は質量、$\mathbf{r}^{eq}_{i,j,i\prime,j\prime}$は$(i,j)$の物体から$(i\prime, j\prime)$の物体を向いた平衡位置のベクトル、$k$はばね定数です。端っこの連結がない部分は除外します。
上記式から、以下Euler法で一期先の状態を計算します
- 物体定義と初期化
@dataclass
class Obj:
idx: int
pos: np.array
vel: np.array
accel: np.array
force: np.array
connected_objs: List = None
mass: float = 1.0
energy: float = 0.0
def init_objs_2d():
objs = {}
# 物体作成
for i in range(4):
for j in range(4):
objs[(i,j)] = Obj(
idx=i*4+j,
pos=np.array([i, j])+0.05*np.random.randn(2),
vel=0.01*np.random.randn(2),
accel=np.zeros(2),
force=np.zeros(2),
)
# バネ連結情報付与
for i in range(4):
for j in range(4):
connected_objs = []
if i-1 >= 0:
connected_objs.append(objs[(i-1,j)])
if i+1 <= 3:
connected_objs.append(objs[(i+1,j)])
if j-1 >= 0:
connected_objs.append(objs[(i,j-1)])
if j+1 <= 3:
connected_objs.append(objs[(i,j+1)])
objs[(i,j)].connected_objs = connected_objs
return objs
- 各種状態更新関数
def force(pos1: np.array, pos2: np.array):
"""pos2の物体からpos1の物体に働くフックの法則による力"""
dist = np.sqrt(((pos1-pos2)**2).sum())
r_normed = (pos2-pos1)/dist
equilibrium_vec = EQUILIBRIUM_LENGTH*r_normed
f = -K*(equilibrium_vec-(pos2-pos1))
return f
def _update_force_on_obj(obj: Obj):
"""物体に働く力の更新"""
forces = [force(obj.pos, obj2.pos) for obj2 in obj.connected_objs]
obj.force = sum(forces)
def _update_accel(obj: Obj):
"""物体の加速度更新"""
obj.accel = obj.force / obj.mass
def _update_velocity(obj: Obj):
"""物体の速度更新"""
obj.vel = obj.vel + DT*obj.accel
def _update_pos(obj: Obj):
"""物体の位置更新"""
obj.pos = obj.pos + DT*obj.vel
def update_states(objs: List[Obj]):
"""全物体の状態更新"""
[_update_force_on_obj(obj) for obj in objs.values()]
[_update_accel(obj) for obj in objs.values()]
[_update_velocity(obj) for obj in objs.values()]
[_update_pos(obj) for obj in objs.values()]
[_calc_energy(obj) for obj in objs.values()]
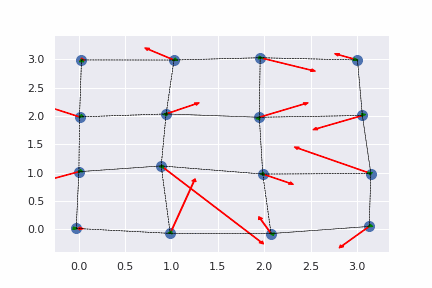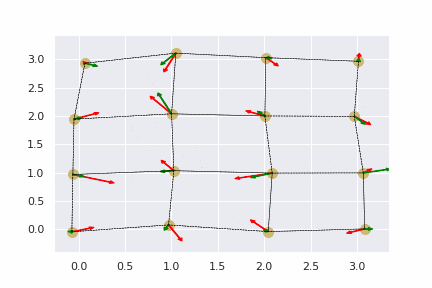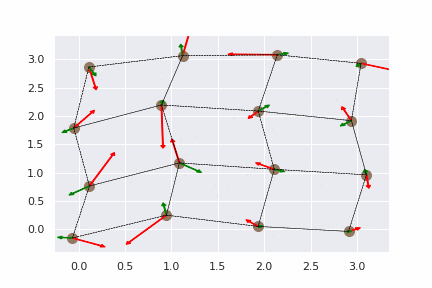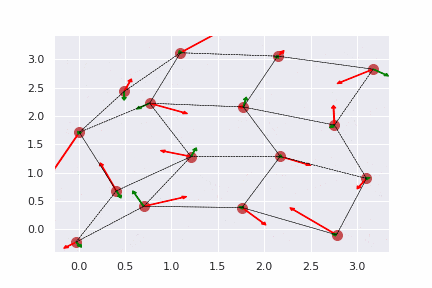
- 計算結果の可視化
赤い矢印が物体に働いているフックの法則による力のベクトルで、緑の矢印が物体の速度ベクトルです。
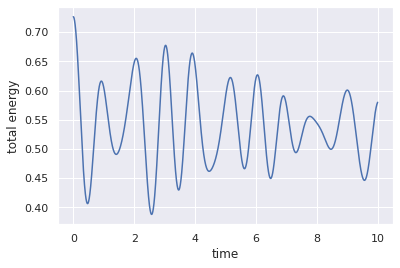
全力学的エネルギーの時間変化も確認してみます。
保存されていないみたいですが、気にせず進みます。
2. ニューラルネットワークモデルの学習
1で生成したデータから、各物体の時刻$t_n$までの各物体の状態を入力、各物体の一期先$t_{n+1}$の加速度変化を出力としたグラフニューラルネットワークを学習します。
モデル構造
モデル全体像イメージは冒頭で述べた文献記載の下図モデルを大まかに参考にし、GNがグラフニューラルネットワーク(GNN)モジュール、エンコーダー部分の詳細は分からなかったのでエンコーダーは除外、デコーダーは単純に全結合層にしました。
グラフにおいて、物体がノード、物体をつなげてるバネがエッジで、ノード(物体)に特徴量(位置、速度等)が紐づいているイメージです。
- GNNモジュール
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch_geometric.nn import GCNConv
class GNNModule(torch.nn.Module):
def __init__(self, n_features, out_dim, intermediate_dim=24):
super(GNNModule, self).__init__()
self.conv1 = GCNConv(n_features, intermediate_dim)
self.conv2 = GCNConv(intermediate_dim, out_dim)
def forward(self, x, edge_index):
x2 = self.conv1(x, edge_index)
x3 = F.relu(x2)
x4 = F.dropout(x3, training=self.training)
x5 = self.conv2(x4, edge_index)
return x5
(バッチサイズ, ノード数(物体数), n_features)のfeatureと、(2, エッジ数(バネの数))のedge_indexを入力すると、(バッチサイズ、out_dim)のテンソルが出力されます。
- 全体ネットワーク
class SpringDynamicsNet(torch.nn.Module):
def __init__(self, n_features, out_dim, n_gnn_module=4, intermediate_dim=24):
super(SpringDynamicsNet, self).__init__()
self._intermediate_gnn_modules = nn.Sequential(
*[GNNModule(n_features, n_features) for _ in range(n_gnn_module)]
)
self._fc = nn.Linear(n_features, out_dim)
def forward(self, x, edge_index):
for sping_module in self._intermediate_gnn_modules:
residual = x
gnn_out = sping_module(x, edge_index)
x = residual + gnn_out
return self._fc(x)
(バッチサイズ, ノード数(物体数), n_features)のfeatureと、(2, エッジ数(バネの数))のedge_indexを入力すると、(バッチサイズ、out_dim)のテンソルが出力されます。
入出力データ
入力の状態は時刻$t_n$における各物体の位置・加速度、$t_n$から$N$期前までの各物体の速度とし、今回は$N$は3で行い、出力は1期先の加速度変化としました。
具体的に書くと、物体1つに対し、入力は
$[x(t), y(y), v_x(t), v_y(t), v_x(t-1), v_y(t-1), v_x(t-2), v_y(t-2), v_x(t-3), v_y(t-3), a_x(t), a_y(t)]$
出力は
$[a_x(t+1)-a_x(t), a_y(t+1)-a_y(t)]$
といった感じです。
これが物体数(16)あるので、入力が(バッチサイズ、16, 12)、出力が(バッチサイズ、16, 2)のテンソルになります。
モデル入力には上記に加え、下記の物体連結情報のエッジデータも渡します。
エッジデータ作成
連結している物体のインデックスペアリストを作ります。
edge_index = {}
for obj in objs.values():
for obj2 in obj.connected_objs:
edge_index[(obj.idx, obj2.idx)] = 1
edge_index = list(edge_index.keys())
edge_index = torch.tensor(edge_index).T
学習
spring_dynamics_net = SpringDynamicsNet(
n_features=FEATURE_DIM,
out_dim=2,
n_gnn_module=4,
intermediate_dim=24
)
criterion = nn.MSELoss()
optimizer = torch.optim.Adam(spring_dynamics_net.parameters(), lr=0.01, weight_decay=5e-4)
BATCH_SIZE = 32
N_EPOCHS = 20
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
spring_dynamics_net.to(device)
spring_dynamics_net.train()
loss_histroy = []
for epoch in pb(range(N_EPOCHS)):
epoch_loss = 0
for i in range(feats.shape[0]//BATCH_SIZE):
feat_batch = feats[i*BATCH_SIZE:(i+1)*BATCH_SIZE, :, :]
out_batch = outs[i*BATCH_SIZE:(i+1)*BATCH_SIZE, :, :]
optimizer.zero_grad()
preds = spring_dynamics_net(feat_batch, edge_index)
loss = criterion(out_batch, preds)
loss.backward(retain_graph=True)
optimizer.step()
epoch_loss += loss.item()*feat_batch.shape[0]
loss_histroy.append(epoch_loss)
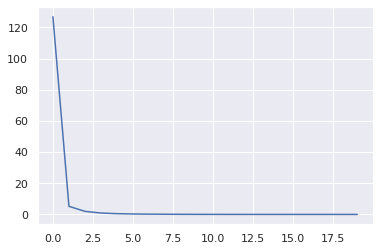
- 損失時系列
学習できてるようです。