多目的最適化
多目的最適化とは, トレードオフの関係にある複数の目的関数を同時に最適化することです.
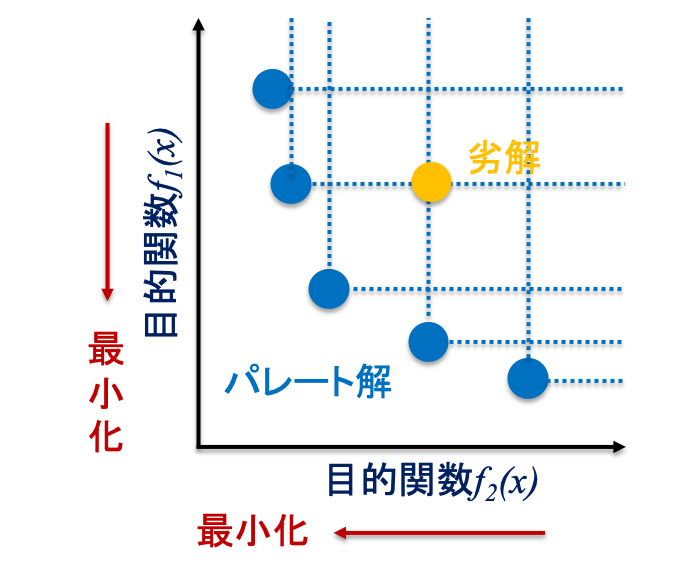
単目的最適化の場合は最適解は一つですが, 多目的最適化の場合は最適解は一つとは限りません. 多目的最適化における最適解はパレート最適解と呼ばれます. パレート最適解に関する図を下に示します.
platypus
platypusは, 多目的最適化用のライブラリの一つであるようです.
具体的には, NSGA-II, NSGA-III, MOEA/D, IBEA, Epsilon-MOEA, SPEA2, GDE3, OMOPSO, SMPSO, Epsilon-NSGA-IIなど数多くの手法が使用可能なようです.
使用するにはpipでインストールしましょう.
pip install platypus-opt
テスト問題
Platypusには, テスト問題も用意されています.
今回は, DTLZ2というテスト問題を使用してみましょう.
from platypus import NSGAII, Problem, Real, nondominated, Integer
import matplotlib.pyplot as plt
from platypus.problems import DTLZ2
def main():
# 問題, アルゴリズムを設定し, 探索実行
problem = DTLZ2(2)
algorithm = NSGAII(problem, population_size=100)
algorithm.run(10000)
# 非劣解をとりだす
nondominated_solutions = nondominated(algorithm.result)
# グラフを描画
plt.scatter([s.objectives[0] for s in nondominated_solutions if s.feasible],
[s.objectives[1] for s in nondominated_solutions if s.feasible])
plt.show()
if __name__ == '__main__':
main()
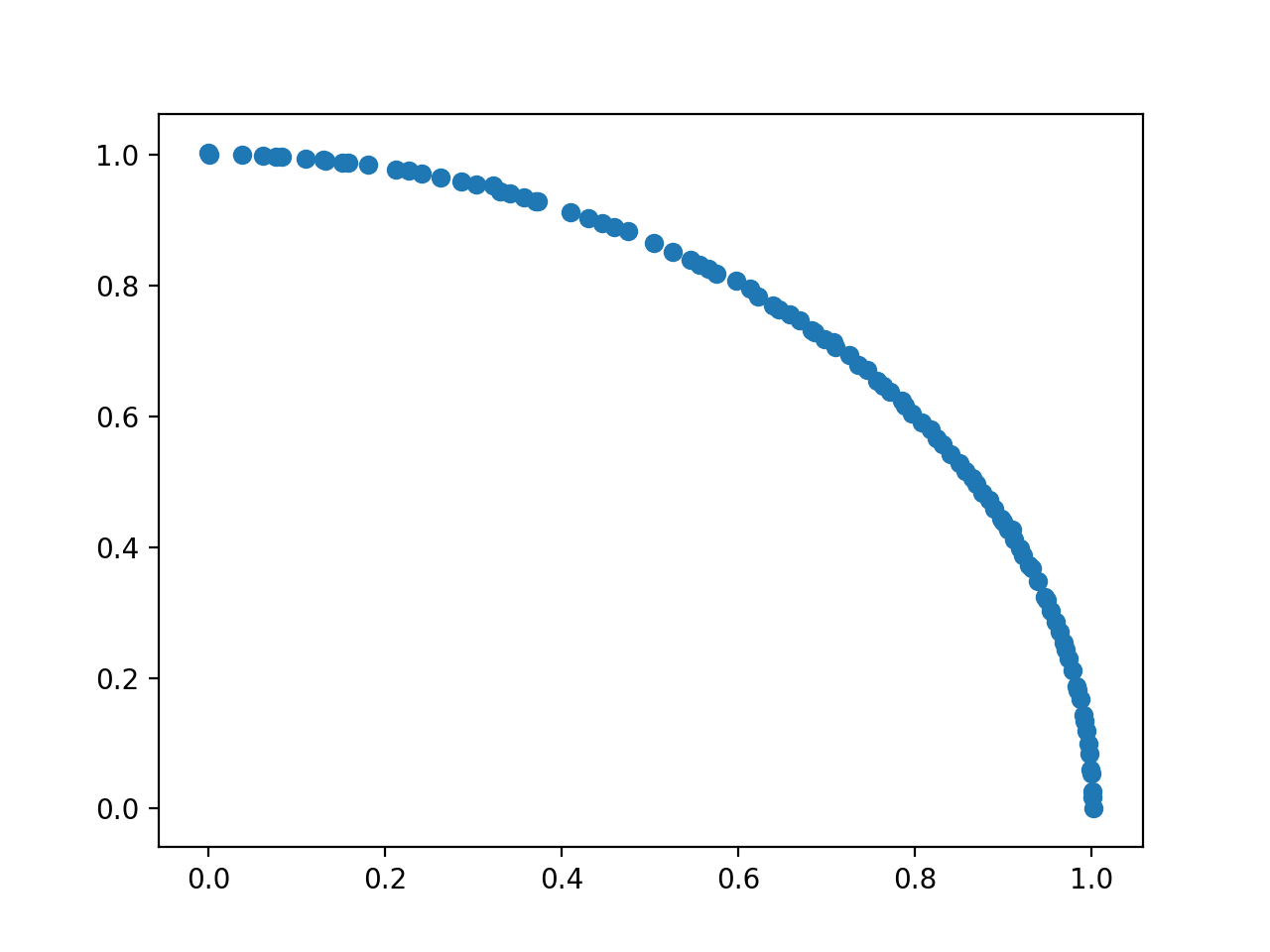
DTLZ2(2)として2目的問題として最適化した結果は以下のようになりました. パレート最適解が獲得されたのが確認できました.
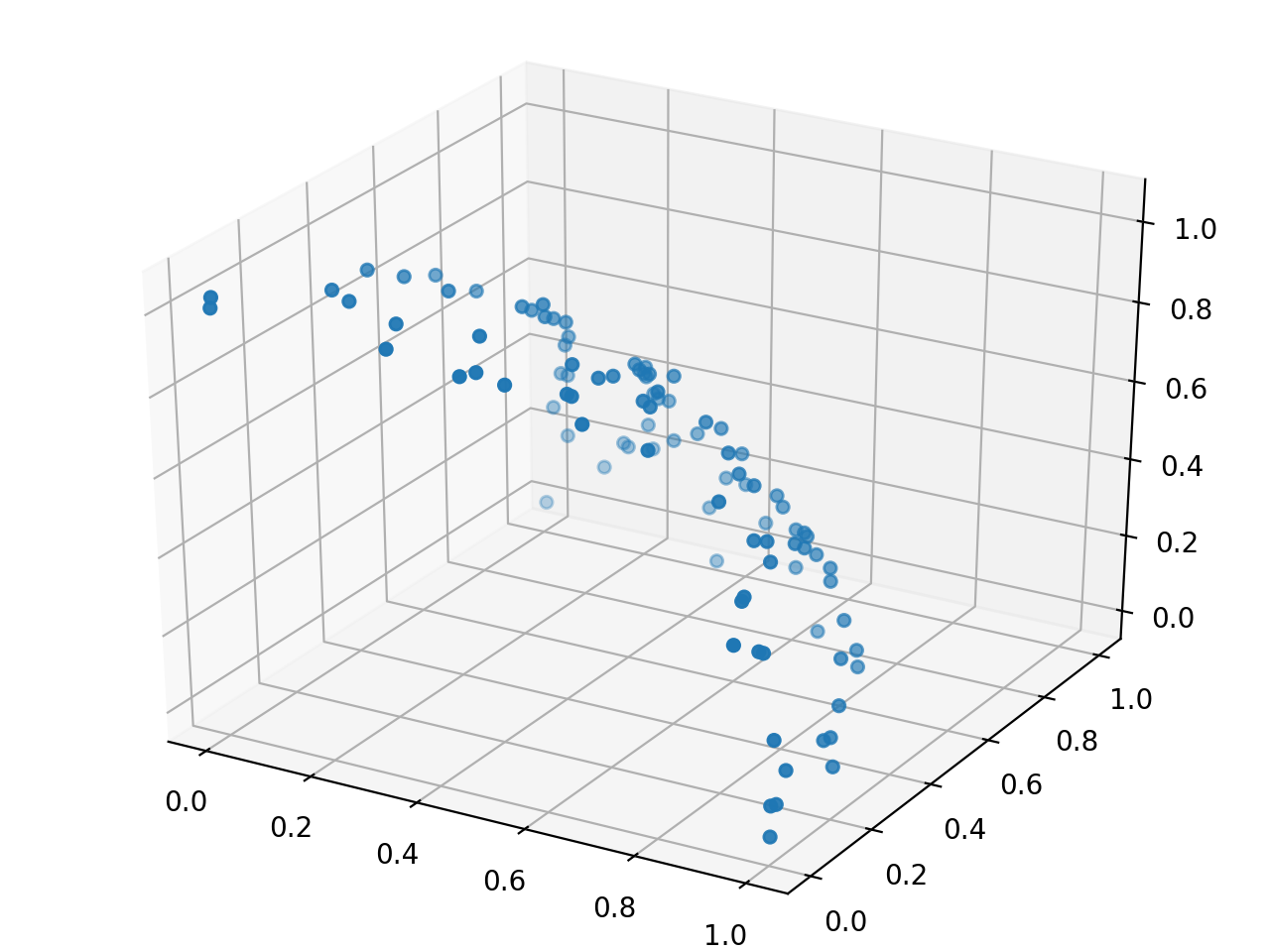
DTLZ2(3)として3目的問題としても最適化してみました.
問題を作って最適化
Platypusでは, 自分で設定した問題を最適化することもできます.
まずは目的関数の設定をしましょう.
今回は2変数2目的最小化問題を最適化していきます. 以下2つを目的関数とします.
f(x)=2x_1^2+x_2^2
g(x)=-x_1^2-2x_2^2
# 目的関数の設定
def objective(vars):
x1 = int(vars[0])
x2 = int(vars[1])
return [2*(x1**2) + x2**2, -x1**2 -2*(x2**2)]
目的関数の設定が終われば, 探索の設定をしていきましょう.
Problem(変数の数, 目的関数の数)で問題の設定ができます.
# 2変数2目的の問題
problem = Problem(2, 2)
problem.directions[:] = Problem.MINIMIZEで最小化問題として設定しています. 最大化問題としたいならProblem.MAXIMIZEで設定できます.
最小化, 最大化を混在させたいなら, 目的変数ごとに設定することもできます.
例えば, problem.directions[:] = [Problem.MINIMIZE, Problem.MAXIMIZE]などとすることができます.
# 最小化or最大化を設定
problem.directions[:] = Problem.MINIMIZE
次に決定変数の設定をしましょう.
今回は$x_1$と$x_2$ともに整数として, 範囲は$0\leq x_1\leq100$と$0\leq x_2\leq50$としています.
今回は決定変数を整数としていますが, 実数で扱いたい場合はIntegerをRealに変更すれば大丈夫です.
# 決定変数の範囲を設定
int1 = Integer(0, 100)
int2 = Integer(0, 50)
problem.types[:] = [int1, int2]
以上のコードをまとめると以下のようになります.
def main():
# 2変数2目的の問題
problem = Problem(2, 2)
# 最小化or最大化を設定
problem.directions[:] = Problem.MINIMIZE
# 決定変数の範囲を設定
int1 = Integer(0, 100)
int2 = Integer(0, 50)
problem.types[:] = [int1, int2]
problem.function = objective
# アルゴリズムを設定し, 探索実行
algorithm = NSGAII(problem, population_size=50)
algorithm.run(1000)
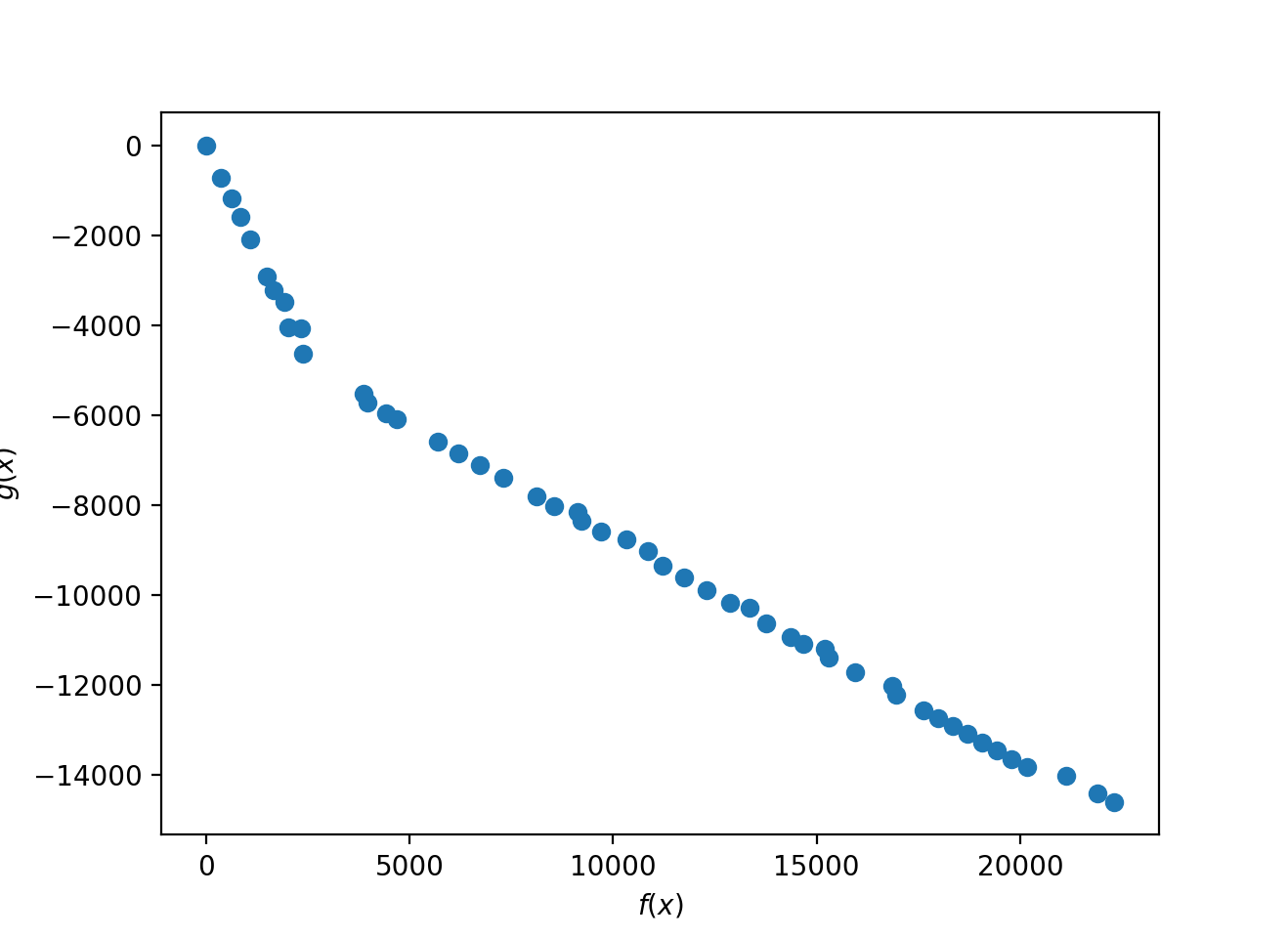
以下のような結果が得られました.
DTLZ2()のような滑らかな曲線ではないですが, パレート最適解を獲得することができました.
ちなみに以下のコードを追加することで, パレート最適解の情報をDataFrameに追加することができます.
df = pd.DataFrame(columns=("x1", "x2", "f1", "f2"))
for i in range(len(nondominated_solutions)):
df.loc[i, "x1"] = int1.decode(nondominated_solutions[i].variables[0])
df.loc[i, "x2"] = int2.decode(nondominated_solutions[i].variables[1])
df.loc[i, "f1"] = nondominated_solutions[i].objectives[0]
df.loc[i, "f2"] = nondominated_solutions[i].objectives[1]
df.to_csv("NSGAII.csv")