まずは、こちらをご覧ください。
See the Pen triangle 01 by Hiroaki Uchiyama (@hirouchi) on CodePen.
上記は、三角関数を使用したアニメーションとなっております。
みなさまは三角関数を使ってアニメーションを作成されておりますでしょうか。
私は全く経験がありませんでしたので、この機会に調査をすることにしました。
なぜ三角関数に興味を持ったのか
私が三角関数と出会ったのは、高校生時代。もう100年も前のお話ですね。(冗談ですね。)
その頃から段々と理系をドロップアウトし文系を選択して、紆余曲折あって今に至ります。
そのような経歴の中で過去に一緒にお仕事をさせていただいた方が、
三角関数を使ったスクロールアニメーションを実装していたことがありました。
当時はフロントエンドエンジニアになったばかりでしたし、
三角関数を使用する理由がわかっておりませんでしたが、ただ漠然と興味を持ちました。
三角関数について
そもそも三角関数とは
そもそも三角関数とは一体何でしょうか。
まずは Wikipedia の情報を見てみましょう。
平面三角法における、角の大きさと線分の長さの関係を記述する関数の族および、それらを拡張して得られる関数の総称である。
(三角関数 - Wikipedia)
すでに私は挫折しそうですが、
角度と線分の長さを表すことができる関数ということでしょうか。
定義法
三角関数には 3 つの定義法があります。
- 直角三角形による定義
- 単位円による定義
- マクローリン展開による定義
今回は、1 と 2 を調べます。
直角三角形による定義
まず、1 つ目の「直角三角形による定義」です。
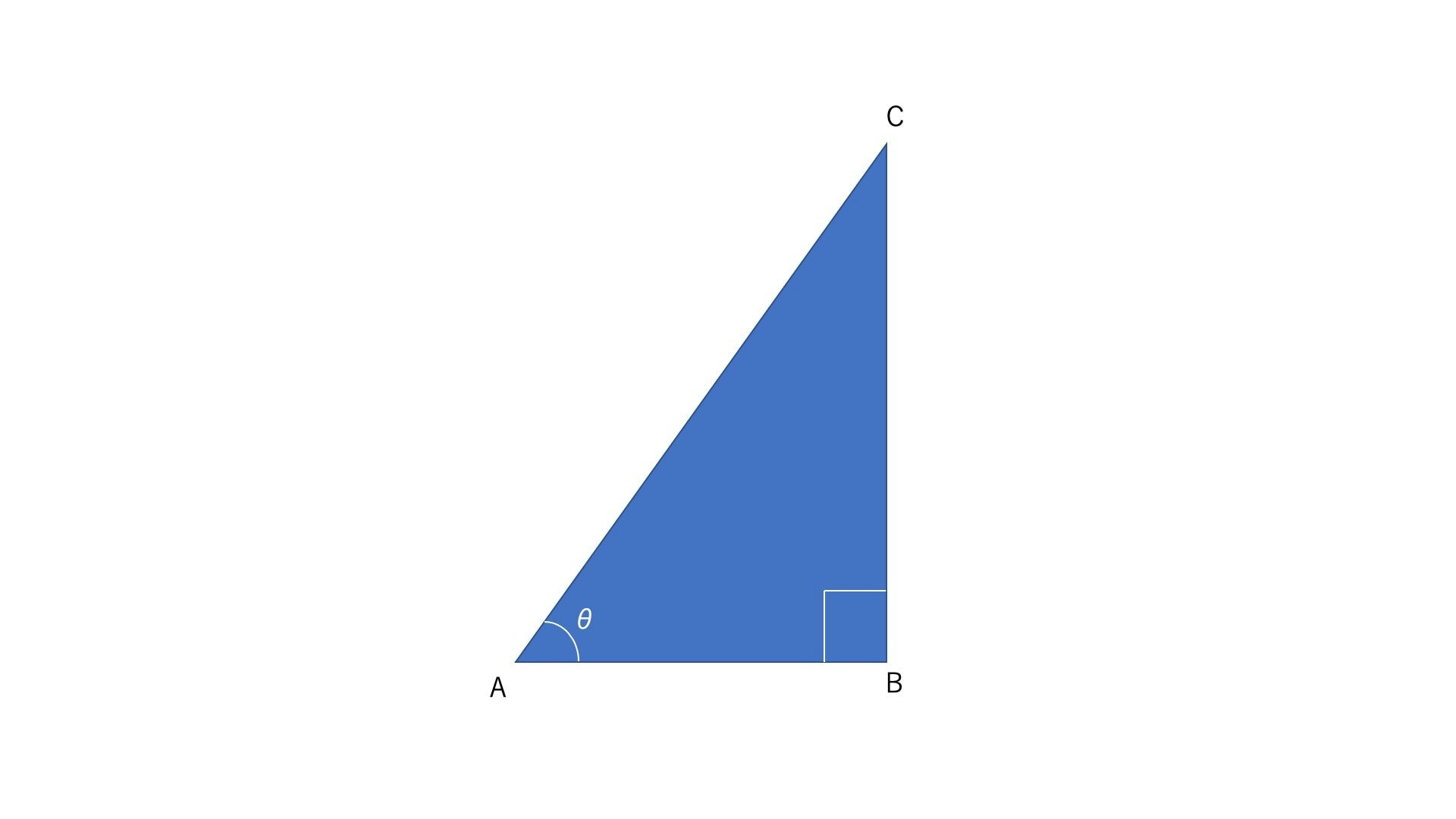
上記の直角三角形を利用し三角関数を定義すると、下記のようになります。
sinθ = \frac{BC}{AC} \\
cosθ = \frac{AC}{BC} \\
tanθ = \frac{BC}{AB}
懐かしいですね!
単位円による定義
高校生時しか三角関数に触れなかった方々は、
1 つ目の定義法が三角関数のイメージなのではないでしょうか。
ただプログラミングでは、こちらの単位円による定義を使用することが多いようです。
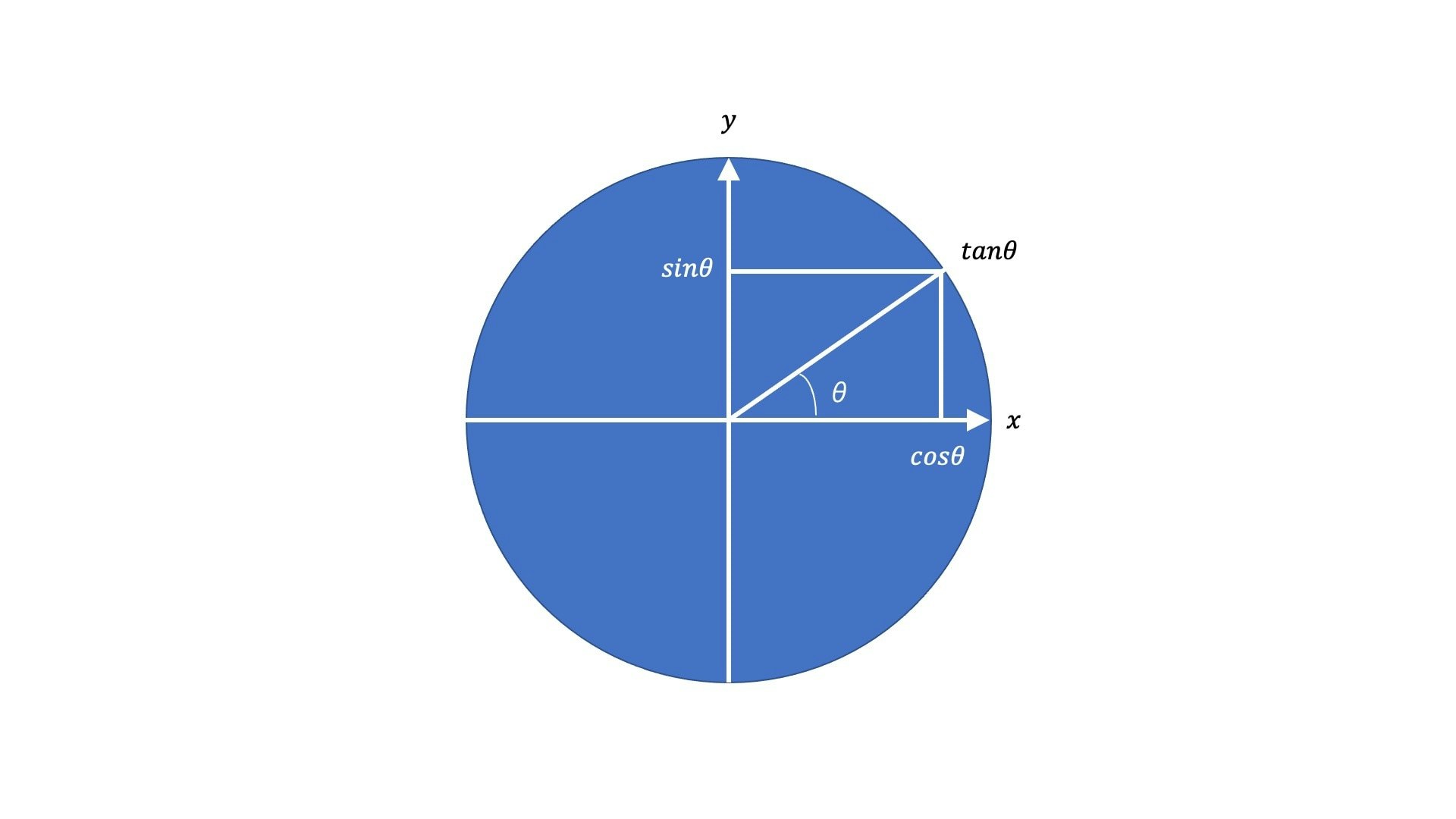
上記の単位円を利用し三角関数を定義すると、下記のようになります。
𝑠𝑖𝑛θ = 単位円上の角度 θ に対応する点の y 座標
𝑐𝑜𝑠θ = 単位円上の角度 θ に対応する点の 𝑥 座標
tanθ = \frac{sinθ}{cosθ}
三角関数使用で何が期待できるか
さて三角関数を軽く復習したところで、なぜ三角関数をアニメーションで使うのかを考えてみましょう。
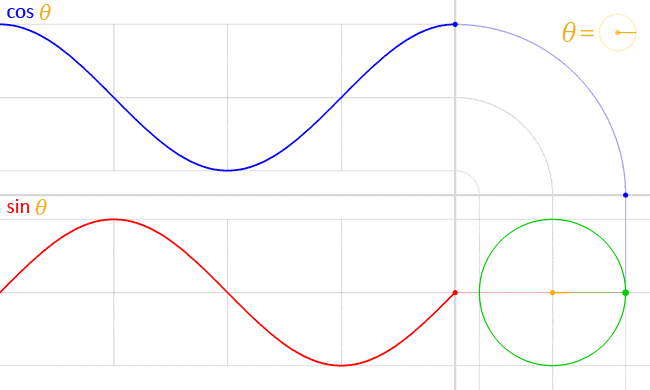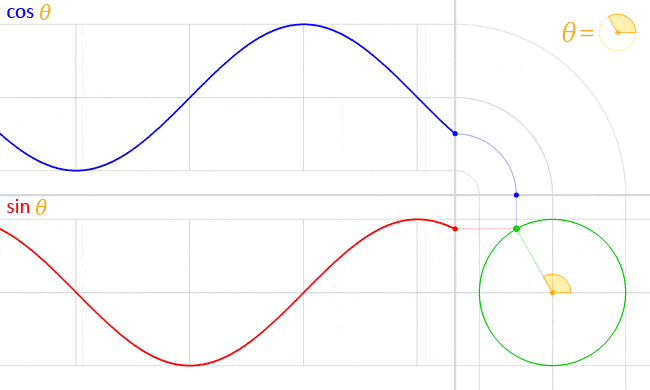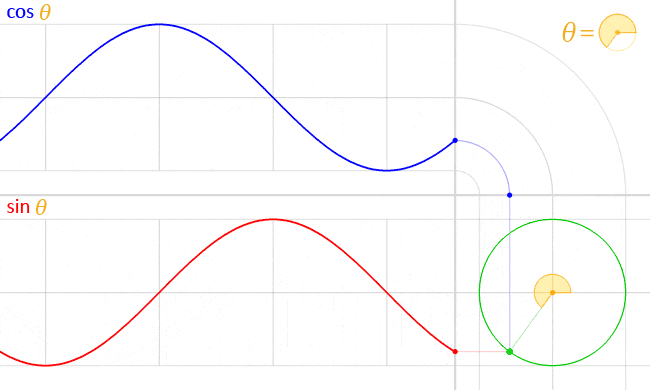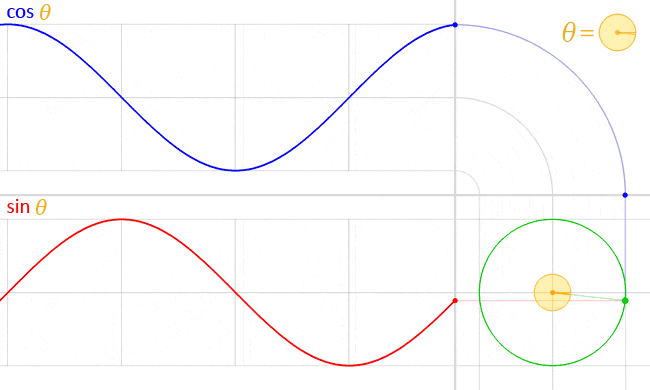
下記は、𝑠𝑖𝑛θ と 𝑐𝑜𝑠θ の単位円上での動きを可視化したものです。
こちらも Wikipedia (三角関数 - Wikipedia) にありました。
図を確認すると滑らかに推移しているのが分かります。
これをアニメーションで利用すると、滑らかに動きそうですね!
実際に作ってみる
さて、やっと最初にお見せしたところまで戻りました。
JavaScript では、
Math.sin(x) // x のサインを返す
Math.cos(x) // x のコサインを返す
Math.tan(x) // x のタンジェントを返す
などの三角関数関連のメソッドがありますので、
これを利用して実装していきます。
円運動を実装
簡単に作ることができました!
See the Pen triangle 02 by Hiroaki Uchiyama (@hirouchi) on CodePen.
ドットが単位円の円周をスムーズに回っていますね。
center で位置調整、radius で円運動大きさを指定してますが、
メインの処理としてはとてもシンプルです。
下記の 2 行で 𝑠𝑖𝑛θ と 𝑐𝑜𝑠θ の値を出力し、
それをドットの position に当てているだけとなります。
const x = center + Math.sin(t) * radius;
const y = center + Math.cos(t) * radius;
三角関数なのに、角度を使わずに getTime() ...。という方もいらっしゃるでしょう。
そのような方には下記のような実装はいかがでしょう。
See the Pen triangle 02-02 by Hiroaki Uchiyama (@hirouchi) on CodePen.
基本的には時間を代入する実装と同じなのですが、
角度の単位をラジアンにしています。
const x = center + Math.sin(radians) * radius;
const y = center + Math.cos(radians) * radius;
ラジアンとは円弧の長さを元にした角度を表す単位で、
変換するとプログラムでの数学的な計算が容易になるとのことです。
(解説しきれず、すみません。三角関数での計算スケールと角度スケールを合わせるイメージでしょうか。)
さいごに
いかがでしたでしょうか、
三角関数の「さ」の字も紹介できていない内容となってしまいましたが、
何ができるか・どのようなメリットがあるか等をフワっと感じていただけたら幸いです。
「理系ドロップアウト経由文系人間の自分でも三角関数を楽しむことができそう」
というのが、私の感想です。
目的などが明確だと学生当時の勉強ももうちょっと捗ったかも...と言い訳もしつつ、
これからは使い所を見つけて実装を試したいなと思いました。
ありがとうございました。