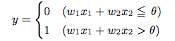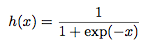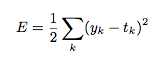はじめに
この記事は、プログラミング初心者かつ、数学や情報系に苦手意識のある文系出身である私が、AIをやりたいと思い「ゼロから作るDeep-Learning」を呼んだあとに理解を深めることを目的として書いたものとなります。
あくまで、この記事は「自身の理解のため」と「苦手なりになんとかアウトプットした」ものとなります。ご了承くださいm(_ _)m ちなみにQiitaも初投稿になります。去年の7月で行ったインターンの成果発表で使用したものをまんま公開してしまおうというものになります。
最後には、XORゲートで簡単な試行錯誤したレポートを書いております。
最初に、やることの確認をします。
- INDEX
- パーセプトロン
- XOR
- ニューラルネットワークと活性化関数
- 多次元配列
- ニューラルネットワークの実装
- 恒等関数
- 学習
- 損失関数
- 勾配
- 学習の実装
- 逆伝播
- レイヤー
- 章ごとのつながり
- BACKPROP実装
15. 学習のテクニック - レポート
1.パーセプトロン
1-1 パーセプトロンの説明
まずは図を。これがパーセプトロン。
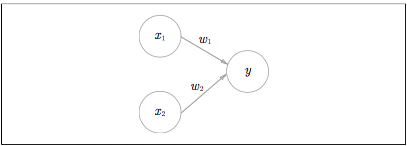
入力信号は、ニューロンに送られる際に、** それぞれに固有の重みが乗算 ** されます。ニューロンでは、送られてきた信号の総和が計算され、その挿話がある限界値を超えた場合にのみ1を出力します。
つまり、重みが大きければ大きいほど、その重みに対応する信号の重要性が高くなる。(値が大きければ大きいほど、大きな信号が流れることを意味する)
1-2 定義の確認
- パーセプトロン
:パーセプトロンとは、複数の信号を入力として受け取り、一つの信号を出力します。 - 重み
:その値が大きければ大きいほど、大きな信号が 流れることを意味します
1-3 パーセプトロンの実装
def AND(x1, x2):
x = np.array([x1, x2])
w = np.array([0.5, 0.5])
b = -0.7
tmp = np.sum(w*x) + b
if tmp <= 0:
return 0
else:
return 1
注目すべき違いがあります。(初見で見落としていたところ)
・重みw1,w2は、入力信号への重要度をコントロールするパラメータとして機能
・バイアスbは、発火(出力信号が1を出力する度合い)を調整するパラメータとして機能します
def OR(x1, x2):
x = np.array([x1, x2])
w = np.array([-0.5, -0.5]) # 重みとバイアスがANDと違う
b = 0.7
tmp = np.sum(w*x) + b
if tmp <= 0:
return 0
else:
return 1
def NAND(x1, x2):
x = np.array([x1, x2])
w = np.array([0.5, 0.5]) # 重みとバイアスがANDと違う
b = -0.2
tmp = np.sum(w*x) + b
if tmp <= 0:
return 0
else:
return 1
上記でわかったことは、AND,OR,NANDは同じ構造で、違いは重みとパラメータの値のみです。
つまり、○のなかには何も入ってなくて、パラメータによってかわるというイメージです。
次にXORゲートを見ていきます。
2. XOR
XORの説明
まずは図を。
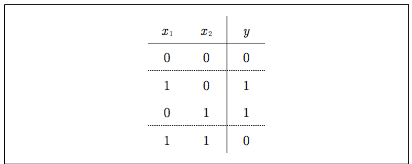
XORゲートは排他的論理和とも呼ばれます。
XORをパーセプトロンで実装するには、重みをどう設定するのかを考えます。
もう一つ図を。
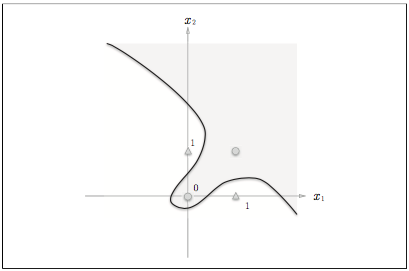
何を示しているかというと、直線(線形)ではXORは分けれないが曲線だとわけれるということです。
つまり、パーセプトロンではXORゲートを表現できません。
しかし、とても重要なことがわかります。
じつは、パーセプトロンの素晴らしさは、層をかさねることができることです・
つまり、層を重ねることでXORを表現できるようになったといえます。
これは先程つかったNANDとORを重ねるとできます。
Pythonで実装してみましょう。
def XOR(x1, x2):
s1 = NAND(x1, x2)
s2 = OR(x1, x2)
y = AND(s1, s2)
return y
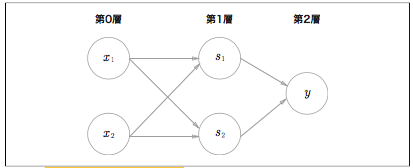
分かりやすかった例が、パイプラインの組み立てで、
1 段目(1 層目)の作業者は流れてくる“部品”に 手を加え、仕事が完了したら 2 段目(2 層目)の作業者に部品を渡します。
2 層目の 作業者は、1 層目の作業者から渡された“部品”に手を加え、その部品を完成させて 出荷(出力)します。
作業者の間で部品の手渡しが行われているようなイメージです。
パーセプトロンのすごい点・できない点
パーセプトロンのすごいところは、複雑な関数を表現できるだけの可能性を秘めていることです。
逆にできないことが大事で、
パーセプトロンができないことは、重みを設定する作業(期待する入力と出力を満たすように適切な重みを決める作業)は、今のところ、人の手によって行われているということです。ANDやORゲートの真理値表を見ながら、私たちが適切な重みを決めまる必要があります。
ニューラルネットワークは、このパーセプトロンができないことを解決するためにあります。
以上でパーセプトロンは終わりです。
パーセプトロンは次に考えるニューラルネットワークの基礎になります。
3. ニューラルネットワークと活性化関数
ニューラルネットワークとパーセプトロンの相違点
復習になりますが、パーセプトロンではバイアスと呼ばれるパラメータで、ニューロンの発火しやすさをコントロールします。
重みを表すパラメータで、これで他の各信号の重要性をコントロールします。
ニューラルネットワークとは、適切な重みパラメータをデータから自動で学習できるというのがニューラルネットワークの重要な性質のひとつとしてあります。
つまり、ニューラルネットワークとパーセプトロンの相違点は、重みを手動でつけるのか、自動でつけるかになります。
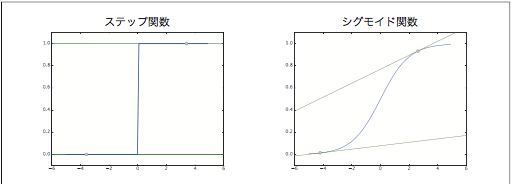
一般的には、「単純パーセプトロン」といえば、単層のネットワークで、活性化関数にステップ関数を使用したモデルのことを指します。「多層パーセプトロン」というと、それは、ニューラルネットワーク(多層で、シグモイド関数などのなめらかな活性関数を使用するネットワーク)を指します。
活性化関数
活性化関数とは、閾値を堺にして出力がきりかわる関数です。
活性化関数がパーセプトロンからニューラルネットワークへ進むためのかけ橋となります。
パーセプトロンは活性化関数にステップ関数を用いているが、それ以外の活性関数を使うことでニューラルネットワークを作れるようになります。
シグモイド関数
なにやら難しそうなので、ステップ関数と比較してみていきます。
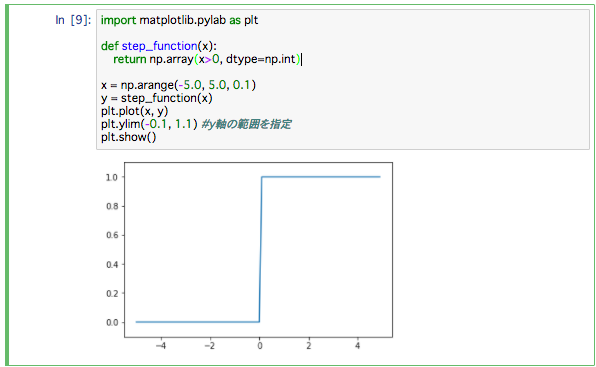
ステップ関数の実装
最初に、ステップ関数とは、入力が0を超えたら1を出力し、それいがは0を出力する関数です。
これを実装すると、
def step_function(x):
if x > 0:
return 1
else:
return 0
単純です。これだとNumpyがつかえないので、書き換えます。
def step_function(x): #Numpy対応版ステップ関数
y = x > 0
return y.astype(np.int)
import numpy as np
x = np.array([-1.0, 1.0, 2.0])
x
y = x > 0
y
出力結果はこちら
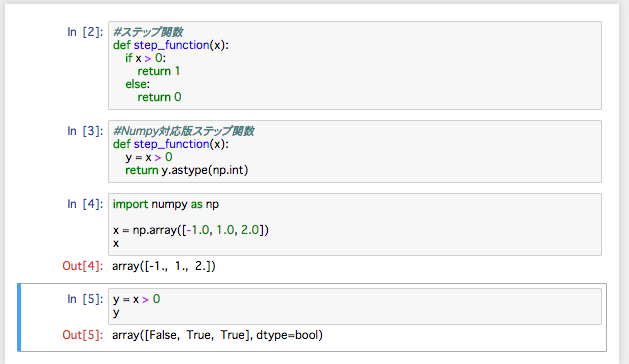
ここでやりたかったことは、ブーリアン型から int 型に変換すると、True が 1 に、 False が 0 に変換されということでSTEP関数をつくります。
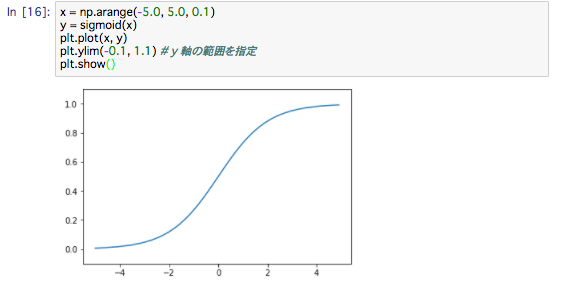
シグモイド関数の実装
def sigmoid(x):
return 1 / (1 + np.exp(-x))
# 試しに値を入れてみる
x = np.array([-1.0, 1.0, 2.0])
sigmoid(x)
シグモイド関数とステップ関数の比較
では、本題、シグモイドとステップの比較。
* 違いは、丸み(滑らかさ)です。
ステップ関数が 0 か 1 のどちらかの値しか返さないのに対して、シグモイド関数は実数――0.731...や 0.880...など――を 返すという点も異なります。
つまり、パーセプトロンではニューロン間を 0 か 1 の二値の信号が流れていたのに対して、ニューラルネットワークでは連続的な実数値の信号が流れます。
この丸みがニューラルネットワークの学習で重要になります。
* 共通点は遠目で見ると似た形をしていることと、非線形関数であることです。
ニューラルネットワークでは、活性化関数に非線形関数を用いる必要があります。裏を返せば、活性化関数には線形関数を用いてはいけないということです。
なぜなら、線形を用いるとニューラルネットワークで層をどんなに増やしても同じことをしている層が存在するということになるからです。
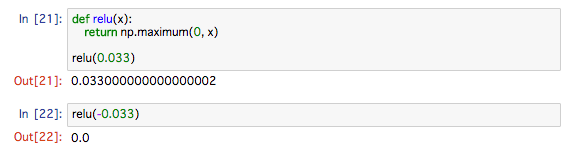
ReLU関数
シグモイドは古くから使われてきましたが、最近はReLU(Rectified Linear Unit)が主に使われます。ReLU は、入力が 0 を超えていれば、その入力をそのまま出力し、0 以下ならば 0
を出力する関数です
数式だと、
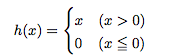
実装は、
def relu(x):
return np.maximum(0, x)
これで活性化関数は終わりです。
次は多次元配列です。
4. 多次元配列
多次元配列とは
多次元配列とは、簡単に言うと数字の集合です。
数字が1列に並んだもの長方形に並べたもの、3時現状に並べたものやN次元上に並べたものを多次元配列といいます。Numpyで作成します。
まずは1次元から

続いて、2次元
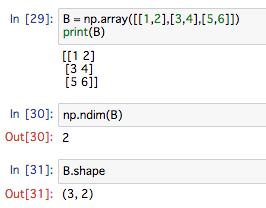
行列とは
新課程でなければ、高校の数学Cで習う行列。
文系の私は当然習ってません(泣)
でも、そんなに難しくないので、初心者でも文系でもいけると思います。
3*2の行列の説明です。
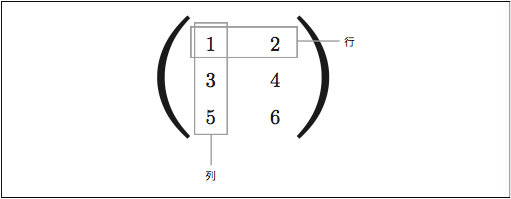
横が行、縦が列
ややこしい…
一番しっくりくる覚え方はこれ

行列の積
まずは図を
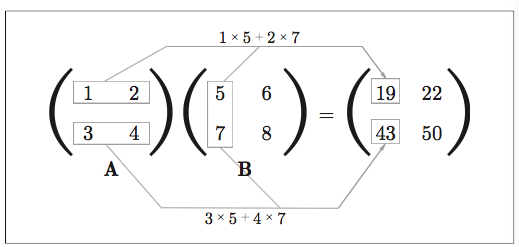
実装すると、

次は、形状の違う行列の計算

ちなみに、エラーが出るとこういうエラー文が出ます
ValueError: shapes (2,3) and (2,2) not aligned: 3 (dim 1) != 2 (dim 0)
こいつに苦しんでましたが、今となれば意外と簡単なことを言っています。
ニューラルネットワークの行列の積
Numpy行列を使ってニューラルネットワークの実装を行っていきます。
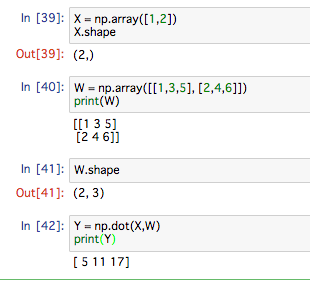
図で見るとこんな感じ。
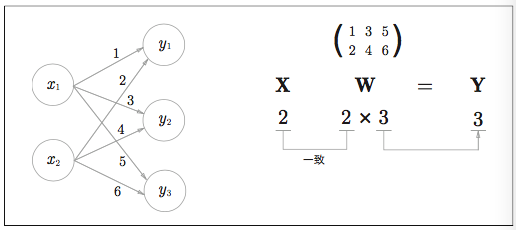
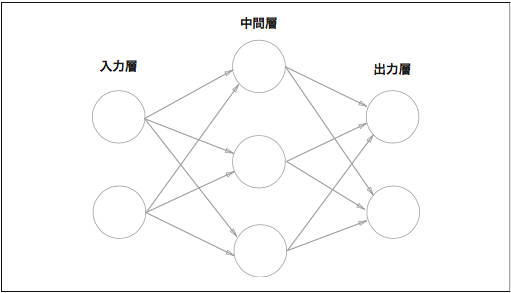
3層ニューラルネットワークの実装
大枠のイメージはこれです。
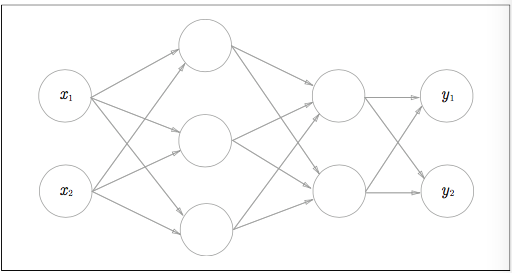
角層ごとに見ていきます。
入力層はこういうイメージ
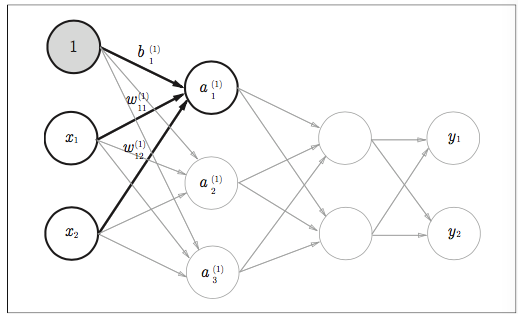
実装はこちら
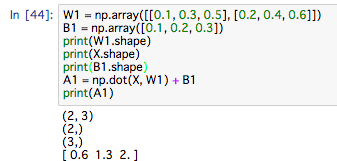
入力層から1層目のイメージ!
X = np.array([1.0, 0.5])
入力層から1層目の実装はこちら
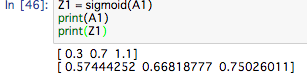
続いて、1層目から2層目の実装
イメージ図
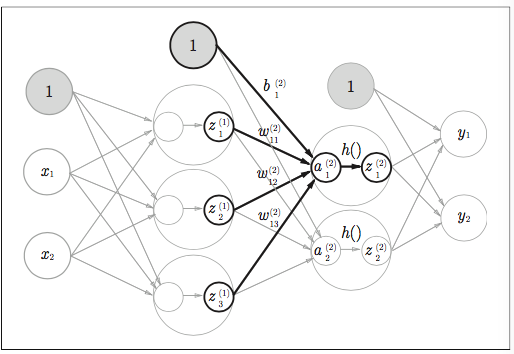
一層目から2層目の実装
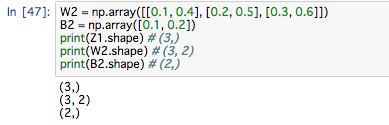
最後に、2層目から出力層のイメージ
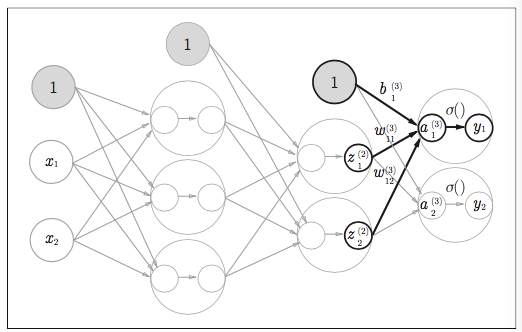
実装はこちら
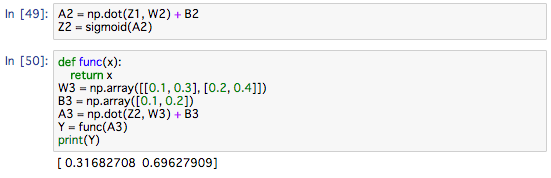
仮にfuncを恒等関数としてます
実装まとめ
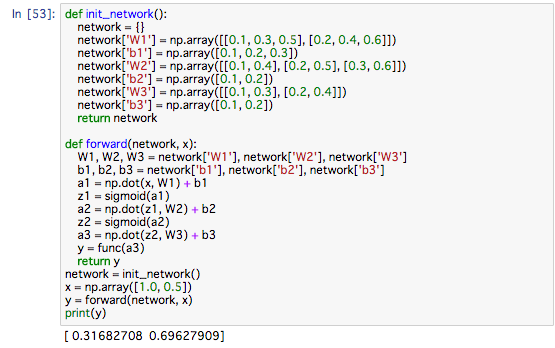
init_net()関数で、重みとバイアスの初期化をおこない、それをディクショナリ型の変数networkに入れます。
forward()関数には、入力信号が出力へと変換されるプロセスがまとめて実装されています。
出力層の設計
ニューラルネットワークは、分類と回帰の両方に用いることができます。
だた、分類か回帰で出力層の活性化関数を変更する必要があります。
一般的に、回帰問題では口頭関数を、分類問題ではソフトマックス関数を使います。
分類問題とは
機械学習は大きく2つあります。
分類問題とは、データが度のクラスに属するかという問題です。
例えば、人の画像からその人が男性か女性かを分類するような問題が分類問題です。
回帰問題とは
回帰問題とは、ある入力データから、連続した数値の予測を行う問題です。
例えば、ヒトの画像から、そのヒトの体重を予測するような問題が回帰問題です。
恒等関数
恒等関数とは、入力をそのまま出力する関数です。
イメージはこちらです
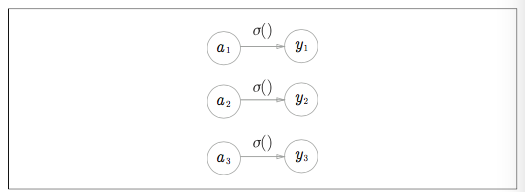
ソフトマックス関数
ソフトマックス関数は分類問題で使われます。
数式でこう表します
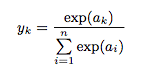
分子は入力信号で指数関数、分母はすべての入力信号の指数関数の和から構成されます
なお、ソフトマックス関数を図で表すと、
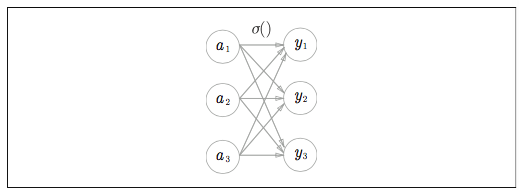
ソフトマックス関数の出力はすべての入力とむすびつきがあります。数式の分母からわかるように出力の各ニューロンがすべての入力から影響を受けることになります。
実装はこうなります
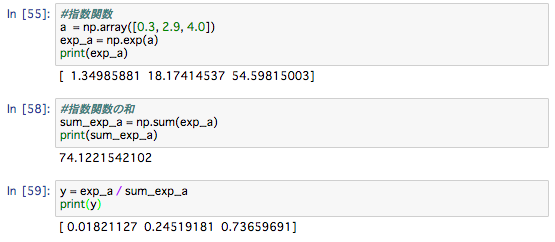
上の実装をまとめたものは

また、ソフトマックスには注意点があって、指数関数なので計算が多く多くなり、PCに負荷がかかる(オーバーフロー)が起こります。
対策としては、

ソフトマックスの特徴
ソフトマックス関数を使えば、ニューラルネットワークのしゅつりょくは 次のように計算することができます。
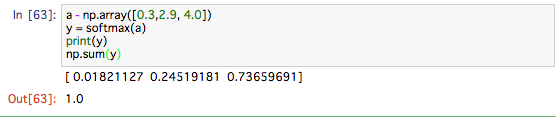
ここで行っているのは、ソフトマックス(以下、SM)の出力は、0から1の間の実数になり、SMの総和は1になります。この性質は非常に重要で、SM関数の出力を 確率として使うことができます。
たとえば、上の例では、y[0]の確率が 0.018(1.8%)、y[1]の確率が 0.245(24.5%)、 y[2]の確率が 0.737(73.7%)のように解釈できます。そして、この確率の結果か ら、「2番目の要素が最も確率が高いため、答えは 2 番目のクラスだ」と言うことができます。さらに、「74%の確率で2番目のクラス、25%確率で1番目のクラス、1%の確率で0番目のクラス」というような確率的な答え方をすることもできます。
ここで、注意点としては 、SM関数を適用しても各要素んお大小関係は変わらないということです。これは、指数関数が単調増加する関数であることに起因する。実際、上の例ではaの要素の大小関係とyの要素の大小関係は変わっていません。例えば、aの最大値は2番めですが、yの最大値も2番めです。
ニューラルネットワーク(以下、NN)のクラス分類では、一般てきに、出力の一番大きいニューロンに相当するクラスだけを認識結果とします。そして、SM関数を適用しても、出力の一番大きいニューロンのばしょは変わりません。
そのため、NNが分類を行う際には、出力層のSMを省略することができます。実際の問題では、指数関数の計算は結構PCの計算が必要となりますので、出力そのSM関数は称するのが一般的です。
学習と推論
機械学習の問題を解く手順は学習と推論の2つに手順がわけれます。
最初に、 学習 でモデルの学習をおこない、推論で学習したモデルをつかって道のデータに対して推論(分類)を行います。
推論の手順ではソフトマックス関数は省略するのが一般です。
出力層にSM関数を用いる理由はNNの学習時に関係してきます。
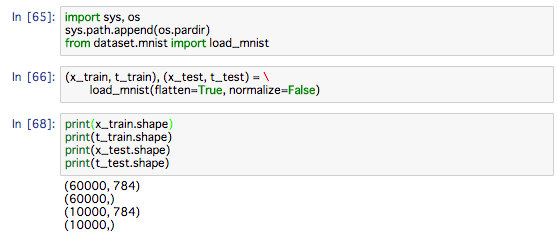
5. ニューラルネットワークの実装
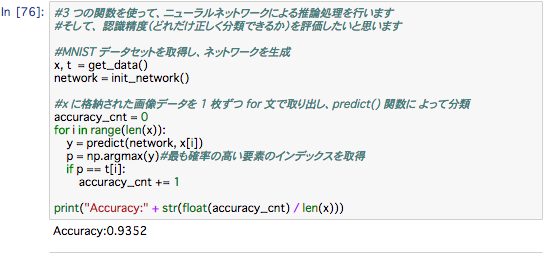
実践問題として手書き数字画像の分類を行います。
学習をすでに完了したものとして、学習済みのパラメータを使って、推論処理を実装していきます。
引数として、 load_mnist(normalize=True, flatten=True,one_hot_label=False)のように、3 つの引数を設定することができます。
ひとつ目の引数である normalize は、 入力画像を 0.0~1.0 の値に正規化するかどうかを設定します。これを False にすれば、入力画像のピクセルは元の 0~255 のままです。2 つ目の引数の flatten は、入力画像を平らにする(1 次元配列にする)かどうかを設定します。False に設定すると、入力画像は 1 × 28 × 28 の 3 次元配列として、True にすると 784 個の要素からなる 1 次元配列として格納されます。3 つ目の引数の one_hot_label は、ラベルを one-hot 表現として格納するかどうかを設定します。one-hot 表現とは、たとえば [0,0,1,0,0,0,0,0,0,0] のように、正解となるラベルだけが 1 で、それ以外 は 0 の配列です。one_hot_label が False のときは、7、2 といったように単純に 正解となるラベルが格納されますが、one_hot_label が True のときは、ラベルは one-hot 表現として格納されます。
MNISTを表示させてみることにします。
画層の表示にはPILモジュールを使用します。
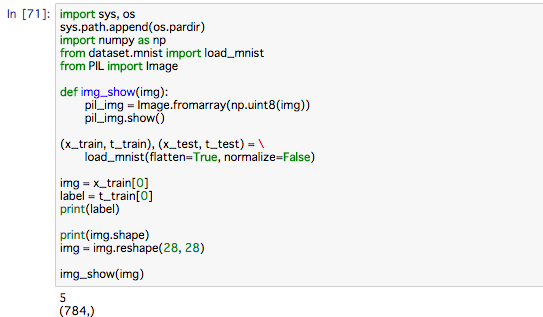
実行するとこの画像が表示されます。

ここでの注意点はflatten=Trueとして読み込んだ画像はNumpy配列としてイジゲンで格納されているということです。そのため画像の表示に際しては、元の形状である28*28にreshapeする必要があります。
Image.fromarray() は NumPy として格納された画像データを、PIL 用のデータオブジェクトに変換します。
では、本題の推論処理を行うNNの実装をしていきます。
ネットワークは入力層を784個、出力層を10個、隠れ層が2つあり、50個の層と、100個のニューロンを持つもので構成します。
コードを実行すると、「Accuracy:0.9352」と表示されます。これは、
93.52% 正しく分類することができたことを表しています。
load_mnist 関数の引数である normalize には True を設定しました。normalize を True に設定すると、その関数の内部では画像の各ピクセルの値を 255 で除算し、データの値が 0.0~1.0 の範囲に収まるように変換されます。 このようなデータをある決まった範囲に変換する処理を正規化(normalization)と言います。また、ニューラルネットワークの入力データに対して、何らかの決まった変換を行うことを
前処理(pre-processing)と言います。
ここでは、入力画像データに前処理として正規化を行ったことになります。
ニューラルネットワークにおいて、よく前処理は使われます。
データ全体の分布の計上をチンイツにすると行った方法を白色化といいます。
NNの実装は以上です。
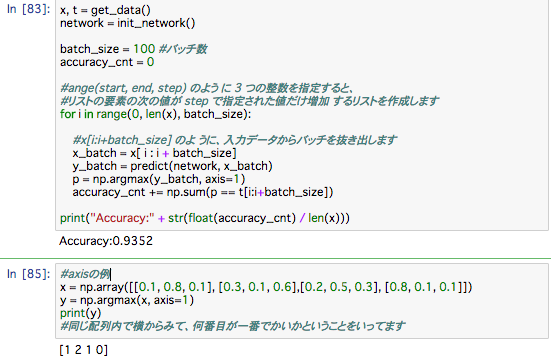
バッチ処理
入力データと重みパラメータの形状に注意して、先程の実装を再度見ていくことにします。
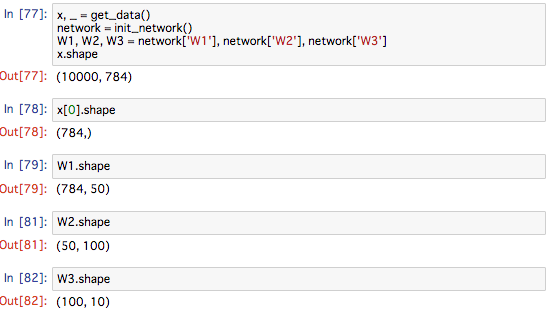
図で見ると、
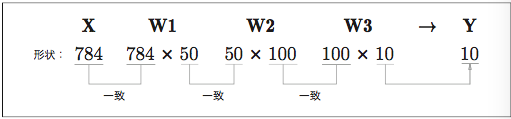
まとまりのある入力データをバッチ(batch)と呼びます。
バッチ処理によって、1 枚あたりの処理時間を大幅に短縮できるという利点です。なぜ処理時間を短縮できるかというと、数値計算を扱うライブラリの多くは、大きな配列の計算を効率良く処理できるような高度な最適化が行われています。
バッチ処理を行うことで大きな配列の計算を行うことになりますが、大きな配列を一度に計算するほうが、分割した小さい配列を少しずつ計算するよりも速く計算が完了するのです。
axis=1という引数は、100 * 10 の配列の中で1次元目の要素ごとに(1次元目を軸として)、最大値のインデックスを見つけることをしています(0次元目は最初のじげんに対応します)
np.array(行、列)があって、axis=0で行を指定、axis=1で列を指定できる
以上でニューラルネットワークの順伝搬は終わりです。
まとめとしては、パーセプトロンと、ニューロンの信号が階層的に伝わる事が大事です。
次のニューロンへ信号を送る際に、信号を変化させる活性化関数に大きな違いがあり、シグモイド関数を使います。ステップ関数とシグロイド関数の違いが重要になってきます。次に見ていきます。
要点
*NNではシグモイド関数やReLU関数を使って滑らかに変化するようする
*機械学習の問題は、回帰問題と分類問題に大別できる
*出力層で使用する活性化関数は、回帰問題では恒等関数、分類問題ではソフトマックス関数を一般的に利用する
*分類問題では、出力層のニューロンの数を分類するクラス数に設定する
7. 学習
前提として学習とは、訓練データから最適な重みパラメータの値を自動で獲得することを指します。
損失関数を基準として、その値が最も小さくなる重みパラメータを探し出すための手法として、勾配法と呼ばれる、関数の傾きを使った手法を使います。
この章で説明するのは、
*損失関数
*勾配です。
データから学習する
ニューラルネットワークの特徴は、データから学習できる点です。
層を深くすれば、重みパラメータの数も億を超えるので、自動で決めれることは非常に有効です。
その方法を試していきます。
データ駆動
機械学習はデータが命です。
ヒトとの違いは、問題を解決しようとするとき、経験から試行錯誤するのですが、
機械学習はデータからパターンを見つけようとします。
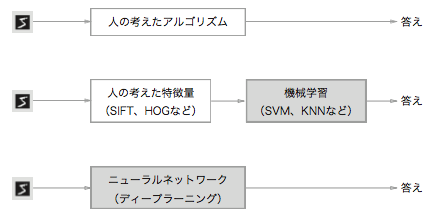
画像の識別の場合、特徴量を抽出します。
画像の特徴量は通常、ベクトルとして記述されます。なお、コンピュータビジョンの分野で有名な特徴 量としては、SIFT や SURF、HOG などが挙げられます。そのような特徴量を使って画像データをベクトルに変換し、その変換されたベクトルに対して、機械学習で使われる識別器―― SVM や KNN など――で学習させることができます。
この機械学習によるアプローチでは、集められたデータの中から「機械」が規則性を見つけ出します。これは、ゼロからアルゴリズムを考え出す場合に比べると、より 効率的に問題を解決でき、「人」への負担も軽減されるでしょう。ただし、画像をベクトルに変換する際に使用した特徴量は、「人」が設計したものであることに注意が必要です。
簡潔に言うと、特徴量と機械学習によるアプローチでも問題に応じて、ヒトの手によって適した特徴量を考える必要があるかもしれないです。
また、NNの利点は、すべての問題を同じ流れで解くことができる点にあります。
簡潔に言うと、NNは、対象とする問題に関係なく、データをそのままの生データとして、端から端まで(end-to-end)で学習することができます。
訓練データとテストデータ
機械学習におけるデータの取扱についての注意点は、
*訓練データ:まずは訓練データだけを使って学習を行い、最適なパラメータを探索します。
*テストデータ:テストデータを使って、訓練したモデルの実力を評価します
の2つのデータに分けて、学習や実験などを行うのが一般的です。
なぜ分けるかというと、ニューラルネットワークに求めるのはモデルの汎用的な能力であるからです。この汎化能力を正しく評価したいがために、分けてます。
機械学習の最終的な目標はこの汎化能力です。
損失関数
ニューラルネットワークの学習で用意られる指標は、損失関数と呼ばれます。
損失関数には、2条和誤差や交差エントロピー誤差が用いられます。
損失関数はニューラルネットワークの性能の悪さを示す指標です。
現在のニューラルネットワークが教師データに対してどれだけ適合していないか、教師データに対してどれだけ一致していないかということを示します。
性能の悪さはマイナスをかければ、どれだけ性能がいいかという指標になります。
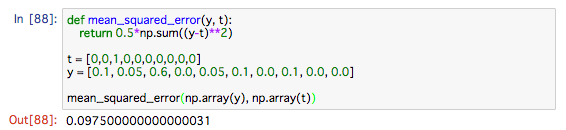
2乗和誤差
例で見ましょう
y = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]
t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
yは「0」の確率は 0.1、「1」の確率は 0.05、「2」の確率は 0.6 といったようなことを表しています。
tは正解となるラベルを 1、それ以外を 0 とします。ここではラベルの「2」が 1 なので、正解は「2」であることを表しています。なお、この表記法をone-hot表現といいます。
損失関数は小さいほうが教師データとの誤差が小さいことがわかります
交差エントロピー誤差
まずは数式、
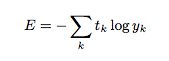
実装では以下のように示します。
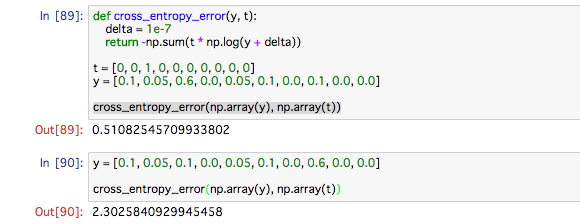
logの計算時に、微小な値であるdeltaをたして、np.log(0)のような計算が発生した場合、それ以上計算をマイナスに無限大に進むのを防いでます。
ミニバッチ学習
機械学習の問題は、訓練データを使って学習を行います。
訓練データを使って学習するとは、正確に言うと、
訓練データにたいする損失関数を求め、その値をできるだけ小さくするようなパラメータを探し出すと言うことです。
そのため、損失関数は、すべての訓練データを対象として求める必要があります。
例えば、訓練データが100あったら、その100この損失関数の和を指標とするのです。
数式ではこう書くことができます。
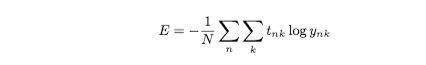
Nで割って正規化しています。このNで割ることによって、1個あたりの「平均の損失関数」を求めることになります。そのように平均化すれば、訓練データの数に関係なく、いつでも統一した指標が得られます。たとえば、訓練データが1,000個や10,000個の場合であっても、1個あたりの平均の損失関数を求められます。
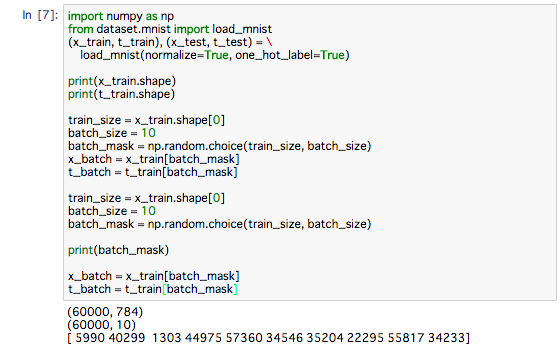
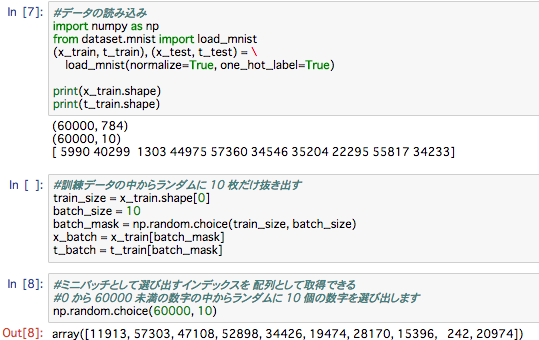
MNIST データの読み込みによって、訓練データは 60,000 個あり、入 力データは 784 列(元は 28 × 28)の画像データであることが分かります。また、教 師データは 10 列のデータです。そのため、上の x_train、t_train の形状は、それ ぞれ (60000, 784)、(60000, 10) になります。
60,000 枚の訓練データの中から 100 枚を無作為に選び出して、その 100 枚を使って学習を行うのです。 このような学習手法をミニバッチ学習と言います。
データがひとつの場合と、データがバッチとしてまとめられて入力される場合の両方のケースに対応するように実装します
教師データがラベルとして与えられたとき(one-hot 表現ではなく、「2」や 「7」といったラベルとして与えられたとき)、交差エントロピー誤差は次のように実装することができます。
バッチ対応版 交差エントロピー誤差の実装
実装のポイントは、one-hot 表現で t が 0 の要素は、交差エントロピー誤差 も 0 であるから、その計算は無視してもよいということです。言い換えれば、正解ラベルに対して、ニューラルネットワークの出力を得ることができれば、交差エントロピー誤差を計算することができるのです。そのため、t が one-hot 表現のときは t * np.log(y) で計算していた箇所を、t がラベル表現の場合は、 np.log( y[np.arange(batch_size), t] ) として、同じ処理を実現します。
なぜ損失関数を設定するのか
認識精度を指標にせず、なぜ損失関数を導入するのか。
それは、学習における「微分」の役割があるからです。
ニューラルネットワークの学習では、最適なパラメータ(重みとバイアス)を探索する際に、損失関数の芭蕉を探すために、パラメータの微分(正確には勾配)を計算し、その微分の値を手がかりにパラメータの値を徐々に更新していきます。
重みパラメータの損失関数に対する微分はその重みパラメータの値を少しだけ変化させたときに、損失関数がどのように変化するかを示します。
微分の値が 0 になると、重みパラメータをどちらに 動かしても、損失関数の値が変わらないため、その重みパラメータの更新はそこでストップします。
なので、ニューラルネットワークの学習の際に、認識精度を“指標”にしてはいけない。 その理由は、認識精度を指標にすると、パラメータの微分がほとんどの場所で 0 になってしまうからである。
ステップ関数とシグモイド関数も一緒です。微分(接線)は連続的に変わっています。
9. 勾配
数値微分
勾配の話をする前にまずは微分から。
微分と は、「ある瞬間」の変化の量を表したものです。
どんどん時間を小さくすることで、ある瞬間の変化の量(ある瞬間の速度)を得ることができるようになります。
数式ではこう表します。
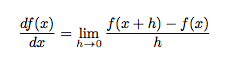
左辺の df(x)/dx は、f(x) の x についての微分―― x に対する f(x) の変化の度合い――を表す記号です。
数値微分
微小な差分によって微分を求めることを数値微分 (numerical differentiation)といいます。
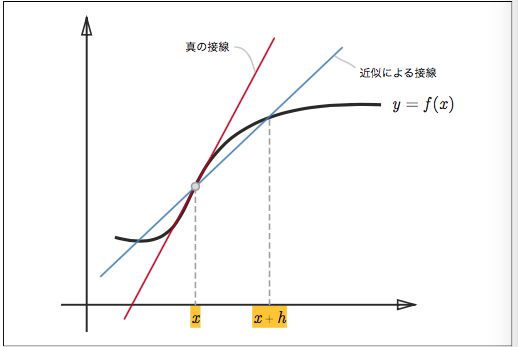
(x + h) と (x − h) での関数 f の差分を計算することで、誤差を減らすことがで きます。この差分は、x を中心として、その前後の差分を計算することから、中心差 分と言います(一方、(x + h) と x の差分は前方差分と言います)
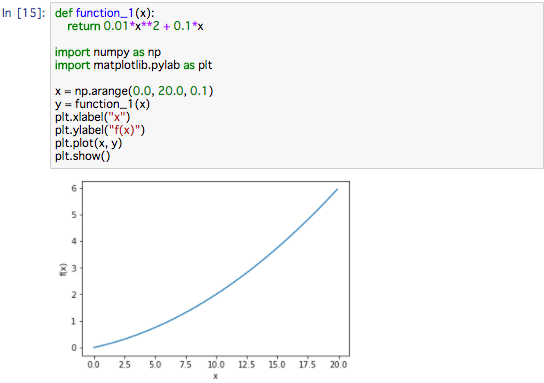
数値微分の例
簡単な関数を微分してみます。
y = 0.01x**2 + 0.1x
def function_1(x):
return 0.01 * x ** 2 + 0.1 * x
偏微分
先程の微分と違うのは変数が2つあることです。
数式ではこう書きます
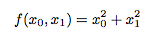
実装するとこうです。
def function_2(x):
return x[0]**2 + x[1]**2````
図ではこうです。

2 つある変数のどちらの変数に対しての微分かということを区別する必要があります。
ですので、このように実装します。

変数がひとつだけの関数を定義して、その関数について微分を 求めるような実装を行っています
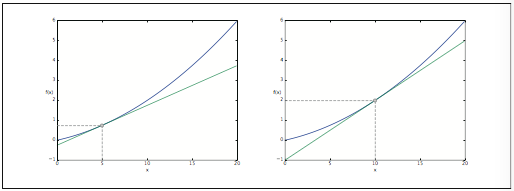
問 1 の答えは 6.00000000000378、問 2 の答えは 7.999999999999119 になりました。これは、解析的な微分の解とほぼ一致します。
このように、1変数の微分と同じで、ある場所の傾きを求めます。
違いは、偏微分の場合、複数ある変数の中でターゲットとする変数をひとつに絞り、他の 変数はある値に固定します。
先の例では、x0 と x1 の偏微分の計算を変数ごとに計算しました。
まとめて計算したいときを考えます。
たとえば、x0 = 3、x1 = 4 のときの
(x0, x1) の両方の偏微分をまとめて、 ∂f/∂x0 , ∂f/∂x1 として計算することを考えましょう。なお、 ∂f/∂x0 , ∂f/∂x1 のように、すべての変数の偏微分をベクトルとしてまとめたものを勾配(gradient)と言います。勾配は、たとえば、次のように実装することが
できます。

やっていることは、1変数の数値微分と殆ど変わりません。
実際に計算してみました。

このように、(x0, x1) の各点における勾配を計算することができます。上の例で は、点 (3, 4) の勾配は (6, 8)、点 (0, 2) の勾配は (0, 4)、点 (3, 0) の勾配は (6, 0) と いったような結果になりましたが、この勾配は何を意味しているのでしょうか? そ れを理解するために、f (x0 , x1 ) = x20 + x21 の勾配を図で表してみることにしました。ここでは勾配の結果にマイナスを付けたベクトルを描画します。

勾配は一番低い場所を指しましたが、実際は必ずしもそうなるとは限りません。
しかし、勾配は各地点に置いて低くなる方向を指します。
もっと正確に言うと、勾配が示す方向は各場所において**関数の値を最も減らす方向**です。
##### 勾配法
機械学習の問題の多くは、学習の際に最適なパラメータを探索します。ニューラルネットワークも同様に最適なパラメータ(重みとバイアスを)学習時に見つけなければなりません。
ここで、最適なパラメータと言うのは、**損失関数が最小値を取るときのパラメータの値**です。
しかし、損失関数は複雑ですので、パラメータ空間は広くて、どこに最小値をとる場所があるのか見当がつきません。そこで、勾配をうまく利用して関数の最小値(できるだけ小さい値)を探そう、というのが勾配法です。
注意点は、各地点において関数の値を最も減らす方向を示すのが勾配だと言うことです。その為、勾配が指す先が本当に関数の最小値なのかどうか、また、その先が本当に進むべき方向なのかどうか保証できません。
実際、複雑な関数において、勾配が指す方向は、最小値ではない場合がほとんどです。
関数の極小値や最小値または鞍点(saddle point)と呼ばれる場所では、勾配が0になります。
極小値は、局所的な最小値、つまり、ある範囲に限定した場合に呑み最小値になる点です。
また、鞍点とは、ある方向で見れば極大値で、別の方向で見れば極小値となる点です。勾配法は勾配が0の場所を探しますが、それが必ずしも最小値だとは限りません。
関数が複雑な形だとtairaな所にはまり、学習が進まない停滞期(プラトー)に陥る事があります。
勾配が絶対に最小値の場所を示すわけではないにしろ、その方向に進むことで関数の値を最も減らさせることができます。
そのため、最小値の場所を探す問題に於いては、勾配の情報を手がかりに、進む方向を決めるべきで、ここで勾配法が有効です。
勾配法は、現在の場所から勾配方向に一定の距離だけ進みます。
そして、移動した先でも同様に勾配を求め、また、その勾配方向へ進むというように、繰り返し勾配方向へ移動します。
このように勾配方向へ進むことを 繰り返すことで、関数の値を徐々に減らすのが勾配法と言います。
勾配法は機械学習の**最適化問題**でよく使われる手法です。
特に、ニューラルネットワークの学習ではよく勾配法が用いられます。
最小値を探す場合、勾配降下法といいます。
数式では、

η は更新の量を表します。これは、ニューラルネットワークの学習においては、学習率(learning rate)と呼ばれます。
**1 回の学習で、どれだけ学習すべきか、どれだけパラメータを更新するか**、ということを決めるのが学習率です。
つまり、ステップごとに、式 (4.7) のように変数の値を更新していき、そのステップを何度か繰り返すことによって徐々に関数の値を減らしていくのです。
学習率の値は、まえもって決める必要があります。
学習率は大きすぎても小さすぎても、いい場所にたどり着くことはできません。
ニューラルネットワークの学習においては、学習率の値を変更しながら、正しく学習できているかどうか、確認作業を行うのが一般的です。
では、勾配降下法を実装してみます。

引数の f は最適化したい関数、init_x は初期値、lr は learning rate を意味する学習率、step_num は勾配法による繰り返しの数です。
試しに、問題をときます。
問:f (x0 , x1 ) = x20 + x21 の最小値を勾配法で求めよ。

ここでは、初期値を (-3.0, 4.0) として、勾配法を使って最小値の探索を開始 します。最終的な結果は (-6.1e-10, 8.1e-10) となり、これはほとんど (0, 0) に近い結果です。
図で示すと、

試しに、学習率をちいさくしてみると

値が更新されず、適切な学習を設定できません。
学習率のようなパラメータはハイパーパラメータといいます。
これは、ニューラルネットワークの重みとは異なる性質です。
重みは訓練データと学習アルゴリズムに寄って自動で獲得されるのにたいし、学習率のようなハイパーパラメータは人の手によって設定されるパラメータです。
実際には、で作業でハイパーパラメータを試しながら、うまく学習できるケースをさがすという作業が必要です。
##### ニューラルネットワークに対する勾配
NNにおける勾配とは、重みパラメータに関する損失関数の勾配です。
例えば、数式だと

∂L/∂wの各要素は、それぞれの要素に関する偏微分から構成されます。
たとえば、1 行 1 列目の要素である ∂L/∂w11 は、w11 を少し変化させると損失関数 L がどれだけ変化するか、ということを表します
大切な点は、∂L/∂Wの形状はWと同じであるということです。上の式は2*3で同じ形状です。
##### ニューラルネットワークでの勾配の実装
今回は、simpleNetというクラスで実装します。

形状が2*3の重みのパラメータをひとつだけインスタンス変数として持ちます。
続いて勾配を求めてみましょう。
numerical_gradient(f, x)を使って勾配を求めます。f(x)はダミーの引数です

w11 を h だけ増やすと損失関数の値は -0.25h だけ増加するということを意味します
マイナス方向なので、プラス方向に更新した方がいいことがわかります。また、値が大きい方が更新の度合いについても大きく貢献するということがわかります。
ニューラルネットワークの勾配を求めれば、あとは勾配法に従って、重みパラメータを更新するだけです。次節では、2層のニューラルネットワークを学習していきます。
### 10. 学習の実装
#### 学習アルゴリズムの実装
ニューラルネットワークの学習についての知識は一通り触れました。
損失関数、ミニバッチ、勾配、勾配降下法の復習を兼ねて学習の手順を確認することにします。
*前提
ニューラルネットワークは、適応可能な重みとバイアスがあり、この重みとバイアスを訓練データに適応するように調整することを学習と呼ぶ学習は4つの手順で行う。
*1.ミニバッチ
訓練データの中からランダムに一分のデータを選び出す。その選ばれたデータをミニバッチといい、ここでは、そのミニばちの損失関数の値を減らすことを目的とする
*2.勾配の算出
ミニバッチの損失関数を減らすために、各重みのパラメータの勾配を求める。勾配は、損失関数の値を最も減らす方法を示す。
*3.パラメータの更新
重みパラメータを勾配方向に微小量だけ更新する
*4.繰り返す
勾配降下法によってパラメータを更新する方法ですが、ミニバッチとして無作為に選ばれたデータを使用していることから、確率的勾配降下法(stochastic gradient descent)略してSDGと呼ばれます。
確率的に無作為に選びだしたという意味です。
2層のニューラルネットワークを作っていきます。

paramsとgradsというディクショナリ変数があります。
params['W1']に重みが格納されています。
ほかも見ましょう

上のようにparams変数には、このネットワークに必要なパラメータがすべて格納されています。そして、params変数に格納された重みが、推論処理で使われるます。ちなみに推論処理は次のように実行できます。

また、grads変数には、params変数と対応するように、各パラメータの勾配が格納されます。例えば、次に示すように、numerical_gradient()メソッドを使って勾配を計算すると、grads変数に勾配情報が格納されます。

__init__メソッドでは、入力画像サイズが 28 × 28 の計 784 個あり、出力は 10 個のクラスになります。そのため、引数の input_size=784、output_size=10 と指定し、 隠れ層の個数である hidden_size は適当な値を設定します。
この初期化メソッドでは、重みパラメータの初期化を行います。重みパラ メータの初期値をどのような値に設定するかという問題は、ニューラルネットワー クの学習を成功させる上で重要です。後ほど、重みパラメータの初期化について 詳しく見ていきますが、ここでは、重みはガウス分布に従う乱数で初期化し、バイ アスは 0 で初期化します。
numerical_gradient(self, x, t) は、数値微分によってパラメータ の勾配を計算します。次章では、この勾配の計算を高速に求める誤差逆伝搬方について説明します。
誤差逆伝播法を使って求めた勾配の結果は、数値微分による結果とほぼ同じになりますが、高速に処理することができます。
##### ミニバッチ学習の実装
ニューラルネットワークの学習の実装は、前に説明したミニバッチ学習で行います。
ミニバッチ学習とは、訓練データから無作為に一分のデータを取り出して、勾配法によりパラメータを更新します。

ここでは、ミニバッチのサイズを100として、60000個の訓練データからランダムに100このデータ(画像データと正解データ)を抜き出していきます。
そして、その100個のミニバッチを対象に勾配を求め、確率勾配降下法によりパラメータを更新しています。
ここでは、勾配法による更新の回数(繰り返し回数(iteration))を10000回として、更新するごとに、訓練データに対する損失関数を計算し、その値を配列に追加します。この損失関数の値の推移をグラフで表すと以下のようになります。

学習の回数が進むに連れて、損失関数の値がへっているので学習がうまくいっている証拠になります。
##### テストデータで評価
訓練データのミニバッチに対する損失関数の値です。
ニューラルネットワークの学習では、過学習を起こしていないかを確認します。
過学習とは、例えば、訓練データに含まれる数字画像だけは正しく見分けられるが、訓練データに含まれない数字画像は識別できないと言うことを意味します。
ニューラルネットワークの学習の目標はそもそも、汎化能力を身につけることです。そのため、ニューラルネットワーク評価をするには、訓練データに含まれないデータを使って評価しなければいけません。今から、学習を行う過程で、定期的に訓練データとテストデータを対象に、認識精度を記録することにします。ここでは1エポックごとに、訓練データとテストデータの認識精度を記録することにします。
エポック(epoch)とは単位を表します。1エポックとは**学習において訓練データをすべて使いきったときの回数**に対応します。ミニバッチが100個デあれば、確率的勾配降下法を100回繰り返したら、1エポックとなります。

1エポックごとに、すべての訓練データとテストデータに対して認識精度を計算して、その結果を記録します。なぜ1エポックごとに認識精度を計算するかというとfor文の繰り返しの中で非常に認識精度を計算していては時間がかかってしまうからです。そしてざっくり認識精度の数がわかればよいのです。
グラフにするとこうなります。

エポックが進むにつれて、認識精度は向上していることがわかります。また、2つの線に誤差がないので過学習が起きてないこともわかります。
#### まとめ
ニューラルネットワークの学習について説明しました。
流れは、始めに学習を行えるように損失関数という指標を導入しました。
この損失関数を基準として、その値が最も小さくなる重みパラメータを探し出すことが目標です。
また、できるだけ小さな損失関数の値を探し出すための手法として、勾配法と呼ばれる、関数の傾きを使った手法を説明しました。
* 機械学習で使用するデータは訓練データとテストデータに分ける
* 訓練データで学習し、テストデータで汎化能力を評価する
* ニューラルネットワークの学習は損失関数を指標として、損失関数の値が小さくなるように、重みパラメータを更新する
* 重みパラメータを更新する際には、重みパラメータの勾配を利用して、勾配方向に重みの値を更新する作業をくりかえす
* 微小な値を与えたときの差分によって微分を求めることを数値微分という
* 数値部分によって重みパラメータの勾配を求めることができるが、誤差逆伝搬法のほうが高速に求めれる
***
### 11. 誤差逆伝播法
#### 連鎖率とは
まず合成関数から説明します。
合成関数とは、複数の関数によって構成される関数のことです。
連鎖率とは合成関数の微分についての性質であり、次のように定義します。
ある関数が合成関数で表される場合、その合成関数の微分は、合成関数を構成するそれぞれの関数の微分の積によって表すことができる。
これを連鎖率の原理といいます。
数式で見るとこうです。

計算グラフにすると

図のように、逆伝播は右から左へと流れます。
ノードへの入力信号に足して、ノードの局所的な微分(偏微分)を乗算して次のノードへと伝搬していきます。
#### 逆伝搬
逆伝搬の仕組みを見ていきます。
##### 乗算ノードの逆伝搬
加算ノードはそのまま上流の値を下流に流す

乗算ノードは上流の値にひっくり返した値を返します

***
### 12. レイヤー
ノードをレイヤとして実装していきます。
次からはニューラルネットワークを構成する層(レイヤ)を1つのクラスで実装することにします。
レイヤは機能の単位です。シグモイド関数のためのSigmoidや
行列の積のためのAffineなど、レイヤ単位で実装を行います。
乗算レイヤの実装です。

例題


加算レイヤの実装

例題

#### 活性化関数レイヤの実装
##### ReLUレイヤ
数式では、

微分すると

微分すると、つまりBackwardのときは、(x>0)の場合で1をひょうじします
実装します。

Rekuはmaskという変数を持ちます。maskはTrue/FalseからなるNumpy配列です。
##### Sigmoidレイヤ
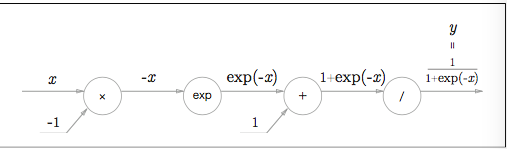
段階を追ってみていきます。
ステップ1

ステップ2

ステップ3

ステップ4

実装は簡単

#### Affine/Softmaxレイヤの実装
行列の要素数を一致させるために、ニューラルネットワークではAffineレイヤを実装します。(幾何学の分野ではアフィン変換と呼ばれます)
Affineレイヤの計算グラフは以下のようになります。

数式はこうです

Tは転置を表します。

列と行が変わります
Affineの逆伝搬は図で示すとこうなります
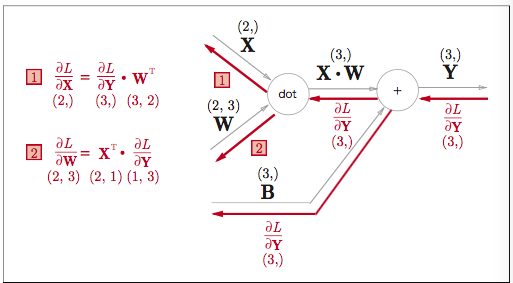
行列の形状に注意すると

WTで転置することが必要です。
#### バッチ版Affineレイヤ
バッチではN個のデータをまとめて順伝播する場合、図のようになります。
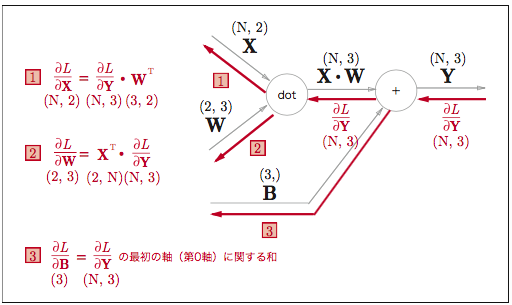
実装するとこうです

#### Softmax-with-Lossレイヤ
ソフトマックス関数は入力された値を正規化して出力します。
なお、ソフトマックスは推論では使用しません。なぜなら最大値に興味があるのでソフトマックスは必要ないです。
図で表すと、

入力画像が、Affine レイヤと ReLU レイヤによって変換され、Softmax レイヤによって 10 個の入力が正規化される。この例では、「0」であるスコアは 5.3 であり、これが Softmax レイヤに よって 0.008(0.8%)に変換される。また、「2」であるスコアは 10.1 であり、これは 0.991(99.1%) に変換される

Softmax レイヤは、入力である (a1,a2,a3) を正規化して、(y1, y2, y3) を出力します。
Cross Entropy Error レイヤは、Softmax の出 力 (y1, y2, y3) と、教師ラベルの (t1, t2, t3) を受け取り、それらのデータから損失 L を出力します。
注目すべきは、逆伝播の結果がy1-t1ときれいな形状ででていることです。この差分である誤差が前レイヤへ伝わっていくのがニューラルネットワークの学習における重要な性質です。
何度も言いますが、ニューラルネットワークの学習の目的は出力(ソフトマックスの出力)を教師ラベルに近づけることでした。その為、ニューラルネットワークの出力と教師ラベルとの誤差を効率よく、前レイヤに伝える必要があります。先程のy1-t1という結果は出力と教師ラベルの差であり、目的を果たしています。
実装してみます。

バッチの個数batch_sizeで割ることでデータ1個あたりの誤差が前レイヤへでんぱする点に注意
### 14. BACKPROP実装
#### 誤差逆伝搬法の実装
集大成です。
全体図としては、
前提:ニューラルネットワークは、適応可能なおもみとバイアスがあり、この重みとバイアスを訓練データに適応するように調整することを学習という。
1.ミニバッチ:訓練データの中からランダムに一部のデータを選び出す
2.各重みパラメータに関する損失関数の勾配を求める
3.パラメータの更新:重みパラメ0たを勾配方向に微小量だけ更新する
4.繰り返す


OrderedDictをいれることで逆伝搬でも逆の順番で呼び出すようになります。
### 勾配確認
数値微分は計算は遅いですが、実装は簡単です。
Backpropは計算が高速ですが、実装が複雑になるためミスが起きやすいのが一般的です。
そこで、数値微分の結果と誤差逆伝播法の結果を比較して、誤差逆伝播法の実装の正しさを確認します。これは勾配確認といいます。それでは勾配確認を実装します。

各重みパラメータの要素の差の絶対値を求め、平均を算出します。上のコードを実行すると、次のような結果が出力されます。
b1:9.70418809871e-13
W2:8.41139039497e-13
b2:1.1945999745e-10
W1:2.2232446644e-13
結果から、数値微分と誤差逆伝搬法で求めた勾配の差はかなり小さことがわかります。
### 誤差逆伝播法を使った学習
それでは最後に、学習を実装します。

まとめ
* ニューラルネットワークの構成要素をレイヤを実装することで勾配を効率的に求めることができる(誤差逆伝搬法)
* 数値と誤差逆伝播法の結果を比較することで実装に間違えないか確認できる(勾配確認)
### 学習に関するテクニック
この章で取り上げるのは
*最適な重みパラメータを探索する最適化手法
*重みパラメータの初期値
*ハイパーパラメータの設定方法です。
ニューラルネットワークの学習においてキーtなる重要なアイディアとなります。
また、過学習の対応策として、Weight decayやDropoutなどの正規化手法について概要と実装を説明。
最後に、多くの研究で使われるBatch Normalizationという手法について説明します。
これらを行うことで、学習が効率的に進み、認識精度が上がります。
まとめ
*パラメータの更新方法にはSGDの他に、有名なものとしてMomentumやAdaGrand,Adamなどの手法がある
*重みの初期値の与え方は正しい学習を行う上で非常に重要
*重みの初期値として、Xavierの初期値やHeの初期値などが有効
*BatchNormalizationを用いることで、学習を早く進めることができ、また、初期値に対してロバストになる
*過学習を抑制するための正規化の技術として、Weight decayやDropoutがある
*ハイパーパラメータの探索は、良い値が存在する範囲を徐々に絞りながら進めるのが効率が良い
***
## 実験
### 実験の概要
・レポートの構成要素8つに乗っとり進めます。
1. 目的:少ない学習回数で、誤差を小さくすること
(大枠:XORゲートを数値微分で学習した場合、どこを変更すると値がどれくらい変わるのかを知り、関数や各コードごとの繋がりを理解する→他のアルゴリズムでも同じプロセスを踏むことができるようになることを大きな目的とする)
2. 原理:XOR・損失関数・活性化関数・勾配法・数値微分
3. 装置および方法:Qiita/Jupyter
4. 結果:実行結果のグラフでの表示
5. 考察:関数や学習率を変更することで、学習回数を少なくかつ、入力と正解データの誤差が0に近づくと仮定。
6. 検討:1.活性化関数を変える、2.損失関数を変える、3.ランダムで重みを変えるが、ランダムの分布を変えてみる、4.学習率を変えてみる
7. 参考文献:ゼロから学ぶディープラーニング/Qiita等
8. 付録:省略した箇所・補足説明
### 今回の実験のベースとするもの
ベースとするのは、シンプルで簡単なXORゲートです。
[0,0],[1,0],[0,1],[1,1]を入力し、正解データ[0,1,1,0](XORゲート)になる確率が近づくようなとなるようなパーセプトロンを確率的勾配降下法で学習させる。
・学習回数は10000回
・損失関数は2乗和誤差
・活性関数はシグモイド関数
実装はこちら。
パーセプトロンの実装

実行

### 実験の具体的内容(目次)
1.活性化関数のbetaの値を変えて、グラフの滑らかさを変えると、どの値が一番誤差が縮まるか(0に近くなるか)
2.loss関数を二乗和誤差から、クロスエントロピー誤差に変更した場合の誤差の変化
3.重みのランダムに値を振る際の分布を一様分布と、正規分布にした場合の誤差の変化
4.学習率(learning_rate)を変えた場合の誤差の変化
#### 0.重みをランダムでふっているので、ランダムの値を固定するために10回実行した中で、一番いいモデルを選び、値を固定して、後の実験に使用する。
beta = 10の場合
ランダムで重みをふっているので、10回同じモデルを実行し、似ているパターンを出します。
パターン1

学習回数4000~5000回で誤差は限りなく0に近い値になっています。
パターン1が一番スムーズに学習をおこなえた場合になります。このパターンは10回中2回登場します。
パターン2


学習回数が5000~10000回の間で誤差が限りなく0に近づく。
このパターンは10回中2回でています。
パターン3

誤差の値が0.3で止まっている場合もありました。10回中1回確認しました。
パターン4


誤差の値が0.5で止まっている場合です。
このパターンが一番登場回数が多かったです。10回中5回確認しました。
以降の実験では、一番学習がうまくいった**パターン1**を使用して、どうしたら誤差を0に近づけていくかを試していきます。
#### 1.活性化関数のbetaの値を変えて、グラフの滑らかさを変えると、どの値が一番誤差が縮まるか(0に近くなるか)
beta=10で一番誤差が0に近いモデルを今回のベースとしています。
beta = 1の場合
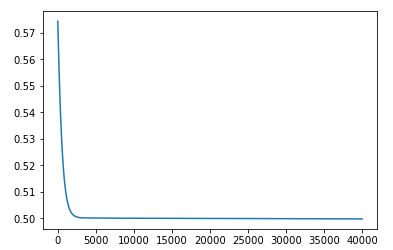
beta=1はシグモイド関数のデフォルト値です。
誤差の値は0.5で止まっています。もうすこし学習回数を増やすと0に近づくと思われます。
beta = 3 の場合
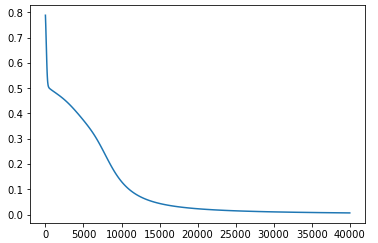
学習回数15000~20000回で、値は0に限りなく近づいています。
beta = 5の場合

beta=3よりも早い段階の学習回数10000~15000回で、値は0に限りなく近づいています。
beta = 7の場合
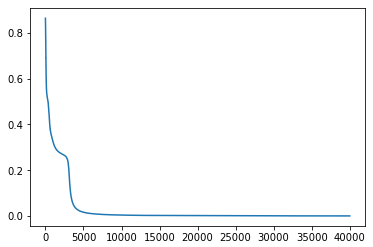
beta=5よりも早い段階の学習回数7000~10000回で、値は0に限りなく近づいています。
beta = 8の場合

グラフを目視しては差異がわからないので、拡大します。
範囲は
```py3:
plt.xlim([35000,40000])
plt.ylim([0, 0.001])
```としてます。
beta = 9の場合
グラフの形が

beta = 12の場合

beta=13~15までの場合も試しましたが、めぼしいものはなかったので省いています。
beta = 16の場合

学習回数35000〜400000の際、誤差の値は0.0002程で止まっています。
beta = 17の場合

映らなくなりましたので、一度全体像を見ます。

すると、誤差が0.25で止まっていました。

beta=20以後も0.25で止まっています。
試しに学習回数を増やしてグラフをみてみると(学習回数を通常の10倍の400000に指定)

学習回数が40000~50000回の際に、0に限りなく近づいています。
今回は「少ない学習回数で、誤差を小さくすること」を目標としているので、これ以上は追いません。
(beta=16で、誤差が0.25でとまっているのを見ると、4が関係ありそうで、数学の話が入ってきそうですが、ここでは省略します。)
今度は、学習回数がすくない段階で0.00002に近づいているモデルを探します。
beta=16の場合

学習回数が40000回以降で0.0002に近づいている。
beta=14の場合

学習回数が35000回で0.0002を超えている。
beta=12の場合

学習回数が40000回以降で0.0002に近づいている。
このなかで、beta=14が誤差が小さいことが分かり、近い値のbeta=13,15の場合を見る
beta=13の場合

学習回数38000回で0.0002を超えている。
beta=15の場合

学習回数35000回で誤差が0.0002をこえている。

結果、この場合beta=14が学習回数が少なく、誤差が一番小さいbetaの値となる。
#### 1のまとめ
betaを大きくするごとに誤差が小さくなっていきます。しかしbeta=17以降は0.25で一度誤差の減少が止まり、学習回数が50000回でまた減少を始め誤差が0に近づきます。
なぜ、beta=16以降で、誤差が0.25でとまるのかは調べましたが、今回は理由がわかりませんでした。今後、深く突き詰めてみたいと思います。
この場合、beta = 14の場合で、学習回数が少なく誤差を0に近づけることができることがわかりました。(betaは整数の場合)
#### 2.loss関数を二乗和誤差から、クロスエントロピー誤差に変更した場合の誤差の変化
デフォルト(二乗和誤差で損失関数のbeta=10の場合)だと、

で、学習回数が35000~40000回のとき、誤差の値は0.0002でした。
beta = 10のときに、クロスエントロピー誤差を使用する場合

グラフは緩やかに見えますが、y軸を見ると、誤差は0.0000065~0.0000025となっており、二乗和誤差よりクロスエントロピー誤差の方がよいということがわかります

表では学習回数40000回の時点で比較していますが、グラフを見ると分かるように5000回の時点でクロスエントロピー誤差は0.0000055(二乗和誤差の100分の1)ほどであり、クロスエントロピー誤差のほうが再生回数少なく、誤差も小さくなります。
#### 2のまとめ
二乗和誤差より、クロスエントロピー誤差の方が学習回数が少なく、誤差が小さい。今回の場合、クロスエントロピー誤差を使用したほうがいいと分かる。
#### 3.重みのランダムに値を振る際の分布を一様分布と、正規分布にした場合の誤差の変化
シグモイド関数のbeta=10のとき、二乗和誤差で、一様分布の場合
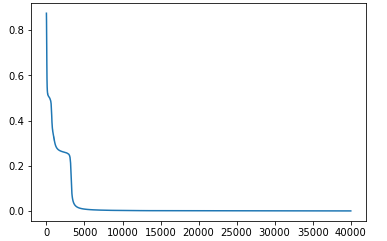
一様分布はnp.random.rand()で実装できる。今回の実験ではデフォルトで一様分布を使用している。
シグモイド関数のbeta=10のとき、二乗和誤差で、正規分布を見る場合
正規分布はnp.random.randn()で実装できる。

グラフは

拡大すると、

再生回数が0~400000回で、誤差は0.5で止まっている。
ちなみにbeta=14でクロスエントロピー誤差を使い、正規分布をみる場合

拡大すると

学習回数が35000〜40000のとき、誤差は0.00002。
一様分布でクロスエントロピーの場合

拡大すると、

y軸を見ると一桁小さい(0.1倍)ことがわかる。よってこの場合一様分布のほうが誤差が小さくなる。
まとめとして、学習回数が40000回のときの誤差を比較した表になります。

#### 3のまとめ
一様分布と正規分布を比較すると、一様分布の方が誤差が小さいため今回は一様分布を使用したほうがいいと分かった。
正規分布は学習回数を何回上げても0.5で誤差が止まってしまっている。詳しくは調べたがわからなかったので、正規分布等の統計の応用から損失関数や活性化関数の数式と関連させてなぜ0.5で止まっているのかを勉強する必要がある。
#### 4.学習率(learning_rate)を変えた場合の誤差の変化
今回はlearning rate = 0.01をデフォルトとしています。

a.learning rate=0.1の場合(10倍)

x軸を0~1000の範囲で拡大すると、

さらに、誤差を見るためy軸を0~0.02の範囲で拡大すると、

学習率が0.1の場合、学習回数が1000回のとき、誤差は0.0025です。
b.learning rate=0.001の場合(10分の1)

学習率を10分の1にした場合、学習回数が35000〜40000回で0に近づいているが、このグラフではわからないため、学習回数を2倍の20000に増やしてみると。

となり、40000~50000回学習したとき0に近づいている。
次からは学習率0.1の方が早く誤差を縮めることができるので、学習率を増やしてみる。
learning rate=1の場合(100倍)

x軸を0〜2000の間で拡大すると、

一度、0.5に近づいて1に戻っています。これは学習率が大きすぎて変な方向にいってしまっている可能性が高い。
d.learning rate=0.2の場合(20倍)

学習回数4000回ほどで誤差は0に近づいていますが、学習率0.1は学習回数が1000回で、誤差は0.0025でしたので、学習率0.2より学習率0.1の方がいいです。グラフ中の値が往復して太く見えている部分については調べてみましたが理由はわかりません。仮説として、シグモイド関数(1/(1 / np.exp(-x))のxに0.2を代入すると繰り返したときに、誤差の範囲が0.2の間を往復するのではないかと考えていますが、時間がかかるのでここでは省略します。
次は0.1から減らしてみていきます。
learning rate=0.09の場合(9倍)

x軸0〜2000、y軸0〜0.002の範囲で拡大すると

学習回数1000回のときに誤差は0.0025に達していない。つまり、学習率0.1の方がいいということがわかります。
learning rate=0.11の場合(11倍)
x軸0〜2000、y軸0〜0.002の範囲で拡大すると

学習率0.11のグラフですが、学習回数1000回のときに誤差は0.0025に達していない。つまり、学習率0.1の方がいいということがわかります。
結果、学習率は0.1が最も学習率が少なく、誤差が小さくなります。
ちなみに、今まで検証した結果、最適である値のlearning rate=0.1で、シグモイドのbeta=14,一様分布,クロスエントロピー誤差を使った場合

拡大すると、
学習回数40000回で、誤差が0.0000009~0.000001となっているので、とても正解に近い。
比較するために、学習率を編集する前の誤差は(learning rate=0.01で、シグモイドのbeta=14,一様分布,クロスエントロピー誤差を使った場合)は

学習回数40000回で、誤差は0.000006です。学習率0.1の場合、この0.1倍以上誤差が小さいので、学習率0.1にしたほうが誤差が縮まる。
表にすると
#### まとめ
学習率は0.1のとき、最も学習率が少なく誤差も小さくなる。
### 結論
損失関数はクロスエントロピー誤差を使用し、
活性化関数であるシグモイド関数の滑らかさを変化させる値(beta)を14とし、
分布は一様分布を使用し、
学習率が0.1の場合、学習回数が少なく、入力データと正解データの誤差の値は小さくなる。
### 最後に
勉強してみて、わかったことと次のアクションを最後に示します。
*理解の難易度が高いものほど、じっくりしっかり理解してから進める必要がある。高校までの暗記の勉強法は逆に非効率で学習スピードが落ちてしまうことが分かった。なので、今後はレポートにまとめるというアウトプットを目標に、インプットします。
*エンジニアをするのであれば、数学やロジックの理解を深めないければいけない。今まで、避けてきたが、どのみちどこかで当たる壁なので、時間のある大学時代に基礎となる数学とロジックの定着をさせる。
*中途半端な気持ちで勉強するのはなんのスキルもつかないので、結果的に時間がもったいなく、きつくても最後までやることが大事。隣の芝は青く見えるが、1つ1つ終わらせてから。
*ref
1.`astype`とは、ndarrayの要素のデータ型を別のデータ型にしたndarrayを生成します。元のndarrayとは別のadarrayが生成されるので、要素を変更しても元のndarrayには影響しません。
`ndarray`とはNumpyに元々はいてるやつ。詳細にいうと、配列(行列)を高速に扱うための ndarray クラスが用意されています。