概要
2019年に、AAAI-19に掲載された論文 "Unsupervised Domain Adaptation by Matching Distributions Based on the Maximum Mean Discrepancy via Unilateral Transformations"の紹介です。
ドメインアダプテーション(DA)とは?
識別器を学習する際には、実際に識別器が扱うデータ(=ターゲットデータ)を使って学習することが一般的だと思います。しかし、ターゲット環境に例えば次のような制約
- データを持ち出せない
- データ件数が少なく、学習に足るほど十分でない
があったりして、現実的には学習データ(=ソースデータ)とターゲットデータが異なるケースも多いと思います。
そうすると、ソースデータでは上手くいったが、ターゲット環境では識別性能が十分でない、ということが発生します。
DAとは、ソースデータとターゲットデータに差があっても、学習によって獲得した識別性能をターゲットデータに対しても発揮できる手法です。
DAには様々な種類がありますが、本論文の問題設定は次の通りです。
- ソースデータにはラベルがあるが、ターゲットデータにはラベルなし
- ソースデータとターゲットデータでは、同じカテゴリ数とする
論文での解決手法
手法の概略
- 何か別の手段(DNNなど)を用いて、ソースデータとターゲットデータの特徴量を計算する
- ソースデータの特徴量(FeatureS)からターゲットデータの特徴量(FeatureT)へ変換する変換Fを学習する(後述)
- 変換Fを使い、変換後のFeatureSとソースデータのラベルを使って、変換Gを学習する
- 変換Gを使ってターゲットデータの特徴量を分類する
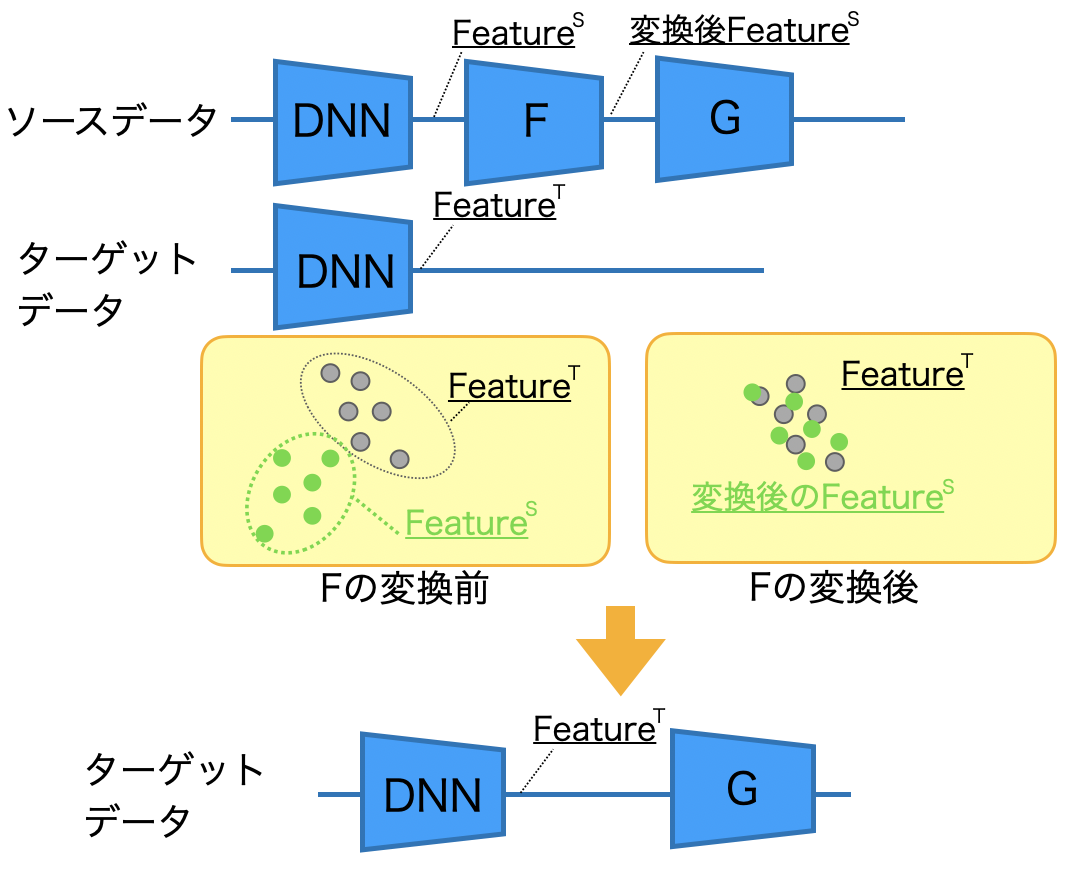
変換Fの求め方
ソースデータとターゲットデータを正定値カーネルを使って特徴空間に写像し、写像した特徴ベクトルの平均(カーネル平均)を使って評価します。論文中の式を示します。
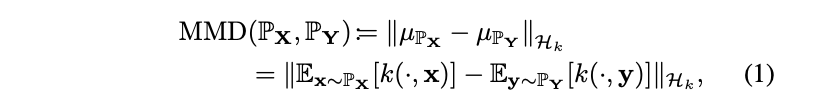
MMDとは、特徴空間に写像された2つの分布(PX, PY)をノンパラメトリックに評価する手法です(論文の原文を参照)。
The maximum mean discrepancy (MMD) (Gretton et
al. 2012) is an effective non-parametric criterion that compares the two distributions by embedding each distribution
into the RKHS.
PX=PYの時、MMDは0となります。EX〜PX[k(・,X)]は、元データXの分布の全てのモーメント(平均、分散、尖度、…)を保持するという便利な特性があり、元空間での分布を評価するより精度良く評価できます。
この特性を直感的に説明します。
カーネル関数をTaylor展開します。
$$
k(u,x)=c_0+c_1ux+c_2(ux)^2+\cdots
$$
カーネル関数の期待値をとると、平均、分散などモーメントが含まれていることが分かります。
$$
E[k(u,x)]=c_0+c_1E[x]u+c_2E[x^2]u^2+\cdots
$$
このMMDを使って目的関数L(A)を定義して、評価します。
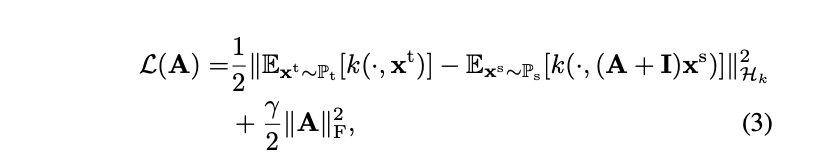
第1項はMMDで、第2項は正則化項です。Xtはターゲットデータの特徴量、Xsはソースデータの特徴量、変換F(=A+I)で変換したソースデータの特徴量がターゲットデータの特徴量に近づくように学習します。
実験
2つの異なるタスクで実験しています。1つはクロスドメインの物体認識のタスク(Office-Caltech10)で、1つはクロスドメインのレビューの感情分析(Amazon-Review)のタスクです。
学習データは少なく、Office-Caltech10では1クラスあたり20サンプルで10クラスのデータを学習に使用しており、Amazon-Reviewでは1600件を使用しています。
実験結果をTable1に示します。Proposedが本論文の方式、NoAdaptは変換せずソースデータの特徴量のままSVMを学習したもの、他に4つの代表的な方式と比較しています。
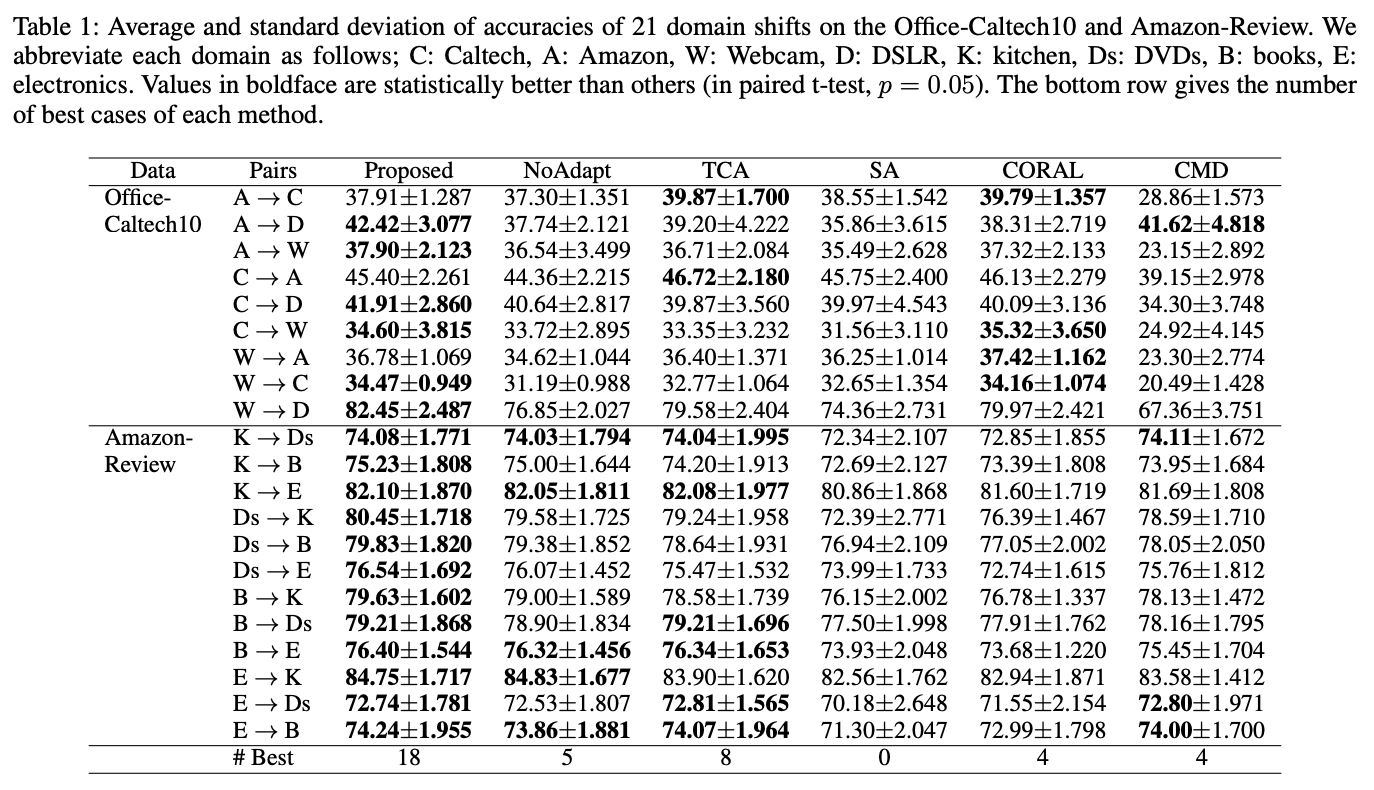
正解率の高さが統計的に有意な結果は太字で示しており、そのよい正解率の数を最後の#Best行に示しています。この数を見ると、本論文の方式は他の方式より良い結果であることを示しています。
まとめ
少ないデータで教師なしドメインアダプテーションを精度良くできたことが分かりました。
論文には、ImageNetでpretrainしたネットワークを使う方式と比べると、学習に必要なデータ数が少なくて済むため、収集するデータが少ないタスク(bioinformaticsや医療関連など)で有益な方法であると書いてありました。大量データがある場合には、また別の方法がよいかもしれないです。
カーネルの勉強が難しかったです。