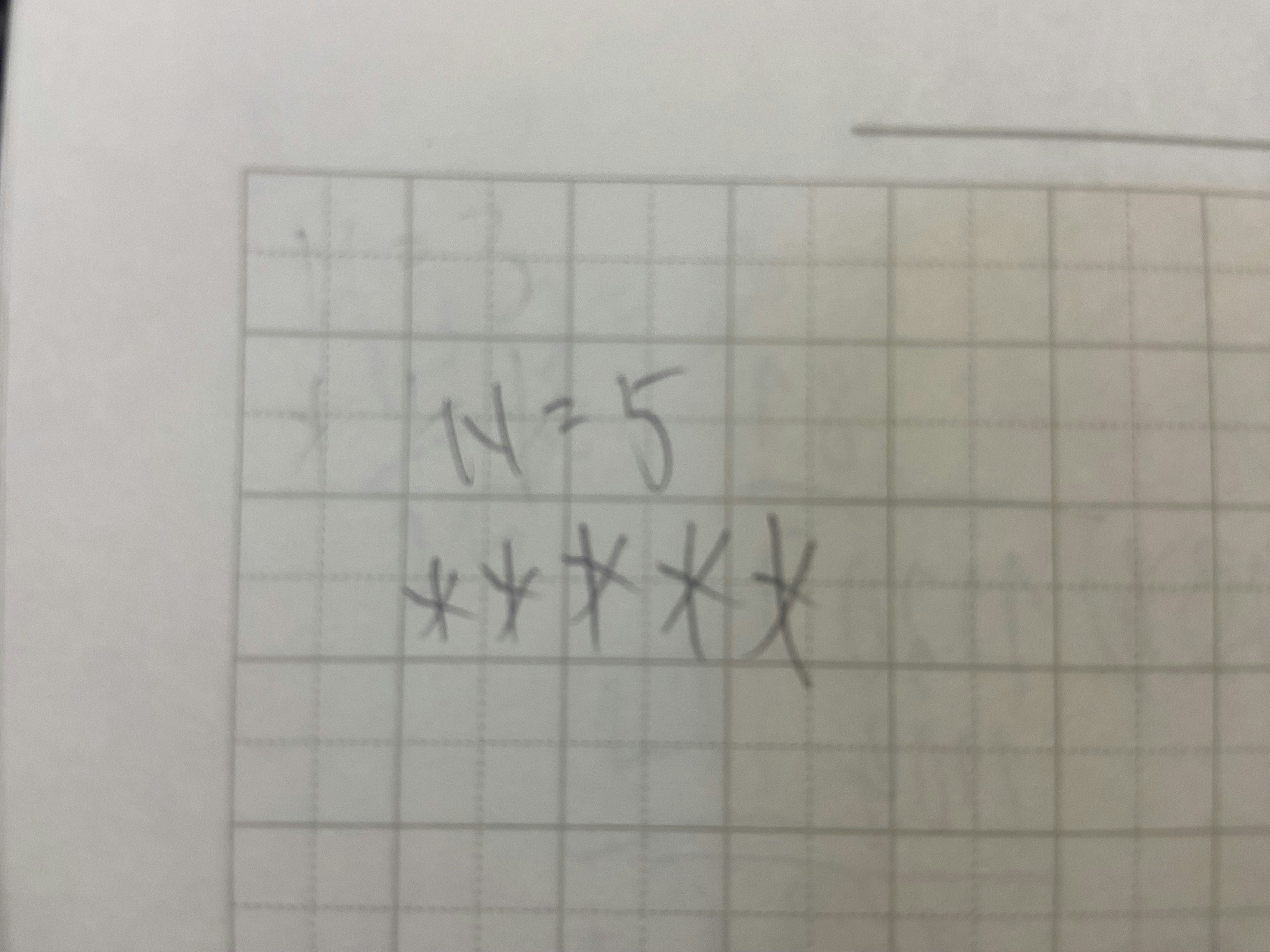paiza×Qiitaコラボ 第1弾 D~Sランク問題に挑戦

• 経緯
  自分もQiitaで記事を書いてみたいなと思っていたところ, 誰でも参加できるこのキャンペーンを見つけたので主にPythonで挑戦してみました！

  この記事では問題を解く際にどのようなことを考えたかを伝えたいと思います。

  Sランクが解けなかったのは悔しいですが, 自分もこういうキャンペーンに参加できるんだという実感が得られたので, 参加して良かったなと思います。

  paiza×Qiitaコラボキャンペーン第2弾の方は8/29(木)までやっているようなので, ちょっと気になるなと思ったら皆さんも気軽に参加してみてください。

D007:N倍の文字列(正答)

• 問題の要約
  N個の*を横並びで表示せよ。

N = int(input())
print("*"*N)

C020:残り物の量(正答)

• 問題の要約
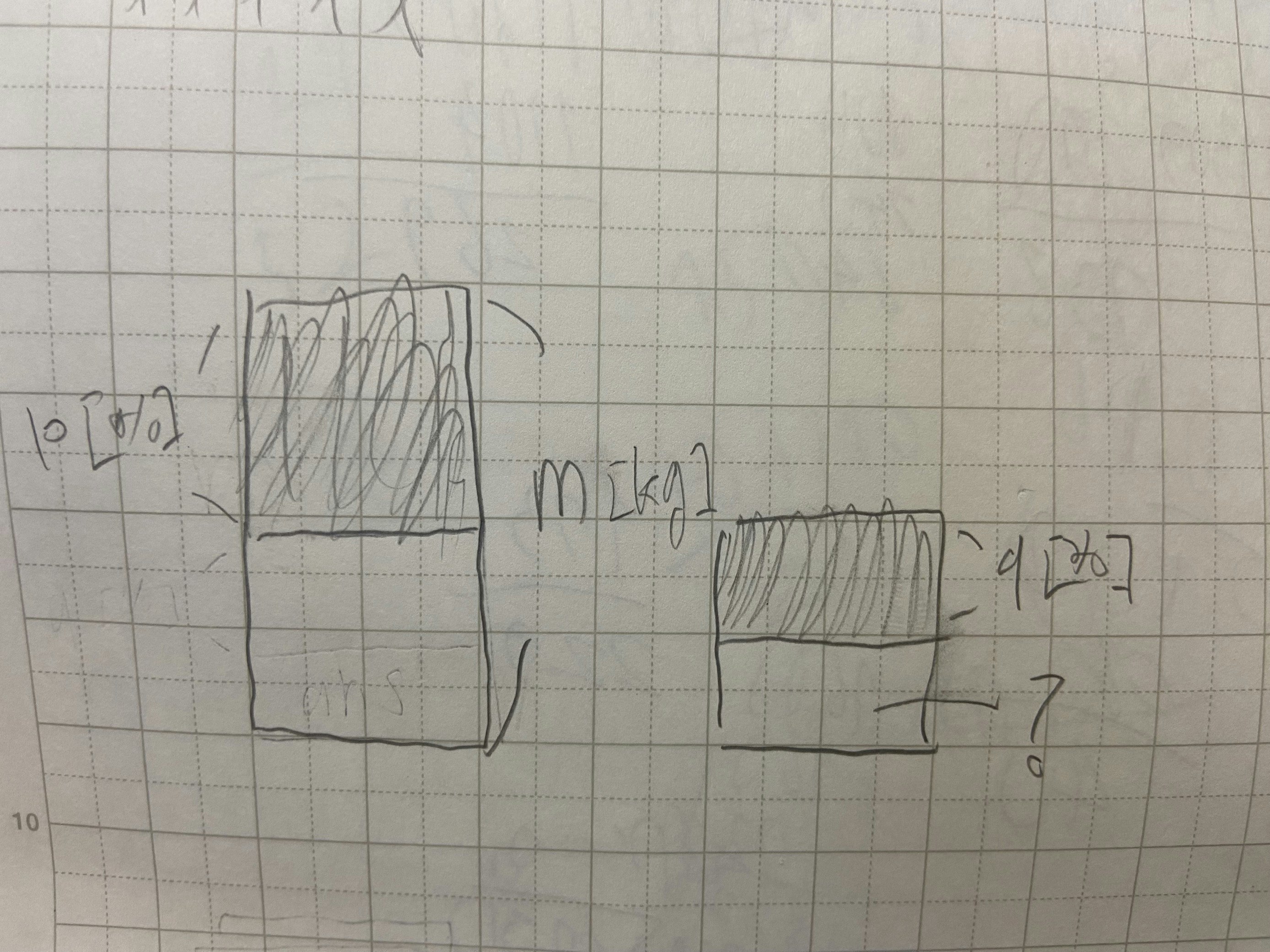
  m[kg]仕入れてp[%]が売れた。

  さらに残った分のq[%]が売れたとき, 最終的に売れ残ったのは何kgか。
  
  

• 考えたこと
  まず, 最初に売れたm[kg]のp[%]を求める。(mp)

  次に, 残った分(m-mp)[kg]のq[%]を求める。(mq)

  仕入れた分から先の2つを引けば最終的に売れ残った分が求まる。(m-mp-mq)

m, p, q = map(int, input().split())

mp = m*p/100
mq = (m-mp)*q/100

print(m-mp-mq)

B011:名刺バインダー管理(正答)

• 問題の要約
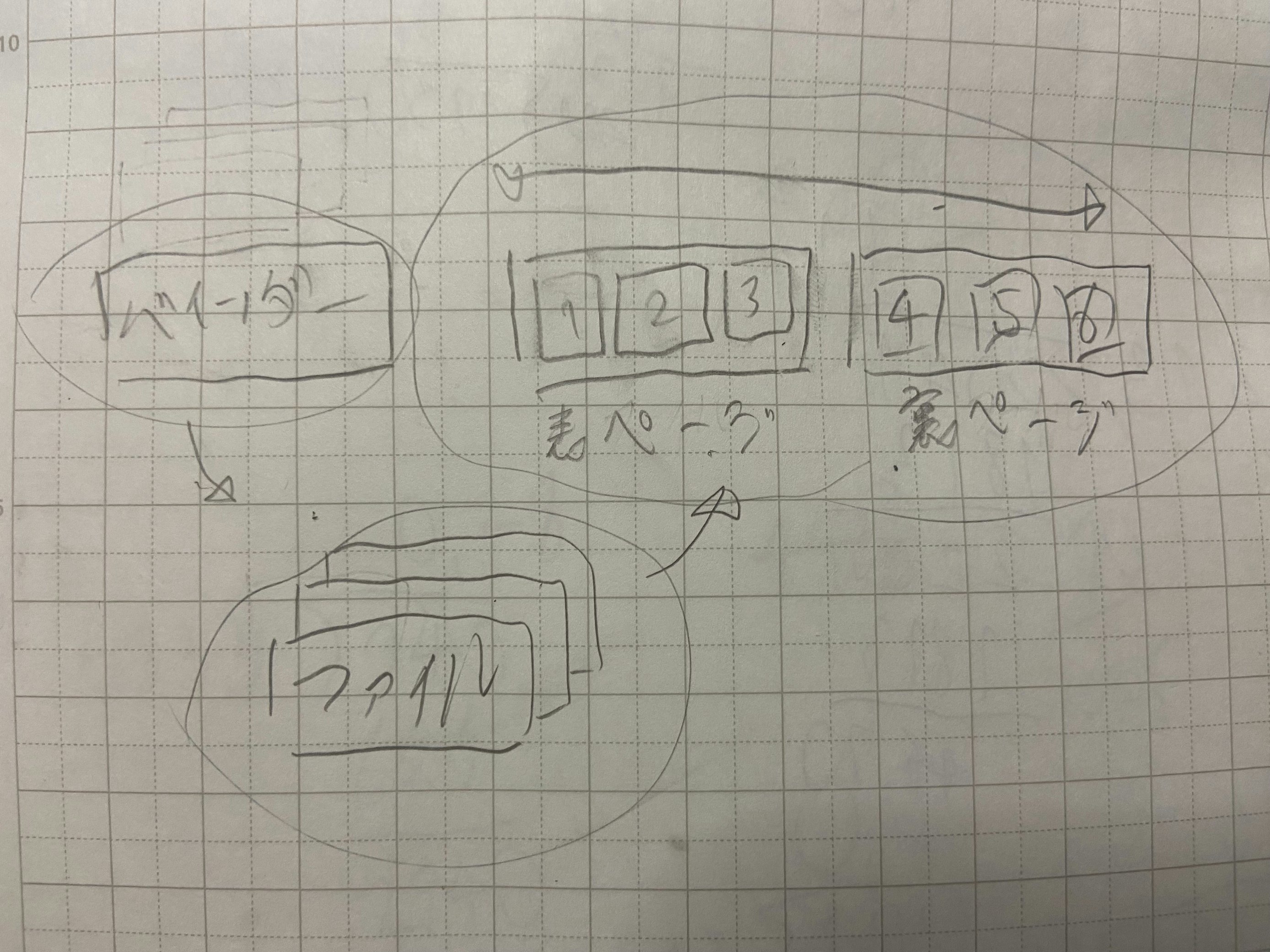
  バインダーには十分な数のファイルがある。

  ファイルにはn個のポケットがある。

  ポケットに左から名刺を詰める, めくって左から名刺を詰める, 次のポケットへ, ... を繰り返す。

  このときm番目に詰めた名刺の裏側には何番目の名刺があるか？
  
  

• 考えたこと
  ファイルは表と裏の2ページからなるとして, m番目の名刺が何ページ目にあるかを求める。(page)

  そうすると, ページの番号が偶数であれば表, そうでなければ裏だと分かる。(is_front)

  次に, ページ内で何番目のポケットにあるかを求める。(idx)

  最後に, m番目の名刺が表に存在するなら番号をプラスし, 裏に存在するなら番号をマイナスする。(ans)

N, M = map(int, input().split())
M -= 1

page = M//N
is_front = page%2 == 0
idx = M-N*page

ans = -1
if is_front:
    ans = M+(N-idx-1)*2+1
else:
    ans = M-idx*2-1
ans += 1
print(ans)

A034:お菓子の詰め合わせ(正答)

• 問題の要約
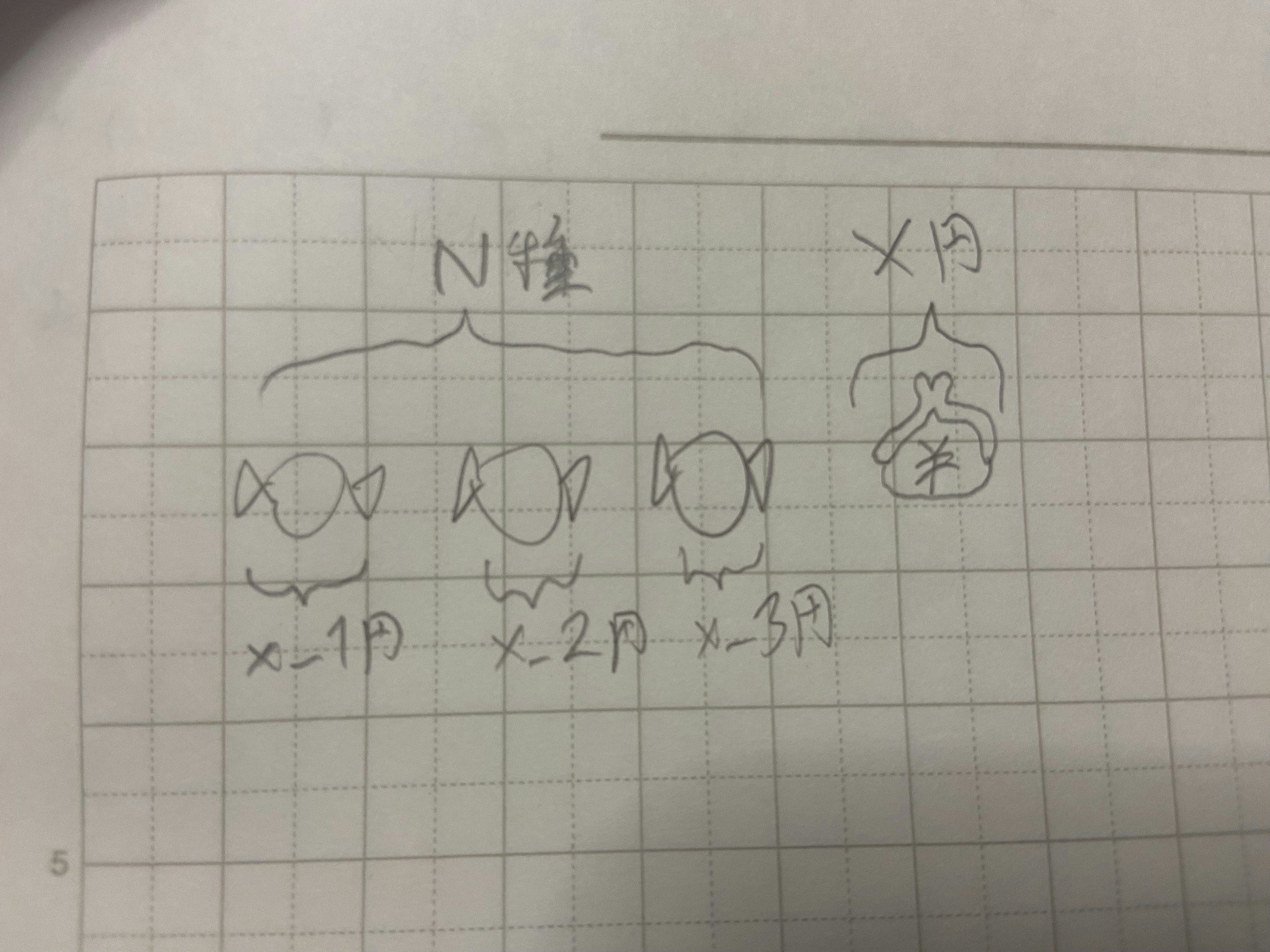
  N種類のお菓子が1つずつ売っており, 手持ちはX円。

  お菓子はそれぞれx_1[円], x_2[円], ...。

  なるべくたくさんお菓子を買うとき, お釣りは最小でいくらか。
  
  

• 考えたこと
  お菓子を値段の昇順にソートする。(A)

  安い方からお菓子を買って, 買える限界の数を求める。(kind_cnt)

  N <= 20なので, とりうるお菓子の組合せは最大でも2^20程度。

  とりうるお菓子の組合せを買うお菓子のビットを立てたビット列で表現することで全て網羅する。(bit全探索)

  買った数がkind_cnt以上かつ予算オーバーしていなければ, それまでの購入金額の最大値と比較し, 大きい方で更新する。(price_sum)

  手持ちから条件を満たす最大の購入金額を引けばそれが答えになる。(X-price_sum)

N, X = map(int, input().split())
A = list(map(int, (input() for _ in range(N))))

A.sort()

kind_cnt = 0
now_price_sum = 0
for ai in A:
    if now_price_sum+ai <= X:
        kind_cnt += 1
        now_price_sum += ai
    else:
        break
# print(kind_cnt)

price_sum = 0
masks = tuple(enumerate((1<<i for i in range(N))))
for bit in range(1<<N):
    now_kind_cnt = 0
    now_price_sum = 0
    for idx, mask in masks:
        if bit&mask > 0:
            now_kind_cnt += 1
            now_price_sum += A[idx]
    if now_kind_cnt >= kind_cnt and now_price_sum <= X:
        price_sum = max(price_sum, now_price_sum)

print(X-price_sum)

S023:村人の友好関係(誤答)

格闘しましたが解けませんでした！(供養)

• 問題の要約
  N人の村人とM個の友好関係がある。

  村人a_iと村人b_iの間には友好度f_iの友好関係がある。

  また, 同好会の人数は最初0人であり, 同好会への参加か脱退を表すQ個のログop_iがある。

  このとき, それぞれのログの時点における同好会の人気度を求めよ。

  なお, 同好会の人気度はグループ内の村人とグループ外の村人の友好度の最大値とする。
  
  

• 考えたこと
  計算量の関係上, paizaでsetが使いたいのでC++で書く。

  村人を頂点, 有効度を辺としてグラフを隣接リストで表現する。(G)

  ログが同好会への参加であればグループの頂点(g_node)に追加し, 追加した頂点からの辺をたどる。

  到達できる頂点がグループ内に存在するなら同好会の人気度の候補(g_cost)からコストを消去し, 存在しないなら追加する。

  同好会からの脱退であれば逆のことをする。

  ログごとに同好会の人気度の候補から最大値を求める。

#include <bits/stdc++.h>
using namespace std;

// typedef int int
typedef long long lng;
typedef double dbl;
// typedef char char
typedef string str;
// typedef bool bool

template<typename T>
using v = vector<T>;
template<typename T>
using vv = v<v<T>>;
template<typename T>
using vvv = v<vv<T>>;
template<typename T>
using vvvv = v<vvv<T>>;
template<typename T>
using vvvvv = v<vvvv<T>>;
template<typename T>
using vvvvvv = v<vvvvv<T>>;
template<typename T>
using vvvvvvv = v<vvvvvv<T>>;

template<typename T>
using uset = unordered_set<T>;
template<typename T, typename U>
using umap = unordered_map<T, U>;
// template<typename T>
// using set = set<T>;
// template<typename T, typename U>
// using map = map<T, U>;

template<typename T>
using deq = deque<T>;
template<typename T>
using prq = priority_queue<T>;

//--------------------

lng N;
lng M;
lng Q;

lng a;
lng b;
lng f;
map<lng, v<tuple<lng, lng>>> G;

set<lng> g_node;
set<lng> g_cost;
str op;
lng q;

int main(void) {
    cin >> N;
    cin >> M;
    cin >> Q;
    
    for (int i = 0; i < M; i++) {
        cin >> a;
        cin >> b;
        cin >> f;
        a--;
        b--;
        G[a].push_back(make_tuple(f, b));
        G[b].push_back(make_tuple(f, a));
    }
    
    for (int i = 0; i < Q; i++) {
        cin >> op;
        cin >> q;
        q--;
        
        if (op == "+") {
            g_node.insert(q);
            for (auto [f, to] : G[q]) {
                if (g_node.count(to)) {
                    g_cost.erase(f);
                } else {
                    g_cost.insert(f);
                }
            }
        }
        
        if (op == "-") {
            g_node.erase(q);
            for (auto [f, to] : G[q]) {
                if (g_node.count(to)) {
                    g_cost.insert(f);
                } else {
                    g_cost.erase(f);
                }
            }
        }
        
        cout << *max_element(g_cost.begin(), g_cost.end()) << endl;
    }
}