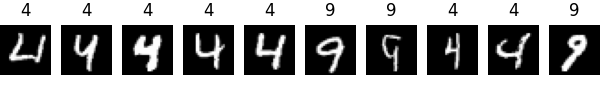前回の記事の続きです。
その1:金子勇さんのED法を実装してMNISTを学習させてみた
その2:ここ
その3:ED法+交差エントロピーをTF/Torchで実装してみた(おまけでBitNet×ED法を検証)
今回はED法を少し補足した後に性能について見てみました。
(ついでにNumPyで実装して高速化)
コード全体(Google Colaboratory)
今回実装したコードは以下に置いています。
パブリックドメイン相当で公開しているので自由に使ってください。
ED法(誤差拡散学習法)の実装について補足
前回で誤差を拡散するあたりの説明が弱かったので、具体的な数字を入れて補足しておきます。
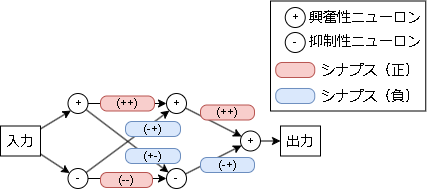
以下のような興奮性ニューロン3つ、抑制性ニューロン2つのモデルを考えます。
(元はシナプスも興奮性と抑制性に分けていますが実装上はまとめても問題ないので省略しています)
シナプスの符号は接続前後が同じ種類の場合"正"になり、違う種類の場合"負"になります。
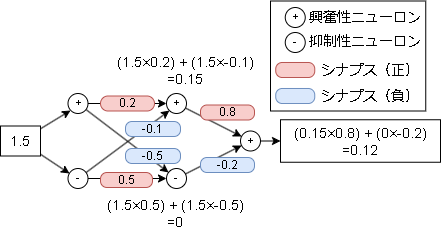
具体的に数字を入れると以下です。
シナプスに書かれている数字は強さです。(プログラム的には重み;Weightとなります)
このモデルは1.5の入力に対して0.12を返す計算になります。
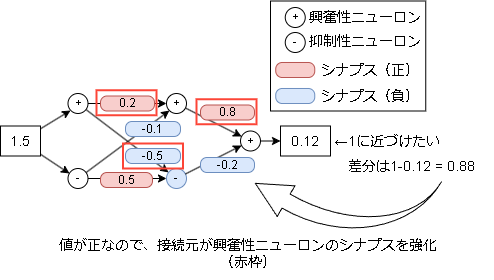
次にこの出力を1に近づけたい場合を考えます。
接続元が興奮性ニューロンのシナプスを強化します。
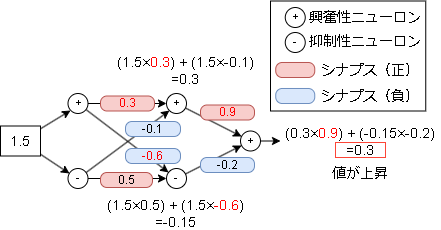
今回は仮に0.1増やしてみます。
出力の値が大きくなっていることが確認できます。
各シナプスをいくら増やすかは前記事の学習則の箇所になります。
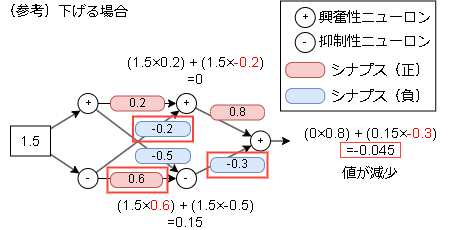
参考までに下げたい場合は以下で、接続元が抑制性ニューロンのシナプスを強化します。
たったこれだけの操作で学習するのがED法となります。
また、他の観点から考察してくれた方がいたので紹介しておきます。
集合知すごい…
生理学的な補足
実際の脳の動きにかなり近いようです。
今回接続元が興奮性ニューロンのシナプスを強化する形を取っていますが、金子さんはこれを実際の神経系ではないと記載していました。
実際は接続元・先で同じ種類のシナプスを強化する形らしいのでそこら辺がどうなっているかは気になりますね。
(ただこれだと"逆"と言われる現象が発生するらしくそこら辺の解釈も気になります)
数式的な補足
欠けていた学習則の部分まで書かれています。
なんで前の層の出力が掛けられているか謎でしたが数学的な理由があったんですね。
後これMSE(2乗誤差の最小化)による学習だったのか…(動けばいいの精神、よく見ればアーカイブに書いてあった)
交差エントロピーの最小化(クラス分類)や対数尤度の最大化(最尤推定)等でどうなるかが分かれば適用範囲が広がっていきますね。
また、sigmoid以外でもどうなるかが分かるようになるのかな?
他の方の実装
別の実装者も現れました。
しっかり数式から説明していてすごい…。
実装時の細かいポイント
・ミニバッチ学習
ミニバッチでは最終的な重みへの更新幅を合計してバッチ処理としています。
平均でもいいかもしれませんが、現状の実装だと更新に関係ない重みまで平均に数えられるのでうまくいかなくなり、試していません。
・重みの初期値
拡散の性質上、重みの初期値が大きいとUnit数の大きさに比例してforward時の合計が大きくなります。
それだとsigmoidですぐoverflowを起こすので重みの初期値は0~Unit数で割った値の範囲に抑えています。
・重みの学習
同じく拡散の性質上、全ての重みは同時に更新されます。
この更新幅ですが、元の数式にはUnit数は考慮されていなそうで、Unit数が増えるほど大幅に更新される現象が起きました。(こちらもsigmoidですぐoverflowになる原因だったり)
この更新幅をUnit数に依存しないようにUnit数+Layer数で割って、その値を更新幅としています。
検証
データセットですが、学習難易度を上げるためにMNISTの4と9の学習に変更しました。(0と1は簡単すぎて比較結果が見づらかった)
4と9はかなり似ており学習が難しい数字となります。
また、BP側の比較・参考用としてはKeras3を採用し、レイヤー・ユニット数・活性化関数を同じ条件で学習させています。
検証の全体は冒頭でも書いたGoogle Colabに置いてありますので、コードまで確認したい場合はこちらをどうぞ。
とりあえずの実行結果
動作確認も兼ねたベースラインっぽいものになります。
レイヤー数:3
ユニット数:16
バッチサイズ:64
学習率:0.01
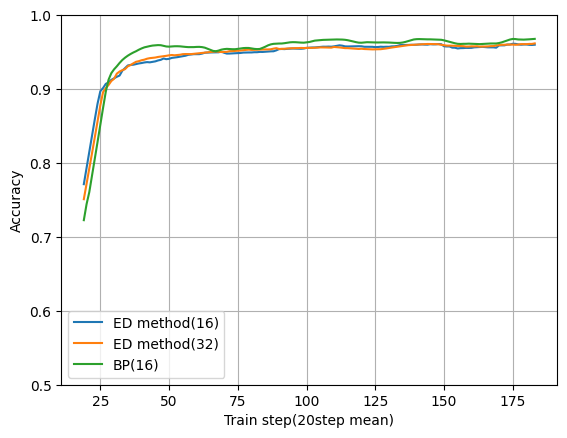
縦がValidation用データの正解率(学習データは含まれていません)、横が学習回数です。
学習回数は、例えばバッチサイズが64の場合は64データをまとめて1回学習させた回数となります。
図を見るとBPとほぼ同じ性能で学習できていますね。
ED method(32)はユニット数を32にしたものです。
ニューロンが2種類に増えているので倍にしないとBPと同じ条件にならないかな?と思って見てみましたがあまり変わりませんでした。
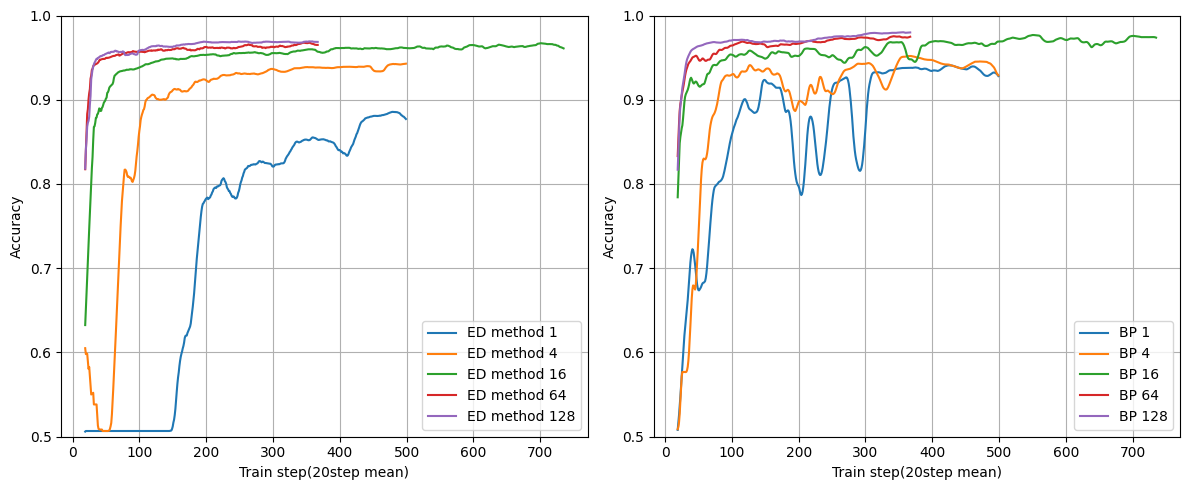
複数ユニット
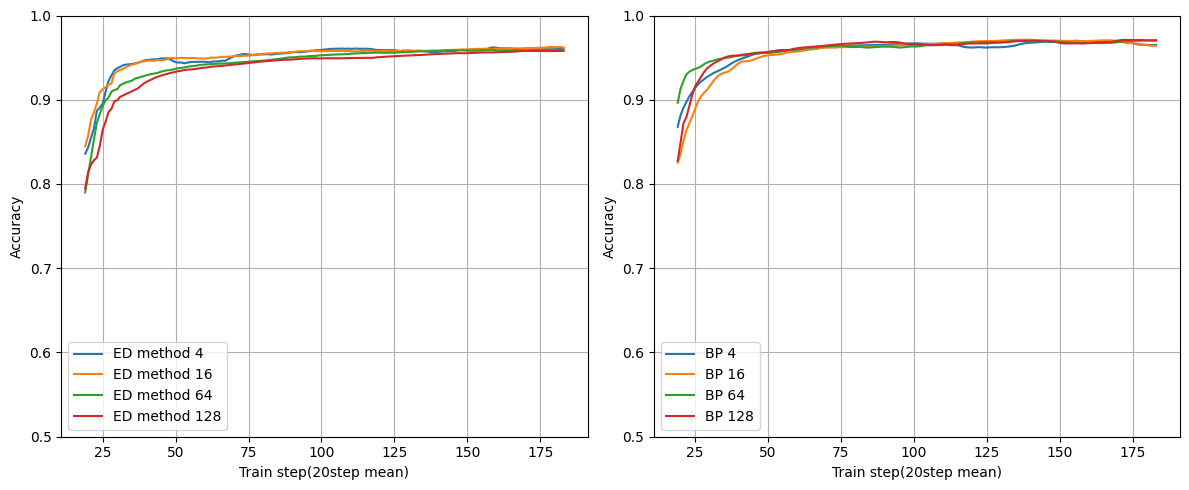
レイヤー数を固定にしてユニット数を変えた場合です。
まとめたら見づらかったのでBPの結果とED法の結果を分けています。
レイヤー数:1
ユニット数が増えてもちゃんと学習できそうです。
このレベルの学習だとユニット数はほぼ関係なさそうですね。
ただユニット数に比例して正解率が増えないのが気になりました。
金子さんは「EDは中間層ユニット数が増えるほど収束が早くなります」と言っているのでもしかしたら過学習を起こしているかもしれません。
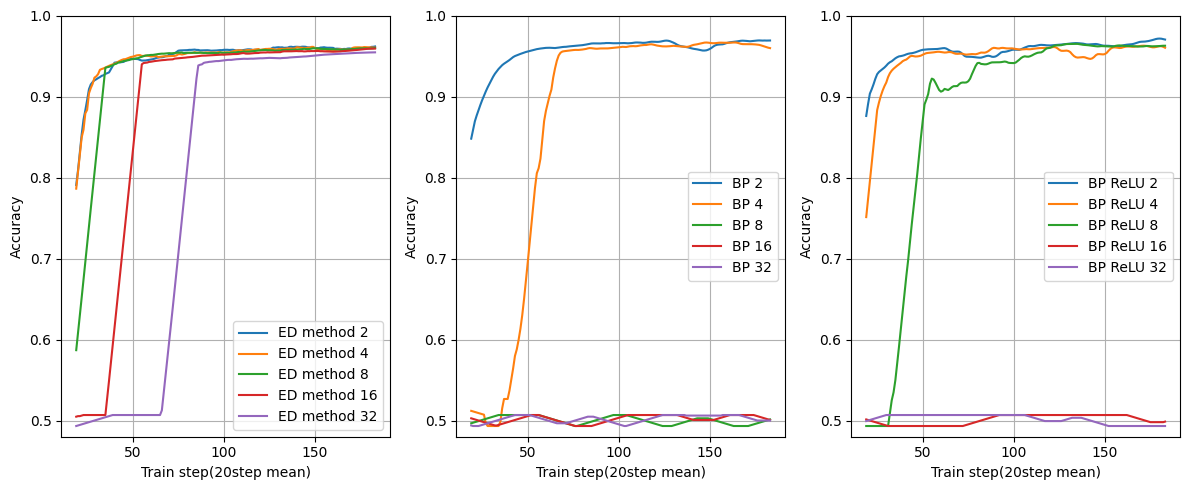
複数レイヤー
今度は逆にユニット数を固定にしてレイヤー数を変えた場合です。
BPはsigmoidだけではなく中間層をReLUにした場合も見てみました。
ユニット数:4
面白い結果になりました。
ED法はレイヤー数に関係なく学習できています。
BPは8層ですでに学習が出来ていませんね。これは勾配消失が起きているからです。
ReLUでは勾配消失を緩和していますが、それでも16層で学習できていません。
レイヤーを重ねても学習できるのはED法ならではのメリットになりそうです。
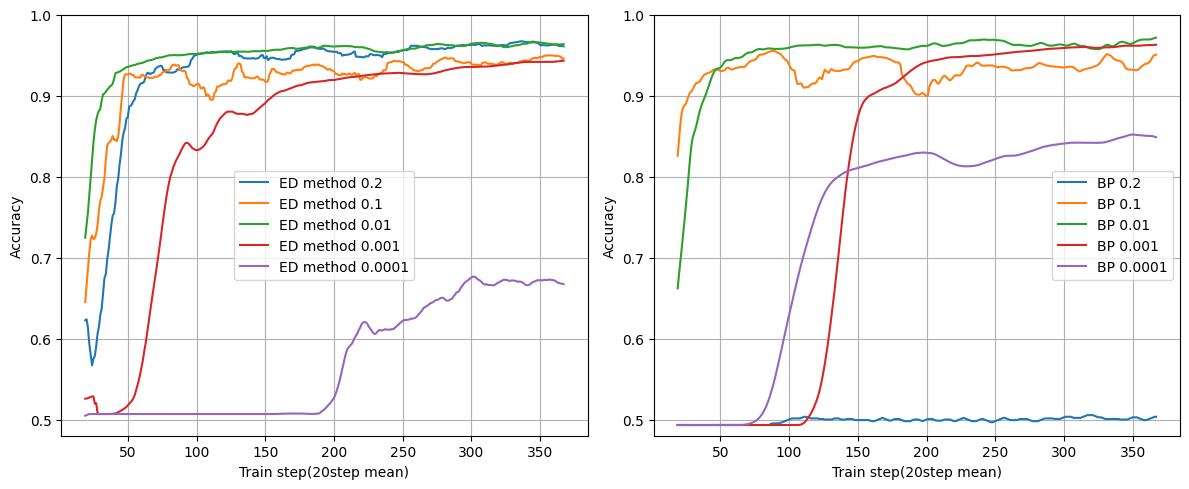
学習率
BPはAdamで学習しているのでED法とは学習率の意味合いが異なる点は注意してください。
学習のイメージを金子さんのアーカイブから引用すると以下です。
結局ED法は、階層型神経網学習における単純山登り法です。
BPも同様に山登り法ですが、BPがエラー関数の勾配による最急降下法であるのに対して、ED法は方向だけ考慮した特殊な山登り法です。
概念的にはパーセプトロンに近いです。BPが勾配情報で誤差を局所最小化するのに対して、ED法では回路構成を工夫することにより、階層型神経網でも確実に誤差が降下する方向に重みを変えます。
ただし、神経素子はEDでも、BP同様、シグモイド関数を用いるアナログ非線型素子です。
要約すると、BPは関数の勾配で学習方向を決めるのに対し、ED法はモデルの工夫で方向が分かった状態から学習、という感じです。
レイヤー数:2
ユニット数:16
バッチサイズ:32
学習率が0.2の場合にBPは学習ができていません。これは最急降下法の特徴で最適解を飛び越えて収束できていない状況です。
ただED法にはその傾向は見られません。
(多分PとNが上手い感じに最適解を飛び越えないように学習している?適当な考察)
(BPではバッチサイズがこの発散を回避する効果があり、バッチサイズを64にすると0.2でもBPは学習できるようになります)
大きい学習率でも学習できるのはED法ならではのメリットになりそうです。
ミニバッチ
大量のデータを学習したい場合どうしても必要になるので実装しました。
手法としてもプログラム的にもちゃんと学習できるのか確認する意味もあります。
バッチ数によっては学習に時間がかかりすぎるので学習回数はバッチサイズ毎に変えています。
レイヤー数:2
ユニット数:16
問題なく学習できていますね。
学習傾向もED法とBPであまり変わらなそうです。
速度
Keras(Tensorflow)との比較ですが、さすがに歴史が違うので参考程度になります。
これは手法の違いというより実装の違いによる影響がほとんどを占めます…
まずは前回のListとの比較です。
List time : 30.33958s
NumPy time : 0.83157s
numpy化で約36倍ほど早くなりました。
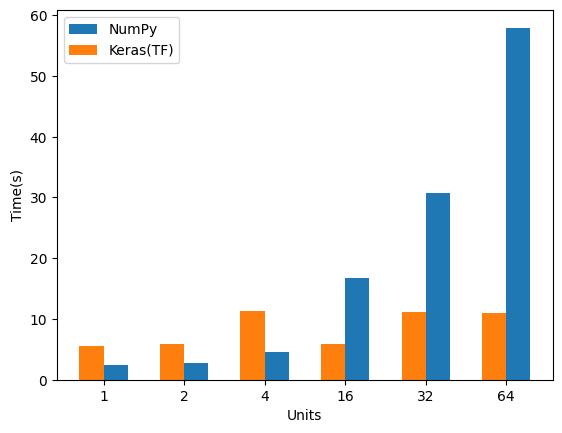
ユニット数
ユニット数のみを変えた場合です。
レイヤー数 :1
バッチサイズ:8
ユニット数に比例して時間が増えていきます。
というかTensorflowの時間がほぼ変わらないのはなんでだろ?どんな実装しているんだ…。
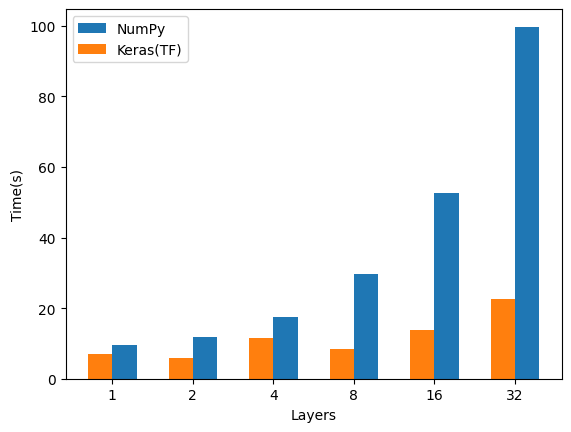
レイヤー数
レイヤー数のみを変えた場合です。
ユニット数 :8
バッチサイズ:8
ユニット数と変わらずですね。
自分でQ&A
-
Q、興奮性ニューロンと抑制性ニューロンは対になる必要はある?
A、多分ない気がします。ランダムに配置したほうが汎化性能が上がる気がしています(未検証)
また層の間の接続も全て接続するのではなくランダムに接続したほうが汎化性能が上がりそうです(未検証) -
Q、シナプスの強化(重みの上昇)を続けていたら値が無限に増えない?
A、増えそうですがなぜか増えません、多分sigmoidだから? -
Q、結果を下げる場合に興奮性ニューロン側のシナプスを下げるのではダメなの?
A、下げても学習できました。ただ抑制性ニューロン側を上げたほうが学習が早いような気がします。
多分ですが、これは出力に対して違う計算過程を経ているのでそこで汎化性能が高くなっているのかな?と思っていたり(未検証) -
Q、重みの初期値について0~1ではなく-1~1ではだめ?
A、いいような気はします。-1~1でも学習はできました。 -
Q、重み学習時の更新幅をUnit数+Layer数で割ってるけどUnit数*Layer数では?
A、最初はそう思って実装しましたがそれだと更新幅が小さすぎて学習できませんでした。
ここは数学的な数値が求められますが特にやっていません(動けばいい精神) -
不均衡データに関して
ED法の弱点として不均衡データに弱い気がしています。(未検証)
ただ、ここら辺は改善手法が割と簡単に発見されそうな気もしています。 -
ライセンスに関して
プログラム自体はUnlicenseとして公開します。
20年前なら公開方法はもう少し考える必要があったかもしれませんが、今の時代だとED法はもう少し研究が進まないと厳しいものがあると思っています。
(BPが培ってきた技術が多すぎる)
全体公開にしてED法の発展に貢献できればと思います。
ただ、ライセンスに関しての知識は弱いので公開方法に間違いや問題などあれば連絡お願いします。
まとめ
金子さんのまとめが(当然ですが)すごく的確だったので引用しておきます。
まとめ&考察
ED法は、実際の神経系の学習則として考え出された、階層型神経回路網の教師あり学習アルゴリズムです。
アミン系と興奮性・抑制性の効果を新たに考慮しており、特に中間層素子数が大きな場合に、優れた収束性を持ちます。
汎化能力は中間層素子数が少ない場合BPに劣りますが、中間層素子数が多い場合BPと同等です。
論理回路の学習に関しては、BPよりも優れています。
何よりも、BP法よりシンプルで動作が安定しているアルゴリズムであり、実際の神経系でも利用可能であると仮定できる点が重要です。
今回の結果だけでは断言できませんが汎化能力はBPと同等と言ってもいい気はします。
動作が安定しているという点は同意ですね、学習率の結果と同じ結論になっていると思います。
勾配消失が起こらない点、学習が安定している点あたりがBPより優れている点でしょうか。
強化学習についての考察
折角なので強化学習についても触れておきます。(フレームワーク作っていますし)
金子さんはこの学習を脳では強化学習に用いられているのではないかと予想しています。
さて、このEDが実際に脳内のどこで使われているのか?ですが、アミン系で特に学習との関連が深い部位でもっともありうると思われます。
ということは、報酬系と密接な関係を持つ前頭前野が最大の候補でしょう。
ここは動作のプランニングを行うところですが、ドーパミン駆動系(A9やA10)などを介した強化学習が起こっているのではないかと思われます。
ED法は文字認識などには弱いですが、論理学習には非常に優れた性能を発揮しますので、強化学習による行動学習には非常に向いていると思われます。強化学習による行動学習メカニズム(筆者予想)
1生体がある条件下にいる
2 前頭前野において、各コラムが競合し最も出力の高いユニットに対応する行動が選択される
3 選択された生物の行動(オペラント行動)が起こる
4 行動の結果、正の強化信号もしくは負の強化信号を受ける
5 アミン系を介して強化信号が反応したコラムにフィードバックされる
6 ED法同様のメカニズムで対応行動コラムの反応率が増加、もしくは減少する
ということが起こると思われます。
これを外部から観測すると、行動分析学での分析結果になると思われます。
ということは、将来的には、これのシミュレーションが可能になるでしょう。
究極的には、生物の行動を計算で求めることができるということですね>計算行動学?
文章から読み取るにED法版DQNでしょう。
2の"最も出力の高いユニット"は行動価値(Q-Network)を指して、"強化信号"は報酬に読み替えることができます。
どちらかというと実際の脳の解明に役立ちそうな情報のような?
最後に
とまあここまでED法を調べてみましたが、概要と性能もだいたい分かったので個人的には満足です。(記事としては最後かな)
見てわかる通りBPとは違った特性があり、BPで得意な領域、ED法で得意な領域というのがある気がします。
もし20年前にBPではなくED法が流行ればこっちが主流だったかもしれません。
(BPは初期に勾配消失が問題になっていた時期があったのでそのタイミングに公開されていれば主流になっていたかも)
(その場合はBPが失われた技術になっていたかも?)
誰かが研究を進めて数年後にBP+ED法の超速学習手法とかが現れれば面白いな~
・本当にどうでもいい話
多分BPの正式名称は誤差逆伝搬法で、BP法というと誤差逆伝搬法法になります。
ただ、金子さんのアーカイブでもBP法という言葉が使われていたりと、気を抜くとBP法と言ってしまう…