この記事は自作している強化学習フレームワークの解説記事です。
はじめに
今までフレームワークを通じて様々な強化学習アルゴリズムを実装してきました。
今回その知識を生かしてオリジナルなアルゴリズムを考えてみたので記事にまとめてみます。
このアルゴリズムは以下の状況でかなりの精度を誇ります。
- マルコフ決定過程なモデル
- 状態が離散で現実的な数
- 行動が離散で現実的な数
※"現実的な数"というのは数に上限があり、その上限がそれほど大きくない場合を指します
基本アイデア
基本的なアイデアは探索(Exploration)と活用(Exploitation)の分離です。
強化学習では一般的に「探索と活用のトレードオフの問題」1があり、探索を優先すると報酬が少なくなり、活用を優先すると局所解に陥る可能性が高くなる問題があります。
私が過去に記事で取り上げた手法では、どれも探索と活用のバランスをとり学習を進めていました。
しかし一般的に機械学習をする場合、学習フェーズと実行フェーズは分かれていると思います。
なので、学習フェーズは探索のみに集中し、実行フェーズは活用のみを実施する事でより効率化できるのではないか?というのが基本アイデアとなります。
本手法の概要をざっくりいうと以下です。
- 内部報酬とUCB1の導入による探索の効率化
- モデルベースを用いた価値反復法による価値計算の最適化
・追記:記載を忘れいていたので
本手法は安全に学習できるオフポリシーを前提条件として最大限に生かし、探索方策と求めたい方策を完全に分けています。
アルゴリズムの説明
1. モデルベース強化学習
本手法はモデルベース強化学習も取り入れています。
なのでまずは近似モデル(近似マルコフ決定過程、Approximate Markov decision process: AMDP)を説明します。
といっても難しい事はなく、そのままMDPを表現しています。
MDPの要素は以下です。
\begin{align}
s &: 状態\\
a &: アクション\\
p(s'|s, a) &: sにてaを選んだ後にs'に遷移する確率\\
r(s,a,s') &: sにてaを選びs'に遷移した時に得る報酬(即時報酬・外部報酬)\\
d(s,a,s') &: sにてaを選びs'に遷移した後に終了する確率\\
\end{align}
コードにそのまま落とし込みます。
学習では実際に観測した値を元に、確率と期待値を計算します。
action_num = アクション数
class AMDP:
def __init__(self):
# [state][action][next_state]
self.trans = {} # 状態の遷移回数
self.reward_ext = {} # 外部報酬の期待値(即時報酬)
self.reward_int = {} # 内部報酬の期待値(後述)
self.done = {} # 終了確率
def update(self, batch):
state = batch["state"]
n_state = batch["next_state"]
action = batch["action"]
reward_ext = batch["reward_ext"]
reward_int = batch["reward_int"]
done = batch["done"]
# 初期化処理
self.init_state(state, action, n_state)
# (s,a) -> n_s に遷移した回数をカウント
self.trans[state][action][n_state] += 1
c = self.trans[state][action][n_state]
# 終了確率を計算(1)
done = 1 if done else 0
old_done_rate = self.done[state][action][n_state]
self.done[state][action][n_state] += (done - old_done_rate) / c
# 外部報酬の平均を計算(1)
old_reward_ext = self.reward_ext[state][action][n_state]
self.reward_ext[state][action][n_state] += (reward_ext - old_reward_ext) / c
# 内部報酬の割引平均を計算(2)
int_reward_discount = 0.9
old_reward_int = self.reward_int[state][action][n_state]
self.reward_int[state][action][n_state] = old_reward_int * int_reward_discount+ (reward_int - old_reward_int * int_reward_discount) / c
def init_state(self, state, action, n_state):
if state not in self.trans:
self.trans[state] = [{} for _ in range(action_num)]
self.reward_ext[state] = [{} for _ in range(action_num)]
self.reward_int[state] = [{} for _ in range(action_num)]
self.done[state] = [{} for _ in range(self.action_num)]
if n_state is not None and n_state not in self.trans[state][action]:
self.trans[state][action][n_state] = 0 # 回数
self.reward_ext[state][action][n_state] = 0.0 # 期待値
self.reward_int[state][action][n_state] = 1.0 # 未探索1 -> 探索済み0 で遷移
self.done[state][action][n_state] = 0.0 # 確率
次の状態の遷移確率 $p(s'|s, a)$ は以下のように計算できます。
N = sum(self.trans[state][act].values())
for next_state in self.trans[state][act].keys():
prob = self.trans[state][act][next_state] / N
(1)オンライン平均の計算
(1)はオンラインで平均を計算しています。
一般的な平均は以下です。
\bar{x}_n = \frac{\sum_{i=1}^{n} x_i}{n}
ただこれは計算に全データが必要で、今回みたいにデータを1つずつ与えられてかつリアルタイムに平均が欲しい場合の計算には不向きです。2
計算は割愛しますが以下に変形できるようです。
\bar{x}_{n+1} = \bar{x}_{n} + \frac{n_{x+1} - \bar{x}_{n}}{n + 1}
コードだと以下です。
import numpy as np
data = [1, 2, 3, 4, 5]
x = 0
n = 0
for i, d in enumerate(data):
n += 1
x = x + (d - x) / n
print(np.mean(data[: i + 1]), x)
"""
1.0 1.0
1.5 1.5
2.0 2.0
2.5 2.5
3.0 3.0
"""
参考
・https://ehbtj.com/electronics/average-online-algorithm/
・https://qiita.com/awakia/items/f58e90b3b2562d787aa5
(2)割引報酬
後述しますが内部報酬は価値が変動し、古い価値は信用できなくなります。
ですので新しい価値を重視するように割引報酬で計算します。
ここの計算アイデアはAgent57で登場したsliding-window UCB法が元になっています。
多腕バンディット問題で、報酬が変動する場合の手法としては大きく"sliding-window UCB"と"Discounted UCB"があるようです。
前者は直近の数回を対象として価値を推定するUCBですが、後者は減衰率を追加し重み付き報酬で価値を推定するUCBです。
内部報酬は毎ステップ価値が変動するので"Discounted UCB"を採用しています。
2. 方策反復法
マルコフ決定過程のモデルができたのでこれを元にベルマン方程式を解きます。
ベルマン方程式は以下でした。
$$
Q_{\pi}(s,a) = \sum_{s'} p(s'|s,a) \Big(r(s,a,s') + \gamma \sum_{a'} \pi(a'|s') Q_{\pi}(s', a') \Big)
$$
$Q_{\pi}$は方策$\pi$における行動価値、$\gamma$は割引率、$\pi(a|s)$は方策$\pi$上で状態$s$にて行動$a$を選ぶ確率です。
ベルマン方程式は再帰構造になっているので解くのが難しいですが、逆に言えば再帰してしまえば解けます。
なので動的計画法で行動価値を求めます。(これを方策反復法といいます)
方策反復法にて重要なのが方策で、求めたい方策を事前に決める必要があります。
方策の例として、Q学習では常に行動価値が高いアクションを選ぶ方策をとっており、SARSAではε-greedyに従った方策をとっています。
本アルゴリズムでは外部報酬はQ学習と同様に常に行動価値が高いアクションを選ぶ方策にします。(後述しますが、内部報酬は別の方策です)
その場合のベルマン方程式は以下です。
Q^{max}_{\pi}(s,a) = \sum_{s'} p(s'|s,a) \Big(r(s,a,s') + \gamma \max_{a'} Q^{max}_{\pi}(s', a') \Big)
ここで $\max_{a'} Q^{max}_{\pi}(s', a')$ は行動価値が一番高いアクションの行動価値を表しています。
方策反復法を実装したコードは以下です。
amdp = AMDP() # 近似モデル
q_ext_tbl = {} # Qテーブル
discount = 0.9 # 割引率
action_num = アクション数
def iteration_q_ext(threshold: float=0.0001):
for _ in range(100): # for safety
delta = 0
# 全ての状態、アクションに対して走査する
for state in amdp.trans.keys():
# Qテーブル初期化処理
if state not in q_ext_tbl:
q_ext_tbl[state] = [0.0 for a in range(action_num)]
for act in range(action_num):
N = sum(amdp.trans[state][act].values())
if N == 0:
continue
# 行動価値Qを計算する
q = 0
for next_state in amdp.trans[state][act].keys():
if amdp.trans[state][act][next_state] == 0:
continue
# Qテーブル初期化処理
if next_state not in q_ext_tbl:
q_ext_tbl[next_state] = [0.0 for a in range(action_num)]
# 次の状態の遷移確率
trans_prob = amdp.trans[state][act][next_state] / N
# 取得する報酬の期待値
reward = amdp.reward_ext[state][act][next_state]
# 終了確率
done = amdp.done[state][act][next_state]
# 次の状態の最大行動価値
n_q = np.max(q_ext_tbl[next_state])
# ベルマン方程式
gain = reward + (1 - done) * discount * n_q
q += trans_prob * gain
# 終了判定用に更新幅を取得
delta = max(delta, abs(q_ext_tbl[state][act] - q))
# Qを更新
q_ext_tbl[state][act] = q
# 更新幅が閾値以下になったら終了
if delta < threshold:
break
else:
print("iteration over")
3. 内部報酬
内部報酬の目的はまだ見ていない状態に積極的に訪れることです。
これを、未知の状態の価値を高く見積もることで実現します。
考え方はNGU/Agent57を参考に、エピソード記憶部と生涯記憶部から実現します。
3-1. エピソード記憶部(episodic novelty module)
エピソード記憶部では1エピソード内で同じ状態を訪れないように報酬を決めます。
計算式は以下です。
$$
r^{episode} = \frac{1}{ \sqrt{n(s)+1} }
$$
$n(s)$ は状態$s$に訪れた回数となります。
3-2. 生涯記憶部(life long novelty module)
生涯記憶部は学習全体で同じ状態を訪れないようにします。
初期値を1とし、訪れる毎に割合で減らしていきます。
3-3. 内部報酬
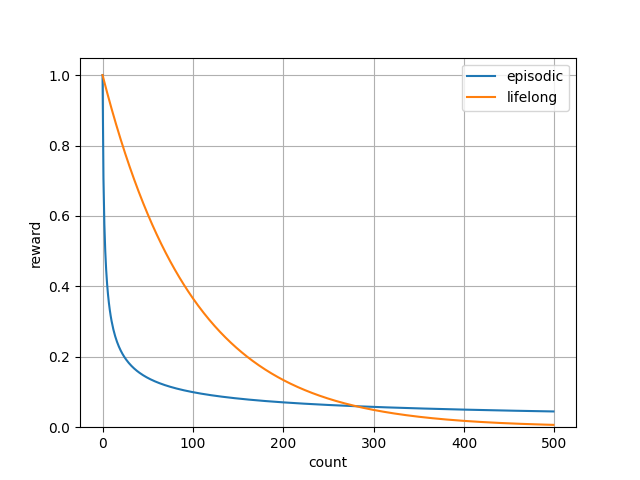
エピソード記憶部と生涯記憶部を可視化すると以下です。
エピソード記憶部の方が強く働くようにし、生涯記憶部の方がゆっくり働くようにしています。
また感覚的に分かりやすいように両方とも0~1の範囲にしました。
最終的な内部報酬はこの2つを乗算します。
episodic = {}
lifelong = {}
lifelong_decrement_rate = 0.99
def calc_episodic_reward(state):
if state not in episodic:
episodic[state] = 0
# 0回だと無限大になるので1回は保証する
reward = 1 / math.sqrt(episodic[state] + 1)
episodic[state] += 1
return reward
def calc_lifelong_reward(state):
if state not in episodic:
lifelong[state] = 1
reward = lifelong[state]
# lifelong[state] *= lifelong_decrement_rate # 実際の更新はtrainerで
return reward
episodic_reward = calc_episodic_reward(state)
lifelong_reward = calc_lifelong_reward(state)
reward_int = episodic_reward * lifelong_reward
3-4. 内部報酬の方策
ベルマン方程式における内部報酬の方策ですが、これは行動価値が高いものを選ぶのではなく、ある程度ランダム性を持たせます。
ランダム性を持たせた理由ですが、実際に行動価値が高いもので試してみたところ、どうやら局所解に入るらしく探索が進まない状況がありました。
多分ですが、これは内部報酬の目的が価値を最大にする事ではなく、探索の効率化を目的としているので、アクションの見る方向が1方向(最大のアクションのみ)を見るよりかは周囲をある程度見たほうが探索に貢献できるのではないかと考えています。
具体的な方策は価値が最大のものは $p$% で、それ以外は $\frac{1-p}{残りのアクション数}$%で選択されるとします。(一応p=90%を想定)3
コード例は以下です。
amdp = AMDP() # 近似モデル
q_int_tbl = {} # Qテーブル
discount = 0.9 # 割引率
policy_prob = 0.9 # 方策の確率
action_num = アクション数
def iteration_q_int(threshold: float=0.0001):
for _ in range(100): # for safety
delta = 0
# 全ての状態、アクションに対して走査する
for state in amdp.trans.keys():
# Qテーブル初期化処理
if state not in q_int_tbl:
q_int_tbl[state] = [0.0 for a in range(action_num)]
for act in range(action_num):
N = sum(amdp.trans[state][act].values())
if N == 0:
continue
# 行動価値Qを計算する
q = 0
for next_state in amdp.trans[state][act].keys():
if amdp.trans[state][act][next_state] == 0:
continue
# Qテーブル初期化処理
if next_state not in q_int_tbl:
q_int_tbl[next_state] = [0.0 for a in range(action_num)]
# 次の状態の遷移確率
trans_prob = amdp.trans[state][act][next_state] / N
# 取得する報酬の期待値
reward = amdp.reward_int[state][act][next_state]
# 終了確率
done = amdp.done[state][act][next_state]
# 次の状態の行動価値を計算
q_max_idx = np.argmax(q_int_tbl[next_state])
n_q = 0
for a in range(action_num):
if a == q_max_idx:
p = policy_prob
else:
p = (1 - policy_prob) / (action_num - 1)
n_q += p * q_int_tbl[next_state][a]
# ベルマン方程式を計算
gain = reward + (1 - done) * discount * n_q
q += trans_prob * gain
# 終了判定用に更新幅を取得
delta = max(delta, abs(q_int_tbl[state][act] - q))
# Qを更新
q_int_tbl[state][act] = q
# 更新幅が閾値以下になったら終了
if delta < threshold:
break
else:
print("iteration over")
4. 経験の収集と方策
経験収集の方策ですが、よく使われるε-greedyではなくUCB1で決定します。
またUCB1で使う期待報酬は、外部報酬による行動価値と内部報酬による行動価値両方を使います。
なぜ外部報酬も使うかというと、内部報酬が同じ場合、外部報酬が高い周辺を重点的に探索してほしいからです。
UCB1(Upper Confidence Bound 1)の式は以下です。
$$
\frac{w}{n} + \beta \sqrt{ \frac{ \ln{N} }{n} }
$$
$w$が勝利数、$n$が選択回数、$N$が全選択回数、$\beta$が定数で$\sqrt{2}$です。
基本はこの数式を使いますが、スケールを合わせるために一工夫追加します。
UCB1の左項 $\frac{w}{n}$ は勝率が前提となっており、$[0,1]$の範囲を取ります。
行動価値は取りうる値に制限がないので、$[0,1]$の範囲で正規化してからUCB1を適用します。
コード例は以下です。
action_count = {} # [state][action], 選択したアクションの回数を数えるテーブル
action_num = アクション数
ucb_beta = np.sqrt(2) # 実際は、勝率は内部報酬(探索率)なのでβはもっと小さい値でもいい
search_rate = 0.5
def policy(state: 現在の状態):
# 正規化用に最大値と最小値を取得
# (pythonは、min/maxはテーブル形式に対して使えないのでエラーになります。なのでコードはイメージです)
# (実際はQテーブル更新時に更新してキャッシュ)
q_ext_mix = min(q_ext_tbl)
q_ext_max = max(q_ext_tbl)
q_int_mix = min(q_int_tbl)
q_int_max = max(q_int_tbl)
q_ext = np.array(q_ext_tbl[state]) # 外部報酬の行動価値
q_int = np.array(q_int_tbl[state]) # 内部報酬の行動価値
# [0,1]に正規化(min==maxの場合は正規化しない、コードは省略)
q_ext = (q_ext - q_ext_min) / (q_ext_max - q_ext_min)
q_int = (q_int - q_int_min) / (q_int_max - q_int_min)
# 外部報酬がmin==maxの場合は疎な環境なので内部報酬のみ使う
if q_ext_min >= q_ext_max:
q = q_int
else:
q = (1-search_rate)*q_ext + search_rate*q_int
# UCBを計算し、アクションを決める
N = sum(action_count[state])
ucb_list = []
for a in range(action_num):
n = action_count[state][a]
if n == 0:
ucb_list.append(np.inf)
else:
ucb = q[a] + ucb_beta * np.sqrt(np.log(N) / n)
self.ucb_list.append(ucb)
action = np.argmax(ucb_list) # 実際のコードでは最大値が複数ある場合は乱数で選択
action_count[state][action] += 1 # 数える
return action
追記:
後から記事を見返してふと思いましたが、この方策はε-greedyにする考えも残っていますね。
元々はアクションを選択する問題を多腕バンディット問題と考えており、Regretを最小化しているアルゴリズム(Regretが下限=上限信頼限界だと理論上最も性能がいいアルゴリズム)を採用したくUCB1を選びました。
(UCB1はRegret下限で、ε-greedyはRegret下限ではない)
しかし今回の場合では、実際に得る内部報酬の最大化を目指しておらず(Regretの下限は総報酬の最大化を指す)、内部報酬の高いエリアに移動したいというモチベーションなので考察の余地があるかもです。
探索の全体イメージ(Worker)
探索サイクルを書くと以下です。
class Worker:
def reset(self, state):
# episodeの最初にエピソード記憶部用のtblを作成
self.episodic = {}
def policy(self, state):
# UCB1でアクションを決める(コードは省略)
self.action = action
return action
def on_step(self, next_state, reward, done):
# 内部報酬を計算
episodic_reward = calc_episodic_reward(next_state)
lifelong_reward = calc_lifelong_reward(next_state)
reward_int = episodic_reward * lifelong_reward
# memoryにbatchを送信
batch = {
"state": self.state,
"next_state": next_state,
"action": self.action,
"reward_ext": reward,
"reward_int": reward_int,
"done": done,
}
self.memory.add(batch)
SequenceMemory
batchの送信に使うmemoryですが、近似モデルで確率を求めるために使われるのでbatchを使いまわす事ができません。
ですので Experience Replay や Priority Experience Replay は使わず、batchを1回のみ使う形となります。
5. 学習
収集した経験を元に、近似モデル、内部報酬で使う生涯記憶部、外部報酬の行動価値、内部報酬の行動価値を学習します。
行動価値は方策反復法でも学習しますが、一部の状態しかモデルが更新されてないのにすべての状態に対して計算しなおすのはコストが高いので、TD誤差による学習も同時に行います。
(TD誤差による学習に関しては過去に書いた価値ベースアルゴリズムの基礎(Q学習)を見てください)
コード例は以下です。
amdp = AMDP()
lifelong = {} # [state]
lifelong_decrement_rate = 0.99
q_ext_tbl = {} # [state][action]
q_int_tbl = {} # [state][action]
q_ext_discount = 0.9
q_ext_lr = 0.1
q_int_discount = 0.9
q_int_lr = 0.1
iteration_interval = 1000
def train(batch):
state = batch["state"]
n_state = batch["next_state"]
action = batch["action"]
reward_ext = batch["reward_ext"]
reward_int = batch["reward_int"]
done = batch["done"]
# ※初期化処理は省略
amdp.update(batch) # amdp update
lifelong[state] *= lifelong_decrement_rate # lifelong update
# --- ext
target_q = reward_ext
if not done:
n_q = max(q_ext_tbl[n_state])
target_q += q_ext_discount * n_q
td_error_ext = target_q - q_ext_tbl[state][action]
q_ext_tbl[state][action] += q_ext_lr * td_error_ext
# --- int
target_q = reward_int
if not done:
# 確率に従って次の状態価値(期待値)を計算
policy_prob = 0.9
n_q = 0
q_max = max(q_int_tbl[n_state])
for a in range(action_num):
if q_int_tbl[n_state][a] == q_max:
p = policy_prob
else:
p = (1 - policy_prob) / (action_num - 1)
n_q += p * q_int_tbl[n_state][a]
target_q += q_int_discount * n_q
td_error_int = target_q - q_int_tbl[state][action]
q_int_tbl[state][action] += q_int_lr * td_error_int
# 一定期間ごとに方策反復法で計算する
if train_count % iteration_interval == 0:
iteration_q_ext()
iteration_q_int()
train_count += 1
性能比較
比較はQ学習と行います。
それぞれの実装コードはgithubを見てください。
・Q学習
・SearchDynaQ
※以下動作コードですが、SRLがv0.14.1で確認しているコードとなります。
Grid
いつもの環境です。(コードはこちら)
ゴールに行くと1の報酬、穴に落ちると-1の報酬で、アクションと同じ方向に移動できる確率は80%です。
この環境の最適な行動価値(Qテーブル)は以下です。
Q学習と本手法(SearchDynaQ)のQテーブルを比較してみます。
-------------------------------------------------------
0.523 | 0.650 | 0.801 | 0.000
0.498 0.610| 0.537 0.766| 0.648 0.928| 0.000 0.000
0.435 | 0.650 | 0.554 | 0.000
-------------------------------------------------------
0.487 | 0.000 | 0.585 | 0.000
0.399 0.399| 0.000 0.000| 0.503 -0.686| 0.000 0.000
0.317 | 0.000 | 0.224 | 0.000
-------------------------------------------------------
0.374 | 0.267 | 0.428 | -0.753
0.307 0.273| 0.288 0.327| 0.286 0.187| 0.189 0.017
0.292 | 0.267 | 0.314 | 0.151
-------------------------------------------------------
Q学習で1000回学習した後のQテーブルは以下です。
-------------------------------------------------------
-0.026 | 0.145 | 0.347 | 0.000
-0.027 0.270| 0.066 0.627| 0.162 0.902| 0.000 0.000
0.030 | -0.008 | 0.286 | 0.000
-------------------------------------------------------
0.076 | 0.000 | 0.568 | 0.000
-0.050 -0.050| 0.000 0.000|-0.006 -0.172| 0.000 0.000
-0.051 | 0.000 | -0.036 | 0.000
-------------------------------------------------------
-0.047 | -0.008 | 0.386 | -0.190
-0.064 0.148|-0.030 0.266| 0.003 -0.032| 0.091 -0.096
-0.018 | -0.011 | 0.065 | -0.100
-------------------------------------------------------
Q学習は報酬の伝搬に時間がかかります。
ゴール付近は環境の行動価値に近いですが、スタート地点はまだ伝搬しきっていないので値がおかしいですね。
同じくSearchDynaQで、1000回学習した後に方策反復法を使った後のQテーブルは以下です。
-------------------------------------------------------
0.621 | 0.734 | 0.860 | 0.000
0.621 0.734| 0.621 0.860| 0.734 1.000| 0.000 0.000
0.435 | 0.734 | 0.734 | 0.000
-------------------------------------------------------
0.528 | 0.000 | 0.860 | 0.000
0.435 0.435| 0.000 0.000| 0.734 -1.000| 0.000 0.000
0.364 | 0.000 | 0.621 | 0.000
-------------------------------------------------------
0.426 | 0.482 | 0.734 | 0.621
0.343 0.404| 0.350 0.528| 0.634 0.519| 0.621 0.519
0.343 | 0.528 | 0.621 | 0.519
-------------------------------------------------------
確率的な遷移があるので探索不足な箇所では値が違いますが、全状態で環境の行動価値にかなり近い値になっています。
・コード
import srl
from srl.algorithms import ql, search_dynaq
from srl.envs import grid
env = grid.Grid()
Q = env.calc_action_values()
env.print_action_values(Q)
runner = srl.Runner("Grid", ql.Config())
runner.train(max_train_count=1000)
print(runner.evaluate(10))
env.print_action_values(runner.parameter.Q)
runner = srl.Runner("Grid", search_dynaq.Config())
runner.train(max_train_count=1000)
print(runner.evaluate(10))
env.print_action_values(runner.parameter.q_ext)
FrozenLake
Gymで提供されているFrozenLakeで見てみます。
Gridと似ていますが、移動できる確率は33%でゴールにしか報酬がありません。(穴に落ちても0)
なので報酬が疎な環境となります。
参考までに最適な行動は以下となります。(基本穴の方向に行動するのは悪手となります)
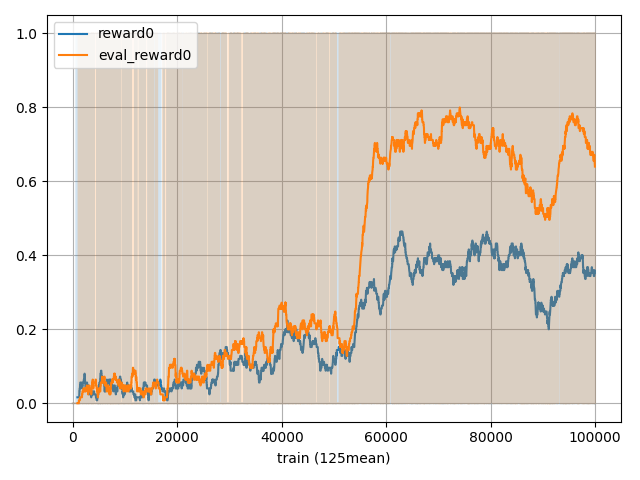
Q学習の結果は以下で、青が学習時の報酬でオレンジが評価時の報酬です。
学習が60000回あたりから学習できているようですね。
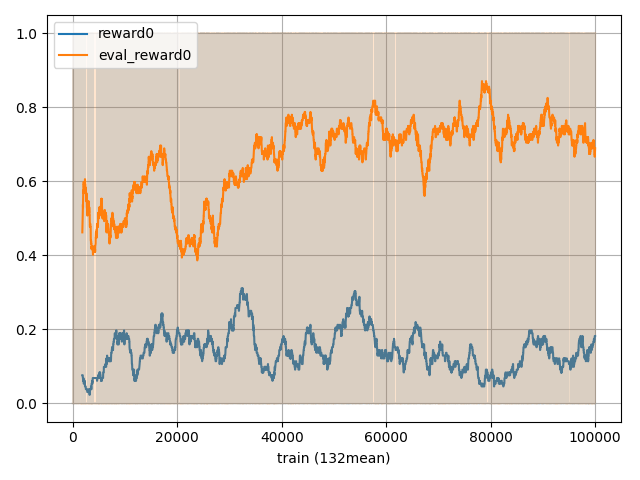
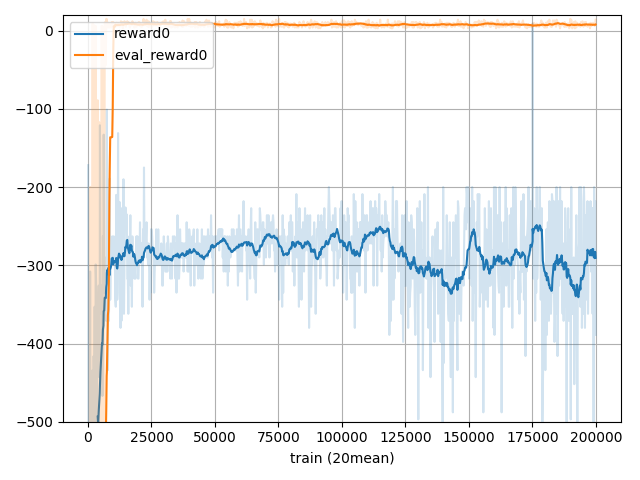
次にSearchDynaQの結果は以下です。
最初の段階で報酬は0.4を超えており、40000回あたりで学習を終えていそうですね。
また、青(探索時の報酬)がずっと低い報酬なのは探索を優先しているからとなります。
・コード
すぐ学習するので学習率を下げています。
import numpy as np
import srl
from srl.algorithms import ql, search_dynaq
def train(rl_config):
runner = srl.Runner("FrozenLake-v1", rl_config)
runner.set_history_on_memory(
interval=1,
interval_mode="step",
enable_eval=True,
eval_episode=1,
)
runner.train(max_train_count=100_000)
rewards = runner.evaluate(max_episodes=100)
print(f"{np.mean(rewards)}")
runner.get_history().plot("train", ylabel_left=["reward0", "eval_reward0"])
train(ql.Config(lr=0.03))
train(search_dynaq.Config(q_ext_lr=0.03, q_int_lr=0.03))
Taxi
同じくGymで提供されているTaxiで見てみます。
Taxiは移動が決定的なのでFrozenLakeより行動選択はわかりやすいです。
ただ初期状態がランダムで状態数が多く(500ほどらしい)、報酬が-10,-1,+20の3種類とスケールがだいぶ違うのが特徴です。
・Q学習
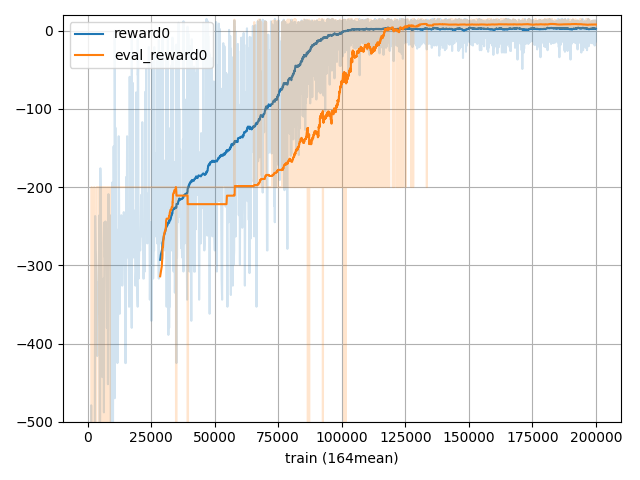
マイナスの総報酬が-1000ぐらいまでいくので見やすいように-500から表示するようにしています。
125000回あたりから正の報酬が獲得できるようになっていますね。
・SearchDynaQ
青(探索)の報酬は-300ぐらいですが、オレンジは25000回の時点ですでに正の報酬が獲得できていますね。
・コード
import numpy as np
import srl
from srl.algorithms import ql, search_dynaq
def train(rl_config):
runner = srl.Runner("Taxi-v3", rl_config)
runner.set_history_on_memory(
interval=1,
interval_mode="step",
enable_eval=True,
eval_episode=1,
)
runner.train(max_train_count=200_000)
rewards = runner.evaluate(max_episodes=100)
print(f"{np.mean(rewards)}")
runner.get_history().plot(
"train",
ylabel_left=["reward0", "eval_reward0"],
left_ymin=-500,
left_ymax=20,
)
train(ql.Config())
train(search_dynaq.Config())
Oneroad
最後に報酬がかなり疎な環境で見てみます。(コードはこちら)
この環境はアクションが20個あり、初期状態が0です。
アクションの0を選ぶと状態が+1されて20まで行くと報酬1が手に入ります。
しかし0以外のアクションを選ぶと状態が0に戻されます。
要するにアクション0を20回連続で選ばないと報酬が得られない環境です。
ε-greedyを採用しているQ学習では相当運が良くないと報酬を得られません。
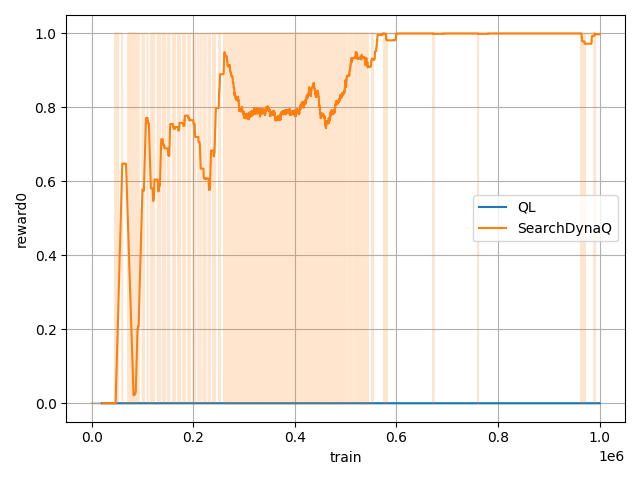
1_000_000回学習する場合のQ学習とSearchDynaQの結果を見てみました。
どちらも探索中の報酬です。
SearchDynaQは50_000回あたりで報酬を得ていますが、Q学習は1_000_000回実行しても報酬は得られていません。
これは内部報酬による探索がかなり効いている結果だと思われます。
・コード
import os
import numpy as np
import srl
from srl.algorithms import ql, search_dynaq
base_dir = os.path.dirname(__file__)
def train(name, rl_config):
runner = srl.Runner("OneRoad-hard", rl_config)
runner.set_history_on_file(
os.path.join(base_dir, f"_{name}"),
interval=1,
interval_mode="step",
)
runner.train(max_train_count=1_000_000)
rewards = runner.evaluate(max_episodes=100)
print(f"{np.mean(rewards)}")
def compare():
names = [
"QL",
"SearchDynaQ",
]
histories = srl.Runner.load_histories(
[os.path.join(base_dir, f"_{n}") for n in names]
)
histories.plot("train")
train("QL", ql.Config())
train("SearchDynaQ", search_dynaq.Config())
compare()
最後に
アルゴリズムの内容は結構右往左往しましたが、思ったよりまとまった形にできました。
内容は古典的な強化学習ですが、各手法は今まで学んだことの集大成みたいな感じで満足できるアルゴリズムができました。
前提条件さえ満たせば最強なアルゴリズムではなかろうか