身近な場面で、浮動小数点絡みの問題に遭遇したので、その話をシェアしたいと思います。
後輩からの質問「ヒストグラムが上手く描けない」
後輩から質問が来ました。
「ヒストグラムが上手く描けない」とのことでした。
グラフ作成ライブラリmatplotlibでヒストグラムを書こうとして、失敗したようです。
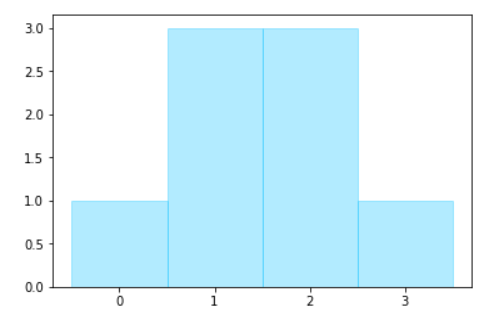
後輩が描こうとしたヒストグラムがこちら。
import matplotlib.pyplot as plt
import numpy as np
s = np.array([0, 1, 1, 1, 2, 2, 2, 3])
mins = s.min()
maxs = s.max()
plt.hist(s, bins=int(maxs - mins + 1), range=(mins, maxs+1), alpha=0.3, color='deepskyblue', ec='deepskyblue', align='left')
plt.xticks(np.arange(mins, maxs+1, step=1))
これは、上手く描けている例です。
いつもは、このやり方で描けていたのに、今日は上手く描けなかったので、私のところに質問に来たようです。
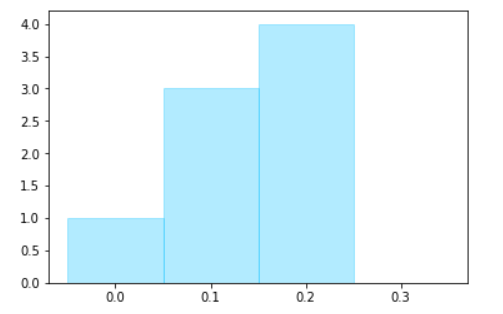
その例がこちら。
import matplotlib.pyplot as plt
import numpy as np
s = np.array([0, 0.1, 0.1, 0.1, 0.2, 0.2, 0.2, 0.3])
mins = s.min()
maxs = s.max()
plt.hist(s, bins=int((maxs-mins)*10 + 1), range=(mins, maxs+0.1), alpha=0.3, color='deepskyblue', ec='deepskyblue', align='left')
plt.xticks(np.arange(mins, maxs+0.1, step=0.1))
基本的に、スケールが違う点以外は、初めの例と同じです。
変数の値をprintしてみましたが、一見おかしな所は見つかりませんでした。
print(s) # data
print(int((maxs-mins)*10 + 1)) # bin
print(mins) # range
print(maxs+0.1) # range
print(maxs)
出力:
[0. 0.1 0.1 0.1 0.2 0.2 0.2 0.3]
4
0.0
0.4
0.3
この結果を見て、私も「なぜ?」と思いました。
そして、もう少し調べてみることにしました。
答え「浮動小数点」
さらに突っ込んで変数の中身を見てみると、変数maxsは、一見0.3の値が正確に入っているように見えるが、実は厳密には0.3とは異なる値が入っていることが分かりました。
その証拠がこちら
print(maxs)
print(type(maxs))
print(maxs/3.0)
出力:
0.3
class 'numpy.float64'
0.09999999999999999
s = np.array([0, 0.1, 0.1, 0.1, 0.2, 0.2, 0.2, 0.3])に対して、s.max()で最大値を取った値を3で割っても、0.1になっていません。
これは、sの最大値、maxsがnumpy.float64型という、64bitの浮動小数点で表されているためです。表示上は、maxsに正確に0.3の値が入っているように見えていましたが、マシン内部では、2進数の近似値で保持されており、厳密には0.3と違う値が入っていたのです。
※pythonの浮動小数点の扱いに関する詳細はこちら
今回の例では、0.3なのか、0.29999999999999999なのかという微妙な違いが影響して、上手くヒストグラムが描画できなかった、ということが分かりました。
今後への教訓
数値計算のプログラムを書いていると、閾値判定で処理を分岐するというケースもあるかと思います。その時に、浮動小数点の問題を意識せずにコーディングすると、思いもよらない結果になりそうです。
float型での演算を繰り返した後で、境界値で閾値判定を行うのは危険、ということを再認識しました。
参考
[15. 浮動小数点演算、その問題と制限]
(https://docs.python.jp/3/tutorial/floatingpoint.html)