Parsletで構文解析する[その2]
ここまで
その1基本的なルールと簡単な数値リテラルパーサを作った。
Parsletサンプル
もうちょっと複雑な構文をパース
[その1]で単純なリテラルに関してはパースできるようになったので、次は定番の四則演算をパースできるようにしましょう。
加減算のみでパース
乗除算が入ってくると演算子の優先順位などが出てくるので、まずは加減算のみパースできるようにします。
その前に何点か前置きを、
- 結合順
演算子には結合順序があり、例えば加減算だと一般的には左結合と呼ばれ、左から順にくくられることになります。
具体的には
1 + 2 + 3 + 4
が
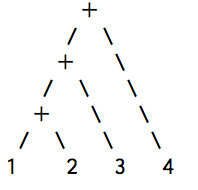
とみなされるということです。こういった処理はよくあるので、Parsletでもこれ専用のルールがあるのですが、自分で組んでから使ったほうがよく分かるのでまずは手動でパースして、あとでその専用ルールに置き換えてみようと思います。
- 空白文字の考慮
もう一点、 空白の扱いですが、数式としては、(半角スペースを _とすると) 1_+_2_+_3 も 1+2_+_3 も 1+2+3 も同じ意味になりますね。
raccとかyaccとかだと構文解析の前にtokenに分ける字句解析器的なフェーズがあるのですが、parsletの場合、構文のルールの中に字句解析も含むので適当に空白の考慮をいれていきます。
Parslet公式のサンプルでもよく出てくる空白のルールも定義しておきます。
# 空白文字一文字以上が連続した文字列にマッチするルール
rule(:space) { match('\s').repeat(1) }
# 空白文字列があればそれにマッチするルール
rule(:space?) { space.maybe }
加減算パーサの作成
先程の空白を考慮して、各tokenの末尾にゼロ個以上の空白文字列があれば無視する方針で定義し直してみます。
- 数値リテラルの定義
末尾に >> space? をいれて、数値リテラル以降の空白文字もマッチするようにします。
rule(:number) {
sign.maybe >> integer >> decimal.maybe >> space?
}
- 演算子文字の定義
これも数値と同様に+,-の文字のあとの空白文字列を読み飛ばすように定義します。
rule(:exp_op) { match('[+-]') >> space? }
- 加減算の定義
↑でみたように 1 + 2 - 3 + ... のように加減算を無限に連結できる一方、 式としては 1 といった数値単独もありなので、
数値 の後に (演算子 + 数値)の組が0個以上繰り返される
という形で定義してみます。
rule(:exp) { number >> (exp_op >> number).repeat }
加減算パーサ全体
全体としては下記のようになります。
require 'parslet'
class CalcParser < Parslet::Parser
rule(:sign) { match('[-+]') }
rule(:integer) {
(match('[1-9]') >> match('[0-9]').repeat) |
match('[0-9]')
}
rule(:decimal) {
str('.') >> match('[0-9]').repeat
}
rule(:number) {
sign.maybe >> integer >> decimal.maybe >> space?
}
rule(:exp) { number >> (exp_op >> number).repeat }
rule(:exp_op) { match('[+-]') >> space? }
rule(:space) { match('\s').repeat(1) }
rule(:space?) { space.maybe }
root(:exp)
end
p CalcParser.new.parse('1+2-3')
# => "1+2-3"@0
p CalcParser.new.parse('1+2-')
# => Parslet::ParseFailed -の項が足りないのでエラーが出る
正しい加減算はパースでき、おかしなものはパースエラーになりました。
ですが、パース結果("1+2-3@0"を見ると、せっかくパースした数値リテラルや、演算子、その繰り返しなどの情報がありません。
次でその各要素を識別する方法に関して見てみます。
パース結果のキャプチャ
各文法ルールはそのマッチした内容に as メソッドでパース結果に名前をつけることができます。
ここでは、左辺、演算子、右辺、ということで、expに下記のように名前をつけてみます。
require 'parslet'
class CalcParser < Parslet::Parser
rule(:sign) { match('[-+]') }
rule(:integer) {
(match('[1-9]') >> match('[0-9]').repeat) |
match('[0-9]')
}
rule(:decimal) {
str('.') >> match('[0-9]').repeat(1)
}
rule(:number) {
sign.maybe >> integer >> decimal.maybe >> space?
}
# expの各要素のマッチ結果をasでキャプチャする
rule(:exp) { number.as(:left) >> (exp_op.as(:op) >> number.as(:right)).repeat }
rule(:exp_op) { match('[+-]') >> space? }
rule(:space) { match('\s').repeat(1) }
rule(:space?) { space.maybe }
root(:exp)
end
p CalcParser.new.parse('1 + 2 - 3')
# => [{:left=>"1 "@0}, {:op=>"+ "@2, :right=>"2 "@4}, {:op=>"- "@6, :right=>"3"@8}]
いい感じに見えますが
{:left=>"1 "@0}
というように、numberルール自体にspace?の考慮が入っているため、左辺として空白まで含まれてしまっています。これだと面倒なので、純粋に意味のある部分にasで名前をつけるように変更します。
また、あとで処理しやすいようにexp全体にも名前をつけておきます。
require 'parslet'
class CalcParser < Parslet::Parser
rule(:sign) { match('[-+]') }
rule(:integer) {
(match('[1-9]') >> match('[0-9]').repeat) |
match('[0-9]')
}
rule(:decimal) {
str('.') >> match('[0-9]').repeat(1)
}
rule(:number) {
# 数値部分に対して :number でキャプチャする
(sign.maybe >> integer >> decimal.maybe).as(:number) >> space?
}
# 数値や演算子は各レベルでキャプチャしているので、ここでは左辺、右辺のキャプチャのみ
rule(:exp) { (number.as(:left) >> (exp_op >> number.as(:right)).repeat).as(:exp) }
# 演算子に対して :op でキャプチャする
rule(:exp_op) { match('[+-]').as(:op) >> space? }
rule(:space) { match('\s').repeat(1) }
rule(:space?) { space.maybe }
root(:exp)
end
p CalcParser.new.parse('1 + 2 - 3')
# => {:exp=>[{:left=>{:number=>"1"@0}}, {:op=>"+"@2, :right=>{:number=>"2"@4}}, {:op=>"-"@6, :right=>{:number=>"3"@8}}]}
これでパース結果が
{:exp=>[{:left=>{:number=>"1"@0}}, {:op=>"+"@2, :right=>{:number=>"2"@4}}, {:op=>"-"@6, :right=>{:number=>"3"@8}}]}
となり、空白は無視され、意味のあるtokenだけがパース結果として抽出されています。
パース後のTransform
先程まででただの文字列を一定の規則に従って、解析できるところまでできるようになりました。
ただ、結果としては、
{:exp=>[{:left=>{:number=>"1"@0}}, {:op=>"+"@2, :right=>{:number=>"2"@4}}, {:op=>"-"@6, :right=>{:number=>"3"@8}}]}
というような複雑な形になっており、このまま計算するのは大変です。これを先程示したような木構造
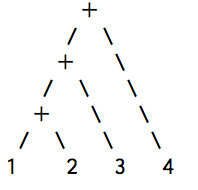
のような形のデータ構造になおすことができれば、そのまま計算できますね。
Parsletでは構文解析の結果できたHash的な構造をさらに任意のオブジェクト構造に変換する仕組みが用意されており、その変換をTransformと呼んでいます。
このTransformの結果を各ドメインロジックのオブジェクトとして構築し、必要な処理、結果を得ることができます。
今回の加減算では、
- parse処理
"1+2-3"というようなただの文字列をruleに従って解析 - transform処理
パーサの結果を受けて、計算しやすい木構造に変換 - ドメインロジック
実際に加減算を行って結果を得る
という流れになります。
transformのテンプレート
# Parslet::Transformを継承する(Parslet::Transformを直接使う方法もありますが略)
class CalcTransform < Parslet::Transform
# transform用のruleを定義し、そのルールにマッチしたものの変換する処理を定義する
rule(number: simple(:x)) { x.to_f }
end
# パース結果を引数にTransformオブジェクトのapplyを実行すると上記のruleに従って構文解析結果が変換される
CalcTransform.new.apply(パーサのパース結果のオブジェクト)
parserでは、生の文字列に対する変換ルールを定義していたのに対して、transformでは、parserの処理結果に対する変換ルールを定義する、という感じですね。
transformのルール
transformのルールは基本的に
rule(symbol(キャプチャ結果のシンボル): type(そのキーに対応するオブジェクトのタイプ)) { 変換処理 }
または
rule(type(そのキーに対応するオブジェクトのタイプ)) { 変換処理 }
(この2つというより、ruleの引数に渡された構造(配列やハッシュ)とパターンマッチされるようなイメージです)
という形式になります。 symbol は先程見た as でのキャプチャキーのことです。
typeについては、simple, sequence, subtree の3種類があり、
| ルール名 | 内容 |
|---|---|
| simple | symbolに対する値が配列でも、ハッシュでもない場合 |
| sequence | symbolに対する値がsimpleにマッチする要素のみでできた配列の場合 |
| subtree | symbolに対する値が上記以外の場合 |
という条件にマッチするものが、構文解析結果の末端(木構造での葉の部分から)繰り返し適用されていきます。
ただし、同じsymbolに対して、subtreeと、subtree以外が定義されていた場合、 全部subtree側に取られてしまうのでいろいろ試してみてください。
rule がマッチした場合の具体的な変換処理で、上記のルールに渡したシンボルがブロック内でのローカル変数として使用できます。
require 'parslet'
class TransformTest < Parslet::Transform
# 確認のために同一のキーで各typeを定義してその内容(x)をそのままダンプする
rule(k1: simple(:x)) {
puts("match simple")
p x
}
rule(k1: sequence(:x)) {
puts("match sequence")
p x
}
# これをk1で定義してしまうと全部このルールにマッチしてしまうため
# これだけk2で定義する
rule(k2: subtree(:x)) {
puts("match subtree")
p x
}
# 下記のようにt1、t2それぞれのキーに対してそれぞれの種類でマッチする
# ようなルールも作成できる
rule(
t1: simple(:x),
t2: sequence(:y)
) {
puts ('match simple t1 and sequence h2')
p x
p y
}
end
TransformTest.new.apply({ k1: 'aaa' })
# => match simple
# "aaa"
TransformTest.new.apply({ k1: ['a1', 'a2', 'a3'] })
# => match sequence
# ["a1", "a2", "a3"]
TransformTest.new.apply({ k2: { inner_k: 'hoge'} })
# => match subtree
# {:inner_k=>"hoge"}
TransformTest.new.apply({ t1: 'aaa', t2: ['b1', 'b2'] })
# => match simple t1 and sequence h2
# "aaa"
# ["b1", "b2"]
再び加減算へ
上記のTransformのルールを使って、先程パースできた加減算の構文解析結果を加減算を行いやすいデータ構造にtransformしていきます。
transformのコツ
このtransformのどのルールに引掛かかるのかでよくハマるので僕がよく試しているパターンとして
- 一つずつルールを追加してみる
- できるだけsimpleにマッチするルールを先に試し切る
- その後残った構造がsequenceかsubtreeかを、そこまでのtransform結果を表示しながら地道にマッチさせていく
という流れがあります。
transform処理
というわけでまずは、numberに対応した数値リテラルに対して to_f してrubyの浮動小数点に変換(transform)してみましょう。
require 'parslet'
class CalcParser < Parslet::Parser
rule(:sign) { match('[-+]') }
rule(:integer) {
(match('[1-9]') >> match('[0-9]').repeat) |
match('[0-9]')
}
rule(:decimal) {
str('.') >> match('[0-9]').repeat(1)
}
rule(:number) {
(sign.maybe >> integer >> decimal.maybe).as(:number) >> space?
}
rule(:exp) { (number.as(:left) >> (exp_op >> number.as(:right)).repeat).as(:exp) }
rule(:exp_op) { match('[+-]').as(:op) >> space? }
rule(:space) { match('\s').repeat(1) }
rule(:space?) { space.maybe }
root(:exp)
end
# 追加したTransformクラス
class CalcTransform < Parslet::Transform
rule(number: simple(:x)) { x.to_f }
end
# まずパースする
parsed = CalcParser.new.parse('1 + 2 - 3')
# パース結果表示
p parsed
# => {:exp=>[{:left=>{:number=>"1"@0}}, {:op=>"+"@2, :right=>{:number=>"2"@4}}, {:op=>"-"@6, :right=>{:number=>"3"@8}}]}
# パース結果をtransformした結果を表示
p CalcTransform.new.apply(parsed)
# => {:exp=>[{:left=>1.0}, {:op=>"+"@2, :right=>2.0}, {:op=>"-"@6, :right=>3.0}]}
ここで、パース結果の
{:exp=>[{:left=>{:number=>"1"@0}}, {:op=>"+"@2, :right=>{:number=>"2"@4}}, {:op=>"-"@6, :right=>{:number=>"3"@8}}]}
が、transformのapplyによって
{:exp=>[{:left=>1.0}, {:op=>"+"@2, :right=>2.0}, {:op=>"-"@6, :right=>3.0}]}
に変換しているのがわかります。
{:number => xxx}の部分がすべて xxx.to_f した結果に変換されていますね。
{:left => 1.0} に関しても leftは必ず何かしらの値になるので、 {left: simple(:x)} も x に変換してしまいましょう。
require 'parslet'
class CalcParser < Parslet::Parser
rule(:sign) { match('[-+]') }
rule(:integer) {
(match('[1-9]') >> match('[0-9]').repeat) |
match('[0-9]')
}
rule(:decimal) {
str('.') >> match('[0-9]').repeat(1)
}
rule(:number) {
(sign.maybe >> integer >> decimal.maybe).as(:number) >> space?
}
rule(:exp) { (number.as(:left) >> (exp_op >> number.as(:right)).repeat).as(:exp) }
rule(:exp_op) { match('[+-]').as(:op) >> space? }
rule(:space) { match('\s').repeat(1) }
rule(:space?) { space.maybe }
root(:exp)
end
class CalcTransform < Parslet::Transform
rule(number: simple(:x)) { x.to_f }
# left: xxxの構造も xxxに変換する
rule(left: simple(:x)) { x }
end
parsed = CalcParser.new.parse('1 + 2 - 3')
p parsed
# => {:exp=>[{:left=>{:number=>"1"@0}}, {:op=>"+"@2, :right=>{:number=>"2"@4}}, {:op=>"-"@6, :right=>{:number=>"3"@8}}]}
p CalcTransform.new.apply(parsed)
# => {:exp=>[1.0, {:op=>"+"@2, :right=>2.0}, {:op=>"-"@6, :right=>3.0}]}
さて、次に演算子を結合順序(左結合)に従って木構造を作っていきましょう。
木構造を表すデータ構造は何でもいいのですが、Parsletのサンプルでよく出てくるstructで定義してみます。
BinOpNode = Struct.new(:left, :op, :right)
このBinOpNodeクラスを使って、先程の 1 + 2 - 3 で言えば
BinOpNode.new(
BinOpNode.new(
1.0,
:+,
2.0
),
:-,
3
)
という構造を作ることができれば結合順序も保ったまま加減算が表現できそうです。
さて、もう一度transform結果を見ると
{:exp=>[1.0, {:op=>"+"@2, :right=>2.0}, {:op=>"-"@6, :right=>3.0}]}
となっているので、
-
:exps => subtree(:tree)でマッチさせて、 - treeの先頭に
数値が来て、その後に{:op => 演算子, :right=>数値}の組が0個以上来る
という構造を処理できれば良さそうです。
ただし、注意として、演算子がなく、数値だけの場合(2 とかの場合) 数値が一つだけ入った長さ1の配列ではなく、数値そのものが来ます。
例)
'1'をパースした場合はexpが配列でなく、数値自身が設定される
parsed = CalcParser.new.parse('1')
p parsed
# => {:exp=>{:left=>{:number=>"1"@0}}}
p CalcTransform.new.apply(parsed)
# => {:exp=>1.0}
# {:exp=>[1.0]}ではない
以上を考慮すると、expsに対応するtreeが
- 配列なら、演算子あり、なのでBinOpに畳み込む
- 配列でないなら、tree自身を返す
ができれば良さそうです。
require 'parslet'
class CalcParser < Parslet::Parser
rule(:sign) { match('[-+]') }
rule(:integer) {
(match('[1-9]') >> match('[0-9]').repeat) |
match('[0-9]')
}
rule(:decimal) {
str('.') >> match('[0-9]').repeat(1)
}
rule(:number) {
(sign.maybe >> integer >> decimal.maybe).as(:number) >> space?
}
rule(:exp) { (number.as(:left) >> (exp_op >> number.as(:right)).repeat).as(:exp) }
rule(:exp_op) { match('[+-]').as(:op) >> space? }
rule(:space) { match('\s').repeat(1) }
rule(:space?) { space.maybe }
root(:exp)
end
# 二項演算用クラス
BinOpNode = Struct.new(:left, :op, :right)
class CalcTransform < Parslet::Transform
rule(number: simple(:x)) { x.to_f }
# left: xxxの構造も xxxに変換する
rule(left: simple(:x)) { x }
rule(exp: subtree(:tree)) {
if tree.is_a?(Array)
# 配列ならBinOpNodeに変換
tree.inject do |left, op_right|
# 演算子と右辺を取り出し
op = op_right[:op]
right = op_right[:right]
BinOpNode.new(left, op, right)
end
else
# 配列でないならそのものを返す
tree
end
}
end
parsed = CalcParser.new.parse('1 + 2 - 3')
p parsed
# => {:exp=>[{:left=>{:number=>"1"@0}}, {:op=>"+"@2, :right=>{:number=>"2"@4}}, {:op=>"-"@6, :right=>{:number=>"3"@8}}]}
p CalcTransform.new.apply(parsed)
# => #<struct BinOpNode left=#<struct BinOpNode left=1.0, op="+"@2, right=2.0>, op="-"@6, right=3.0>
きちんとBinOpNodeの入れ子構造に変換できました。
なお、 2 など演算子なしで渡された場合は
parsed = CalcParser.new.parse('2')
p parsed
# => {:exp=>{:left=>{:number=>"2"@0}}}
p CalcTransform.new.apply(parsed)
# => 2.0
となります。
Transform結果の評価
これで生の文字列から、パースして、transformすることで独自のruby上のデータ構造にまで変換することができました。
このデータ構造をよく抽象構文木(=以下AST)と呼ぶので、以降そう記述します。
さて、このAST自体は何も結果を返してくれていません。なので、このASTを元に実際に加減算を行ってみます。
ASTの各末端の要素(数値、だったりBinOpNodeだったり)それぞれに評価処理があると煩雑なので、各処理に対して eval でそれぞれのノードに対応した計算処理がされるようにしてみましょう。
これに伴って、 {number: 数値} でto_fで数値に変換していたところも一旦NumericNodeという数値用のNodeを作成し、それをevalすることで数値を返すようにします。
# 数値用クラス
NumericNode = Struct.new(:value) do
def eval
value.to_f
end
end
# 二項演算用クラス
BinOpNode = Struct.new(:left, :op, :right) do
def eval
l = left.eval
r = right.eval
case op
when '-'
l - r
when '+'
l + r
else
raise "予期しない演算子です. #{op}"
end
end
end
これを元にtransformまで考慮し、transformの結果を評価(eval)するところまで含めると下記のようになります。
require 'parslet'
class CalcParser < Parslet::Parser
rule(:sign) { match('[-+]') }
rule(:integer) {
(match('[1-9]') >> match('[0-9]').repeat) |
match('[0-9]')
}
rule(:decimal) {
str('.') >> match('[0-9]').repeat(1)
}
rule(:number) {
(sign.maybe >> integer >> decimal.maybe).as(:number) >> space?
}
rule(:exp) { (number.as(:left) >> (exp_op >> number.as(:right)).repeat).as(:exp) }
rule(:exp_op) { match('[+-]').as(:op) >> space? }
rule(:space) { match('\s').repeat(1) }
rule(:space?) { space.maybe }
root(:exp)
end
# 数値用クラス
NumericNode = Struct.new(:value) do
def eval
value.to_f
end
end
# 二項演算用クラス
BinOpNode = Struct.new(:left, :op, :right) do
def eval
l = left.eval
r = right.eval
case op
when '-'
l - r
when '+'
l + r
else
raise "予期しない演算子です. #{op}"
end
end
end
class CalcTransform < Parslet::Transform
rule(number: simple(:x)) { NumericNode.new(x) }
# left: xxxの構造も xxxに変換する
rule(left: simple(:x)) { x }
rule(exp: subtree(:tree)) {
if tree.is_a?(Array)
# 配列ならBinOpNodeに変換
tree.inject do |left, op_right|
# 演算子と右辺を取り出し
op = op_right[:op]
right = op_right[:right]
BinOpNode.new(left, op, right)
end
else
# 配列でないならそのものを返す
tree
end
}
end
parsed = CalcParser.new.parse('1 - 2 + 3')
p parsed
# => {:exp=>[{:left=>{:number=>"1"@0}}, {:op=>"-"@2, :right=>{:number=>"2"@4}}, {:op=>"+"@6, :right=>{:number=>"3"@8}}]}
ast = CalcTransform.new.apply(parsed)
p ast
# => #<struct BinOpNode left=#<struct BinOpNode left=#<struct NumericNode value="1"@0>, op="-"@2, right=#<struct NumericNode value="2"@4>>, op="+"@6, right=#<struct NumericNode value="3"@8>>
p ast.eval
# => 2.0
最後の出力からわかるように
p ast.eval
# => 2.0
ということで、生文字列 => AST => ASTの評価 => 加減算の結果
にできましたね!
その3に続く