Typst で三次元空間に図形を描画する [CeTZ]

この記事は TSG Advent Calendar 2024 の4日目の記事です。3日遅れてすみませんでした！

はじめに

Typst とは、マークアップベースの組版システム・文書作成ツールです。
文書作成ツールと言えば、特に数式組版の文脈では LaTeX が非常に有名ですが、Typst は LaTeX と同等の機能性を、よりモダンなシステム・インターフェースで提供することを目標にしています。
LaTeX と同様に、Typst は様々なパッケージによって機能を付加することができますが、今回は Typst の描画パッケージの一つである CeTZ の三次元空間上での描画機能を紹介します。

本記事は、執筆時点で最新バージョンの CeTZ 0.3.1 をベースに書かれています。

本記事のコードを含めて、Typst コードは Typst ウェブ版（要ユーザー登録） でブラウザ上で試すことができます。

三次元空間のセットアップ

素の Typst にも、基本的な図形描画機能は備わっています。円・折れ線・矩形などを描画する関数が用意されており、簡易的な図を作るにはこれで十分でしょう。

一方で、複雑な図形の描画や、ましてや三次元図形の描画を Typst 標準の関数のみで実装するのは面倒です。そんなときには、CeTZ という描画パッケージが便利です。CeTZ は以下の一行を追加することでインポートすることができます。

#import "@preview/cetz:0.3.1"

これで CeTZ ライブラリの関数を #cetz. を先頭につけることで呼び出すことができます。

特に #cetz.draw. 以下の関数を呼び出すことが頻繁にあるので、各 CeTZ コード片の先頭に

import cetz.draw: *

とすると、そのコード片の中では #cetz.draw. を書かずとも関数を呼べるようになります。

CeTZ ライブラリ上での三次元座標 $(x, y, z)$ は、サイズ $4 \times 4$ の行列 $T$ によって定められる変換で紙面の二次元座標に転写されます。具体的には、座標 $(x,y,z)$ を指定した時、以下の式

(x', y', z',1)^\top = T(x,y,z,1)^\top

で定められる $x', y'$ によって、紙面上では $(x',y')$ に表示されます。デフォルトの $T$ は

T=\begin{pmatrix}
1&0&-0.5&0\\
0&-1&0.5&0\\
0&0&1&0\\
0&0&0&1\\
\end{pmatrix}

に設定されているため、$x$ 軸は右方向、$y$ 軸は上方向、$z$ 軸は左下方向を向くようになっています。

$T$ は set-transform 関数によって指定することができるほか、rotate translate scale などの関数で変換することが可能です。
また、正規直交座標系の射影に特化した ortho 関数というヘルパー関数も用意されています。

使用例

例として、以下のコード

let AXIS_LENGTH = 2.5
line((0, 0, 0), (AXIS_LENGTH, 0, 0), mark: (end: ">"), name: "x-axis")
line((0, 0, 0), (0, AXIS_LENGTH, 0), mark: (end: ">"), name: "y-axis")
line((0, 0, 0), (0, 0, AXIS_LENGTH), mark: (end: ">"), name: "z-axis")
content("x-axis.end", [$x$], anchor: "west")
content("y-axis.end", [$y$], anchor: "south")
content("z-axis.end", [$z$], anchor: "north-east")

で、x, y, z 軸を描画してみましょう。

① set-transform

set-transform(((1, 0, -0.2, 0), (0, -1, 0.2, 0), (0, 0, 1, 0), (0, 0, 0, 1)))
<描画コード>

② scale, rotate

set-transform(none) // T を単位行列に初期化
rotate(x: 20deg)
rotate(z: 45deg)
scale(z: 1.5)
<描画コード>

③ ortho

ortho(x: 30deg, y: 45deg, {
  <描画コード>
})

結果

(※描画コードにある anchor パラメータは射影の向きによって微調整しました)

二次元図形の空間上への描画

CeTZ の基本図形の多く（line や rect など）は、座標を受け取る引数にそのまま三次元座標 (大きさ 3 の配列) を与えることで、該当の箇所に図形を書くことができます。特に line 関数は、Typst デフォルトの line 関数と違い、3 つ以上の点を与えて折れ線（close: true を渡すと閉じた折れ線、さらに fill: black などで中身を塗りつぶす）を描けるため、多角形を描画したいときは line が活躍するでしょう。

ここで注意ですが、描画はあくまで二次元上の紙面で行われ、記述順に図形が紙面上に描画されていきます。よって、三次元空間上で図形が交差していたとしても、CeTZ がその交差を考慮して描画することはありません。
現状、三次元空間中の図形の交差を忠実に描画したい場合には、手動での描画が必要になります。

grid など、一部図形は（現バージョンでは）三次元座標のサポートがされていません。
そのような図形でも、on-xy on-xz on-yz 環境の中で描画することで、指定する切片上の xy, yz, xz 平面に描画することができます。

例

#import "@preview/cetz:0.3.1"

#cetz.canvas({
  import cetz.draw: *
  let AXIS_LENGTH = 5.5
  ortho(x: 20deg, y: 20deg, {
    line((0, 0, 0), (0, 0, AXIS_LENGTH), mark: (end: ">"))
    line((0, 0, 0), (0, AXIS_LENGTH, 0), mark: (end: ">"))
    line((0, 0, 0), (AXIS_LENGTH, 0, 0), mark: (end: ">"))
    on-xz({
      grid((0, 0), (5.5, 5.5), step: 1.0, stroke: gray + 0.2pt)
    })
    on-xy({
      grid((0, 0), (5.5, 5.5), step: 1.0, stroke: gray + 0.2pt)
    })
    on-yz({
      grid((0, 0), (5.5, 5.5), step: 1.0, stroke: gray + 0.2pt)
    })

    let L = 4
    // 交差部分を赤く描画
    line((0, 0, L), (L/2, L/2, L/2), (0, L, 0), close:true, fill: red.transparentize(20%), stroke: 0pt)
    line((0, L, 0), (L/2, L/2, L/2), (L, 0, 0), close:true, fill: red.transparentize(20%), stroke: 0pt)
    line((L, 0, 0), (L/2, L/2, L/2), (0, 0, L), close:true, fill: red.transparentize(20%), stroke: 0pt)
    line((0, 0, L), (L, L, 0), stroke: 0.2pt)
    line((0, L, 0), (L, 0, L), stroke: 0.2pt)
    line((L, 0, 0), (0, L, L), stroke: 0.2pt)
    
    // 空間中に長方形を描画
    line((0, 0, L), (0, L, 0), (L, L, 0),  (L, 0, L), close:true, fill:blue.transparentize(80%), stroke: 0.2pt)
    line((0, L, 0), (L, 0, 0), (L, 0, L),  (0, L, L), close:true, fill:blue.transparentize(80%), stroke: 0.2pt)
    line((L, 0, 0), (0, 0, L), (0, L, L),  (L, L, 0), close:true, fill:blue.transparentize(80%), stroke: 0.2pt)
  })
})

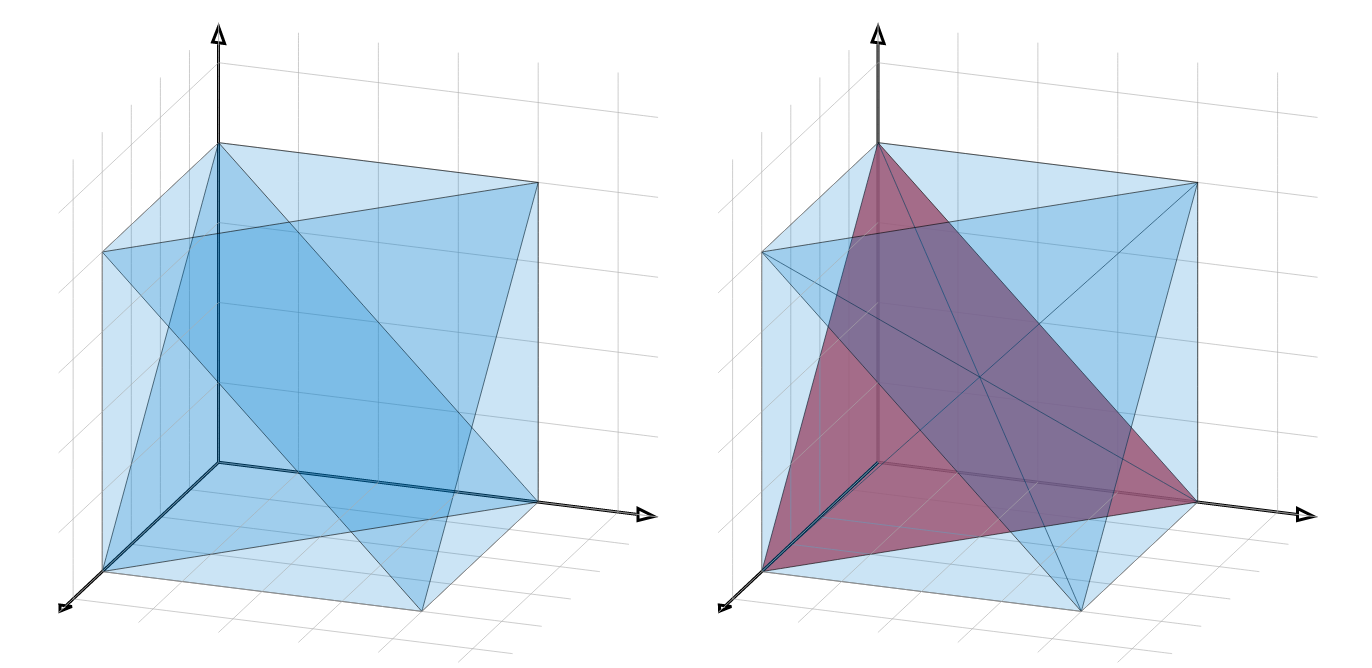
結果

上のコードで「交差部分を赤く描画」以下 6 行をコメントアウトすると左側の図に、しないと右側の図になります。

複雑な図形の描画

Typst には強力なスクリプト機能が備わっており、変数・配列を用いた演算、if 文による条件分岐、for, while 文によるループがサポートされています。
（実は、上に登場したコード例でも、軸の大きさ AXIS_LENGTH や長方形の短辺の大きさ L など、一部のパラメータが変数として実装されているため、値の変更によって図の内容が変わる仕組みになっています。）

Typst のスクリプト機能と CeTZ パッケージのレンダリング機能を組み合わせて、変数の中身によって図の内容が変わる自作関数を定義することができます。

多面体の描画

以下の polyhedron 関数に三次元座標（大きさ 3 の配列）の配列 vertices と面を構成する頂点の番号 faceIndexes を与えると、多面体を描画します。オプション引数で stroke (辺の見た目) と fill (面の見た目) を指定できます。

#let polyhedron(vertices, faceIndexes, ..style) = {
  import cetz.draw: *
  for face in faceIndexes {
    line(..face.map(i => {
      assert(0 <= i and i < vertices.len(), message: "Vertex index out of bounds"); 
      vertices.at(i)
    }), 
    close: true, 
    stroke: style.at("stroke", default: 1pt), 
    fill: style.at("fill", default: blue))
  }
}

使用例

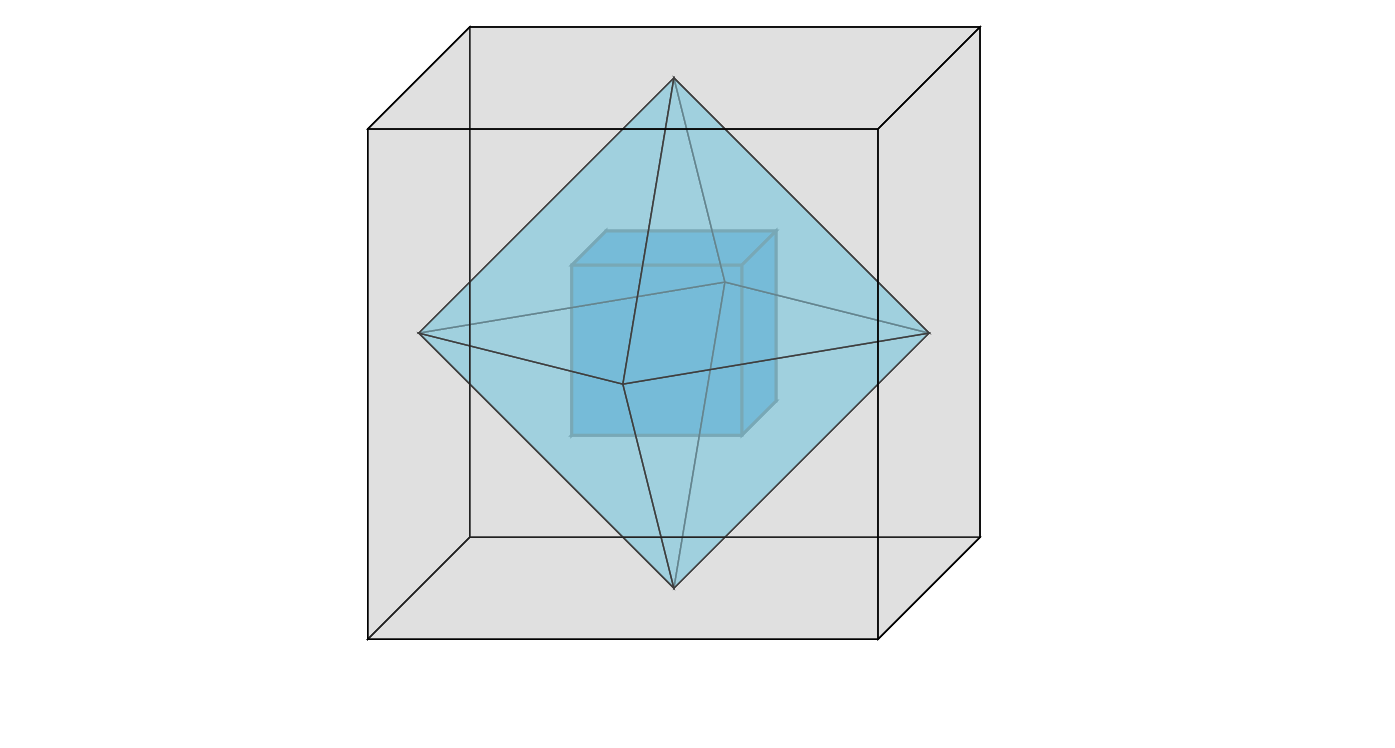
立方体の中に正八面体、そのなかに立方体を描画しています。

#cetz.canvas({
  import cetz.draw: *
  
  set-transform(((1, 0, -0.2, 0), (0, -1, 0.2, 0), (0, 0, 1, 0), (0, 0, 0, 1)))

  let cube(size, ..style) = {
    polyhedron(((-size, -size, -size), (-size, -size, size), (-size, size, -size), (-size, size, size), (size, -size, -size), (size, -size, size), (size, size, -size), (size, size, size)), ((0, 1, 3, 2), (0, 1, 5, 4), (0, 2, 6, 4), (1, 3, 7, 5), (2, 6, 7, 3), (4, 5, 7, 6)), stroke: style.at("stroke"), fill: style.at("fill"))
  }

  let octahedron(size, ..style) = {
    polyhedron(((-size, 0, 0), (size, 0, 0), (0, -size, 0), (0, size, 0), (0, 0, -size), (0, 0, size)), ((0, 2, 4), (0, 2, 5), (0, 3, 4), (0, 3, 5), (1, 2, 4), (1, 2, 5), (1, 3, 4), (1, 3, 5)), stroke: style.at("stroke"), fill: style.at("fill"))
  }

  cube(1, stroke: 1pt, fill: blue)
  octahedron(3, stroke: 0.5pt, fill: aqua.transparentize(50%))
  cube(3, stroke: 0.5pt, fill: gray.transparentize(80%))
})

結果

三次元グラフ $z = f(x,y)$ の描画

以下の graph-3d 関数に 2 引数関数 f を与えると、三次元グラフ（$z = f(x, y)$ を満たす $(x,y,z)$）を描画します。オプション引数 xrange yrange tick で値域とサンプル幅、stroke で線の見た目を変更できます。

#let graph-3d(f, xrange: (0, 1), yrange: (0, 1), tick: 0.1, ..style) = {
  import cetz.draw: *
  let (x-tick, y-tick) = if type(tick) == array {tick} else {(tick, tick)}
  assert(x-tick > 0 and y-tick > 0, message: "Tick must be positive")
  for xi in range(int((xrange.at(1) - xrange.at(0)) / x-tick) + 1) {
    let x = (xi * x-tick) + xrange.at(0)
    line(..(for yi in range(int((yrange.at(1) - yrange.at(0)) / y-tick) + 1){
      let y = (yi * y-tick) + yrange.at(0)
      ((x, y, f(x, y)),)
    }), stroke: style.at("stroke", default: 0.2pt + gray))
  }
  for yi in range(int((yrange.at(1) - yrange.at(0)) / y-tick) + 1) {
    let y = (yi * y-tick) + yrange.at(0)
    line(..(for xi in range(int((xrange.at(1) - xrange.at(0)) / x-tick) + 1){
      let x = (xi * x-tick) + xrange.at(0)
      ((x, y, f(x, y)),)
    }), stroke: style.at("stroke", default: 0.2pt + gray))
  }
}

使用例

$z = \sin x + \cos y + 2$ を $0 \leq x, y \leq 5$（サンプル幅 $0.1$）の範囲で描画します。

#cetz.canvas({
  import cetz.draw: *
  let AXIS_LENGTH = 5;
  
  set-transform(((1, -0.2, 0, 0), (0, 0.2, -1, 0), (0, 1, 0, 0), (0, 0, 0, 1)))
  
  line((0, 0, 0), (AXIS_LENGTH, 0, 0), mark: (end: ">"), name: "x-axis")
  line((0, 0, 0), (0, AXIS_LENGTH, 0), mark: (end: ">"), name: "y-axis")
  line((0, 0, 0), (0, 0, AXIS_LENGTH), mark: (end: ">"), name: "z-axis")
  content("x-axis.end", [$x$], anchor: "west")
  content("y-axis.end", [$y$], anchor: "north-east")
  content("z-axis.end", [$z$], anchor: "south")

  line((0, 0, 0), (0, 0, AXIS_LENGTH), mark: (end: ">"))
  line((0, 0, 0), (0, AXIS_LENGTH, 0), mark: (end: ">"))
  line((0, 0, 0), (AXIS_LENGTH, 0, 0), mark: (end: ">"))
  
  on-xz({
    grid((0, 0), (AXIS_LENGTH, AXIS_LENGTH), step: 1.0, stroke: gray + 0.2pt)
  })
  on-xy({
    grid((0, 0), (AXIS_LENGTH, AXIS_LENGTH), step: 1.0, stroke: gray + 0.2pt)
  })
  on-yz({
    grid((0, 0), (AXIS_LENGTH, AXIS_LENGTH), step: 1.0, stroke: gray + 0.2pt)
  })

  graph-3d(
    (x, y) => calc.sin(x) + calc.cos(y) + 2, 
    xrange: (0, AXIS_LENGTH), yrange: (0, AXIS_LENGTH), 
    tick: 0.2, stroke: 0.5pt + orange)
})

結果

おわりに

Typst を使うとき、CeTZ は 3 次元の図を描画するのにとても便利なパッケージです。
皆さんもちょっとした 3 次元図形を PDF 中に忍ばせたいときは CeTZ を使ってみてはいかがでしょうか。