LoginSignup
4
1

More than 5 years have passed since last update.

@pizyumi(ゆりな🎀)

プログラマー向けの（？）数理論理学（４）証明図

Last updated at Posted at 2018-11-12

プログラマー向けというか、数理論理学の枠組みをプログラムとして実装したい人とか形式化数学をやりたい人向けの記事かもしれません（形式化数学についてはこちらの記事もどうぞ）。

なお、ソースコード全体はGitHubにあります。

https://github.com/pizyumi/rena

連載まとめ

証明図

ここまで数学的言明に対する証明を行うための数理論理学の枠組みとプログラムにおける実装について見てきました。

そして、現時点で含意のみに関する数学的言明の多くは証明できるようになっています（実は現時点ではまだ含意のみに関する数学的言明が全て証明できる訳ではないです）。

これから含意以外を含む数学的言明も証明できるようにしていかなければなりませんが、その前に1つやっておきたいことがあります。

それが証明図です。

証明図とは証明の内容を図として表したものです。

今まで作成してきたプログラムにおいて証明は下のように表現されていました。

[1]P1
[2]P2
[3]P3
[4]( P2 → P3 )
[5]( P1 → ( P2 → P3 ) )
[6]( P1 → ( P2 → P3 ) ) |- ( P1 → ( P2 → P3 ) )
[7]P1 |- P1
[8]P1, ( P1 → ( P2 → P3 ) ) |- ( P2 → P3 )
[9]P2 |- P2
[10]P2, P1, ( P1 → ( P2 → P3 ) ) |- P3
[11]P2, ( P1 → ( P2 → P3 ) ) |- ( P1 → P3 )
[12]( P1 → ( P2 → P3 ) ) |- ( P2 → ( P1 → P3 ) )
[13] |- ( ( P1 → ( P2 → P3 ) ) → ( P2 → ( P1 → P3 ) ) )

しかし、この表現は証明の構造が分かりにくいという欠点があります。どのような流れで最後の結論が得られているのか分かりにくいです。

証明図は証明を図的に表示することにより、証明の構造や流れをより分かりやすくします。

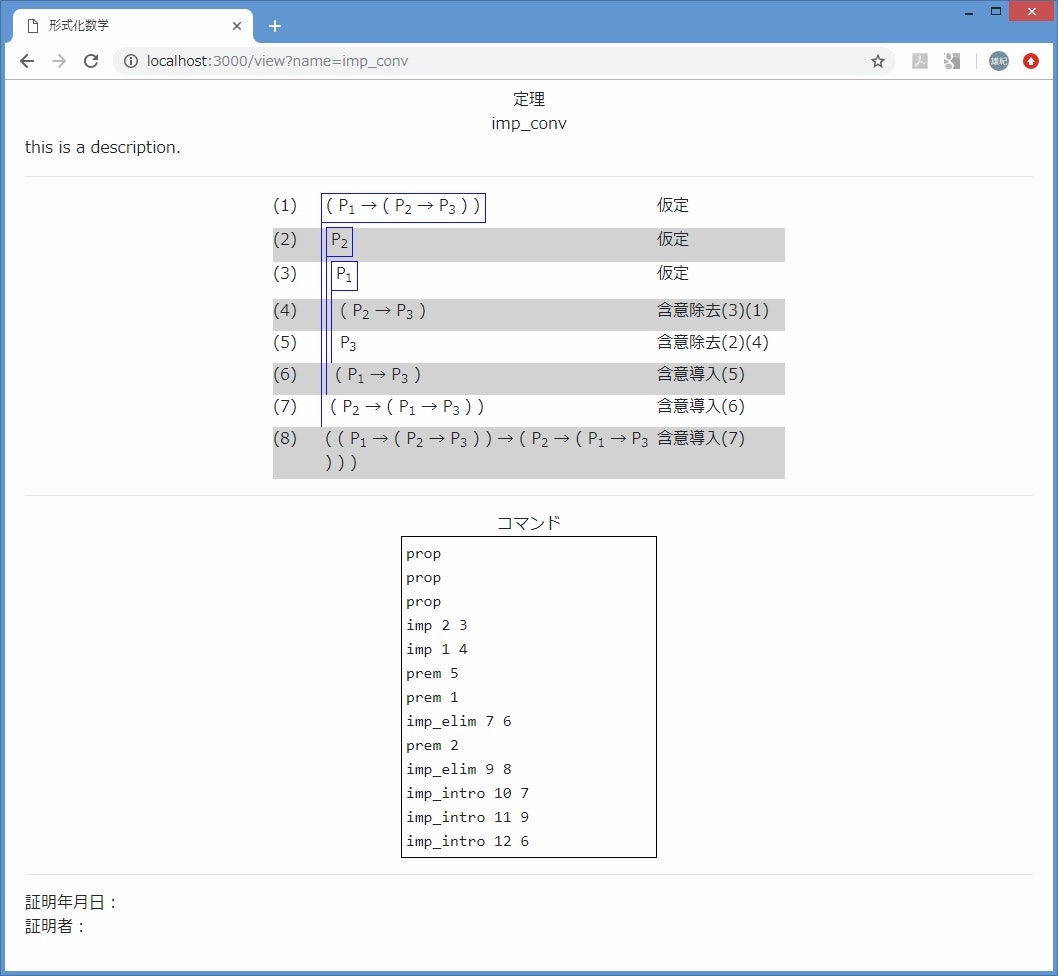
証明図にも幾つかの表現方法の流儀がありますが、今回は下のような証明図を表示する機能を実装したいと思います。

fm08.jpg

なお、上のような形式の証明図をFitch流と言います。

Fitch流の証明図では仮定を線で囲み、その仮定が落ちていない証明のステップには旗を立てるような感じで左端に線を引きます。

これにより、仮定がどこで導入され、どこで落とされたのかが一目瞭然になります。

また、それぞれの証明のステップには番号を付け、推論規則を適用している場合にはどのような推論規則を何に適用しているかを示すことで証明の流れが追い易くなります。

証明図の表示

ここから下は証明図をプログラムでどう実装するかという話なので、プログラミングに興味のない方は飛ばして次の記事に進んでください。

それでは証明図の表示をプログラムで実装しましょう。

証明図を表示するプログラムは現在作成しているウェブアプリの一部となるため、証明図はHTML形式で表示することにします。

そうすると、どのような構造のHTMLによって証明図を作り上げるかが問題となってきますが、たとえば、上の(P1 → (P2 → P3)) → (P2 → (P1 → P3))という言明の証明図は下のような構造のHTMLとして作り上げることにします。

<div class="fitch">
  <div class="box">
    <div class="prem">
      <div class="background-white" style="height: 208px;"></div>
      <div class="index">(1)</div>
      <div class="rule">仮定</div>( P<sub>1</sub> → ( P<sub>2</sub> → P<sub>3</sub> ) )</div>
    <div class="preming">
      <div class="prem">
        <div class="background-black" style="height: 208px;"></div>
        <div class="index">(2)</div>
        <div class="rule">仮定</div>P<sub>2</sub></div>
      <div class="preming">
        <div class="prem">
          <div class="background-white" style="height: 208px;"></div>
          <div class="index">(3)</div>
          <div class="rule">仮定</div>P<sub>1</sub></div>
        <div class="preming">
          <div class="normal">
            <div class="background-black" style="height: 208px;"></div>
            <div class="index">(4)</div>
            <div class="rule">含意除去(3)(1)</div>( P<sub>2</sub> → P<sub>3</sub> )</div>
          <div class="normal">
            <div class="background-white" style="height: 208px;"></div>
            <div class="index">(5)</div>
            <div class="rule">含意除去(2)(4)</div>P<sub>3</sub></div>
        </div>
        <div class="conc">
          <div class="background-black" style="height: 208px;"></div>
          <div class="index">(6)</div>
          <div class="rule">含意導入(5)</div>( P<sub>1</sub> → P<sub>3</sub> )</div>
      </div>
      <div class="conc">
        <div class="background-white" style="height: 208px;"></div>
        <div class="index">(7)</div>
        <div class="rule">含意導入(6)</div>( P<sub>2</sub> → ( P<sub>1</sub> → P<sub>3</sub> ) )</div>
    </div>
    <div class="conc">
      <div class="background-black" style="height: 208px;"></div>
      <div class="index">(8)</div>
      <div class="rule">含意導入(7)</div>( ( P<sub>1</sub> → ( P<sub>2</sub> → P<sub>3</sub> ) ) → ( P<sub>2</sub> → ( P<sub>1</sub> → P<sub>3</sub> ) ) )</div>
    <div class="background-white" style="height: 208px;"></div>
  </div>
</div>

証明図のそれぞれのステップはfitchクラスの<div>要素とboxクラスの<div>要素の内側に格納します。

また、仮定を表すステップはpremクラスの<div>要素となり、仮定を落とすステップはconcクラスの<div>要素となり、それ以外はnormalクラスの<div>要素となります。

ステップを表す<div>要素の中には背景色を適用するbackground-whiteクラス又はbackground-blackクラスの<div>要素とステップの番号を表すindexクラスの<div>要素とステップの種類を表すruleクラスの<div>要素を格納します。background-whiteクラスとbackground-blackクラスの<div>要素は交互に使用します。

ただし、1つ注意しなければならないのは仮定を置いてから仮定を落とすまでの1個以上のステップは纏めて1つのpremingクラスの<div>要素に格納しなければならないということです。

そのため、複数の仮定がまだ落ちていないで残っているステップは入れ子状になったpremingクラスの<div>要素の中に格納されることになります。

そして、このような構造のHTMLに適切なCSSを適用することによって適切な外観の証明図として表示されるようにします。

CSSは下のようになります。

div.fitch {
    width: 768px;
    margin: auto;
}

div.box {
    margin-left: 48px;
    margin-right: 128px;
    position: relative;
}

div.prem {
    border: solid 1px blue;
    display: inline-block;
    padding: 0px 4px 4px 4px;
}

div.preming {
    border-left: solid 1px blue;
    padding: 4px;
}

div.normal {
    padding: 4px;
}

div.conc {
    padding: 0px 4px 4px 4px;
}

div.index {
    position: absolute;
    left: -48px;
    width: 48px;
}

div.rule {
    position: absolute;
    left: 528px;
    width: 192px;
}

div.background-black {
    position: absolute;
    left: -48px;
    width: 768px;
    background-color: lightgrey;
    z-index: -1;
    height: 2048px;
}

div.background-white {
    position: absolute;
    left: -48px;
    width: 768px;
    background-color: white;
    z-index: -1;
    height: 2048px;
}

そして、上のようなHTML形式の証明図を作成するtofitchhtml関数は下のようになります。

引数として証明を表すオブジェクトを取ります。

tofitchhtml関数の中で最初に呼び出しているtofitchorder関数で適切な並びの証明のステップを作り上げる作業を行っています。証明のそれぞれのステップはそのステップまでの証明を表すオブジェクトとなります。

tofitchorder関数には第1引数として証明を表すオブジェクトを渡し、第2引数と第3引数には空の配列を渡すようにします。

すると、第3引数として渡した配列に証明のそれぞれのステップが順番に格納されます。

それぞれの証明のステップに番号を付け、証明のステップの種類に従って適切な<div>要素を作成し、適切な親要素に格納します。

なお、ruleクラスの<div>要素には使用した推論規則の詳細を表示しますが、推論規則の適用において証明のどのステップを使用しているかやどの仮定を落としているかなども表示しています（[、]で囲まれている番号が仮定に付与されている番号を表しています）。

そして、最終的に出来上がったHTMLを返り値として返します。

1つ注意しなければならない点は仮定が落ちない含意導入規則の適用がある場合、その時に導入される仮定は証明図のステップとしては扱わないということです。

たとえば、命題Pを仮定して命題Qが得られ、そこから含意導入規則を適用して命題P → Qを導き出す際には仮定Pが落ちるため証明図に仮定Pが証明のステップとして表示されます。しかし、命題Pを仮定しないで命題Qが得られ、そこから含意導入規則を適用して命題P → Qを導き出す際には仮定Pが落ちないため証明図には仮定Pが表示されることはありませんので注意してください。

そして、仮定が落ちないかどうかをチェックするためにcontainpremise関数を実装し、使用しています。

function tofitchhtml (pr) {
    var ps = [];
    var steps = [];

    tofitchorder(pr, ps, steps);

    var num = 0;
    var prs = [];
    for (var i = 0; i < steps.length; i++) {
        num++;

        steps[i].num = num;
        prs.push(steps[i]);
    }

  var fitch = $('<div class="fitch"></div>');
  var box = $('<div class="box"></div>');

  fitch.append(box);

  var parent = box;
    for (var i = 0; i < prs.length; i++) {
    if (prs[i].subtype === 'imp_intro' && containpremise(prs[i].sub1, prs[i].sub2)) {
      var temp = parent;

      parent = parent.parent();

            if (temp.children().length === 0) {
                temp.remove();
            }
        }

    var cname = '';
    var rname = ''
    if (prs[i].subtype === 'prem') {
      cname = 'prem';
      rname = '仮定' + '[' + prs[i].dindex + ']';
    }
    else if (prs[i].subtype === 'imp_elim') {
      cname = 'normal';
      rname = '含意除去(' + prs[i].sub1.num + ')' + '(' + prs[i].sub2.num + ')';
    }
    else if (prs[i].subtype === 'imp_intro') {
      if (containpremise(prs[i].sub1, prs[i].sub2)) {
        cname = 'conc';
        rname = '含意導入(' + prs[i].sub2.num + ')-(' + prs[i].sub1.num + ')' + '[' + prs[i].sub2.dindex + ']';
      }
      else {
        cname = 'normal';
        rname = '含意導入(' + prs[i].sub1.num + ')' + '[' + prs[i].sub2.dindex + ']';
      }
    }
    else {
      throw new Error('not supported subtype.');
    }

    var line = $('<div class="' + cname + '"></div>');
    var background = $('<div class="' + (i % 2 === 0 ? 'background-white' : 'background-black') + '"></div>');
    var index = $('<div class="index">(' + (i + 1) + ')</div>');
    var rule = $('<div class="rule">' + rname + '</div>');

    line.html(tohtml(prs[i].conclusion));
    line.prepend(rule);
    line.prepend(index);
    line.prepend(background);

    parent.append(line);

        if (prs[i].subtype === 'prem') {
      var preming = $('<div class="preming"></div>');

      parent.append(preming);
      parent = preming;
        }
    }

  var last = $('<div class="background-white"></div>');

  box.append(last);

  return fitch.prop('outerHTML');
}

function tofitchorder (pr, ps, steps) {
  if (pr.type !== 'proof') {
    throw new Error('not proof.');
  }

  if (pr.subtype === 'imp_elim') {
    var f = true;
    for (var i = 0; i < ps.length; i++) {
      if (equal(pr, ps[i])) {
        f = false;
        break;
      }
    }

    if (f) {
      tofitchorder(pr.sub1, ps, steps);
      tofitchorder(pr.sub2, ps, steps);

      ps.push(pr);
      steps.push(pr);
    }
  }
  else if (pr.subtype === 'prem') {
    return;
  }
  else if (pr.subtype === 'imp_intro') {
   if (containpremise(pr.sub1, pr.sub2)) {
     steps.push(pr.sub2);
   }

    var ps2 = [];
    for (var i = 0; i < ps.length; i++) {
      ps2.push(ps[i]);
    }
    ps2.push(pr.sub2);

    tofitchorder(pr.sub1, ps2, steps);

    ps.push(pr);
    steps.push(pr);
  }
}

function containpremise (pr, prem) {
  if (pr.type !== 'proof') {
    throw new Error('not proof.');
  }
  if (prem.subtype !== 'prem') {
    throw new Error('not prem.');
  }

  for (var i = 0; i < pr.premises.length; i++) {
    if (equal(pr.premises[i], prem.conclusion)) {
      return true;
    }
  }
  return false;
}

これで証明図を表すHTMLが作成できるようになりました。

定理閲覧ページ

証明図を表すHTMLが作成できるようになったので、これをどこかで見れるようにしたいです。

そこで、下のような、証明した定理の内容を閲覧するためのページを追加しましょう。このページで定理の証明図も見れるようにするという訳です。

fm09.jpg

math.js

上の証明図を作成するコード（tofitchhtml関数とtofitchorder関数）をmath.jsに追加します。

app.js

app.jsのExpressアプリケーションに下のようなルートを追加します。/viewというURLにおいて定理閲覧ページを返すだけのコードです。

      app.get('/view', (req, res, next) => {
        co(function* () {
          var p = path.join('front', 'view.html');
          yield common.send_res_with_html_from_path(res, p);
        }).catch(next);
      });

view.html

下のようなview.htmlを追加します。これが定理閲覧ページのHTMLとなります。上で示した、証明図を表すHTMLに対するCSSも含まれています。

<!DOCTYPE html>
<html lang="ja">
<head>
  <meta charset="utf-8">
  <meta name="viewport" content="width=device-width, initial-scale=1, shrink-to-fit=no">
  <title>形式化数学</title>
  <link rel="stylesheet" href="/asset/lib/bootstrap-4.0.0/css/bootstrap.min.css">
  <style>
body {
    font-family: 'メイリオ';
    width: 1024px;
    margin: auto;
    padding: 8px;
}

pre {
  font-size: 16px;
  margin: 0px;
}

#type {
  text-align: center;
}

#name {
  text-align: center;
}

#commands_header {
  text-align: center;
}

#commands {
  width: 256px;
  margin: auto;
  border: solid 1px black;
  padding: 4px;
}

div.fitch {
    width: 768px;
    margin: auto;
}

div.box {
    margin-left: 48px;
    margin-right: 128px;
    position: relative;
}

div.prem {
    border: solid 1px blue;
    display: inline-block;
    padding: 0px 4px 4px 4px;
}

div.preming {
    border-left: solid 1px blue;
    padding: 4px;
}

div.normal {
    padding: 4px;
}

div.conc {
    padding: 0px 4px 4px 4px;
}

div.index {
    position: absolute;
    left: -48px;
    width: 48px;
}

div.rule {
    position: absolute;
    left: 528px;
    width: 192px;
}

div.background-black {
    position: absolute;
    left: -48px;
    width: 768px;
    background-color: lightgrey;
    z-index: -1;
    height: 2048px;
}

div.background-white {
    position: absolute;
    left: -48px;
    width: 768px;
    background-color: white;
    z-index: -1;
    height: 2048px;
}
  </style>
</head>
<body>
  <script src="/asset/lib/jquery-3.2.1/jquery-3.2.1.min.js"></script>
  <script src="/asset/lib/vue-2.5.13/vue.min.js"></script>
  <script src="/asset/lib/axios-0.17.1/axios.min.js"></script>
  <script src="/asset/lib/underscore-1.8.3/underscore-min.js"></script>

  <div id="main" v-show="loaded">
    <div id="type">定理</div>
    <div id="name">{{ name }}</div>
    <div id="description">{{ description }}</div>
    <hr>
    <div id="proof">{{ proof }}</div>
    <hr>
    <div id="commands_header">コマンド</div>
    <div>
      <pre id="commands"></pre>
    </div>
    <hr>
    <div id="date">証明年月日：</div>
    <div id="author">証明者：</div>
  </div>

  <script src="/asset/js/math.js"></script>
  <script src="/asset/js/interface.js"></script>
  <script src="/asset/js/view.js"></script>
</body>
</html>

view.js

下のようなview.jsを追加します。定理閲覧ページに特有のJavaScriptとして定理閲覧ページで読み込まれるものです。

function get_query()
{
    var vars = [], max = 0, hash = "", array = "";
    var url = window.location.search;

    hash  = url.slice(1).split('&');
    max = hash.length;
    for (var i = 0; i < max; i++) {
        array = hash[i].split('=');
        vars.push(array[0]);
        vars[array[0]] = array[1];
    }

    return vars;
}

var query = get_query();
var id = 0;

var context = {};

initialize_context(context);

var vm = new Vue({
  el: '#main',
  data: {
        loaded: false,
    name: '',
    description: '',
        commands: []
  },
  computed: {
  },
  methods:  {
  }
});

if (query.name) {
    axios.get('/load?name=' + query.name, {}).then((res) => {
        vm.name = res.data.name;
        vm.description = res.data.description;

        var commands = res.data.commands;
        for (var i = 0; i < commands.length; i++) {
            try {
                var obj = execute_command(context, commands[i]);
                if (obj != undefined && obj != null) {
                    vm.commands.push(commands[i]);
                }
            }
            catch (err) {
            }
        }

        var prhtml = '';
        try {
            prhtml = tofitchhtml(context.ss.get(context.sindex));
        }
        catch (err) {
            console.log(err);
        }

        $('#commands').text(vm.commands.join('\n').trim());
        $('#proof').html(prhtml);

        var height = 16 * vm.commands.length;

        $('.background-white').css('height', height + 'px');
        $('.background-black').css('height', height + 'px');

        vm.loaded = true;
    }).catch((err) => {
    }).finally(() => {
    });
}
else {
    vm.loaded = true;
}

これで定理閲覧ページが見れるようになりました。

閲覧ボタンの追加

定理閲覧ページを見たい時に毎回定理閲覧ページのURLをブラウザに打ち込まなければならないのは面倒なので、定理の証明作業を行うページから定理閲覧ページに飛べる「閲覧」ボタンを追加することにしましょう。

fm10.jpg

main.html

main.htmlに下のような「閲覧」ボタンを追加します。

      <button class="btn btn-primary" @click="view_theorem">閲覧</button>

main.js

main.jsのVueインスタンスのメソッドとして下のようなメソッドを追加します。

        view_theorem: function () {
            window.location.href = '/view?name=' + this.name;
        },

これで定理の証明作業を行うページに「閲覧」ボタンが追加されます。

今回はここまでとします。次回はここまでで作ったプログラムで証明可能な含意のみに関する主要な定理を紹介したいと思います。

4
1
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
4
1