初心者向けです。numpyの練習問題にはなるかも。
全体ソースコード
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import ArtistAnimation
# ==========パラメーター====================
num_of_birds = 100 # 鳥の数
r_min_c = 0.4 # 近づきたい鳥の範囲の内側
r_max_c = 2.2 # 近づきたい鳥の範囲の外側
r_min_s = 0 # 離れたい鳥の範囲の内側
r_max_s = 0.4 # 離れたい鳥の範囲の外側
r_min_a = 0.4 # 整列したい鳥の範囲の内側
r_max_a = 2.2 # 整列したい鳥の範囲の外側
step = 500 # 試行回数
width = 25 # フィールド正方形の1辺
k1 = 1 # 結合係数
k2 = 25 # 分離係数
k3 = 12 # 整列係数
ts = 25 # 描画スピード
v = 0.12 # 鳥の移動スピード
e = 200 # 反発係数
λ = np.pi / 3 # 鳥の視界の範囲
# ==========座標とベクトルをランダム生成===========
pos = np.random.rand(num_of_birds, 2) * (0.6*width - 0.4*width) + 0.4*width # 初期座標。widthの2/5~3/5の間で出現させたい
vec = np.random.rand(num_of_birds, 2) - 0.5 # 初期ベクトル
# ==================4つの関数====================
# 1.距離行列を作る関数
def DISTANCE() :
global distance # 距離の表であるdistanceはグローバルなオブジェクトとして定義しておく
distance = np.zeros([num_of_birds, num_of_birds]) # 空のndarray配列を(鳥の数)*(鳥の数)で作っておく
for i in range (num_of_birds) :
for j in range (i+1, num_of_birds) :
a = pos[i]
b = pos[j]
dist = np.linalg.norm(b-a)
distance[i, j] = dist
distance += distance.T
# 2.r_minとr_maxの間の範囲内にいる鳥さんたちの重心を教えてくれる関数 ※Center of Gravityで重心なのでCG
def GetCG(id, r_min, r_max) :
d = distance[id]
inRange = np.where((d > r_min) & (d < r_max)) [0]
if len(inRange) == 0 :
cg = pos[id] + ((np.random.rand(2)* 2 - 1) * 0.0002)
return cg # ドーナツ内に誰もいなかったら、自分の座標を返す
else :
cg = np.mean(pos[inRange], axis = 0)
return cg #ドーナツ内にあったら、それらの座標の平均を返す
# 3.r_minとr_maxの間の範囲内かつ視界にいる鳥さんのベクトルの平均を教えてくれる関数
def GetVEC(id, r_min, r_max) :
d = distance[id]
inRange = np.where((d > r_min) & (d < r_max)) [0]
if len(inRange) == 0 :
return 0
else :
passlist = []
for i in range(len(inRange)) :
line_vec = pos[inRange][i] - pos[id] # 自分と相手を結んだ直線のベクトル
θ = np.arctan2(line_vec[1], line_vec[0]) # 自分と相手を結んだ直線のベクトルの角度
φ = np.arctan2(vec[id][1], vec[id][0]) # 自分の現在の進行方向ベクトルの角度
if ((φ-λ) < θ) & (θ < (φ+λ)) :
passlist.append([vec[inRange][i]]) # 視界の範囲内に誰かいたら、その誰かの現在の進行方向ベクトルをpasslistに追加
else :
pass
if len(passlist) == 0 :
return 0
else :
pg = np.mean(passlist, axis = 0)
return pg
# 4.鳥が壁に近づいたら、壁と反対方向に反発させるベクトルを計算する関数
def GetRepulsion(id) :
# 壁との垂直距離
left = pos[id][0] - 0 # 左壁との距離
right = width - pos[id][0] # 右壁との距離
under = pos[id][1] - 0 # 下壁との距離
upper = width - pos[id][1] # 上壁との距離
# 壁との距離が1未満だったら、反対方向に反射させる。ベクトルのデカさは距離の2乗に反比例させて、壁に近ければ近いほど反発力を高める
if (left < 1) :
vec_LEFT = np.array([1,0]) / (left**2)
else :
vec_LEFT = 0
if (right < 1) :
vec_RIGHT = np.array([-1,0]) / (right**2)
else :
vec_RIGHT = 0
if (under < 1) :
vec_UNDER = np.array([0,1]) / (under**2)
else :
vec_UNDER = 0
if (upper < 1) :
vec_UPPER = np.array([0,-1]) / (upper**2)
else :
vec_UPPER = 0
# 4方面それぞれの反発ベクトルを合成
vec_R = vec_LEFT + vec_RIGHT + vec_UNDER + vec_UPPER
return vec_R
# ====================以下メインで動かすところ====================
# まずはArtistanimationの準備
fig = plt.figure() # 描画領域の確保
img_list = [] # パラパラ漫画の1枚1枚を保存する空の容器(list)
p_pos = np.zeros([num_of_birds, 2]) # 一時的に新しい座標を保存しておくための空の容器(ndarray)
p_vec = np.zeros([num_of_birds, 2]) # 一時的に新しいベクトルを保存しておくための空の容器(ndarray)
for n in range(step) : # パラパラ漫画の枚数(step)分回す
DISTANCE() # 距離行列を作成。stepを経るごとに距離座標は更新される
for id in range(num_of_birds) : # 鳥の数(num_of_birds)分回す
# お近づきになりたい鳥さんたちの座標の平均
Cohesion = GetCG(id = id, r_min = r_min_c, r_max = r_max_c) - pos[id]
# 距離をおきたい鳥さんたちの座標の平均
Separation = GetCG(id = id, r_min = r_min_s, r_max = r_max_s) - pos[id]
# 一緒に行動したい鳥さんたちのベクトルの平均
Alignment = GetVEC(id = id, r_min = r_min_a, r_max = r_max_a)
# 壁に対しての反発ベクトル
Repulsion = GetRepulsion(id = id)
# 進むべきベクトルを計算して、絶対値で割って単位ベクトル化
vec_T = vec[id] + k1* Cohesion - k2* Separation + k3* Alignment + e* Repulsion
vec_T /= np.linalg.norm(vec_T)
p_pos[id] = pos[id] + vec_T * v # p_posに新しい座標を保存
p_vec[id] = vec_T # p_vecに新しいベクトルを保存
# pos に p_posを代入して座標更新
pos = p_pos
# vec に p_vec を代入してベクトル更新
vec = p_vec
# x座標、y座標として登録
x = pos[:, 0]
y = pos[:, 1]
img = plt.scatter(x, y, s = 3, c= 'blue', marker= '1')
img_list.append([img])
print("step : ", n) # カウント用
print("finished.") # カウント用
# ArtistAnimation で描画
anim = ArtistAnimation(
fig = fig,
artists = img_list,
interval = ts,
blit = True
)
plt.xlim(0, width) # x軸方向の描画範囲
plt.ylim(0, width) # y軸方向の描画範囲
plt.show()
Boidsって何?
wikipedia先生曰く
ボイド(Boids)は、アメリカのアニメーション・プログラマ、クレイグ・レイノルズが考案・作製した人工生命シミュレーションプログラムらしいです。名称は「鳥もどき(bird-oid)」から。
仰々しく人工生命と言われるとSFっぽさが出ますが、そこまで高度なことをするワケではないです。プログラミングで生物の群れっぽいものがシミュレーションできるぜ!というノリです。具体的には、下のgifみたいなものが出来上がります。
初めて見た人は、おそらく「おお~本物の生物っぽい!」という感想を抱くと思います。でも、Boidsの面白ポイントはそこではありません。本当に凄いのは、一見複雑そうに見える群れの動きを
- 結合(Cohesion)
- 分離(Separation)
- 整列(Alignment)
という3つの単純なルールのみで再現しているところです。つまり、3つの基本原理から演繹的に生物の行動を模倣できます。
全体的な仕組み
Boids は群れ全体をプログラムすることで生まれるものではなく、前述した3ルールを鳥1匹ずつに付与することで、結果的に生まれるものです。
具体的には、鳥1匹ずつに結合ベクトル、分離ベクトル、整列ベクトルを含ませて、進行方向を決定するだけでOK。以下では1匹の鳥に注目して、それぞれのルールをざっくり確認していきます。
結合ベクトル
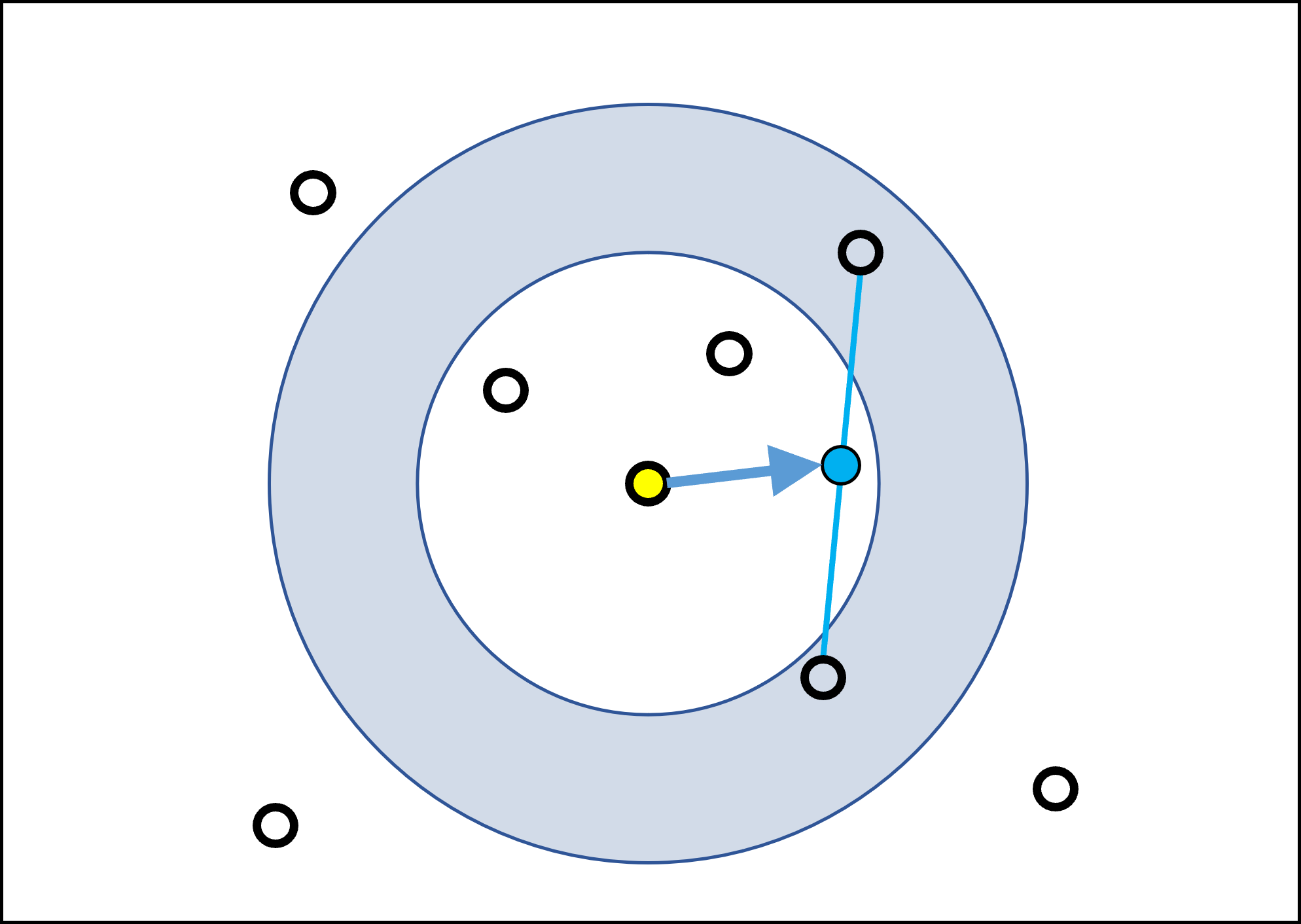
群れるからには、鳥と鳥とが近づかなければいけません。したがって、任意の距離にいる鳥の集団を群れと認識して、その集団に近づいていくようにプログラムすればいいワケです。実際には図のように、ドーナツ領域の中にいる鳥の重心を求め(重心を群れの中心とみなす)、重心に向かって進む方向を接近ベクトルとします。
分離ベクトル

群れだからといって近づきすぎると、鳥と鳥とが衝突してしまいます。そこで、ソーシャルディスタンスを取らせる必要が出てきます。三密回避。原理としては接近ベクトルの真逆。ドーナツ領域の中にいる鳥の重心を求め、それに対して遠ざかる方向を回避ベクトルとします。
整列ベクトル

近づいたり離れたりするだけでは、群れにはなり得ません。周囲の行動に合わせて動く愚かな大衆に仕立て上げる必要があります。ドーナツ領域を考えるまでは接近・回避と同じですが、重心ではなくベクトルの合成を行います。
最終的な進行方向

結合・分離・整列の3つのベクトルを今までの進行方向ベクトルに足し合わせることで、次に進むべきトータルの進行方向ベクトルが得られます。
実際には、鳥が壁にぶつかったときに跳ね返るための反発ベクトルも考慮し、最後に絶対値で割って単位ベクトル化してから用います(つまり純粋に方向だけを表すようにする)。詳細は後ほど。
pythonで鳥をどうやって動かすか
鳥が動き回る様子をどのようにpythonで実装するのかというと、座標(数学で使うようなxy座標)の上に鳥を1匹ずつ”点”としてプロットし、プロットした紙をパラパラ漫画みたく連続でめくってアニメーションにするという手法を用います。
具体的に説明してみます。鳥1匹ずつにそれぞれ
- 現在の場所を表す座標:
pos(x, y) - 進行方向を表すベクトル:
vec(x, y)
の2つを持たせます。
例えば、現在の位置が pos (1, 2) 方向ベクトルが vec (3, 4) だったとしたら、(1+3, 2+4) の計算(場所の座標に方向ベクトルを足す)により、次の座標は (4, 6) に決定されます。このように1回の計算ごとに鳥の座標が少しずつズレていくので、パラパラ漫画にすると鳥が移動しているように見えることになります。
実装
0. 座標と進行方向ベクトル
前項で説明した通り、鳥1匹に対して、「座標」と「進行方向ベクトル」という2つの要素を持たせます。
具体的には、鳥1匹ずつにidで背番号をふり、その番号ごとに
- 座標:
pos[id] - 進行方向ベクトル:
vec[id]
を設定します。以下のコードでは、初期座標と初期ベクトルを一定の範囲内にランダム生成しています。
import numpy as np
width = 25 # フィールド正方形の1辺の長さ。つまりx座標とy座標のとりうる範囲
num_of_birds = 100 # 鳥の数。とりあえず100匹にしておく
pos = np.random.rand(num_of_birds, 2) * (0.6*width - 0.4*width) + 0.4*width # 初期座標をランダム生成する
vec = np.random.rand(num_of_birds, 2) - 0.5 # 初期ベクトルをランダム生成する
posについて詳しく説明します。
まずnp.random.rand()で0.0以上1.0未満の乱数を発生させることができます。
ここでは引数を(num_of_birds, 2)にしているので、ランダムな[x, y]の二次元配列の組がnum_of_birds個、つまり100個生成されたことになります。

このままでは 0 ≦ x < 1, 0 ≦ y < 1 の小さな正方形内に鳥が生成されてしまうので、フィールド中心辺りに生成されるように処理を行わなければなりません。
そこで* (0.6*width - 0.4*width) + 0.4*widthという計算をしています。原理は下の図。
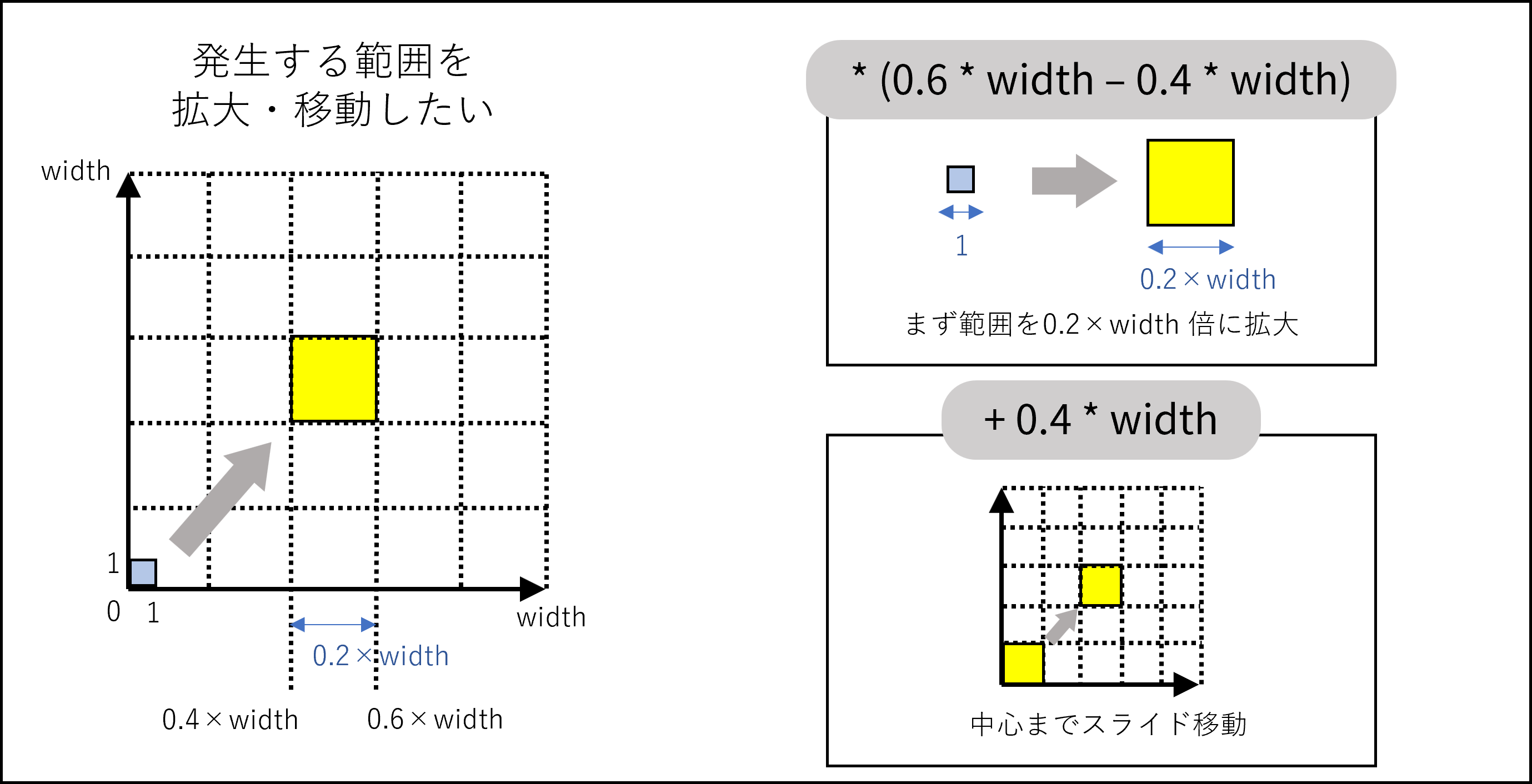
まず 1 × 1 の正方形内の鳥の座標を (0.2 × width) × (0.2 × width) に拡大するために
* (0.6*width - 0.4*width)を行い、
次に正方形をフィールドの中心にスライド移動するために+ 0.4*widthを行っています。
鳥の初期位置を自分でカスタマイズしたければ、ここらへんの数値をいじればOK。
vec の生成もposとほぼ同じだけど、めんどくさいので説明は省略。
1. 距離行列を作る
結合・分離・整列ベクトルを求めるためには、まずは鳥どうしの距離を計算しておく必要があります。先に距離をすべて計算しておくことで、1匹の鳥に対して他の鳥が「近いのか」「遠いのか」を判別することができます。
最初はA~Eの5匹で考えてみます。Aに注目すると、他の鳥との距離は A-B, A-C, A-D, A-E の4種類があり、これはB~Eの鳥に注目したときでも同様です。表にすると下のようになります。

次にA~Eの鳥それぞれに座標を設定してみます。$${A(1, 2) B(3, 4) C(5, 6) D(7, 8) E(9, 10)}$$とすると、例えばA-B間の距離は$${\sqrt{(3-1)^2+(4-2)^2} = 2.8}$$ になります。表に反映させるとこんな感じ。
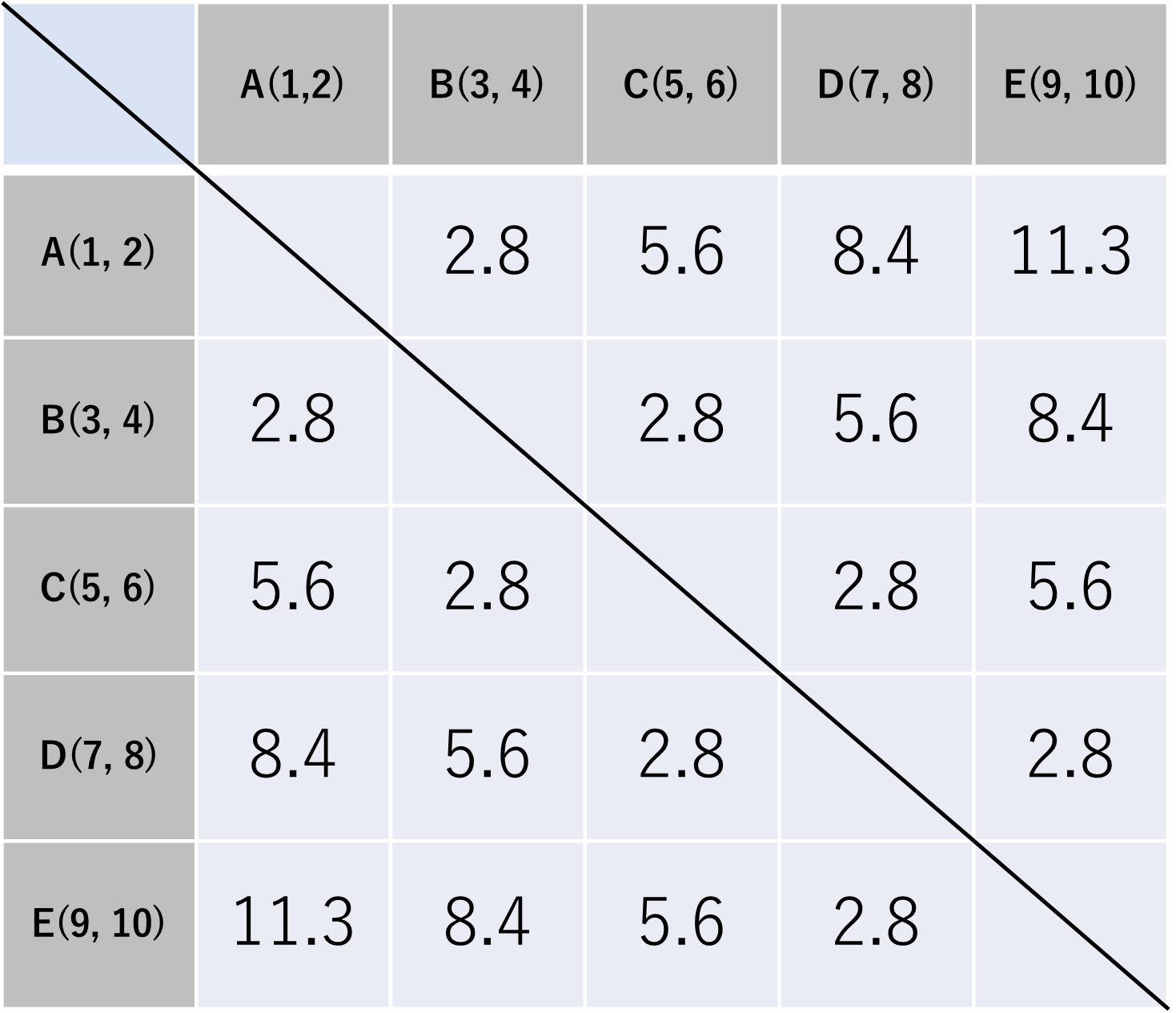
以上で距離行列は完成。
説明を簡単にするために5匹の鳥A~Eに登場してもらいましたが、実際のコーディングでは鳥の位置をposで行います。
距離行列はDISTANCE()という専用の関数で作ることにします。
距離行列そのものは、distanceというグローバル変数に保存します。
def DISTANCE() :
global distance # 距離行列の表であるdistanceはグローバルなオブジェクトとして定義しておく
distance = np.zeros([num_of_birds, num_of_birds]) # 空のndarray配列を(鳥の数)*(鳥の数)で作っておく
for i in range (num_of_birds) :
for j in range (i+1, num_of_birds) :
a = pos[i] # 表の横列
b = pos[j] # 表の縦列
dist = np.linalg.norm(b-a) # 座標間の距離を計算
distance[i, j] = dist # 距離行列の表のマスに代入
distance += distance.T # 表の上半分を反転させて、下半分のマスを埋める
詳しく見ていきます。
まずは、距離行列を保存するdistanceにあらかじめ空の表を作っておきます。
np.zeros()で空のndarray配列を作ることができ、
引数を[num_of_birds, num_of_birds]にすることで、(鳥の数)×(鳥の数)の表が用意されます。
次に、for文2つでiとjを回して、鳥の座標どうしの距離計算を行います。
上のコードでは2匹の鳥の座標をそれぞれaとbでいったん置き換え、
a-b間の距離をnp.linalg()で計算してから表のマスdistance[i, j]に代入しています。
ここまでの計算で、下のような距離行列が出来上がります。
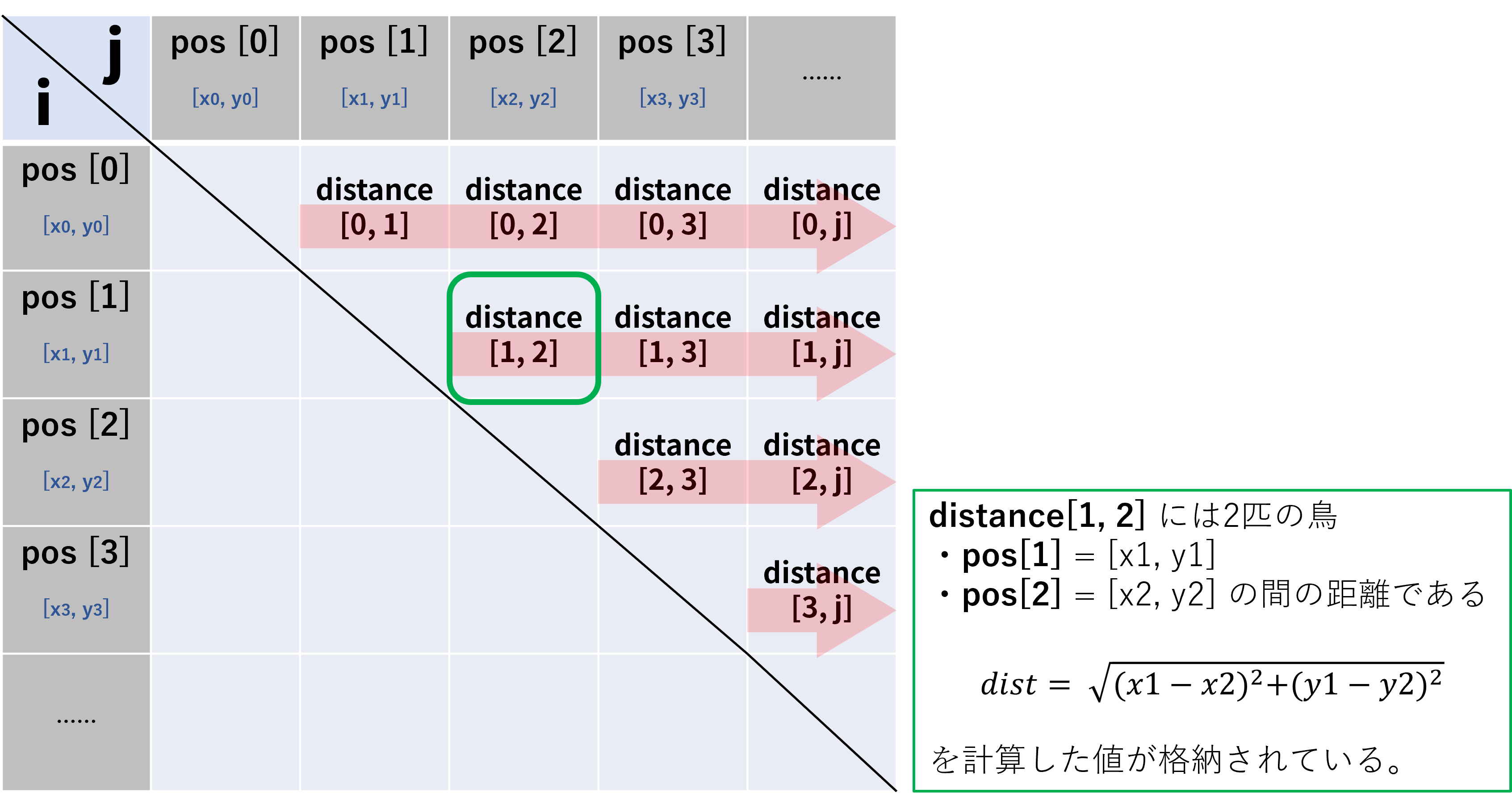
見ての通り、for文2つを回しただけでは表の上半分しか埋まっていません。そこで下半分を埋める処理を行います。
distance += distance.T によって、もともとのdistamce の行と列を入れ替えたdistance.Tが追加されます。
2. 仲間の場所の平均を求める
「全体的な仕組み」の項で記したように、鳥は自分の周囲にドーナツ状の領域を展開して、その領域内にいる仲間に対して近づいたり、あるいは遠ざかったりします。どちらにせよドーナツ状領域を展開して仲間の座標の重心を求めるところまでは同じ処理になるので、
GetCG (id, r_min, r_max)という関数を作りモジュールとして使えるようにしておきます。
引数に指定しているidは鳥1匹ずつに割り振られた背番号、
r_minはドーナツの内径、
r_maxはドーナツの外径を表します。
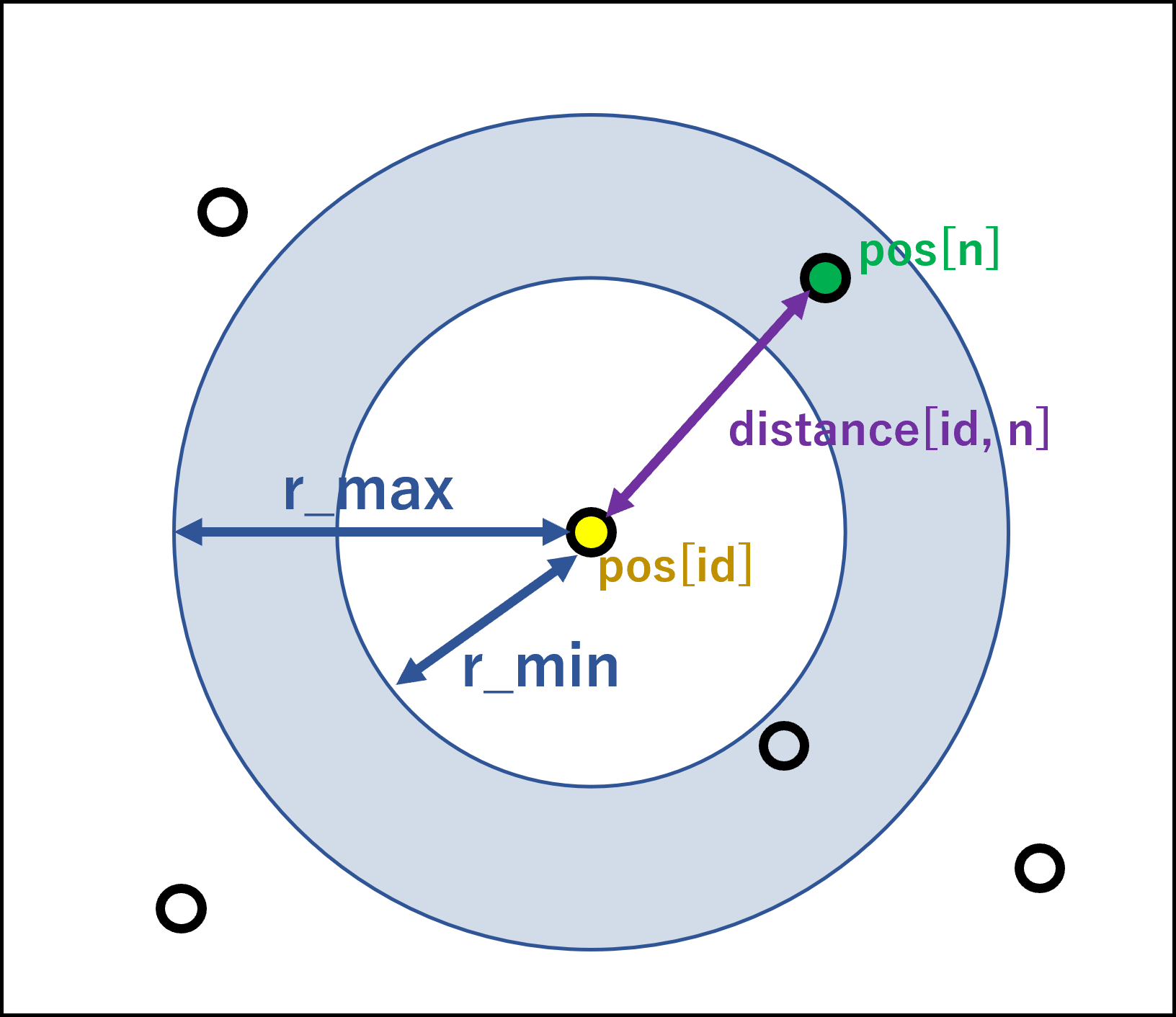
まずはドーナツ領域内にいる鳥の座標のインデックス(位置)を取得するところから。
# 2.[r_minとr_maxの間の範囲内にいる鳥さんたちの重心を教えてくれる関数] ※Center of Gravityで重心なのでCG
def GetCG(id, r_min, r_max) :
d = distance[id]
inRange = np.where((d > r_min) & (d < r_max)) [0]
以降では分かりやすさを重視して、以下のような具体的な値を仮設置した距離行列で考えていきます。
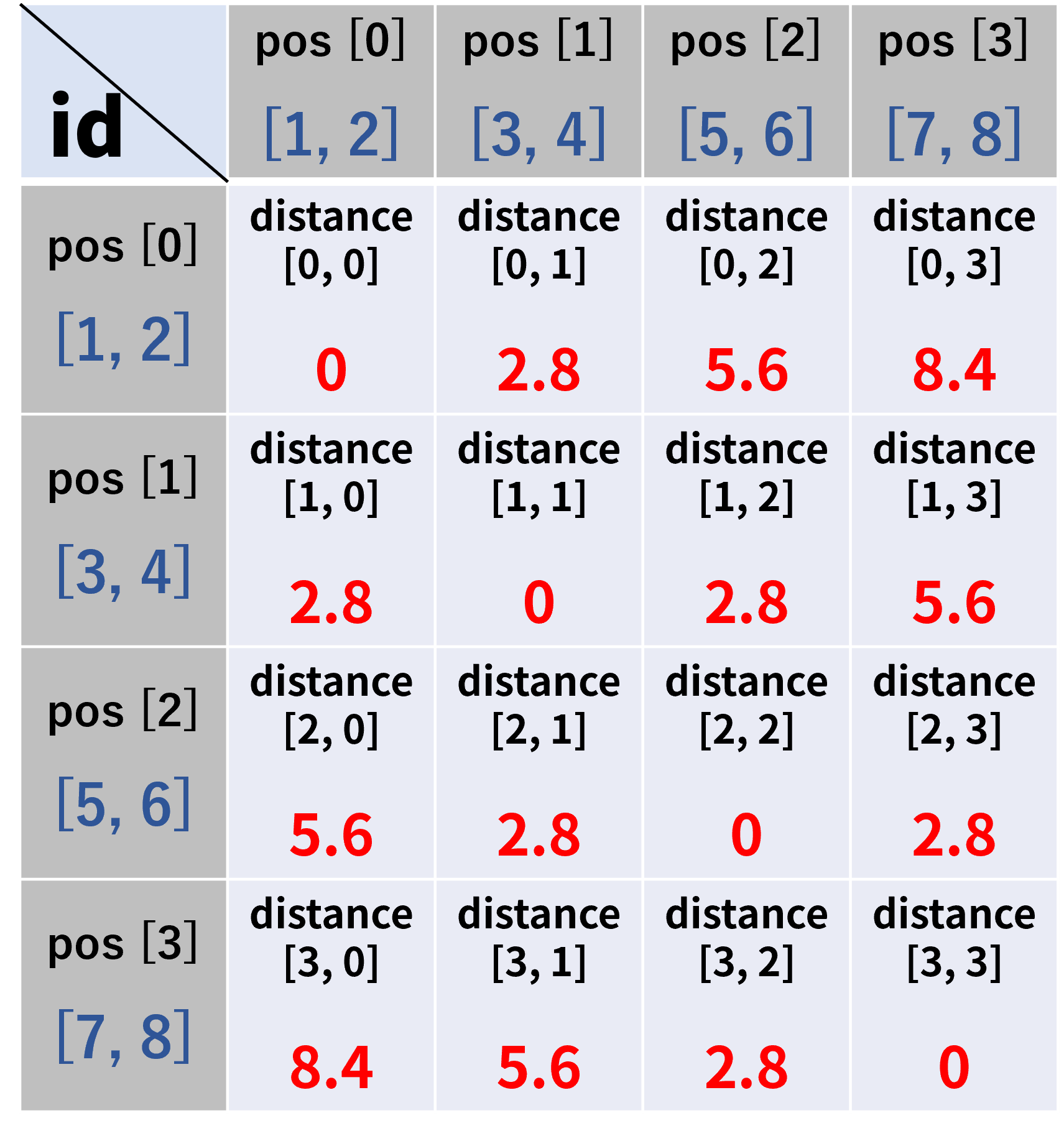
まず、距離行列の中からdistance[id]を抜き出し、dに格納します。
例えばid = 2で考えると、dにはpos[2]と他の鳥との距離の配列である
[5.6, 2.8, 0, 2.8]という1次元配列が格納されることになります。

次にnp.where((d > r_min) & (d < r_max)) [0]
によって、dの中からドーナツ領域の範囲内、つまりr_minとr_maxの間にいる鳥のインデックス(位置)を探し、inRangeの中に格納します。
インデックス(位置)だと分かりにくいですが、つまりは最初から数えて何番目かのことです。
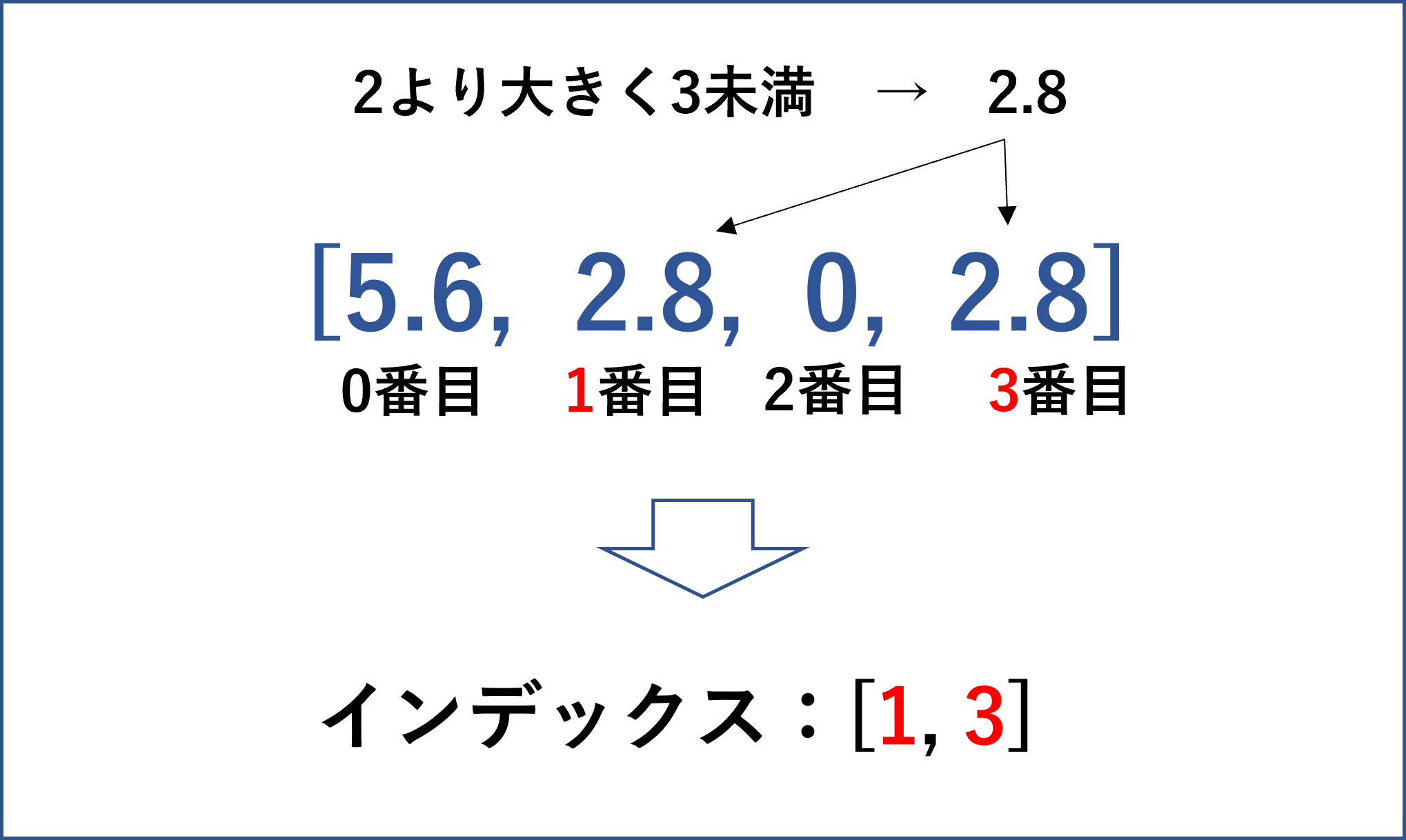
具体的に考えてみます。id = 2, r_min = 2, r_max = 3の場合、
[5.6, 2.8, 0, 2.8]の中から2より大きく3未満の値、すなわち2.8が選ばれます。そして2.8は最初から数えて1番目と3番目なので、最終的にinRnage には[1, 3]がインデックスとして格納されることになります。
(※今回のようにnp.where()の引数に条件文だけを指定すると、ndarrayのタプルとして結果が返ってくる。
仮に[0]を抜いてnp.where((d > r_min) & (d < r_max))にしてみると、
array([1, 3], dtype=int64)という結果が返ってくる。必要なのは最初の1次元配列[1, 3]だけなので[0]を付けてスライスしている。)
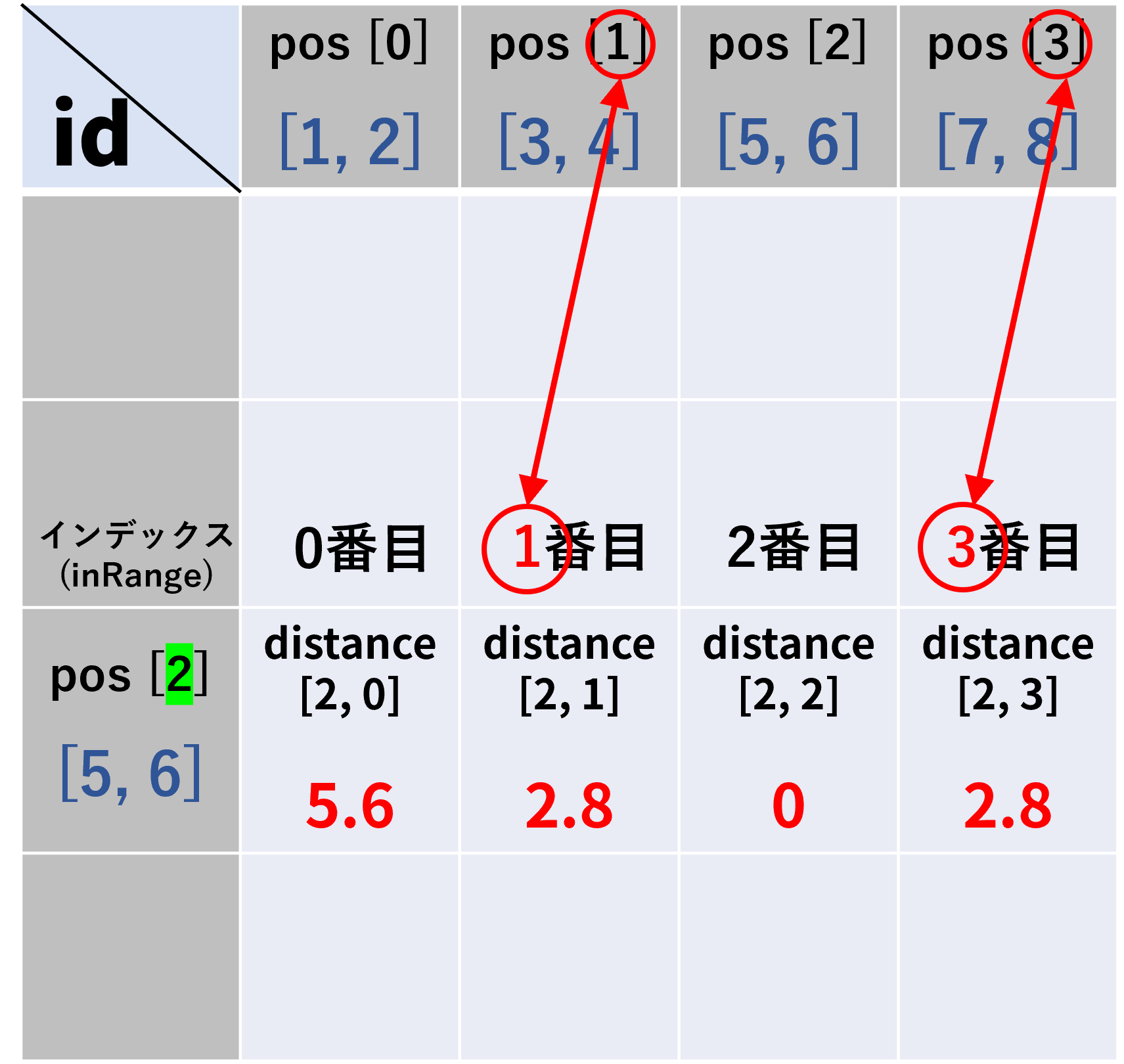
このようにして得られたインデックスinRangeは、鳥に割り振られた番号と一致しています。
つまり、inRrangeとは、ドーナツ領域内にいる鳥の背番号( = id )が並んだ配列です。
したがって、pos[inRange]によって、ドーナツ領域内にいる鳥の実際の座標を求めることができます。
例によってid = 2で考えると、inRangeは[1, 3]なので、pos[1]とpos[3]の座標である[3, 4]と[7, 8]を得ることができます。
ドーナツ領域にいる鳥の座標が分かったので、ようやく重心を求めることができるようになった。。。とその前に、例外処理をしておく必要があります。
例外とはすなわち、inRange == 0の場合、つまりドーナツ領域内に鳥がいない状況のことです。
そのような場合、鳥はその場から動かないことになってしまいます。別にじっとしていてもらっても構わないのですが、その場にうずくまってしまうのはあまり鳥の群れっぽくないので、少しモゾモゾしてもらうことにします。
つまり、自分の座標を少しだけランダムにずらします。
# ドーナツ内に仲間の鳥がいなかったら、自分の座標をランダムにずらしたものを返す
if len(inRange) == 0 :
cg = pos[id] + ((np.random.rand(2) * 2 - 1) * 0.0002) # 0.0002は適当に決めた
return cg
np.random.rand(2)では0以上1未満の(x、y)座標が生成されるので、そのまま足すだけでは右上方向に移動するようになってしまいます。4方向に均等に移動するためには、まず* 2で移動範囲を拡張し、次に- 1で移動範囲の中心をpos[id]に合わせる必要があります。
以下の図では、pos[id]を(0, 0)と設定して説明しています。
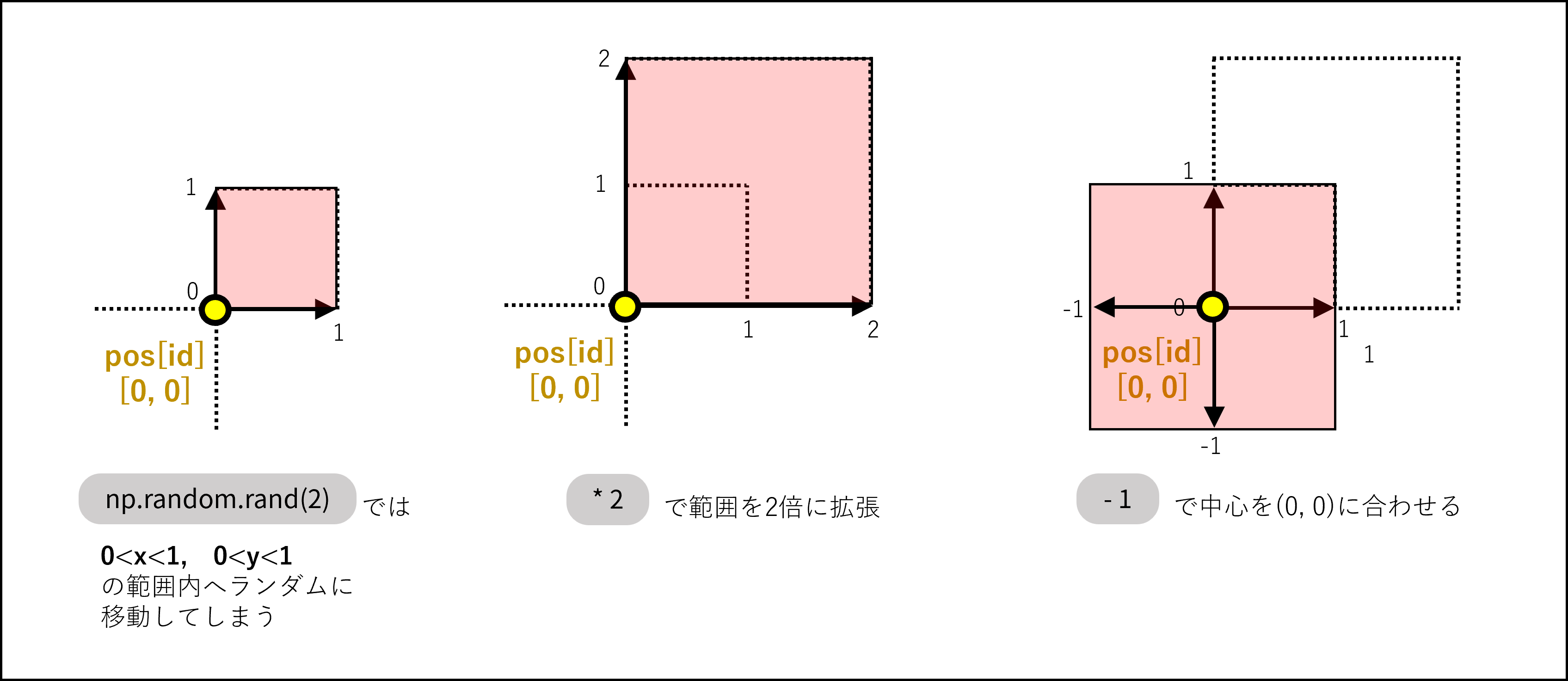
※図内の不等号を間違えて0<にしているが、「0以上」なので正しくは0≦。
(* 0.0002は適当に決めた。数字を変えれば、鳥のモゾモゾ具合を調節できる。)
例外処理が終わったので、ようやく重心の計算に入ります。
といっても、重心の計算自体はドーナツ領域内の鳥の座標の平均値を出せばいいだけなので、
配列要素の平均値を出す関数np.mean()にpos[inRange]を渡してあげればいいだけ。
#ドーナツ内にいる鳥の座標の平均を返す
else :
cg = np.mean(pos[inRange], axis = 0)
return cg
axis = 0を引数に指定しているのは、x座標どうし、y座標どうしの平均を出すため。
3. 仲間の進行方向の平均を求める

結合・分離ベクトルは重心だけで計算できるが、整列ベクトルを計算するためには仲間の進行方向も必要になります。そこで、ドーナツ範囲内にいる仲間の鳥の進行方向ベクトルを取得し、それらの平均を返す関数を
GetVEC(id, r_min, r_max)として作っておきます。
ドーナツ領域内にいる仲間の鳥の座標のインデックスをinRangeとして取得し、例外処理をするところまでは、重心とまったく同じ。
λ = np.pi / 3 # 視野の角度
def GetVEC(id, r_min, r_max) :
d = distance[id]
inRange = np.where((d > r_min) & (d < r_max)) [0]
if len(inRange) == 0 :
return 0
※前項のGetCG()では、ドーナツ領域内に誰もいなかった場合に自分の座標をランダムにずらしていたが、今回は特に何もしない。なのでreturn 0にしている。
ここから少し処理が異なってきます。
自分が群れの中の鳥になった想像してください。実際に仲間の鳥の動きに合わせようとするのなら、単に近くにいる仲間ではなく、目の前にいる仲間の動きに注目するはずです。
それを実現するためには、単なるドーナツ領域を設定するだけではなく、「視野」の要素が必要になります。
そこで、以下の図のように扇形の領域を追加し、ドーナツ領域内でかつ、扇型領域内の鳥の進行方向ベクトルを取得することにします。
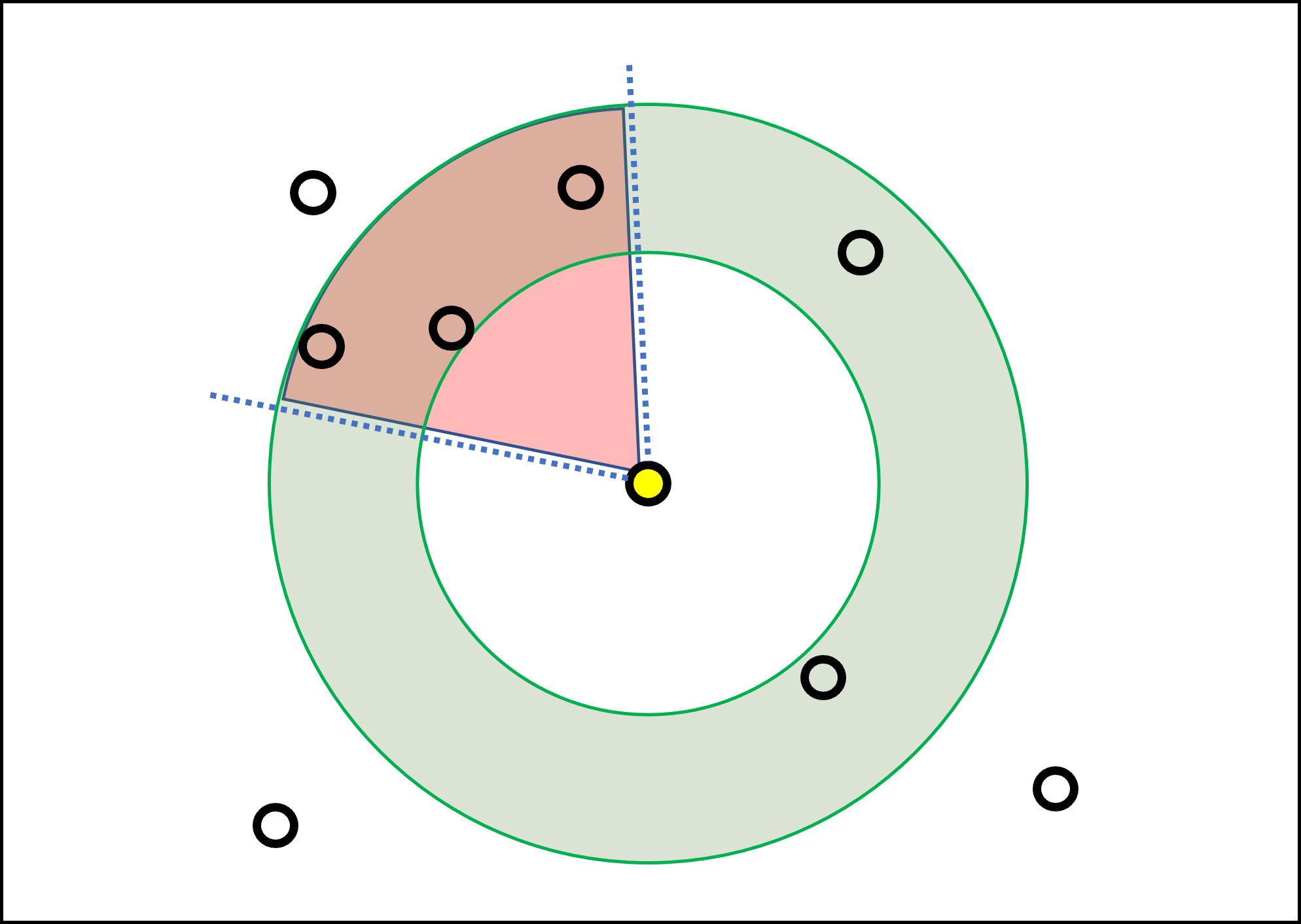
扇形領域は、下図のように設定。
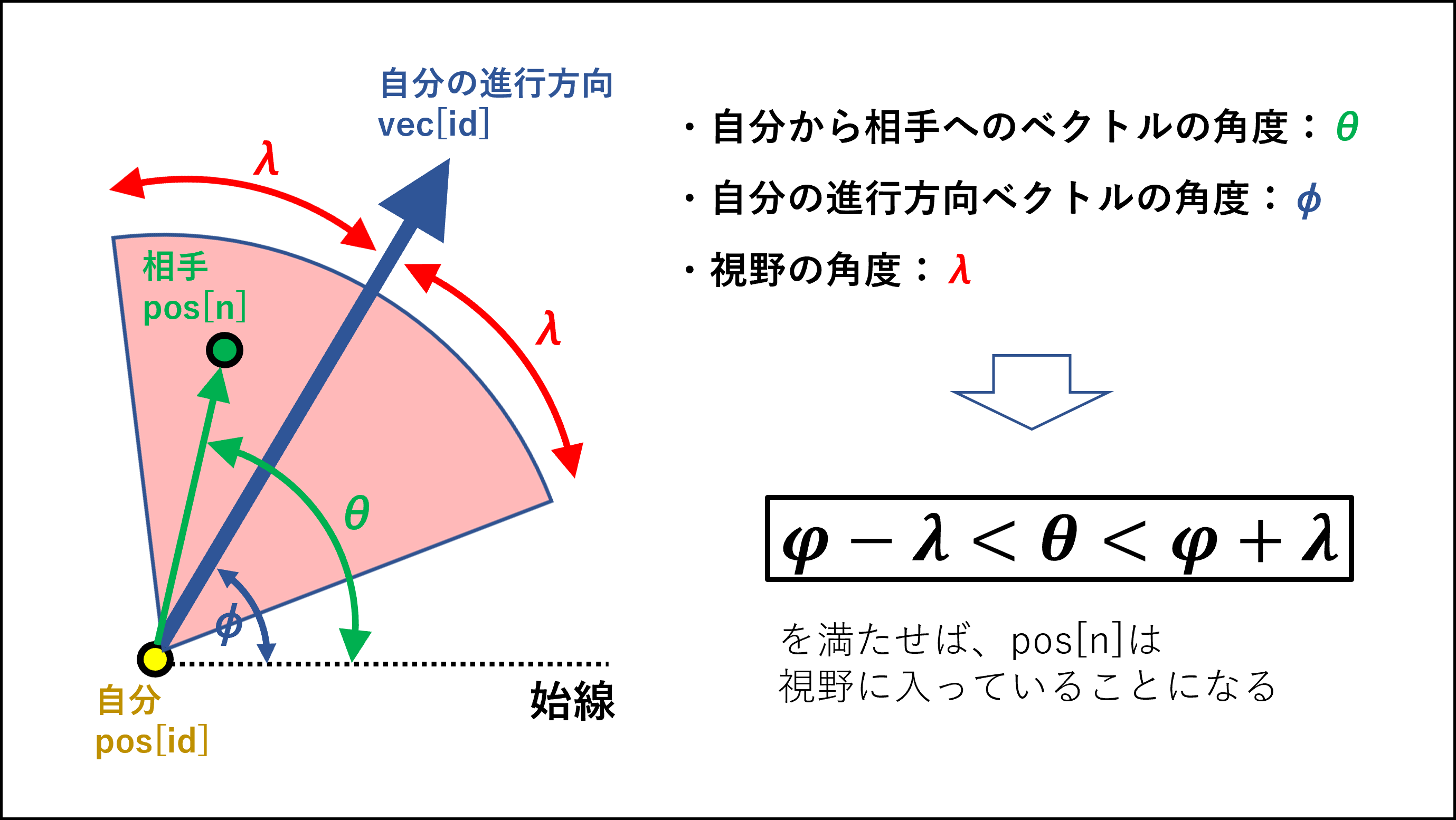
要するに θ・φ・λ の3つを先に計算しておき、$${φ-λ<θ<φ+λ}$$の条件を満たす鳥をあぶり出してやればOK。
else :
passlist = [] # 空のリスト。ここに視野にいる鳥の進行方向ベクトルを追加していく
for i in range(len(inRange)) :
line_vec = pos[inRange][i] - pos[id] # 自分と相手を結んだ直線のベクトル
θ = np.arctan2(line_vec[1], line_vec[0]) # 自分と相手を結んだ直線のベクトルの角度
φ = np.arctan2(vec[id][1], vec[id][0]) # 自分の現在の進行方向ベクトルの角度
if ((φ-λ) < θ) & (θ < (φ+λ)) :
passlist.append([vec[inRange][i]]) # 視野にいた鳥の進行方向ベクトルをpasslistに追加
else :
pass
inRangeはドーナツ領域内にいる鳥たちの背番号の配列なので
for文の中でpos[inRange][i]とし、1匹ずつ取り出して計算しています。
そしてforで背番号を回していく中で、条件に合格した鳥のベクトルだけ抜き出します。
抜き出してきたベクトルはとりあえずpasslistの中に.append()で放り込んでいく(ベクトルの平均はあとで計算する)、、、というのが大まかな流れです。
θ と φ の計算にはnp.arctan2()を使用しています。この関数は、引数に(y成分、x成分)を放り込むと、そのベクトルの偏角を返してくれる便利なヤツ。引数の順番が y成分、x成分 になっていることに注意する必要があります。
forを抜けると、ドーナツ領域内でかつ扇形領域内にいる鳥の進行方向ベクトルの全てがpasslistの中に保存された状態になります。
したがって、それらの平均を求めるためには、前項同様np.mean()にpasslistを放り込めばOK。
if len(passlist) == 0 : # 例外処理
return 0
else :
pg = np.mean(passlist, axis = 0) # ベクトル平均の計算
return pg
ドーナツ領域内にはいたが扇形領域の外だった鳥のために、if len(passlist) == 0で例外処理を行っています。
4. 壁に近づいたら反発させる
Boidsアルゴリズム自体は、これまで作ってきた関数だけで完成させることができます。しかし、このままでは鳥がグラフの外に飛び立ってしまい、描画できなくなってしまうことがあります。そこで描画領域内に鳥を閉じ込めるために、鳥が壁に近づいたら反射せる関数をGetRepulsion(id)として用意しておきます。
def GetRepulsion(id) :
# 壁との垂直距離
left = pos[id][0] - 0 # 左壁との距離
right = width - pos[id][0] # 右壁との距離
under = pos[id][1] - 0 # 下壁との距離
upper = width - pos[id][1] # 上壁との距離
# 壁との距離が1未満だったら、反対方向に反射させる。ベクトルのデカさは距離の2乗に反比例させて、壁に近ければ近いほど反発力を高める
if (left < 1) :
vec_LEFT = np.array([1,0]) / (left**2)
else :
vec_LEFT = 0
if (right < 1) :
vec_RIGHT = np.array([-1,0]) / (right**2)
else :
vec_RIGHT = 0
if (under < 1) :
vec_UNDER = np.array([0,1]) / (under**2)
else :
vec_UNDER = 0
if (upper < 1) :
vec_UPPER = np.array([0,-1]) / (upper**2)
else :
vec_UPPER = 0
# 4方面それぞれの反発ベクトルを合成
vec_R = vec_LEFT + vec_RIGHT + vec_UNDER + vec_UPPER
return vec_R
条件分岐を冗長に書いているせいで長ったらしいですが、原理は極めて単純。壁との垂直距離が1未満になったら、その壁と反対方向に働くベクトルを距離の2乗に反比例するように生成しているだけです。
距離の2乗に反比例させているのは、いわゆる逆2乗の法則というヤツ。物理ナニモワカラナイマンなので詳しくないが、自然界の物理現象に多くみられるらしい。これをやっとけば、とりあえず自然物っぽく見えるようになる。(過去の偉人が自然の中から導き出した"真理"を使って自然物をシミュレーションできるというのは、プログラミングで得られるカタルシスの1つなんじゃない?と初心者ながら思ってみたり...)
5. mainで動かす
関数を全部作り終わったので、mainで鳥を動かしていきます。
おまじない
ArtistAnimation でパラパラ漫画的な感じでアニメーションを動かすのだが、最初でその準備をしておく必要がある。ArtistAnimation については後で詳しく説明するので、現時点ではおまじないだと思ってもらって構いません。
import matplotlib.pyplot as plt
from matplotlib.animation import ArtistAnimation
fig = plt.figure() # 描画領域の確保
img_list = [] # パラパラ漫画の1枚1枚を保存する空の容器(list)
1行目のfigはガチのおまじないなので気にしなくて大丈夫。
2行目のimg_listは少し知っておく必要があります。ArtistAnimationはパラパラ漫画だとしつこく言っていますが、パラパラ漫画にするための1枚ずつのグラフをため込んでおく保存容器が必要になります。それがこのimg_lilst。後でこの箱の中身をパラパラめくることになります。
一時的な保存容器
以降では鳥の背番号idをforで回しながら距離行列distanceの中身を計算していくことになりますが、ここで逐一pos[id]やvec[id]を更新してしまうと、idの背番号によって更新される順番ができてしまい、実際の座標と距離行列の間に齟齬が生じてしまいます。
これを防ぐためには、forを抜けてすべてのpos[id] vec[id]を計算し終えた後に、距離座標distanceを一気に更新する必要があります。そこで、以下のような仮の保存容器の中に一時保存しておき、後から一気にpos vecを更新することにします。
p_pos = np.zeros([num_of_birds, 2]) # 一時的に新しい座標を保存しておくための空の容器(ndarray)
p_vec = np.zeros([num_of_birds, 2]) # 一時的に新しいベクトルを保存しておくための空の容器(ndarray)
Boidsの本質的なソースコード
ここからようやくBoidsアルゴリズムの本質的な内容になります。本記事の一番最初に記した「Boidsって何?」の項を思い出しながら見てほしいです。
r_min_c = 0.4 # 近づきたい鳥の範囲の内側
r_max_c = 2.2 # 近づきたい鳥の範囲の外側
r_min_s = 0 # 離れたい鳥の範囲の内側
r_max_s = 0.4 # 離れたい鳥の範囲の外側
r_min_a = 0.4 # 整列したい鳥の範囲の内側
r_max_a = 2.2 # 整列したい鳥の範囲の外側
k1 = 1 # 結合係数
k2 = 25 # 分離係数
k3 = 12 # 整列係数
e = 200 # 反発係数
v = 0.12 # 鳥の移動スピード
step = 500 # 試行回数(パラパラ漫画の枚数)
for n in range(step) : # パラパラ漫画の枚数(step)分回す
DISTANCE() # 距離行列を作成。stepを経るごとに距離座標は更新される
for id in range(num_of_birds) : # 鳥の数(num_of_birds)分回す
# お近づきになりたい鳥さんたちの座標の平均
Cohesion = GetCG(id = id, r_min = r_min_c, r_max = r_max_c) - pos[id]
# 距離をおきたい鳥さんたちの座標の平均
Separation = GetCG(id = id, r_min = r_min_s, r_max = r_max_s) - pos[id]
# 一緒に行動したい鳥さんたちのベクトルの平均
Alignment = GetVEC(id = id, r_min = r_min_a, r_max = r_max_a)
# 壁に対しての反発ベクトル
Repulsion = GetRepulsion(id = id)
# 進むべきベクトルを計算して、絶対値で割って単位ベクトル化
vec_T = vec[id] + k1* Cohesion - k2* Separation + k3* Alignment + e* Repulsion
vec_T /= np.linalg.norm(vec_T)
p_pos[id] = pos[id] + vec_T * v # p_posに新しい座標を保存
p_vec[id] = vec_T # p_vecに新しいベクトルを保存
pos = p_pos # 座標を一気に更新
vec = p_vec # ベクトルを一気に更新
# x座標、y座標として登録し、散布図にプロット
x = pos[:, 0]
y = pos[:, 1]
img = plt.scatter(x, y, s = 3, c= 'blue', marker= '1')
img_list.append([img]) # 出来上がった散布図1枚を、img_list の中に保存
一番外側のfor i in range (step)の中で、1枚の散布図を作成することになります。
散布図を作成するにあたり、まず最初に鳥の座標posをもとにDISTANCE()で距離行列を作成します。
距離行列ができたらfor id in range(num_of_birds) でidを回しながら、鳥1匹についての進行方向ベクトルを計算します。その計算過程で今まで作ってきた関数を使用します。すなわち、以下の4つです。
-
結合ベクトル :
Cohesion = GetCG() - pos[id] -
分離ベクトル :
Separation = GetCG() - pos[id] -
整列ベクトル :
Alignment = GetVEC() -
反発ベクトル :
Repulsion = GetRepulsion()
GetCG()が返すのはベクトルではなくただの重心の座標なので、
CohesionとSeparationでは- pos[id]によってベクトル化していることに注意。
4つのベクトルが計算し終わったら、それぞれに重み(k1, k2, k3, e)をかけて足し合わせ、
最終的な進行方向であるvec_Tを算出する。vec_Tは絶対値で割ることで、正規化します。
そしてvec_Tに移動速度vをかけたものを現在の座標pos[id]に足すことで、次の座標を算出します。このとき、次の座標は一旦p_posに仮置きしておきます。
また、vec_Tはそのまま次の進行方向ベクトルになるので、vec_T単体でp_vecに保存しておきます。
以上のベクトル計算が全部の鳥で終わると、1つ目のforを抜けます。
ここでpos = p_pos vec = p_vecにより座標・進行方向ベクトルを一気に更新。これによって、パラパラ漫画の次の1ページを作る際に、距離行列distanceも一気に更新されることになります。
最後に、新しくなったposの座標をグラフ上にプロットして、散布図を作成します。
散布図の作成には、matplotlib のplt.scatter()を用いています。引数が意味しているのは、それぞれ以下の通り。
-
x, y: プロットしたい点のx座標、y座標 -
s: 点の大きさ -
c: 点の色 -
marker: 点の形
このようにして完成した散布図imgを、本項の最初に作っておいたimg_listの中に.append()によって追加。
以上の工程を、パラパラ漫画の枚数step分だけ繰り返します。
全部終わると、img_listの中にすべての散布図がため込まれた状態になっています。あとはここから中身を取り出してパラパラめくれば、アニメーションの完成。
ArtistAnimation で描画
matplotlibについては分かりやすいネット記事が死ぬほどたくさん転がっている(YouTubeに動画もある)ので、わざわざこの項を読む必要はないです。ただしこの記事は自分の備忘録も兼ねているので、今回使っている要素に関しては最低限説明しておこうと思います。
今回使用している ArtistAnimationは先にフレームを全部作り置きしておき、一気にパラパラ漫画みたくめくってアニメーションにする仕組みです(溜めて解放理論)。
ArtistAnimation で基本になるのは、以下に記すanimオブジェクト。
anim = ArtistAnimation( fig, artists, interval, blit )
引数に指定されているのは、それぞれ
-
fig: 描画領域 -
artists: グラフ画像をため込んだリスト -
interval: フレームをパラパラめくる間隔 -
blit: Trueにするとアニメーションが最適化されるらしい(よく分かんない)
1つ目のfigと4つ目のblitはほぼおまじないみたいなもので、3つ目のintervalも定数として指定すればいい。
ちゃんと理解しなければいけないのは、2つ目のartists。ここに前項で作ったimg_listを渡します。
ts = 25 # フレーム間隔
anim = ArtistAnimation(
fig = fig,
artists = img_list, # さっき作った散布図のリストを渡している
interval = ts,
blit = True
)
あとはグラフの描画範囲を指定して、Show ! すれば完成。
plt.xlim(0, width) # x軸方向の描画範囲
plt.ylim(0, width) # y軸方向の描画範囲
plt.show()
完成。
終わりに
パラメータだけかき集めると、こんな感じ
# ==========パラメータ====================
num_of_birds = 100 # 鳥の数
step = 500 # 試行回数
width = 25 # フィールド正方形の1辺
ts = 25 # 描画スピード
r_min_c = 0.4 # 近づきたい鳥の範囲の内側
r_max_c = 2.2 # 近づきたい鳥の範囲の外側
r_min_s = 0 # 離れたい鳥の範囲の内側
r_max_s = 0.4 # 離れたい鳥の範囲の外側
r_min_a = 0.4 # 整列したい鳥の範囲の内側
r_max_a = 2.2 # 整列したい鳥の範囲の外側
k1 = 1 # 結合係数
k2 = 25 # 分離係数
k3 = 12 # 整列係数
v = 0.12 # 鳥の移動スピード
e = 200 # 反発係数
λ = np.pi / 3 # 鳥の視界の範囲
# ===========================================
数値設定は実際にシミュレーションを繰り返している中で「なんか群れっぽくなった!」と思ったものを適当に採用しています。いろいろ変えて遊んでみるとおもしろいよ。

