量子機械学習ワークショップQTML2017の発表スライド『Quantum Neuron』と、その論文『Quantum Neuron: an elementary building block for machine learning on quantum computers』を読みはじめました。初めの章からしてパズル的に面白くて、ちょっと魔法みたいだったので紹介してみます。
なお、この論文は量子ゲート計算機でニューラルネットワークを実装しようという話で、ややこしいですが、ImPACTの量子ニューラルネットワーク計算機とは別物です。
概要
まず、論文概要の前半をざくっと訳してみます。
どれだけ複雑なニューラルネットワークであろうと、人工ニューロンの集合体であることに変わりはありません。そして人工ニューロンとは、複数の信号を受けとり線形結合したあと、非線形関数を適用するものです。
量子の枠組みで人工ニューロンを作る方法がいくつか提案されてきましたが、量子は線形な振る舞いをするため、人工ニューロンの要である非線形な活性化関数を実装することが困難でした。
本論文では、その問題を解決するため、ステップ関数を模擬する小さな量子回路を提案します。
そうなんですよね。量子ビットの状態計算は複素数行列の掛け算で表されるので、普通に考えると線形関数しか実装できなさそうに思えます。
で、実際に人工ニューロンをどう実装しているか、論文のFigure 1を引用すると、

(a) 古典的な計算グラフ
(b) ブロッホ球による計算グラフ
(c) 量子回路
(d) 活性化関数のグラフ
というわけです! なるほどー???
具体的には、ブロッホ球のY軸回転、成功するまで測定を繰り返す回路、の組み合わせがテクニカルで面白いのですが、論文では詳しい計算が省略されていて面食らったので、そのあたり補完しながら紹介していきます。怪しいところあったら教えてネ。
それで、量子的な人工ニューロンができると何が嬉しいかというと、
我々は「量子ニューロン」を実装し、古典的なニューラルネットワークの幾つかを構築できることを示します。これは量子の重ね合わせ状態を、コヒーレンスとエンタングルメントの性質を保ったまま処理できるものです。
ということで単純に考えれば、ニューラルネットワークの入力層が $n$ 量子ビットあれば、 $2^n$ 個のデータを重ね合わせて一気に学習できるっていうことですね。おほー。こいつぁすげぇや。
人工ニューロンの数式
入力 $x_i \in { 0, 1}$ 重み $w_i$ バイアス $b$ の線形結合 $\theta$ を次のように計算して、
$\theta = w_1 x_1 + \cdots + w_n x_n + b$
これを活性化関数 $\sigma$ に食わせた $\sigma(\theta)$ を出力するのが、基本的な人工ニューロンの数式です。
論文では $\sigma$ として、次の非線形関数を利用します。ちょいとばっかしゴツいですね?
\begin{align}
q(\phi) &= \arctan(\tan^2 \phi) \\
q^{\circ k}(\phi) &= q( \cdots q(\phi)) = \arctan(\tan^{2^k} \phi) \\
\lim_{k \to \infty} q^{\circ k}(\phi) &= \begin{cases}
0 & (0 < \phi < \frac{\pi}{4}) \\
\frac{\pi}{2} & (\frac{\pi}{4} < \phi < \frac{\pi}{2})
\end{cases}
\end{align}
ブロッホ球の回転計算
もう一つ準備として、ブロッホ球の回転計算を見ておきます。
まず、パウリゲート $X, Y, Z$ の行列は次のとおりで、
X = \begin{pmatrix}
0 & 1 \\
1 & 0 \\
\end{pmatrix}, \
Y = \begin{pmatrix}
0 & -i \\
i & 0 \\
\end{pmatrix}, \
Z = \begin{pmatrix}
1 & 0 \\
0 & -1 \\
\end{pmatrix}
それぞれブロッホ球で考えると、x軸180度回転、y軸180度回転、z軸180度回転、にあたります。
これを元に『Rotations on the Bloch Sphere』のとおり、x軸 $\phi$ ラジアン回転 $R_x(\phi)$ 、y軸 $\phi$ ラジアン回転 $R_y(\phi)$ 、z軸 $\phi$ ラジアン回転 $R_z(\phi)$ 、を計算できます。$\sim$ はグローバル位相による同値関係とします。
\begin{align}
R_x(\phi) &= e^{-i X \frac{\phi}{2}} = \cos \frac{\phi}{2} I - i \sin \frac{\phi}{2} X = \begin{pmatrix}
\cos \frac{\phi}{2} & -i \sin \frac{\phi}{2} \\
-i \sin \frac{\phi}{2} & \cos \frac{\phi}{2} \\
\end{pmatrix} \\
R_y(\phi) &= e^{-i Y \frac{\phi}{2}} = \cos \frac{\phi}{2} I - i \sin \frac{\phi}{2} Y = \begin{pmatrix}
\cos \frac{\phi}{2} & - \sin \frac{\phi}{2} \\
\sin \frac{\phi}{2} & \cos \frac{\phi}{2} \\
\end{pmatrix} \\
R_z(\phi) &= e^{-i Z \frac{\phi}{2}} = \cos \frac{\phi}{2} I - i \sin \frac{\phi}{2} Z = \begin{pmatrix}
e^{- i \frac{\phi}{2}} & 0 \\
0 & e^{i \frac{\phi}{2}} \\
\end{pmatrix} \sim \begin{pmatrix}
1 & 0 \\
0 & e^{i \phi} \\
\end{pmatrix} \\
\end{align}
ここで $e$ の肩にパウリゲート乗っていてギョッとするかもしれませんが、
e^{i \theta}
= \sum^{\infty}_{n=0} \frac{(i \theta)^n}{n!}
= \sum^{\infty}_{n=0} \frac{(-1)^n}{(2n)!}x^{2n} \ + \ i \sum^{\infty}_{n=0} \frac{(-1)^n}{(2n + 1)!}x^{2n + 1}
= \cos \theta + i \sin \theta
という普通のテイラー展開の拡張として、正方行列の指数関数を定義することができます。
そのため $A^2 = I$ なる正方行列 $A$ があったとき、次を満たすというわけですね。
e^{i A \phi}
= \sum^{\infty}_{n=0} \frac{(i A \phi)^n}{n!}
= \left( \sum^{\infty}_{n=0} \frac{(-1)^n}{(2n)!}\phi^{2n} \right) I \ + \ i \left( \sum^{\infty}_{n=0} \frac{(-1)^n}{(2n + 1)!}\phi^{2n + 1} \right) A
= \cos \phi I + i \sin \phi A
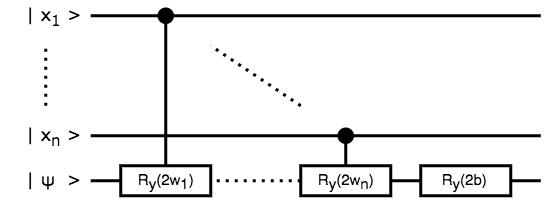
線形結合の量子回路
では、量子回路を組んでいきます。
この量子ビットの状態を左から右へ追うと、
\newcommand{\ket}[1]{\left| #1 \right\rangle}
\begin{align}
\ &\ket{x_1 \dots x_n} \otimes \ket{\psi} \\
\xrightarrow[\mathrm{controlled} \ R_y(2 w_1)]{}
\ &\ket{x_1 \dots x_n} \otimes R_y(2 w_1 x_1) \ket{\psi} \\
&\vdots \\
\xrightarrow[\mathrm{controlled} \ R_y(2 w_n)]{}
\ &\ket{x_1 \dots x_n} \otimes R_y(2 w_n x_n) \dots R_y(2 w_1 x_1) \ket{\psi} \\
\xrightarrow[R_y(2 b)]{}
\ &\ket{x_1 \dots x_n} \otimes R_y(2 b) R_y(2 w_n x_n) \dots R_y(2 w_1 x_1) \ket{\psi} \\
= \ &\ket{x_1 \dots x_n} \otimes R_y(2 b + 2 w_n x_n + \dots + 2 w_1 x_1) \ket{\psi} \\
= \ &\ket{x_1 \dots x_n} \otimes R_y(2 \theta) \ket{\psi} \\
\end{align}
はい、ブロッホ球のY軸回転で線形結合 $\theta$ を表現することができました。
入力の量子状態 $\ket{x_1 \dots x_n}$ は使いまわすので、そちらには干渉していないのもポイントです。
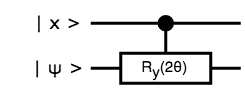
以後 $\ket{x} = \ket{x_1 \dots x_n}$ として、下図で省略することにします。
活性化関数の量子回路
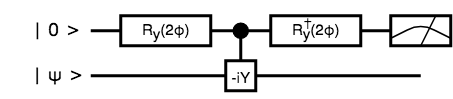
さて、ここからが本番です。
これは下図と同じで、
この量子ビットの状態を左から右へ追うと、
\begin{align}
\ &\ket{0} \otimes \ket{\psi} \\
\xrightarrow[R_y(2 \phi)]{}
\ &( \ \cos \phi I \ket{0} - i \sin \phi Y \ket{0} \ ) \otimes \ket{\psi} \\
= \ &\cos \phi \ket{0} \otimes \ket{\psi} + \sin \phi \ket{1} \otimes \ket{\psi} \\
\xrightarrow[\mathrm{controlled} \ -i Y]{}
\ &\cos \phi \ket{0} \otimes \ket{\psi} - i \sin \phi \ket{1} \otimes Y \ket{\psi} \\
\xrightarrow[R_y(2 \phi)^\dagger]{}
\ &\cos \phi ( \ \cos \phi I \ket{0} + i \sin \phi Y \ket{0} \ ) \otimes \ket{\psi} - i \sin \phi ( \ \cos \phi I \ket{1} + i \sin \phi Y \ket{1} \ ) \otimes Y \ket{\psi} \\
= \ &\cos^2 \phi \ket{0} \otimes \ket{\psi} - \cos \phi \sin \phi \ket{1} \otimes \ket{\psi} - i \sin \phi \cos \phi \ket{1} \otimes Y \ket{\psi} - i \sin^2 \phi \ket{0} \otimes Y \ket{\psi} \\
= \ &\ket{0} \otimes ( \ \cos^2 \phi \ket{\psi} - i \sin^2 \phi Y \ket{\psi} \ ) - \sin \phi \cos \phi \ket{1} \otimes ( \ \ket{\psi} + i Y \ket{\psi} \ ) \\
= \ &\sqrt{cos^4 \phi + \sin^4 \phi} \ket{0} \otimes \left( \ \frac{1}{\sqrt{1 + \tan^4 \phi}} \ket{\psi} - i \frac{\tan^2 \phi}{\sqrt{1 + \tan^4 \phi}} Y \ket{\psi} \ \right) - \sqrt{2} \sin \phi \cos \phi \ket{1} \otimes R_y \left(- \frac{\pi}{2} \right) \ket{\psi} \\
= \ &\sqrt{\frac{\cos^2 2 \phi + 1}{2}} \ket{0} \otimes R_y(2 \arctan(\tan^2 \phi)) \ket{\psi} - \sqrt{\frac{\sin^2 2 \phi}{2}} \ket{1} \otimes R_y \left(- \frac{\pi}{2} \right) \ket{\psi} \\
= \ &\sqrt{\frac{\cos^2 2 \phi + 1}{2}} \ket{0} \otimes R_y(2 q(\phi)) \ket{\psi} - \sqrt{\frac{\sin^2 2 \phi}{2}} \ket{1} \otimes R_y \left(- \frac{\pi}{2} \right) \ket{\psi} \\
\end{align}
非線形関数 $q(\phi)$ キタ━━゚+.ヽ(≧▽≦)ノ.+゚━━ ッ !!!
あとは補助ビットを測定して、 $0$ であれば出力ビットが $R_y(2 q(\phi)) \ket{\psi}$ になっているっていう寸法です。
え、測定結果が $1$ だったらどうするかって? その時は出力ビット $R_y \left(- \frac{\pi}{2} \right) \ket{\psi}$ に $R_y \left(\frac{\pi}{2} \right)$ を適用して元に戻し、また同じことを繰り返せばいいのです。このような回路を、RUS (Repeat Until Success)と呼びます。
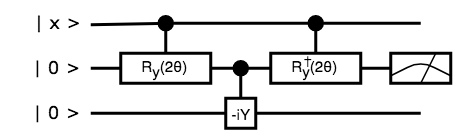
人工ニューロンの量子回路
あとは上図を組み合わせればよくて、
これは $R_y(2 q(\theta)) \ket{0}$ を出力して、さらにRUS回路を重ねれば、

$R_y(2 q(q(\theta))) \ket{0} = R_y(2 q^{\circ 2}(\theta)) \ket{0}$ を出力します。
同様に再帰した回路を組めば、 $R_y(2 q^{\circ k}(\theta)) \ket{0}$ を出力できるっていう寸法です。
\lim_{k \to \infty} R_y(2 q^{\circ k}(\theta)) \ket{0} = \begin{cases}
R_y(0) \ket{0} = \ket{0} & (0 < \theta < \frac{\pi}{4}) \\
R_y(\pi) \ket{0} = \ket{1} & (\frac{\pi}{4} < \theta < \frac{\pi}{2})
\end{cases}
$k$ を大きくすれば出力値が $\ket{0}, \ket{1}$ に漸近するので、これを新たな人工ニューロンの入力として、ニューラルネットワークの層を成すこともできそうですね。
論文では実際に、順伝播型ニューラルネットワークとホップフィールドネットワークを例にして、誤差を測って学習の収束具合を議論したりしているっぽいのですが、それはこれから読み進めていきたいと思います。
それでは量子コンピュータで、ディープラーニングをプログラミングできる未来を夢見て……!