Microsoftが2017年内に、量子コンピュータのための新しいプログラミング言語を公開するそうですね!
量子力学……波動関数……シュレディンガーの猫……。ええ、よく 中二病 SFで耳にする、なんかヤバいやつです。量子コンピュータが実用化されると、現在のインターネットで使われてる暗号はすぐに解けてしまうとか。 ちょっとネットで調べただけで知ったかぶらないでよ!
量子プログラミング言語自体はすでに幾つもありますが、今回のものはVisual Studioで開発・デバッグできてAzureのシミュレータでも動くとのことで、Microsoftの本気を感じます。言語的には、C#、Python、F#の要素を取り入れているらしく、モダンなものになるでしょう。まだ名前は決まってないそうですが。
ということで、夢の量子コンピュータがいよいよ実用的なソフトウェア領域にやってきそうな予感がしたので、付け焼刃の勢いでサンプルコードを読んでみました。 BGMは量子の海のリンドヴルムです。ニャ!
量子ビット計算
量子コンピュータには、NASAやGoogleが利用しているD-WAVEの量子アニーリング方式、IBMがクラウド公開しているIBM Qの量子ゲート方式、の二種類あります。そして、Microsoftの言語は量子ゲート用です。
量子ゲートは、量子ビットに作用します。普通のビットは0か1のどちらかしか表せませんが、量子ビットは0と1を重ね合わせた状態を取ることができます。たとえば、
\newcommand{\ket}[1]{\left| #1 \right\rangle}
\frac{1}{\sqrt{2}}\ket{00} + \frac{1}{\sqrt{2}}\ket{11}
は、量子ビットの一つ目が0で二つ目も0という状態と、量子ビットの一つ目が1で二つ目も1という状態が、同じ確率で重なり合った状態を表しています。このように複数の状態を重ね合わせたまま量子ゲートを作用させることで、普通のコンピュータを遥かに凌駕しうる超並列計算ができるというわけですね。 あとヨルムンガンドも発動します。
重ね合わせが物理的にどういう意味を持つのか、というところに踏みこむためには量子力学が必要ですが、量子ビットの計算自体はいくつかのルールを抑えてしまえば大丈夫です。
そのルールも簡単で、式変形を眺めているうちに自然と理解できると思うので、まずはサンプルコードに登場する量子ゲートを紹介します。
ビット反転ゲート X
\begin{align}
\mathrm{X}\ket{0} &= \ket{1} \\
\mathrm{X}\ket{1} &= \ket{0} \\
\end{align}
位相反転ゲート Z
\begin{align}
\mathrm{Z}\ket{0} &= \ket{0} \\
\mathrm{Z}\ket{1} &= -\ket{1} \\
\end{align}
アダマールゲート H
\begin{align}
\mathrm{H}\ket{0} &= \frac{1}{\sqrt{2}}\ket{0} + \frac{1}{\sqrt{2}}\ket{1} \\
\mathrm{H}\ket{1} &= \frac{1}{\sqrt{2}}\ket{0} - \frac{1}{\sqrt{2}}\ket{1}
\end{align}
制御ノットゲート CNOT
\begin{align}
\mathrm{CNOT}\ket{00} &= \ket{00} \\
\mathrm{CNOT}\ket{01} &= \ket{01} \\
\mathrm{CNOT}\ket{10} &= \ket{11} \\
\mathrm{CNOT}\ket{11} &= \ket{10}
\end{align}
サンプルコード
それでは、『Microsoft makes play for next wave of computing with quantum computing toolkit』で紹介されている、42行のサンプルコードを読んでいきましょう。量子アルゴリズム界隈におけるハローワールド、量子テレポーテーションをテストするコードです。量子テレポーテーション……かっこいい響き! Y軸を傾ければ時間も跳躍できますからね。
なお今のところ言語仕様は不明で、サンプルコードそのものしか手掛かりがないので、以下の説明は全て推測でしかないです。答え合わせが楽しみですね?
EPRペア関数
operation () EPR (Qubit q1, Qubit q2) {
Body {
H (q1)
CNOT (q1, q2)
}
}
EPRペアという、二つの量子ビットをもつれさせる関数です。
そうです、量子ビットはもつれたり重ね合わさったりする、可愛いやつなんです。
一行ずつ追っていきましょう。
operation () EPR (Qubit q1, Qubit q2) {
二つの量子ビット q1 q2 の状態を操作する関数 EPR を宣言しています。
q1 q2 ともに $\ket{0}$ である量子ビットが与えられたとして、 $\ket{\mathrm{q1}\ \mathrm{q2}}$ の状態変化を追ってみましょう。
\ket{00}
H (q1)
q1 にアダマールゲートを作用させます。
(\mathrm{H}\ket{0})\ket{0} = \frac{1}{\sqrt{2}}\ket{00} + \frac{1}{\sqrt{2}}\ket{10}
CNOT (q1, q2)
q1 q2 に制御ノットゲートを作用させます。
\frac{1}{\sqrt{2}}(\mathrm{CNOT} \ket{00}) + \frac{1}{\sqrt{2}}(\mathrm{CNOT} \ket{10}) = \frac{1}{\sqrt{2}}\ket{00} + \frac{1}{\sqrt{2}}\ket{11}
量子テレポーテーション関数
operation() Teleport (Qubit msg, Qubit here, Qubit there) {
Body {
EPR (here, there)
CNOT (msg, here)
H (msg)
let m_here = M (here)
if (m_here == One) {
X (there)
}
let m_msg = M (msg)
if (m_msg == One) {
Z (there)
}
}
}
おまちかね、量子テレポーテーションを行う関数です!
operation() Teleport (Qubit msg, Qubit here, Qubit there) {
三つの量子ビット msg here there の状態を操作する関数 EPR を宣言しています。
msg に $a\ket{0} + b\ket{1}$ here there には $\ket{0}$ である量子ビットが与えられたとして、 $\ket{\mathrm{msg}\ \mathrm{here}\ \mathrm{there}}$ の状態変化を追ってみましょう。
なお $a$ $b$ は $|a|^2 + |b|^2 = 1$ を満たす複素数です。
EPR (here, there)
\begin{align}
&a\ket{0}(\mathrm{EPR} \ket{00}) + b\ket{1}(\mathrm{EPR} \ket{00}) \\
=\quad &\frac{a}{\sqrt{2}}\ket{000} + \frac{a}{\sqrt{2}}\ket{011} + \frac{b}{\sqrt{2}}\ket{100} + \frac{b}{\sqrt{2}}\ket{111}
\end{align}
CNOT (msg, here)
\begin{align}
&\frac{a}{\sqrt{2}}(\mathrm{CNOT} \ket{00})\ket{0} + \frac{a}{\sqrt{2}}(\mathrm{CNOT} \ket{01})\ket{1} \\
&+ \frac{b}{\sqrt{2}}(\mathrm{CNOT} \ket{10})\ket{0} + \frac{b}{\sqrt{2}}(\mathrm{CNOT} \ket{11})\ket{1} \\
=\quad &\frac{a}{\sqrt{2}}\ket{000} + \frac{a}{\sqrt{2}}\ket{011} + \frac{b}{\sqrt{2}}\ket{110} + \frac{b}{\sqrt{2}}\ket{101}
\end{align}
H (msg)
\begin{align}
&\frac{a}{\sqrt{2}}(\mathrm{H}\ket{0})\ket{00} + \frac{a}{\sqrt{2}}(\mathrm{H}\ket{0})\ket{11} \\
&+ \frac{b}{\sqrt{2}}(\mathrm{H}\ket{1})\ket{10} + \frac{b}{\sqrt{2}}(\mathrm{H}\ket{1})\ket{01} \\
=\quad &\frac{a}{2}\ket{000} + \frac{a}{2}\ket{100} + \frac{a}{2}\ket{011} + \frac{a}{2}\ket{111} \\
&+ \frac{b}{2}\ket{010} - \frac{b}{2}\ket{110} + \frac{b}{2}\ket{001} - \frac{b}{2}\ket{101}
\end{align}
let m_here = M (here)
if (m_here == One) {
X (there)
}
if文による条件分岐が出てきました!
と、その前に M ですが、これは観測を行います。観測すると、もつれも重ね合わせも壊れてしまい、 here は $\ket{0}$ か $\ket{1}$ のどちらかに収束してしまいます。かわいーくなーい。
どちらになるかは神が振るサイコロ任せなので、それぞれ追ってみましょう。
-
m_here == Zeroの場合
\begin{align}
&\sqrt{2}(\frac{a}{2}\ket{000} + \frac{a}{2}\ket{100} + \frac{b}{2}\ket{001} - \frac{b}{2}\ket{101}) \\
=\quad & \frac{a}{\sqrt{2}}\ket{000} + \frac{a}{\sqrt{2}}\ket{100} + \frac{b}{\sqrt{2}}\ket{001} - \frac{b}{\sqrt{2}}\ket{101}
\end{align}
-
m_here == Oneの場合
\begin{align}
&\sqrt{2}(\frac{a}{2}\ket{01}(\mathrm{X} \ket{1}) + \frac{a}{2}\ket{11}(\mathrm{X} \ket{1}) + \frac{b}{2}\ket{01}(\mathrm{X} \ket{0}) - \frac{b}{2}\ket{11}(\mathrm{X} \ket{0})) \\
=\quad &\frac{a}{\sqrt{2}}\ket{010} + \frac{a}{\sqrt{2}}\ket{110} + \frac{b}{\sqrt{2}}\ket{011} - \frac{b}{\sqrt{2}}\ket{111}
\end{align}
let m_msg = M (msg)
if (m_msg == One) {
Z (there)
}
-
m_msg == Zero&m_here == Zeroの場合
\begin{align}
&\sqrt{2}(\frac{a}{\sqrt{2}}\ket{000} + \frac{b}{\sqrt{2}}\ket{001}) \\
=\quad &a\ket{000} + b\ket{001} \\
=\quad &\ket{00}(a\ket{0} + b\ket{1})
\end{align}
-
m_msg == One&m_here == Zeroの場合
\begin{align}
&\sqrt{2}(\frac{a}{\sqrt{2}}\ket{10}(\mathrm{Z} \ket{0}) - \frac{b}{\sqrt{2}}\ket{10}(\mathrm{Z} \ket{1})) \\
=\quad &a\ket{100} + b\ket{101} \\
=\quad &\ket{10}(a\ket{0} + b\ket{1})
\end{align}
-
m_msg == Zero&m_here == Oneの場合
\begin{align}
&\sqrt{2}(\frac{a}{\sqrt{2}}\ket{010} + \frac{b}{\sqrt{2}}\ket{011}) \\
=\quad &a\ket{010} + b\ket{011} \\
=\quad &\ket{01}(a\ket{0} + b\ket{1})
\end{align}
-
m_msg == One&m_here == Oneの場合
\begin{align}
&\sqrt{2}(\frac{a}{\sqrt{2}}\ket{11}(\mathrm{Z} \ket{0}) - \frac{b}{\sqrt{2}}\ket{11}(\mathrm{Z} \ket{1})) \\
=\quad &a\ket{110} + b\ket{111} \\
=\quad &\ket{11}(a\ket{0} + b\ket{1})
\end{align}
やりました!
msg here の観測結果に関わらず there の状態は $a\ket{0} + b\ket{1}$ になりました。
msg の量子的な状態が there にテレポートしたので、量子テレポーテーションというわけです。
テスト関数
operation (Result) TeleportTest (Result msg) {
Body {
mutable res = Zero
using (qubits = Qubit[3]) {
let msgQ = qubits[0]
// Set msgQ to message state
SetQubit (msg, msgQ)
Teleport (msgQ, qubits[1], qubits[2])
set res = M(qubits[2])
}
return res
}
}
見てのとおりテスト関数ですねっ。
operation (Result) TeleportTest (Result msg) {
Result 型の msg を受け取って、Result 型の値を返す関数 TeleportTest を宣言しています。
Result 型の値は Zero と One があります。
using (qubits = Qubit[3]) {
長さ3の量子ビット列を確保しています。
using のスコープ抜けるとリソース解放されます。
let msgQ = qubits[0]
量子ビット列 qubits の1番目の要素を変数束縛しています。
SetQubit (msg, msgQ)
Teleport (msgQ, qubits[1], qubits[2])
set res = M(qubits[2])
Result 型の msg の状態を Qubit 型の msgQ にセットして、 qubits の3番目の要素に量子テレポーテーションして、その観測結果を Result 型の res に代入します。
return res
最後に res を返します。めでたし、めでたし。
IBM Q
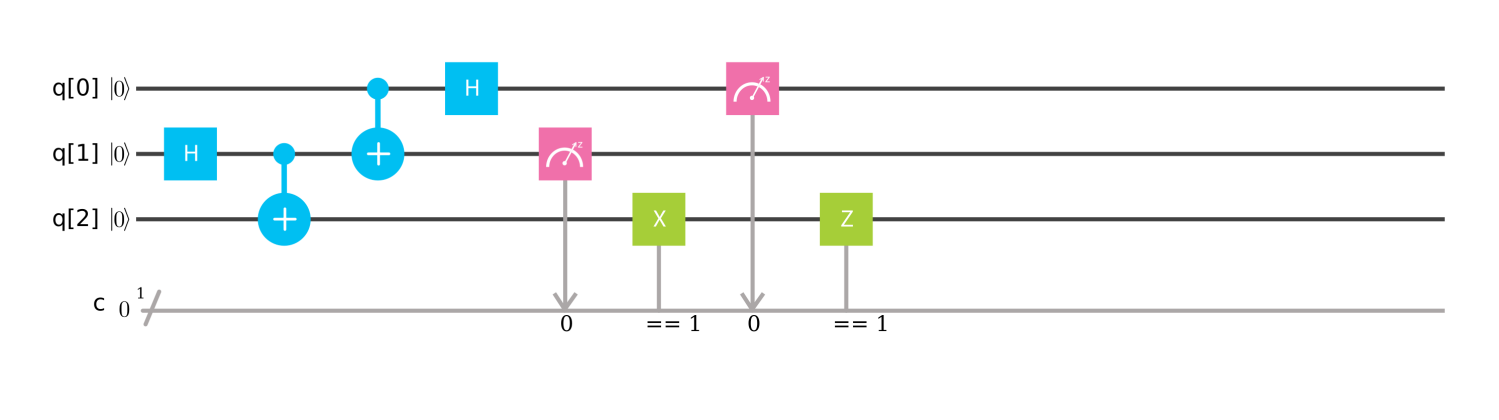
ちなみに今回の量子テレポーテーションを、IBM Qのシミュレータで実装すると次のようになります。
実機では、まだif文対応していないみたいですね。残念。
量子回路
OpenQASM
OPENQASM 2.0;
include "qelib1.inc";
qreg q[3];
creg c[1];
h q[1];
cx q[1],q[2];
cx q[0],q[1];
h q[0];
measure q[1] -> c[0];
if(c==1) x q[2];
measure q[0] -> c[0];
if(c==1) z q[2];