Unityに自前でイージング関数を用意する(C#)

Unityといえば、豊富なアセットがあり、イージングも当然たくさんありますが、自分で用意していろいろカスタマイズして遊びたいなと思い、自前で用意してみました。ググってもC#のソースがそのまま置いてあることもなかったので、他の言語を参考にUnity用に書き直し、せっかくなので共有しようと思います。

参考にしたサイトはこちら
https://easings.net/ja

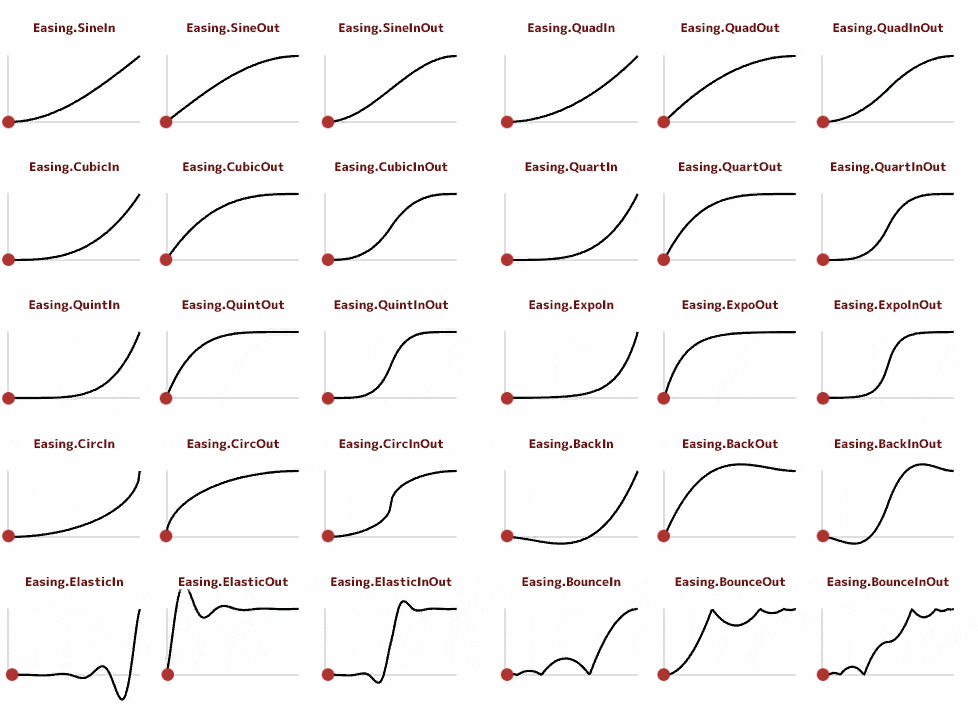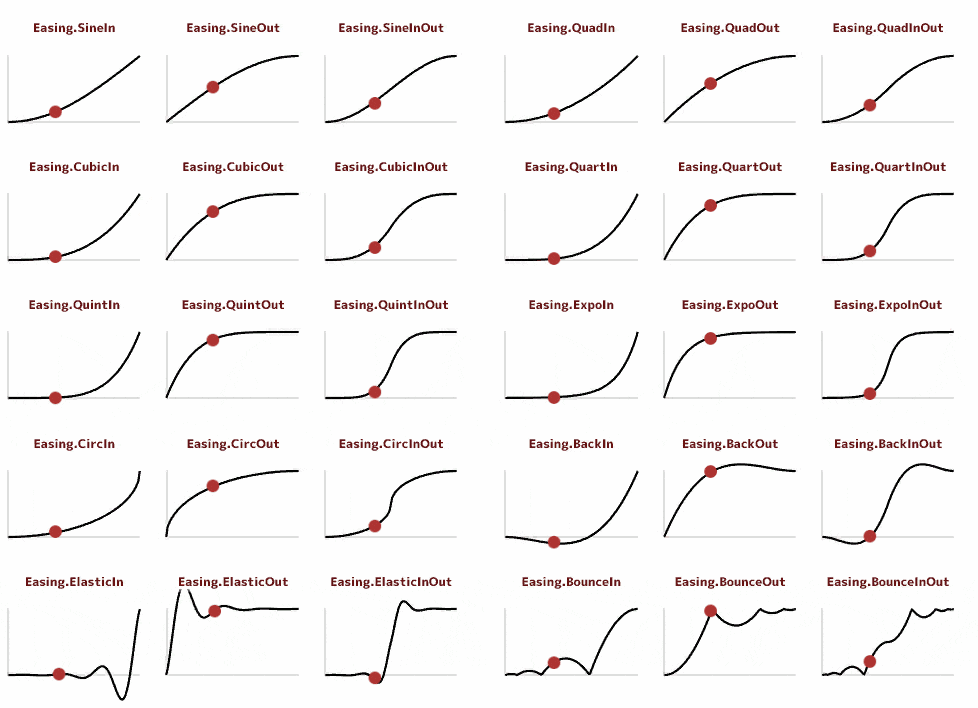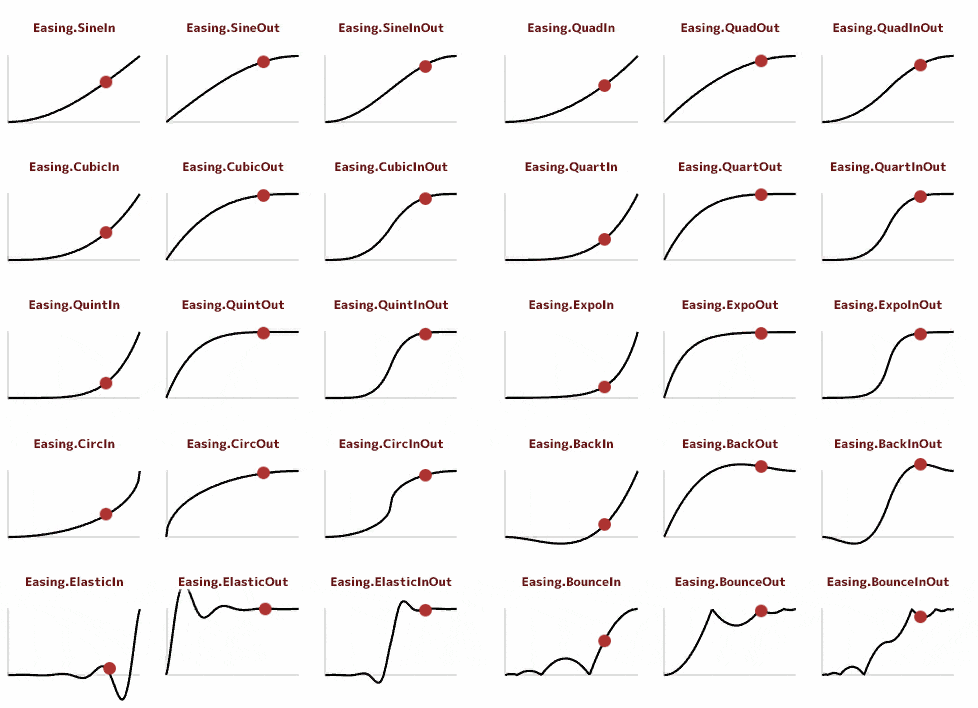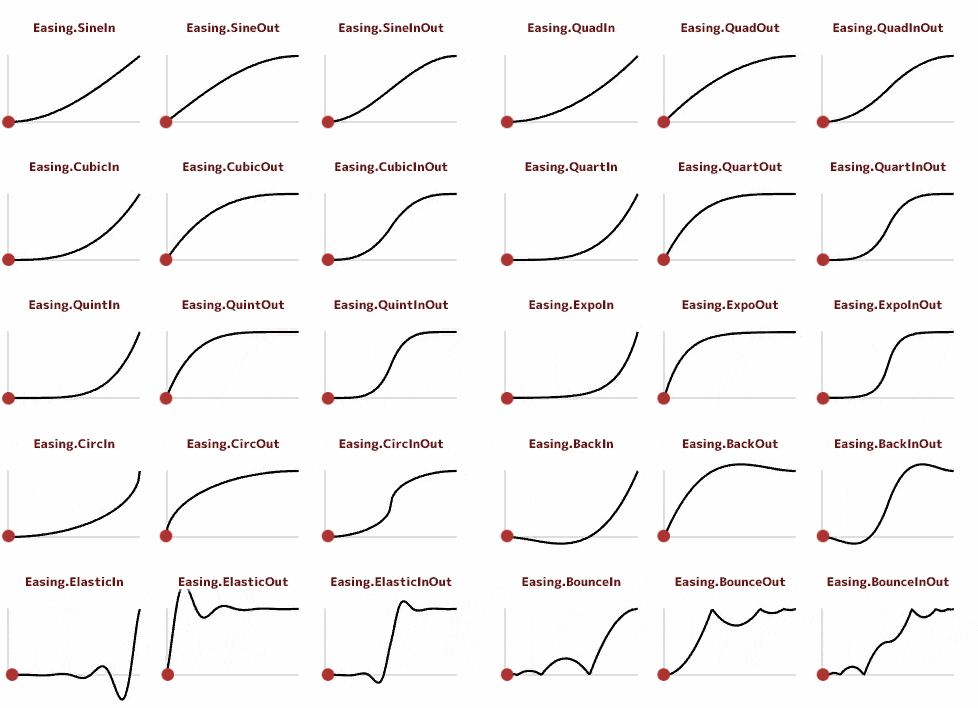
ここでは一部の紹介にとどめますが、全31種類のソースはこちらに置いておきます。
https://github.com/pixelflag/EasingTest

Unityでの動作イメージ

ちょっとずれているのは、画像の上にボールを乗っけてるだけだからです。これで勘弁してください。

一般的なイージングではありますが、簡単に説明しておきます。

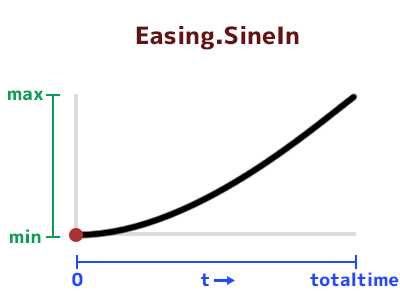
サンプルの動画のグラフは参考ページと同じものなので、おなじみの形です。
tが進行度、totaltimeが目標の時間、minが開始値、maxが目標値として定義します。
ソースコードはこんな感じ。

using UnityEngine;

public class Easing
{
    public static float SineInOut(float t, float totaltime, float min, float max)
    {
        max -= min;
        return -max / 2 * (Mathf.Cos(t * Mathf.PI / totaltime) - 1) + min;
    }
}

変数名、自分なりに読みやすくしています。cとかbとかわかりにくいですから。本来は抽象的な言葉のほうが正解だと思います。いろいろな使い方に当てはまるので。
実行はこうですね。

y = Easing.SineInOut(time, totalTime, min, max);

あとは、Updateでtimeを加算していってあげれば良いです。
詳しくはGitHubのほうを見てください。

もちろんUnityなので、Vector2でも計算が可能です。

初期位置から、ターゲットに向かって座標(Vector2)をイージングさせています。
なにがおこっているか、よくわからない感じですが、動作はしていることは確認できると思います。

ソースコードは、Vector2用のクラスを用意しますが、中身は基本同じです。

public class Easing2D
{
    public static Vector2 SineInOut(float t, float totaltime, Vector2 min, Vector2 max)
    {
        max -= min;
        return -max / 2 * (Mathf.Cos(t * Mathf.PI / totaltime) - 1) + min;
    }
}

floatをVector2に差し替えるだけですね。（Elasticだけ難解だったので諦めました。）
実行も同じ。

Vector2 pos = Easing2D.SineInOut(time, totalTime, min, max);
transform.position = pos;

ちょっとしたものを作るとき、アセットも大げさだなというとき、ちょっとコピペして使うとちょうどいいかもしれないですね。