Firefox 57以降のバージョンや、Google Chromeをはじめ各種のChromiumベースのブラウザでは、アドオン開発に共通のAPIセットを使用します。タブバー上のタブを任意の位置に移動するAPIとしてはtabs.move()という機能があり、これを使うと、タブを何らかのルールに基づいて並べ替えるという事もできます。実際に、以下のような実装例もあります。
- Firefox Multi-Account Containers: コンテナごとにタブを並べ替える。
- Sort tabs advanced: URLなどの条件でタブを並べ替える。
このようなタブの並べ替え機能を実現する時に気をつけたいポイントとして、 いかにAPIの呼び出し回数を減らし、効率よく、且つ副作用が少なくなるようにするか? という点があります。
ソートアルゴリズムの効率とは別の話
「並べ替え」「効率」というキーワードでソートアルゴリズムの事を思い浮かべる人もいるのではないでしょうか。確かにそれと似ているのですが、実際にはこの話のポイントはそこにはありません。
確かに、ソート自体は前述の2つのアドオンでも行っており、
- バラバラの順番のタブをコンテナごとに整理する
- URLなどの条件でタブの順番を整理する
という処理はまさにソートそのものです。しかし、現代のJavaScript実行エンジンは充分に高速なため、余程まずいアルゴリズムでもない限りJavaScriptで実装されたソートの速度自体は実用上の問題となりにくいです。
それよりも、その後に行う 「実際のタブを移動して、算出された通りの順番に並べ替える」 という処理の方が影響度としては深刻です。「タブ」というUI要素を画面上で移動するのは、純粋なデータのソートに比べると遙かにコストが大きいため、数百・数千個といったオーダーのタブをすべて並べ替えるとなると相応の時間を要します。また、タブが移動されたという事はイベントとして他のアドオンにも通知され、その情報に基づいて様々な処理が行われ得ます1ので、そのコストも馬鹿になりません2。
タブの並べ替えには手間がかかる
実際の並べ替えの様子を図で見てみましょう。[i, h, c, d, e, f, g, b, a, j] という順番のタブを、[a, b, c, d, e, f, g, h, i, j] に並べ替えるとします。
ぱっと見で気付くと思いますが、これは a, b, h, i の4つを左右で入れ換えただけの物です。しかし、人間にとっては一目瞭然の事でも、プログラムにとっては自明な事ではありません(それを検出するのがまさにこの記事の本題なのですが、詳しくは後述します)。
最もナイーブな3実装としては、元の並び順からタブを1つづつ取り出していくやり方が考えられます。その場合、行われる操作は以下のようになります。
というわけで、この場合だと10個のタブの並べ替えに8回の移動が必要となりました。元のタブの並び順次第では、移動は最大で9回必要になります。
ちなみに、tabs.move()は第一引数にタブのidの配列を受け取ることができ、その場合、第一引数での並び順の通りにタブを並べ替えた上で指定の位置に移動するという挙動になります。そのため、
browser.tabs.move([a, b, c, d, e, f, g, h, i, j], { index: 0 });
とすれば、APIの呼び出し回数としては確かに1回だけで済ませる事もできます。ただ、これは内部的には
browser.tabs.move(a, { index: 0 });
browser.tabs.move(b, { index: 0 + 1 });
browser.tabs.move(c, { index: 0 + 2 });
browser.tabs.move(d, { index: 0 + 3 });
browser.tabs.move(e, { index: 0 + 4 });
browser.tabs.move(f, { index: 0 + 5 });
browser.tabs.move(g, { index: 0 + 6 });
browser.tabs.move(h, { index: 0 + 7 });
browser.tabs.move(i, { index: 0 + 8 });
browser.tabs.move(j, { index: 0 + 9 });
といった移動操作と同等に扱われるため、タブが実際に移動されるコストは変わらず、タブが移動された事を通知するイベントもその都度通知されます。
ソートと同時にタブを移動するのではどうか?
ここまではArray.prototype.sort()でソートした結果に従って、後からまとめてタブを並べ替えるという前提で説明していました。では、Array.prototype.sort()を使わずに独自にソートを実装し、その並べ替えの過程で同時にタブも移動する、という形にするのはどうでしょうか?
例えばこちらのクイックソートの実装の過程にtabs.move()を呼ぶ処理を追加すると、以下のようになります。
// 再帰によるクイックソートの実装
function quickSort(tabIds, startIndex, endIndex) {
const pivot = tabIds[Math.floor((startIndex + endIndex) / 2)];
let left = startIndex;
let right = endIndex;
while (true) {
while (tabIds[left] < pivot) {
left++;
}
while (pivot < tabIds[right]) {
right--;
}
if (right <= left)
break;
// 要素の移動時に、同じ移動操作をタブに対しても行う
browser.tabs.move(tabIds[left], { index: right });
browser.tabs.move(tabIds[right], { index: left });
const tmp = tabIds[left];
tabIds[left] = tabIds[right];
tabIds[right] = tmp;
left++;
right--;
}
if (startIndex < left - 1) {
quickSort(tabIds, startIndex, left - 1);
}
if (right + 1 < endIndex ){
quickSort(tabIds, right + 1, endIndex);
}
}
const tabs = await browser.tabs.query({windowId: 1 });
quickSort(tabs.map(tab => tab.id), 0, tabIds.length - 1);
先の [i, h, c, d, e, f, g, b, a, j] を [a, b, c, d, e, f, g, h, i, j] に並べ替えるという例で見てみると、
このように、今度は4回の移動だけで並べ替えが完了しました。先の場合に比べると2倍の高速化なので、これは有望そうに見えます。
……が、そう考えるのは早計です。この例で並べ替えが4回で終わったのは、部分配列の左右端から要素を見ていくというアルゴリズムが、左右の端に近い要素が入れ替わる形になっていた [i, h, c, d, e, f, g, b, a, j] という元の並び順に対して非常にうまく作用したからに過ぎません。例えば入れ替わった要素の位置が左右の端から遠い位置にある [c, d, i, h, e, b, a, f, g, j] のようなケースでは、
と、今度は12回も移動が発生してしまいます。クイックソートは場合によっては同じ要素を何度も移動する事になるため、タブの移動のコストが大きい事が問題となっている今回のような場面では、デメリットの方が大きくなり得るのです。
また、クイックソートには「ソート結果が安定でない」という性質もあります。各要素のソートに使う値がすべて異なっていれば並べ替え結果は安定しますが、Firefox Multi-Account Containersでの「タブのコンテナごとに整理する」というような場面では、同じグループの要素の順番がソートの度に入れ替わってしまうという事になります。このような場合は要素間の比較の仕方を工夫するか、別のソートアルゴリズムを使う必要があります。
どうやら、このアプローチでは一般的に効率よくタブを並べ替えるという事は難しいようです。一体どうすれば「人が目視でするように、可能な限り少ない移動回数で、タブを目的の順番に並べ替える」という事ができるのでしょうか。
diffのアルゴリズムを応用する
このような問題を解決するには、diffや編集距離といった考え方が鍵となります。
Unix系の環境に古くからあるdiffというコマンドを使うと、2つの入力の差を表示する事ができます。Gitなどのバージョン管理システムにおいてもgit diffのような形で間接的に機能を利用できるようになっているため、各コミットで行った変更点を見るために使った事がある人は多いでしょう。例えば、A = [a, b, c, d] と B = [a, c, d, b] という2つの配列があったとして、AとBの差分はdiffでは以下のように表されます。
a
- b
c
d
+ b
行頭に-が付いている行は削除(AにはあってBには無い)、+が付いている行は追加(Aには無くてBにはある)を意味していて、これを見れば、「Aのbを2番目から4番目に移動する」というたった1回の操作だけでAをBにできるという事が見て取れます。このような「最小の変更手順」を求めるのが、いわゆる「diffのアルゴリズム」です。
つまり、これを「タブの並べ替え」に当てはめて、 「現時点でのタブの並び順」と「期待される並び順」とを比較し、算出された差分の情報に則ってタブを実際に移動するようにすれば、最小の手間でタブを並べ替えられる というわけです。
JavaScriptでのdiffの実装
diffの実装というとdiffコマンドが真っ先に思い浮かぶ所ですが、diffをライブラリとして実装した物は各言語に存在しており、もちろんJavaScriptの実装もあります。以下はその一例です。
-
jsdiff:npmの
diffパッケージとして導入可能な物(3条項BSDライセンス) - 「ツリー型タブ」に内蔵されているdiff.js:Pythonでの実装をJavaScriptに移植した物(Python Software Foundation License)
diffのアルゴリズムをタブの並べ替えに使うには、こういったライブラリをプロダクトに組み込むのがよいでしょう。ただ、その際には以下の点に気をつける必要があります。
- ライブラリのライセンスが他の部分のライセンスと競合しない事。
- ライブラリの内部表現を機能として利用できる事。
- 入力として任意の要素の配列を受け受ける事。
ライセンスの事は当然として、内部表現が利用できるとはどういう事でしょうか。
前述の例の「行頭に-か+が付く」という表現は、git diffなどで目にする事の多い「Unified Diff」形式に見られる表記ですが、これはあくまで最終出力です。ライブラリ内部では、相当する情報を構造化された形式で持っている事が多いです。npmのdiffであるjsdiffの場合は以下の要領です。
[
{ count: 1, value: [a] }, // 共通の箇所
{ count: 1, value: [b], removed: true }, // 削除された箇所
{ count: 2, value: [c, d] }, // 共通の箇所
{ count: 1, value: [b], added: true } // 追加された箇所
]
先のテキストでの表現をパースしてこのような表現を組み立てる事もできますが、ライブラリの内部表現→出力結果のテキスト表現→内部表現風の表現 という無駄な変換をするよりは、素直に内部表現をそのまま使えた方が話が早いです。
また、ライブラリの入力形式には任意の配列を受け付ける物である方が望ましいです。文字列のみを入力として受け付けるライブラリでも使えなくはないのですが、内部ではどの実装も基本的に配列を使っています。こちらも、比較したい配列→ライブラリに与えるための文字列→内部表現の配列 という無駄な変換が必要の無い物を使いたい所です。
npmのdiffパッケージであるjsdiffは、これらの点で使い勝手が良いのでおすすめの実装と言えます。
diffのアルゴリズムを使ったタブの並べ替え
diffを使ってタブを並べ替えるには、「ソート前の配列」「ソート後の配列」に「作業中の状態を保持する配列」を加えた3つの配列を使います。
const tabs = await borwser.tabs.query({ currentWindow: true });
const beforeIds = tabs.map(tab => tab.id); // ソート前のタブのidの配列
const afterIds = tabs.sort(comparator)
.map(tab => tab.id); // ソート後のタブのidの配列
let currentIds = beforeIds.slice(0); // 現在の状態を保持する配列(ソート前の状態で初期化)
次に、ソート前後のタブのidの配列同士の差分を取り、その結果に従ってタブを移動していきます。
const differences = diff.diffArrays(beforeIds, afterIds);
for (const difference of differences) {
if (!difference.added) // 削除または共通の部分は無視する
continue;
// ここにタブの移動処理を書いていく
}
タブの移動による並べ替えという文脈では、「削除」の差分で操作されるタブは対応する「追加」の操作によっても操作されます。また、「なくなるタブ(=処理中に閉じなければいけないタブ)」は原則として存在しません。よって、差分情報のうち「共通」と「削除」は無視して、「追加」にあたる物のみを使用します。
「追加」の差分情報を検出したら、まずタブの移動先位置を計算します。tabs.move()はタブの位置をindexで指定する必要がありますが、この時のindexは以下の要領で求められます。
// 以下、forループ内の処理
// 移動するタブ(1個以上)
const movingIds = difference.value;
// 移動するタブ群の中の右端のタブを得る
const lastMovingId = movingIds[movingIds.length - 1];
// ソート後の配列の中で、移動するタブ群の右に来るタブの位置を得る
const nearestFollowingIndex = afterIds.indexOf(lastMovingId) + 1;
// 移動するタブ群がソート後の配列の最後に来るのでないなら、
// 移動するタブ群の右に来るタブのindexを、タブ群の最初のタブの移動先位置とする
let newIndex = nearestFollowingIndex < afterIds.length ? currentIds.indexOf(afterIds[nearestFollowingIndex]) : -1;
if (newIndex < 0)
newIndex = beforeIds.length;
// 移動するタブ群の左端のタブの現在のindexを調べる
const oldIndex = currentIds.indexOf(movingIds[0]);
// 現在の位置よりも右に移動する場合、移動先の位置を補正する
if (oldIndex < newIndex)
newIndex--;
タブ群の移動先の位置を求めたら、いよいよtabs.move()でタブを移動します。このAPIは第1引数にタブのidの配列を渡すと複数のタブを一度に指定位置に移動できるので、APIの呼び出し回数を減らすためにもそのようにします。
// 実際にタブを移動する
browser.tabs.move(movingIds, {
index: newIndex
});
// 現在の状態を保持する配列を、タブの移動後として期待される状態に合わせる
currentIds= currentIds.filter(id => !movingIds.includes(id));
currentIds.splice(newIndex, 0, ...movingIds);
タブの移動はAPIを介して非同期に行われますが、タブの移動指示そのものはまとめて一度にやってしまって構いません。むしろ、途中でtabs.move()の完了をawaitで待ったりすると、タブの並べ替えの最中に外部要因でタブが移動されてしまうリスクが増えるので、ここはバッチ的に同期処理で一気にやってしまうのが得策です。
ただしその際は、2回目以降のtabs.move()に指定するタブの移動後の位置として、前のtabs.move()の呼び出しで並べ替えが完了した後の位置を指定しなくてはならないという点に注意が必要です。そのため、ソート前後の配列とは別に「並べ替えが実施された後の状態」を保持する配列を別途用意しておき、それだけを更新しています。前述のコード中で「タブの現在の位置」を求める際に、tabs.Tabのindexを参照せずにこの配列内での要素の位置を使用していたのは、これが理由なのでした。
実際の並べ替えの様子を、最初と同じ例を使って見てみましょう。[i, h, c, d, e, f, g, b, a, j] を [a, b, c, d, e, f, g, h, i, j] に並べ替えるとします。初期状態は以下のようになります。
-
beforeIds: [i, h, c, d, e, f, g, b, a, j] -
afterIds: [a, b, c, d, e, f, g, h, i, j] -
currentIds: [i, h, c, d, e, f, g, b, a, j] - 実際のタブ: [i, h, c, d, e, f, g, b, a, j]
この時、beforeIdsとafterIdsを比較して得られる差分情報は以下の通りです。
// 実際にはvalueはタブのidの配列だが、分かりやすさのためにここではアルファベットで示す
[
{ count: 2, value: [i, h], removed: true },
{ count: 2, value: [a, b], added: true },
{ count: 5, value: [c, d, e, f, g] },
{ count: 2, value: [b, a], removed: true },
{ count: 2, value: [h, i], added: true },
{ count: 1, value: [j] }
]
前述した通り、ここで実際に使われる差分情報は「追加」にあたる以下の2つだけです。
{ count: 2, value: [a, b], added: true }{ count: 2, value: [h, i], added: true }
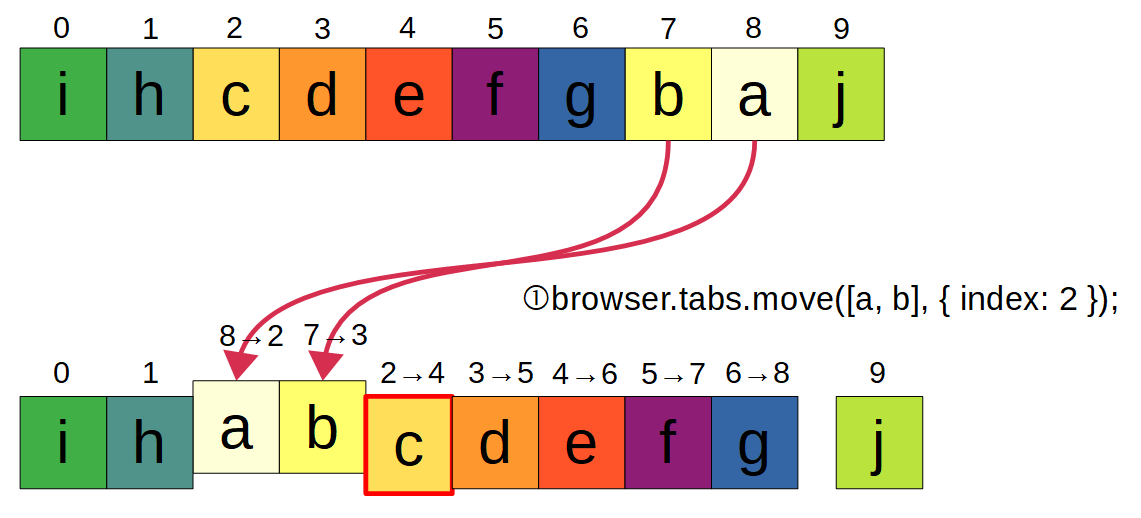
まず1つ目の差分情報に基づき、aとbを移動します。移動先の位置は、bの右隣に来る事になるタブ(=c)のcurrentIds内での位置ということで、2になります。
この時、b, aだった並び順も併せてa, bに並べ替えています。タブの移動完了後は、それに合わせる形でcurrentIdsも [i, h, a, b, c, d, e, f, g, j] へと更新します。
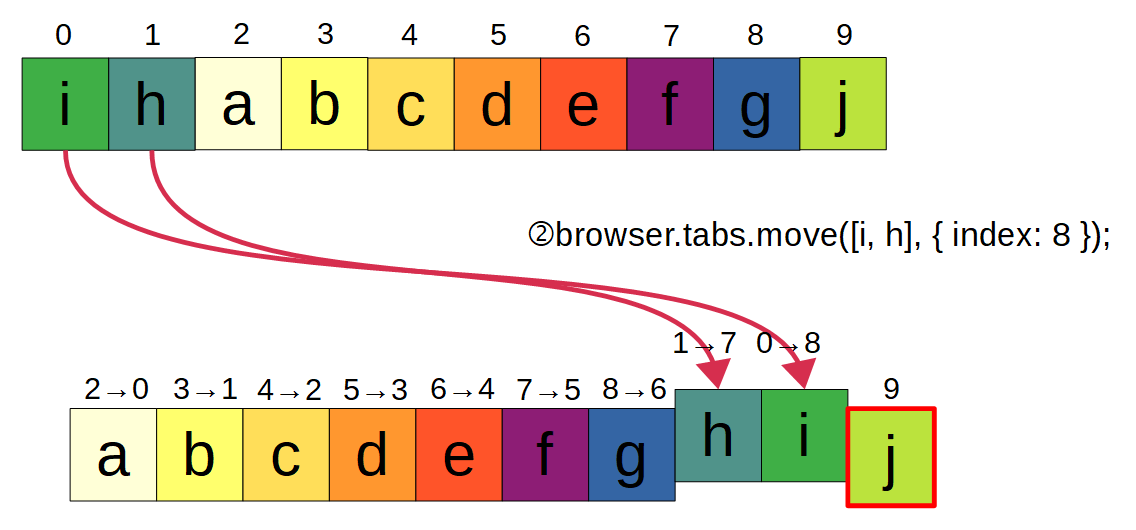
次は2つ目の差分情報に基づき、hとiを移動します。移動先の位置は、iの右隣に来る事になるタブ(=j)のcurrentIds内での位置から求めます。jの位置は9ですが、これはhの現在位置より右なので、そこから1減らした8が最終的な移動先位置になります。
この時も、i, hだった並び順をh, iに並べ替えています。タブの移動完了後は、それに合わせる形でcurrentIdsも [a, b, c, d, e, f, g, h, i, j] へと更新します。
ということで、APIの呼び出しとしては2回、タブの移動回数としては4回で並べ替えが完了しました。冒頭の例の8回に比べるとタブの移動回数は半分で済んでいます。
クイックソートでは却って移動回数が増えてしまった、[c, d, i, h, e, b, a, f, g, j] からの並べ替えではどうでしょうか。この場合、比較結果は以下のようになります。
[
{ count: 2, value: [a, b], added: true },
{ count: 2, value: [c, d] },
{ count: 2, value: [i, h], removed: true },
{ count: 2, value: [e] },
{ count: 2, value: [b, a], removed: true },
{ count: 2, value: [f, g] },
{ count: 2, value: [h, i], added: true },
{ count: 1, value: [j] }
]
前述の通り、このうち実際に使われる差分情報は以下の2つだけです。
{ count: 2, value: [a, b], added: true }{ count: 2, value: [h, i], added: true }
これは先の例と全く同じなので、APIの呼び出し回数は2回、実際のタブの移動は4回で済みます。
これらの例から、diffのアルゴリズムを用いると安定して少ない移動回数でタブを並べ替えられるという事が分かります。diffのアルゴリズムを用いた差分の計算自体はタブの移動に比べれば一瞬で済みますので、タブの移動回数を少なく抑えられれば充分に元が取れると言えるでしょう。
まとめ
以上、diffのアルゴリズムを用いてブラウザのタブを効率よく並べる方法について解説しました。
冒頭で例として挙げたタブの並べ替え機能を持つアドオンに対しては、以上の処理を実際に組み込むプルリクエストを既に作成済みです。
- Sort tabs with less steps by piroor · Pull Request #1377 · mozilla/multi-account-containers
- Sort tabs with less steps by piroor · Pull Request #2 · monomon/sort-tabs-advanced
これらの変更(およびこの記事)は、「ツリー型タブ」での内部的なタブの並び順に合わせてFirefoxのタブを並べ替える処理が元になっています。ツリー型タブではnpmのdiffとは別のdiff実装を使用していますが、diffの結果として得られる内部表現の形式はよく似ており、タブの並べ替え処理そのものは同じロジックである事が見て取れるはずです。
このように「最小の変更内容を計算して適用する」という考え方は、Reactで広まった仮想DOMという仕組みのベースとなっています。コンピューターが充分に高性能となり、富豪的プログラミングが一般化した現代においては、多少の事は力業で解決してしまって問題無い事が多いです。しかし、ネットワーク越しの処理や、携帯端末などデスクトップPCよりも性能が制限されがちな環境などで、何千・何万回といった単位で実行されるような処理にボトルネックがあると致命的な性能劣化に繋がりかねず、そのような場合には「コストの高い処理の実行頻度を減らしてトータルの性能を向上する」という正攻法での性能改善が依然として有効です。
なお、2者間で「変更箇所を検出する」というのは「共通部分を検出する」という事と表裏一体ですが、そのような計算は最長共通部分列問題と呼ばれ、diffのアルゴリズムの基礎となっています。どのような理屈で共通箇所を検出しているのか知りたい人は解説や論文を参照してみると良いでしょう。筆者は理解を諦めましたが……