Go to Qiita Advent Calendar 2024 Top
LoginSignup
1
4

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 3 years have passed since last update.

@piro87084806(piro)

R言語を初めて学んだのでまとめてみた

Posted at

データ分析/データ活用を行うための勉強の一環としてR言語を入門レベルで学んだので、情報を整理します。

前提条件

  • 記載例は、R及びRstudioをインストールしていることを前提としています
    R・RStudioをインストールしていない場合は、手順を記載したQiitaの記事がありましたので、参考ください

R言語とは(さっくり概要レベル)

  • 統計解析や機械学習などの応用統計に特化したプログラム言語
  • データ解析に優れているが、それ以外の機能を持っていない

R言語で出来ることの紹介

  • R言語で出来ることを、使われる用語と例を用いて記載します。

ベクトル

  • ベクトルの説明や、作り方・変数への代入方法や要素の抽出・追加などを整理します。

ベクトルの概要と作り方・変数への代入

  • ベクトルとは数字や文字列など、同じ型のデータをまとめたもの
  • ベクトルを作る際には、c()で要素を囲み、カンマ区切りで入力します。
■ベクトルの作り方の例
「1,2,3,4,5」という5つの数字の要素のベクトルを作成したい場合

c(1, 2, 3, 4, 5)
(実行結果)
[1] 1 2 3 4 5
  • ベクトルを変数に代入する場合は、変数名<-c(要素)と入力します。
■ベクトルを変数に代入する例
変数名：example
ベクトル要素：1,2,3,4,5

example <- c(1, 2, 3, 4, 5)
example

(実行結果)
[1] 1 2 3 4 5
  • ベクトルから要素を抽出・除外・追加する場合は、下記のような方法があります。
■変数exampleの2番目の要素を取り出す例
example <- c(1, 2, 3, 4, 5)
example[2]

(実行結果)
[1] 2

■変数exampleの1~3番目の要素を取り出す例
example <- c(1, 2, 3, 4, 5)
example[1:3]

(実行結果)
[1] 1 2 3

■変数exampleの3より大きい値を取り出す例
example <- c(1, 2, 3, 4, 5)
example[example>3]

(実行結果)
[1] 4 5
※example>3のみで実行した場合は、
[1] FALSE FALSE FALSE  TRUE  TRUE
という結果が返ってきます

■変数exampleの4番目の要素を除外する例
example <- c(1, 2, 3, 4, 5)
example[-4]

(実行結果)
[1] 1 2 3 5

■変数exampleに6を付け加えて、example2という変数に格納する例
example <- c(1, 2, 3, 4, 5)
example2 <- c(example, 6)
example2

(実行結果)
[1] 1 2 3 4 5 6

統計量を求める関数

  • 統計量を求める際に利用する関数を下記に整理します

Rで平均を出す

  • 平均とは、データの合計 割る データ数 で求められます
  • そのため、極端に大きな数字が入ってきた場合、それに引っ張られて平均値が増加してしまう可能性があります
  • Rで平均を出す場合は、mean(ベクトル) を使います
■Rで平均を出す例
example <- c(1, 2, 3, 4, 5, 100, 1000)
mean(example)

(実行結果)
[1] 159.2857

Rで中央値を出す

  • 中央値とは、データを昇順に並べた際の真ん中の値になります
  • そのため、平均と比べて極端に大きな数字があったとしてもそれに引っ張られない値が算出できます
  • Rで中央値を出す場合は、median(ベクトル) を使います
■Rで中央値を出す例
example <- c(1, 2, 3, 4, 5, 100, 1000)
median(example)

(実行結果)
[1] 4

Rで標準偏差を出す

  • 標準偏差とは、対象データのバラつきの大きさを示す指標であり、標準偏差が大きいほど、対象のデータに数値的な散らばりが多いことを表しています
  • Rで標準偏差を出す場合は、sd(ベクトル) を使います
■Rで標準偏差を出す例
example <- c(1, 2, 3, 4, 5, 100, 1000)
sd(example)

(実行結果)
[1] 372.4807

Rで相関係数を出す

  • 相関係数とは、2つの情報(今回はベクトル)に対して、どれほどの類似性があるかを、-1から+1の範囲で数字としてあらわしたものです
    -1に近ければ近いほど負の相関となり相関関係が少なく、+1に近ければ近いほど正の相関となり、相関関係があることがわかります
  • Rで相関係数を出す場合は、cor(ベクトル1, ベクトル2) を使います
  • 下記に1例として、7人のテストの点数と勉強時間の相関を例とします
    • テストの点数：70, 80, 40, 55, 95, 33, 63
    • 勉強時間(単位h)：10, 7, 2, 3, 12.5, 4, 8.3
■Rで相関係数を出す例(テストの点数をtest_scoreに、勉強時間をstudy_timeというベクトルにそれぞれ格納する)
test_score <- c(70, 80, 40, 55, 95, 33, 63)
study_time <- c(10, 7, 2, 3, 12.5, 4, 8.3)
cor(test_score, study_time)

(実行結果)
[1] 0.8524383

この例の結果は0.8以上だったので、勉強時間とテストの点数には正の相関があることがわかります。

Rによるブートストラップ法

  • Rでブートストラップ法を実現する方法を記載します
  • ここでのブートストラップ法とは、無数のデータが格納された母集団データから、サンプリングデータの抽出を何度も何度も繰り返してデータの標本を作成することで、そこから推定値を導き出し、母集団の傾向などを分析するための手法を指します
  • ここでは、ブートストラップ法を行う上で必要な、「サンプリング」と「繰り返し」について記載します

サンプリングの種類

  • サンプリングには、非復元抽出と復元抽出の2種類があります
  • 非復元抽出
    • 重複を許さないサンプリング方法。例えば、ある箱に10個のデータがあるとしたら、その中からデータを取り出したら箱には戻さずにサンプリングを続ける
  • 復元抽出
    • 重複を許すサンプリング方法。非復元抽出とは異なり、データを取り出したら出したデータを記録した後箱に戻す

Rでのサンプリング方法

  • Rでサンプリングをする場合は、sample(ベクトル, size = サンプル数, replace = TRUE or FALSE)を使います
■Rで1~9の連番から4つの数字を重複を許さずサンプリングする例(非復元抽出の例)
sample(c(1:9), size = 4, replace = FALSE)

(実行結果)
[1] 1 4 8 9

■Rで1~9の連番から4つの数字を重複を許してサンプリングする例(復元抽出の例)
sample(c(1:9), size = 4, replace = TRUE)

(実行結果)
[1] 4 6 9 9

■テストの点数を格納したtest_scoreというベクトルから非復元抽出で3つのデータをサンプリングし、sample_scoreというベクトルに格納する例
test_score <- c(70, 80, 40, 55, 95, 33, 63)
sample_score <- sample(test_score, size = 3, replace = FALSE)
sample_score

(実行結果)
[1] 55 33 63

Rの繰り返し処理の方法

  • 繰り返し処理を行いたい場合は、for文を使います
    for文の書き方は下記になります
■for文の書き方
for(繰り返し処理内で使う変数 in ベクトル){
  繰り返し処理したい内容
}

■test_scoreの中身をひとつずつ取り出し、print(画面に出力)する例
test_score <- c(70, 80, 40, 55, 95, 33, 63)
for(i in test_score){
  print(i)
}

(実行結果)
[1] 70
[1] 80
[1] 40
[1] 55
[1] 95
[1] 33
[1] 63

ブートストラップ法で分布を作成する

  • 下記のテストの点数と勉強時間を使って、ブートストラップ法で分布を作成します
    • テストの点数：70, 80, 40, 55, 95, 33, 63
    • 勉強時間(単位h)：10, 7, 2, 3, 12.5, 4, 8.3

ブートストラップ法で平均点の分布を作成する

  • 下記条件でテストの点数の平均値の分布を作成
    • 重複を許すサンプリング方法(復元抽出)を1000回繰り返す
    • サンプリングデータ数は7個
    • 平均値を格納するためにベクトルaverageを使う
■テストの点数の平均値の分布を作成する例
# 平均値を格納するために、空のベクトルaverageを作成
average <- c()
# テストの点数が入ったベクトルtest_scoreを作成
test_score <- c(70, 80, 40, 55, 95, 33, 63)
# 1000回繰り返す処理を作成
for(i in 1:1000) {
  # test_scoreから復元抽出で7つのデータをサンプリングし、sample_scoreというベクトルに格納する
  sample_score <- sample(test_score, size = 7, replace = TRUE)
  # meanを使って平均値を計算し、mというベクトルに格納する
  m <- mean(sample_score)
  # 計算結果をaverageに格納
  average <- c(average, m)
}
# averageに1000個分の平均値のデータが格納されていることを確認
print(average)
# 抽出した結果からヒストグラムを作成(例は下記に記載)
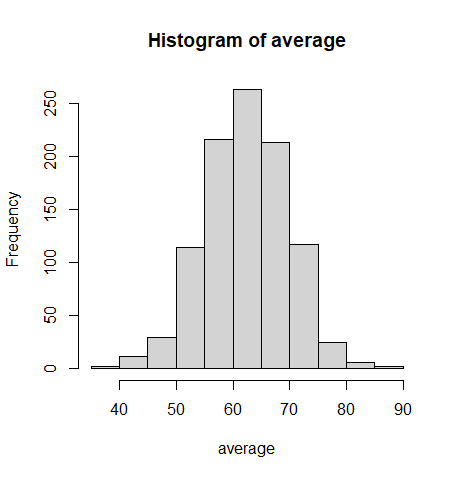
hist(average)

Histogram of average.png

  • ヒストグラムから、60～65点が平均値という傾向がわかります

ブートストラップ法で相関係数の分布を作成する

  • 下記条件でテストの点数と勉強時間の相関係数の分布を作成
    • 重複を許すサンプリング方法(復元抽出)を1000回繰り返す
    • サンプリングデータ数は7個
    • 相関係数を格納するためにベクトルcorrelation_coefficientを使う
■テストの点数と勉強時間の相関係数の分布を作成する例
# 相関係数を格納するために、空のベクトルcorrelation_coefficientを作成
correlation_coefficient <- c()
# テストの点数が入ったベクトルtest_scoreを作成
test_score <- c(70, 80, 40, 55, 95, 33, 63)
# 勉強時間が入ったベクトルstudy_timeを作成
study_time <- c(10, 7, 2, 3, 12.5, 4, 8.3)
# 1000回繰り返す処理を作成
for(i in 1:1000) {
  # 要素番号を重複を許してサンプリングし、ベクトルindexに格納
  index <- sample(1:length(test_score), size = 7, replace = TRUE)
  # サンプリングした要素番号を用いて、test_score・study_timeから要素を抽出
  score <- test_score[index]
  time <- study_time[index]
  # 抽出した要素を使って相関係数を算出
  tmp_cor <- cor(score, time)
  # 計算結果をcorrelation_coefficientに格納
  correlation_coefficient <- c(correlation_coefficient, tmp_cor)
}

# correlation_coefficientに1000個分の相関係数のデータが格納されていることを確認
print(correlation_coefficient)
# 抽出した結果からヒストグラムを作成(例は下記に記載)
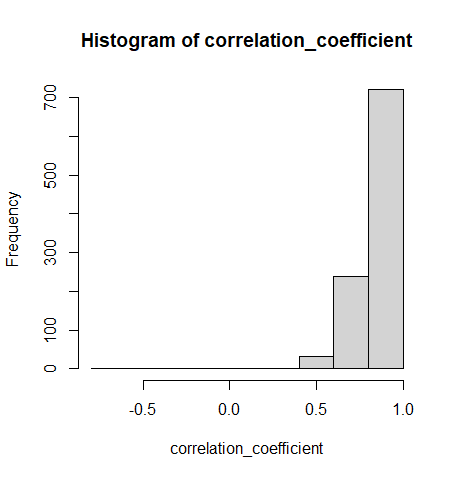
hist(correlation_coefficient)

Histogram of correlation_coefficient.png

  • ヒストグラムからかなり正の相関があることがわかります

その他グラフ例

  • Rで抽出可能な基本的なグラフを下記に記載します

棒グラフ

  • 棒グラフとは、棒の高さでデータの大小を表したグラフ
  • データの大小が、棒の高低で表されるので、データの大小を比較するのに適しています
  • Rで棒グラフを作成する場合は、下記のように記載します
    • 通常の棒グラフ：barplot(ベクトル)
    • 水平の棒グラフ：barplot(ベクトル, horiz = TRUE)

折れ線グラフ

  • 折れ線グラフとは、横軸に年や月などの時間を、縦軸にデータ量をとり、それぞれのデータを折れ線で結んだグラフ
  • 時間経過に伴うデータの推移や変化、増減等が一目で判断できます
  • Rで折れ線グラフを作成する場合は、下記のように記載します
    • plot(x軸ベクトル, Y軸ベクトル, type = "l")
      (type = "l(小文字のL)"を追加することで、各ポイントを線で結ぶように描画する)

ヒストグラム

  • ヒストグラムは、データの散らばり具合をみるのに使われます
  • 横軸にデータの階級を、縦軸にその階級に含まれるデータの数（人数、個数など）をとり、棒グラフで表します
  • Rでヒストグラムを作成する場合は、下記のように記載します
    • hist(ベクトル)

箱ひげ図

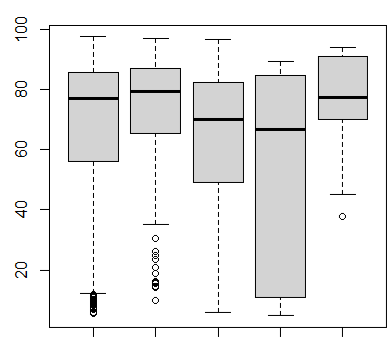
  • 箱ひげ図の例

box plot.png

  • 箱ひげ図とは四角い箱の上下に、ひげが生えている形をしているグラフです
  • ひげの一番下が最小値、真ん中の線が中央値、ひげの一番上が最大値を表しています
  • Rで箱ひげ図を作成する場合は、下記のように記載します
    • boxplot(y(連続変数)~x(カテゴリ変数), data = データ)

Rの関数の書き方

  • R言語もfunction()を使うことで共通的な処理を定義し、使いまわすことが出来ます
    関数は下記のように記載します
■テストの点数をx、回数をyとした際の、ブートストラップ法で平均値を求める関数の作成例
avg_function <- function(x, y) {
  # 平均値を格納するために、空のベクトルaverageを作成
  average <- c()
  # y回繰り返す処理を作成
  for(i in 1:y) {
    # test_scoreから復元抽出で7つのデータをサンプリングし、sample_scoreというベクトルに格納する
    sample_score <- sample(x, size = length(x), replace = TRUE)
    # meanを使って平均値を計算し、mというベクトルに格納する
    m <- mean(sample_score)
    # 計算結果をaverageに格納
    average <- c(average, m)
  }
  return(average)
}

# 作成した関数に直接の値で処理する場合
avg_function(x=c(70, 80, 40, 55, 95, 33, 63), y=1000)

# テストの点数が入ったベクトルtest_scoreを作成
test_score <- c(70, 80, 40, 55, 95, 33, 63)
# 作成した関数にベクトルの値を用いて処理する場合
avg_function(x=test_score, y=1000)

まとめ

これまでは数字を使ってグラフ作成というと、Excel一択であり、データ量やグラフなどExcelで作りづらい場合には四苦八苦していました。
ですが、今回R言語に触れてみたことで、データの扱いについては色々なやり方があるとことで視野が広がった気持ちでした。

今後は実用的な面で活用した事例なども書いていければと考えています。

最後まで見ていただき、ありがとうございました。

1
4
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
1
4

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?