進捗管理に使える確率・統計を python プログラムで理解する

問1

サイコロを100回振ったとき出目の合計はいくつになる？

平均・期待値

小学校で習う平均は統計量の筆頭です。まずは平均を用いてはじめの問の答えを導き、シミュレーション結果と照らし合わせてみます。

プログラム

import numpy as np
import numpy.random as rd
import matplotlib.pyplot as plt

# サイコロを定義する
#   平均が分かる
dice = [1, 2, 3, 4, 5, 6]
print("平均:", np.mean(dice))

# 試行回数を定義する
#   平均と組み合わせて合計の期待値が分かる
trialsNum = 100
print("合計の期待値:", np.mean(dice) * trialsNum)
input("続行するにはEnterキーを押してください . . .")

# 実際に試行する
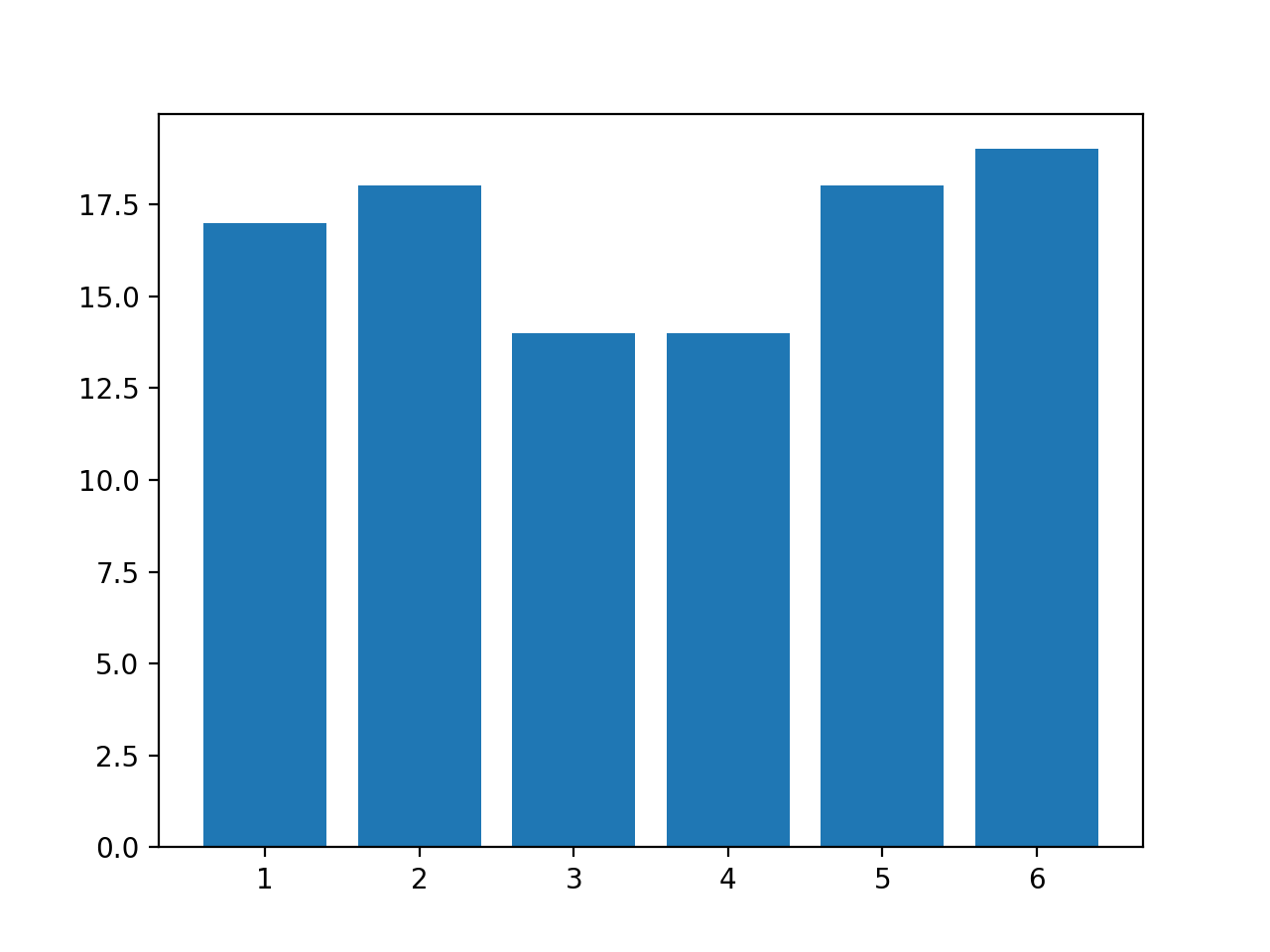
#   ヒストグラムを描画して出目の分布を確認する
resultList = [rd.choice(dice) for i in range(trialsNum)]
plt.hist(resultList, bins=6, rwidth=0.8, range=(0.5, 6.5))
plt.show()

print("合計:", np.sum(resultList))

実行結果(例)

乱数を使うので結果は一定ではありません。

標本平均: 3.5
合計の期待値: 350.0
続行するにはEnterキーを押してください . . .

合計: 355

解説

サイコロを1回振ったとき出うる目の平均は 3.5 ですから、100回振った合計は平均の100倍の 350 くらい...とはじめの問に答えられます。平均・期待値を使うと下記のような進捗管理ができます。

1. リソース単位(人日など)あたりに消化したタスク量の平均(=進捗ペース)を過去の実績から求める
2. 期日までに使える残りのリソース量と進捗ペースを掛け算して、消化できるタスク量の期待値を求める
3. 期待値と期日までに消化しなければならない残りのタスク量を比較して進捗の良し悪しを判断する

しかし比較して判断するのは人間の経験と勘に任せて良いんでしょうか？バーンダウンチャートを使うと時系列の傾向を見て判断できますが経験と勘に頼ることに変わりはありません。

分散・標準偏差

350 くらい...とはじめの問に答えられます。

350 くらい...というのはどのくらい”350 くらい”なのでしょうか？それを表すのが分散・標準偏差です。まずは標本から標準偏差を求め、次にシミュレーション結果から標準偏差を求めて照らし合わせてみます。

プログラム

import numpy as np
import numpy.random as rd
import matplotlib.pyplot as plt

# サイコロを定義する
#   平均と分散が分かる
dice = [1, 2, 3, 4, 5, 6]
print("標本平均:", np.mean(dice))
print("標本分散:", np.var(dice))

# 試行回数を定義する
#   標本平均と組み合わせて合計の期待値が分かる
#   標本分散と組み合わせて合計の標準偏差を予想できる
trialsNum = 100
print("合計の期待値          :", np.mean(dice) * trialsNum)
print("合計の標準偏差（予想）:", np.sqrt(np.var(dice) * trialsNum))
input("続行するにはEnterキーを押してください . . .")

# 実際に試行する...を試行する
metaTrialsNum = 10000
resultList = [np.sum([rd.choice(dice) for i in range(trialsNum)])
              for i in range(metaTrialsNum)]
myMean = np.mean(resultList)
myStd = np.std(resultList)
print("合計の平均　　　　　　:", myMean)
print("合計の標準偏差（実際）:", myStd)

# 68–95–99.7則に当てはまるか確認する
win = [len([n for n in resultList if myMean - r * myStd <= n and n <= myMean + r * myStd]) /
       metaTrialsNum for r in range(1, 4)]
print(
    f'μ±σ : {myMean - 1 * myStd :.1f} ~ {myMean + 1 * myStd:.1f}: {win[0]:.2%}')
print(
    f'μ±2σ: {myMean - 2 * myStd :.1f} ~ {myMean + 2 * myStd:.1f}: {win[1]:.2%}')
print(
    f'μ±3σ: {myMean - 3 * myStd :.1f} ~ {myMean + 3 * myStd:.1f}: {win[2]:.2%}')

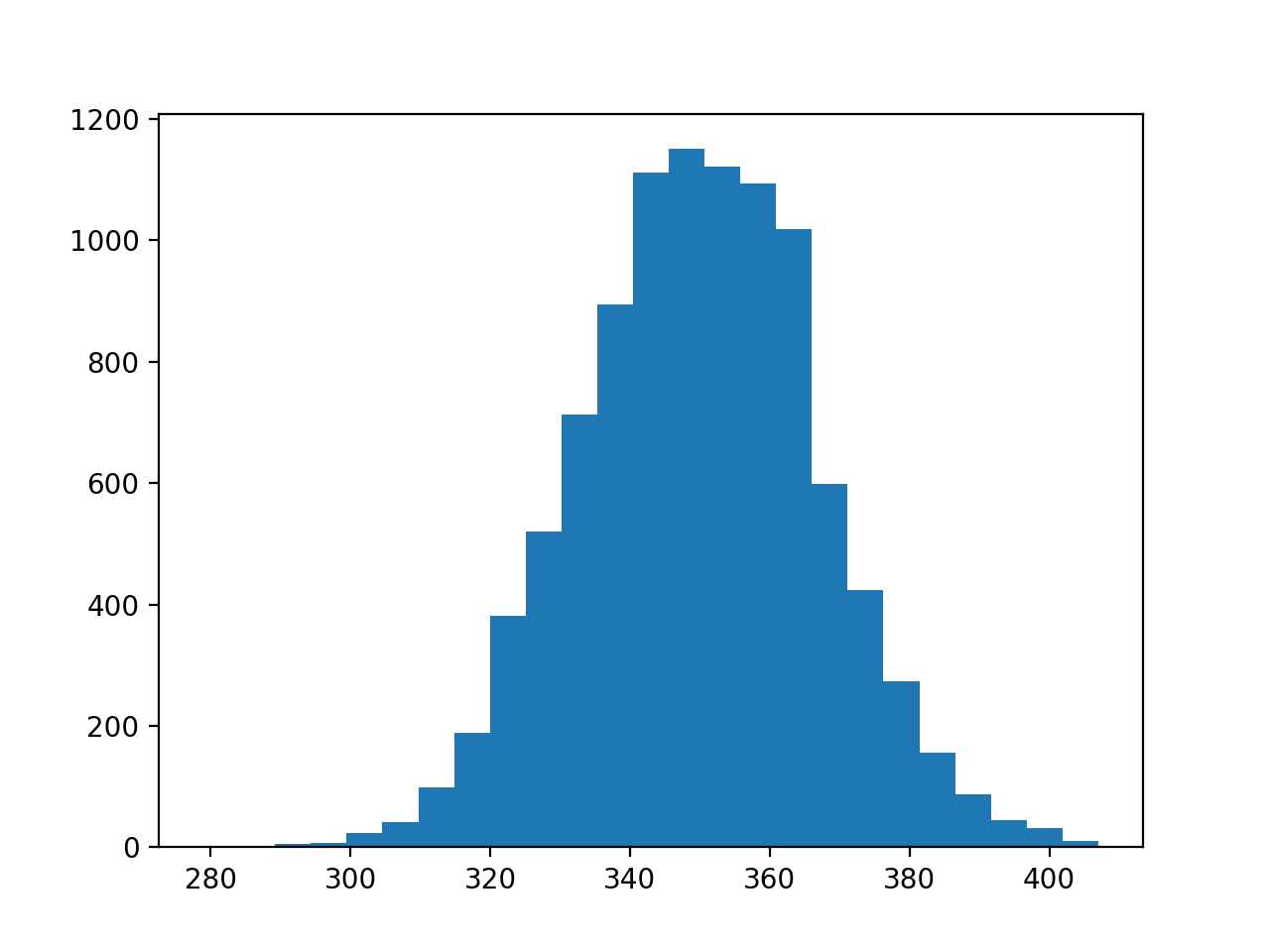
# ヒストグラムを描画して合計の分布を確認する
plt.hist(resultList, bins=25)
plt.show()

実行結果(例)

やはり乱数を使うので結果は一定ではありません。

標本平均: 3.5
標本分散: 2.9166666666666665
合計の期待値          : 350.0
合計の標準偏差（予想）: 17.078251276599328
続行するにはEnterキーを押してください . . .

合計の平均　　　　　　: 349.9814
合計の標準偏差（実際）: 17.034108548438923
μ±σ : 332.9 ~ 367.0: 69.69%
μ±2σ: 315.9 ~ 384.0: 95.77%
μ±3σ: 298.9 ~ 401.1: 99.76%

解説

合計の分布は 68–95–99.7則 へ綺麗に当てはまる正規分布となりました。約17となった標準偏差によって、どのくらい”350 くらい”なのかが表された訳です。そして標準偏差はシミュレーションせずとも標本から求めることができます。

誤差関数 erf

68–95–99.7則から μ±xσ の x が 1,2,3 の場合に試行結果がその範囲内である確率が分かりました。では x が 1.5 のときの確率などは分からないのでしょうか？あるいは出目の合計が 370 以上となる確率などは分らないのでしょうか？そこで誤差関数 erf の出番です。下記の python プログラムでこの関数の働きを図示してみます。

プログラム

import math
import numpy as np
import matplotlib.pyplot as plt

x = np.arange(-4.0, 4.1, 0.1)

leg1 = "μ-xσ ≦ a ≦ μ+xσ"
y1 = [math.erf(xi/math.sqrt(2)) for xi in x]
p1 = plt.plot(x, y1)

leg2 = "a ≦ μ+xσ"
y2 = [0.5 + 0.5 * math.erf(xi/math.sqrt(2)) for xi in x]
p2 = plt.plot(x, y2)

leg3 = "μ+xσ ≦ a"
y3 = [0.5 - 0.5 * math.erf(xi/math.sqrt(2)) for xi in x]
p3 = plt.plot(x, y3)

plt.legend((p1[0], p2[0], p3[0]),
           (leg1, leg2, leg3), loc=0)
plt.grid(True)
plt.show()

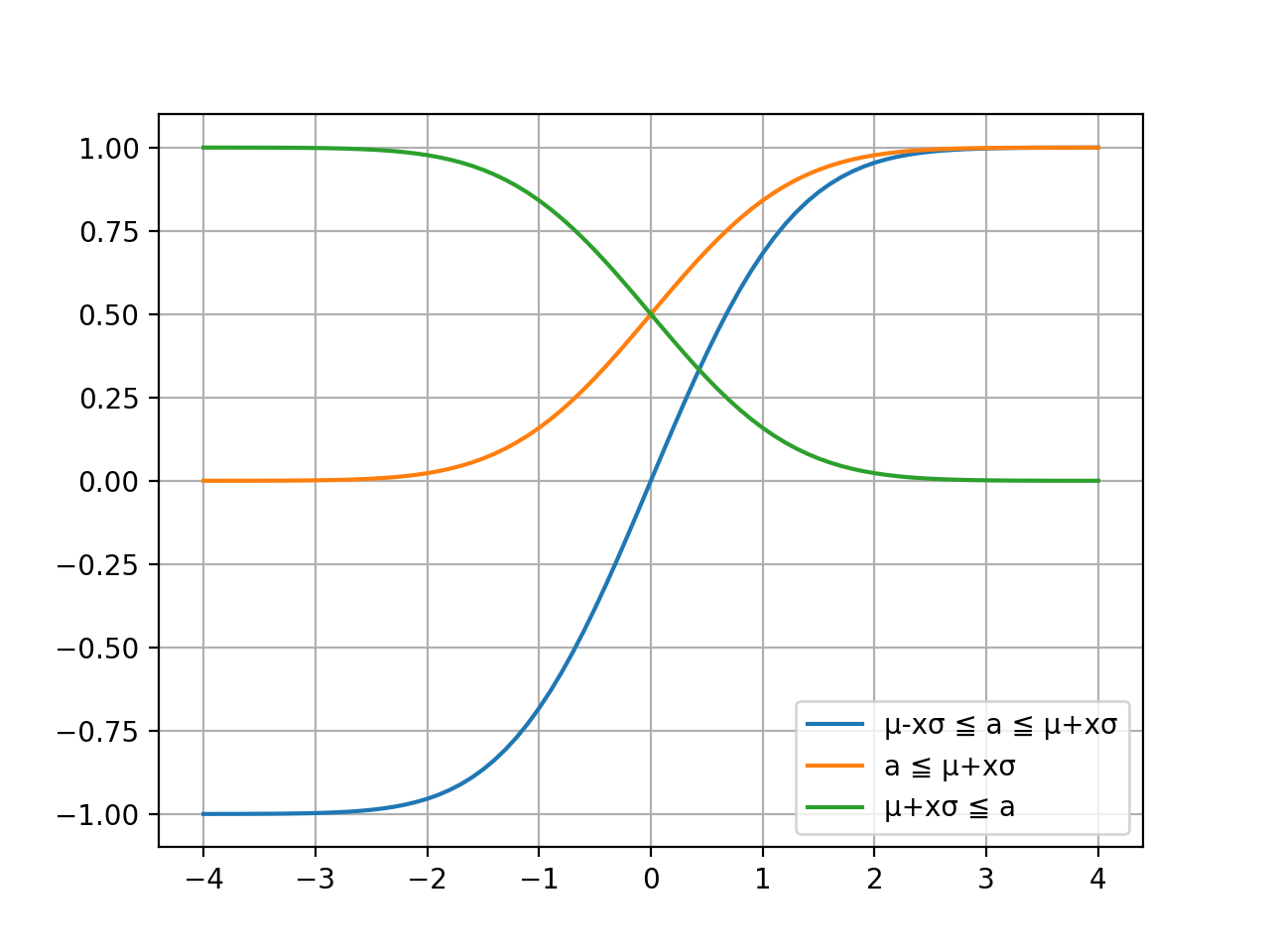
実行結果

解説

• 青色の線：試行結果 a が μ±xσ の範囲である確率を表します
• 橙色の線：試行結果 a が μ+xσ 以下である確率を表します
• 緑色の線：試行結果 a が μ+xσ 以上である確率を表します

誤差関数 erf により、任意の x について試行結果が μ±xσ 内である確率と μ+xσ 以下、あるいは以上である確率を計算できます。

あるいは出目の合計が 370 以上となる確率などは分らないのでしょうか？

誤差関数 erf を使い求めることができます
まずは次の式の μ と σ に値を当てはめて x の値を求めます。

μ+xσ = 370

合計の期待値 : 350.0
合計の標準偏差（予想）: 17.078251276599328

350+17x = 370
17x = 20
x = 1.18

そしてプログラムで使用した式の x に値を当てはめると確率が計算できます。

0.5 - 0.5 * math.erf(xi/math.sqrt(2))

0.5 - 0.5 * erf(1.18/√2) = 0.12 = 12%

サイコロを100回振ったとき出目の合計が 370 以上になる確率は約 12% です。平均、標準偏差、誤差関数により、はじめの問に対していろいろなことが答えられるようになりました。

問2

下表のペースで進んだチームはイテレーション20の完了時点でどこまで進む？

イテレーション	ベロシティ	累積
1	7	7
2	3	10
3	3	13
4	6	19
5	6	25

平均・期待値

μ = 100 ですね。

分散・標準偏差

イテレーション5までの分散は 3.5 であることからイテレーション20までの標準偏差は σ = √(3.5*20) ≒ 8.4 と予想できます。μ±3σの範囲はおよそ 75 ~ 125 となります。

誤差関数 erf

80% くらいの確度で答えるなら μ-1σ で 91 とでも言っときましょう(端数切り捨て)。イテレーション20までの進捗目標がそれより大きいなら目標を 91 まで下げるよう交渉すべきです。

99% の確度で答えるなら μ-3σ で 75 と言いましょう。逆を言えば目標が μ+3σ に相当する 125 だったら間に合う確率は 1% もありません。目標が 100 でも間に合う確率は 50% で五分五分の博打になります。「このまま平均通りのペースで進めば間に合うから順調だ！」なんて判断していると痛い目を見がちです。目標は 75 や 91 として、ストレッチゴールを 100 に設定するなどリスクに備えたムリのない計画を立てたいものです。

進捗の実績が貯まるごとに μ も σ も変動するので目標以上に進める確率を随時、誤差関数 erf で計算しましょう。サイコロと違って完璧な標本はないのですから。

なおリソース量の単位はイテレーション数とすると簡単ですが、より細かくしたい場合は日数や人日で計算することもできます。