線形回帰の一手法であるLasso回帰について、その数値解法であるISTAをJuliaで実装してみる記事です。数式を追いかけてコードにすることを主眼としているため、Juliaの実装については拙い箇所が多いと思います。間違い等あればご指摘いただけると幸いです。
線形回帰
回帰とは、連続値として得られたデータ(実験値)を想定したモデルに当てはめることです。線形回帰ではモデルとなる関数を線形関数とします。条件$x$(説明変数と言います)での実験から得られたデータを$y$とするとき、線形モデルは
$$ y = a x + b $$
であり、$a, b$がパラメータです。$x$に対して必ず真値yが得られるのであれば、モデルのパラメータを決定するためには$(x, y)$の組が2つあれば十分です。しかし、実験で得られるデータが必ず真値をとるということはあり得ず、誤差$\epsilon$が生じます。
$$ y' = ax + b + \epsilon $$
実験を適切に行なっていれば、誤差$\epsilon$は正規分布に従うホワイトノイズです。この誤差$\epsilon$がある限り、2組の$(y’, x)$からパラメータを決定することができません。そこでより多くの$(y’, x)$の組からパラメータを推定します(優決定系)。$\epsilon$は正規分布に従う確率変数なので、$y’$も確率変数です。確率変数からパラメータを推定するには、最も起こりやすい(尤もらしい)パラメータを採用します。これを最尤推定といいます。ここでは、$(y’, x)$とモデルの誤差の総量が最小になるものを尤もらしいとします。よって、
$$ E = (\mathbb{y}' - a\mathbb{x} - b)^2 = \sum_{i=1}^{m}(y'_i - ax_i - b)^2 $$
で定義されるEを最小にする$a, b$を求めればよいことになります。この方法を最小二乗回帰(OLS: Ordinary Least Square)と言います。いわゆる最小二乗法ですね。パラメータ$b$はモデル関数の切片ですが、データの前処理によって0にできるので、以降は$b$を常に0として考慮しません。
ここまでは確率変数$y’$に対して説明変数$x$は一つでしたが、説明変数が複数ある場合の回帰を重回帰と言います。データ数$m$, パラメータ数(説明変数の数)$n$としたとき、$y’$は$m$次元ベクトル$\mathbb{y}$、xは$m \times n$行列$X$、パラメータ$a$は$n$次元ベクトル$\mathbb{a}$となります。
$$ E = (\mathbb{y} - X\mathbb{a})^T(\mathbb{y} - X\mathbb{a}) = \sum_{i=1}^m (y_i - \sum_{j = 1}^n X_{ij}a_j)^2 $$
$E$は二乗の関数(かつ下に凸)ですので、パラメータ$a$での微分が0のとき最小値をとります。そのときの$a$が最尤パラメータです。
\begin{align}
E = (\mathbb{y} - X\mathbb{a})^T(\mathbb{y} - X\mathbb{a}) &= \mathbb{y}^T\mathbb{y} - 2\mathbb{a}^TX^T\mathbb{y} + \mathbb{a}X^TX\mathbb{a}
\\ \frac{\partial E}{\partial \mathbb{a}} &= -2X^T\mathbb{y} + 2X^TX\mathbb{a}
\\ a &= (X^TX)^{-1}X^T\mathbb{y}
\end{align}
正則化回帰
重回帰で複数の説明変数のパラメータを推定できると言いました。説明変数を増やすとモデル関数はより複雑になり表現能力が上がるので、実験データとの誤差が小さくなります。しかし、説明変数を増やしすぎると、実験データに過度にフィッティングしてしまい、モデル関数の意味をなさなくなります。これを過学習といいます。また、上記の式では$X^TX$の逆行列が出てきますが、$X^TX$が必ずしも正則であるとは限りません(極端に小さい固有値を持っている場合など)。そこで、正則化という方法を取ります。
正則化では先ほどの$E$に正則化項というものを加えます。正則化項を$a$のL1ノルム(絶対値の総和)とする回帰をLasso回帰、$a$のL2ノルム(二乗和)とする回帰をRidge回帰と言います。
Lasso回帰
$$ E = (\mathbb{y} - X\mathbb{a})^T(\mathbb{y} - X\mathbb{a}) + \lambda \sum_k |a_k| $$
Ridge回帰
$$ E = (\mathbb{y} - X\mathbb{a})^T(\mathbb{y} - X\mathbb{a}) + \sum_k \lambda a_k^2 $$
$\lambda$は正則化の度合いを決める正則化パラメータです。正則化項はモデル関数が複雑になると大きくなるので過学習を防ぐことができます。また、$X^TX$の対角成分を盛る効果があるため、$X^TX$を正則に近づけることができます。特にLassoでは寄与の小さい説明変数を間引く効果があり、スパースモデリングなどでも用いられます。
Lasso、Ridge回帰の解法
重回帰のときのように、正則化回帰でもaを計算しましょう。
Ridge回帰
同じようにaで微分して0の点を求めます。
\begin{align}
E &= (\mathbb{y} - X\mathbb{a})^T(\mathbb{y} - X\mathbb{a}) + \lambda \mathbb{a}^T\mathbb{a}
\\ &= \mathbb{y}^T\mathbb{y} - 2\mathbb{y}^TX\mathbb{a} + \mathbb{a}X^TX\mathbb{a} + \lambda \mathbb{a}^T\mathbb{a}
\\ \frac{\partial E}{\partial a} &= -2\mathbb{y}^TX + 2X^TX\mathbb{a} + 2\lambda \mathbb{a} = 0
\\ a &= (X^TX + \lambda I)^{-1}X^T\mathbb{y}
\end{align}
先の重回帰の式$a = (X^TX)^{-1}X^Ty$と比較すると、正則化項が$X^TX$の対角成分を盛っていることがよくわかります。
Lasso回帰
Lassoでも同様に、といきたいところですが、正則化項に含まれるL1ノルムは絶対値をとるため微分できません。一旦、問題を簡単にして考え直してみましょう。
単純な場合として以下を考えます。
$$ \min_a{(y - a)^2+\lambda|a|} $$
ここで$y, x$はベクトルでなく一つの変数とします。この場合、絶対値を場合分けすることで解くことができます。
$a \geq 0$のとき$|a| = a$なので
\begin{align}
(y - a)^2 + \lambda a &= y^2 - 2ya + a^2 + \lambda a
\\ &= y^2 + a^2 -2a(y - \frac{1}{2}\lambda)
\\ &= y^2 + (a - (y - \frac{1}{2}\lambda))^2 -(y - \frac{1}{2}\lambda)^2
\\ &=(a -(y-\frac{1}{2}\lambda))^2 + y\lambda - \frac{1}{4}\lambda^2
\end{align}
ここで、$(a - (y - \frac{1}{2}\lambda))^2 \geq 0$, $y\lambda - \frac{1}{4}\lambda^2 = const.$より、
$y - \frac{1}{2}\lambda \geq 0$のとき、$a = y - \frac{1}{2}\lambda$で最小値$y\lambda - \frac{1}{4}\lambda^2$をとる。
$y - \frac{1}{2}\lambda < 0$のとき、$a = 0$で最小値$y^2$をとる。
$a < 0$のとき$|a| = -a$なので
\begin{align}
(y - a)^2 - \lambda x &= y^2 - 2ay + a^2 -\lambda x
\\ &= y^2 + a^2 - 2a(y + \frac{1}{2}\lambda)
\\ &= y^2 + (a - (y + \frac{1}{2}\lambda))^2 - (y+\frac{1}{2}\lambda)^2
\\ &= (a - (y + \frac{1}{2}\lambda))^2 - y\lambda - \frac{1}{4}\lambda^2
\end{align}
同様に
$y + \frac{1}{2}\lambda \geq 0$のとき、$a = y + \frac{1}{2}\lambda$で最小値$-y\lambda - \frac{1}{4}\lambda^2$をとる。
$y-\frac{1}{2}\lambda < 0$のとき、$a = 0$で最小値$y^2$をとる。
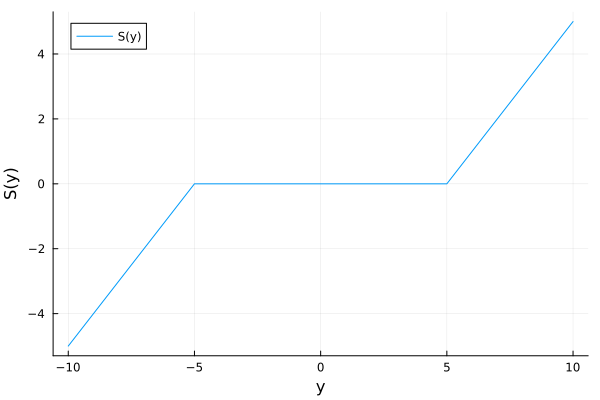
これらの場合分けをまとめて、yからaを求める関数$x = S_{\lambda}(y)$をつくってみると、
a = S_{\lambda}(y) = \left \{\begin{array}{ll} y - \frac{1}{2}\lambda & (y \geq \frac{1}{2}\lambda) \\ 0 & (-\frac{1}{2}\lambda < y < \frac{1}{2}\lambda)\\ y + \frac{1}{2}\lambda & (y \leq -\frac{1}{2}\lambda) \end{array} \right.
となります。この関数を軟判定しきい値関数(Soft Thresholding Function)と言います。場合分けの条件に1/2が入っていると面倒なので、$\lambda \rightarrow 2\lambda$として置き換えます。
a = S_{\lambda}(y) = \left \{\begin{array}{ll} y - \lambda & (y \geq \lambda) \\ 0 & (-\lambda < y < \lambda)\\ y + \lambda & (y \leq -\lambda) \end{array} \right.
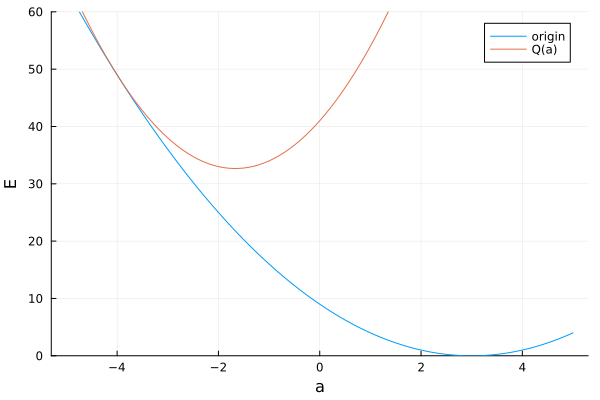
軟判定しきい値関数をグラフにすると以下のような形になっています($\lambda = 5$)。
以上、単純にした問題では場合分けで解けることが分かりましたが、本来解きたいのは
$$ \min_\mathbb{a}{(\mathbb{y} - X\mathbb{a})^2 + \lambda |\mathbb{a}|} $$
です。この問題を解くための、メジャライザー最小化(Majorize-Minimization)を紹介します。
メジャライザー最小化
メジャライザー最小化では最小化したい関数を上から抑える別の関数(メジャライザー)を考え、メジャライザーを逐次的に小さくしながら元の関数を最小化します。
まず、$(\mathbb{y} - X\mathbb{a})^2$の部分について考えます。この部分は二乗の関数なので、下に凸の放物線です。そこで、$(\mathbb{y} - X\mathbb{a})^2$を$\mathbb{a}_k$の周りでテイラー展開します。この$\mathbb{a}_k$は$\mathbb{a}$のk番目の要素ではなく、k回目の繰り返しのパラメータベクトルです。
$$ (\mathbb{y} - X\mathbb{a})^2 \simeq (\mathbb{y} - X\mathbb{a}_k)^2 -2X^T(\mathbb{y} - X\mathbb{a}_k)(\mathbb{a} - \mathbb{a}_k)+(\mathbb{a} - \mathbb{a}_k)^TX^TX(\mathbb{a}-\mathbb{a}_k) $$
これを上から抑えるようなメジャライザーを作るために、第3項をちょっと変えた
$$ Q(\mathbb{a}) = (\mathbb{y} - X\mathbb{a})^2 - 2X^T(\mathbb{y} - X\mathbb{a}_k)(\mathbb{a} - \mathbb{a}_k) + (\mathbb{a}- \mathbb{a}_k)L(\mathbb{a}-\mathbb{a}_k) $$
というものを考えます。第3項の$X^TX$を$L$に変えています。$Q(a)$は$\mathbb{a}_k$点での値と傾きが元の関数と同じですが、放物線の広がりだけが異なります。放物線の広がりを元の関数よりシャープにしてやると、全ての点で元の関数を上回る$Q(a)$を作れます。これをメジャライザーとします。
また、$L$は$X^TX$の固有値より大きければよく、$L$が大きいとそれだけ放物線がシャープになります。$L$を見積もるには、行列の固有値の性質を利用して
$$ \max\left\{\sum|X^TX|\right\} = L $$
とします。
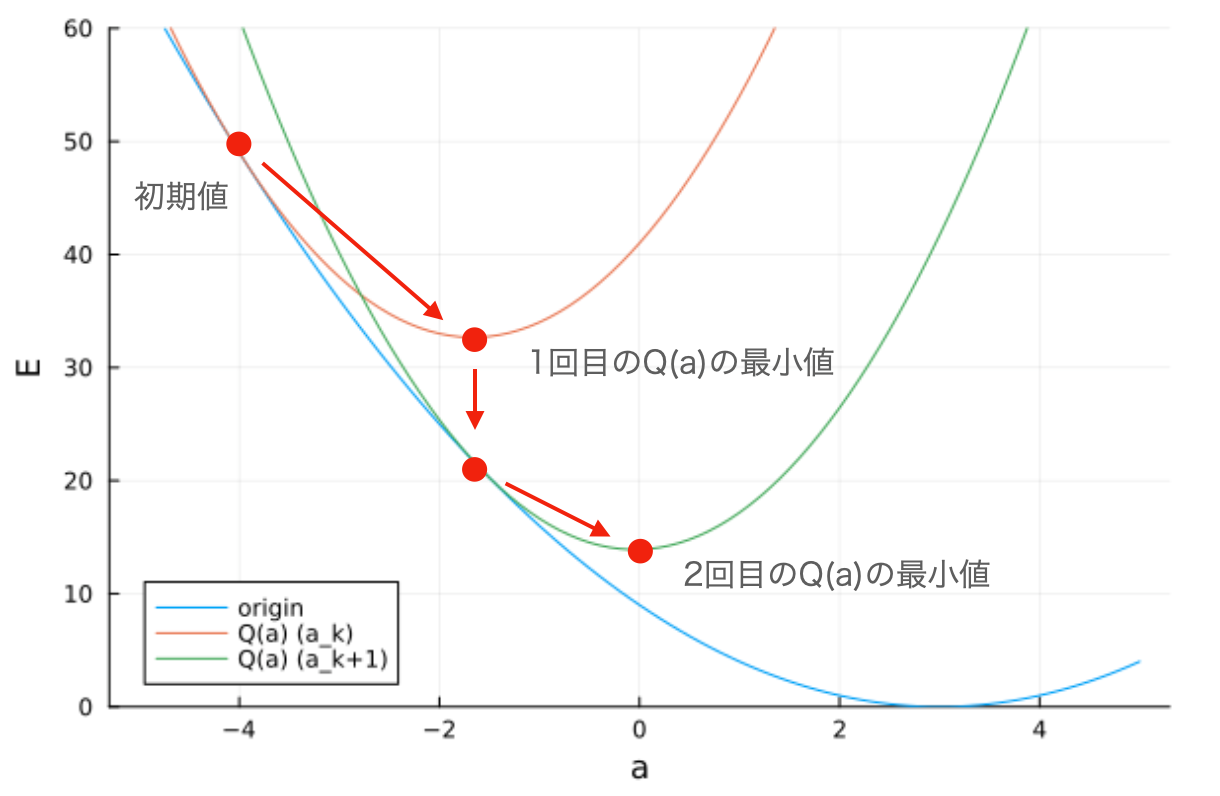
下図にメジャライザーの例と元関数のプロットを示します($a_k = -4$)。
メジャライザーについて最小の$\mathbb{a}$を求め、それを$\mathbb{a}_{k+1}$として新しいメジャライザーを作成します。まず$Q(a)$を変形します。
\begin{align}
Q(\mathbb{a}) &= (\mathbb{y} - X\mathbb{a}_k)^2 - 2X^T(\mathbb{y} - X\mathbb{a}_k)(\mathbb{a} - \mathbb{a}_k) + L(\mathbb{a} - \mathbb{a}_k)^2
\\ &= L\left \{\frac{1}{L}(\mathbb{y} - X\mathbb{a}_k)^2 - \frac{2}{L}X^T(\mathbb{y} - X\mathbb{a}_k)(\mathbb{a}-\mathbb{a}_k) + L(\mathbb{a}-\mathbb{a}_k)^2\right\}
\\ &= L\left \{\frac{1}{L}(\mathbb{y} - X\mathbb{a}_k)^2 + (\mathbb{a}-\mathbb{a}_k - \frac{1}{L}X^T(\mathbb{y} - X\mathbb{a}_k))^2 - \frac{1}{L}X^TX(\mathbb{y} - X\mathbb{a}_k)^2\right \}
\\ &= L\left(\mathbb{a} - \mathbb{a}_k - \frac{1}{L}X^T(\mathbb{y}-X\mathbb{a}_k)\right)^2 + (\mathbb{y}-X\mathbb{a}_k)^2 - \frac{1}{L}X^TX(\mathbb{y} - X\mathbb{a}_k)^2
\end{align}
この第2項以降は$\mathbb{a}$を含まない定数であるため、最小化では第1項のみ考えればよいです。
元々の関数の$(\mathbb{y} - X\mathbb{a})$をメジャライザーで置き換えると
$$ \min_\mathbb{a}\left\{L\left(\mathbb{a}-\mathbb{a}_k - \frac{1}{L}X^T(\mathbb{y}-X\mathbb{a}_k)\right)^2 + \lambda|\mathbb{a}|\right\} $$
となります。2乗の項中の$-\mathbb{a}_k - \frac{1}{L}X^T(\mathbb{y}-X\mathbb{a}_k)$の部分は$\mathbb{a}$に関係しないので
$$ v = \mathbb{a}_k + \frac{1}{L}X^T(\mathbb{y} - X\mathbb{a}_k) $$
と置いて
$$ \min_\mathbb{a}\left\{L(\mathbb{a}-v)^2 + \lambda|\mathbb{a}|\right\} $$
とすると、先に説明した軟判定しきい値関数での場合分けを用いることができます。
この最小化で求められる$\mathbb{a}$を$\mathbb{a}_k+1$として、新たにメジャライザーを定義すると、その最小値は元の関数の最小点に近づきます。
ちなみに、$v$は$\mathbb{a}_k$を勾配$X^T(\mathbb{y} - X\mathbb{a}_k)$の方向に修正する形になっています。勾配法における更新式とも取れますね。
これを繰り返すことで元の関数の最小値を求めます。
一連の手順をまとめると
\left \{ \begin{array}{ll} v = \mathbb{a}_k + \frac{1}{L}X^T(\mathbb{y} - X\mathbb{a}_k) \\ \mathbb{a}_{k+1} = S_{\lambda}(v) \end{array} \right.
という漸化式が得られます。この手法をISTA(Iterative Shrinkage soft-Thresholding Algorithm)と言います。
Juliaでの実装
ここまで長かったですが、Juliaでの実装自体は単純です。
まず軟判定しきい値関数を作ります。
function soft_th(v, λ)
if (v > λ)
r = v - λ
elseif (v < -λ)
r = v + λ
else
r = 0
end
return r
end #soft_th
ISTAを実行する関数は以下です。このコードでは収束の判定はせず指定回数を繰り返しています。
function majorize_minimization(X, y, ω, λ, iter)
m, n = size(X)
for i = 1:iter
for j = 1:n
X_j = X[:, j]
v = ω[j] + (X_j ⋅ (y .- X*ω))/sum(X_j.^2)
ω[j] = soft_th(v, λ)
end
end
return ω
end #majorize_minimization
例としてbostonhousingのデータをLasso回帰してみましょう(bostonhousingはもうsklearnのデータセットに入ってないらしいですが)。
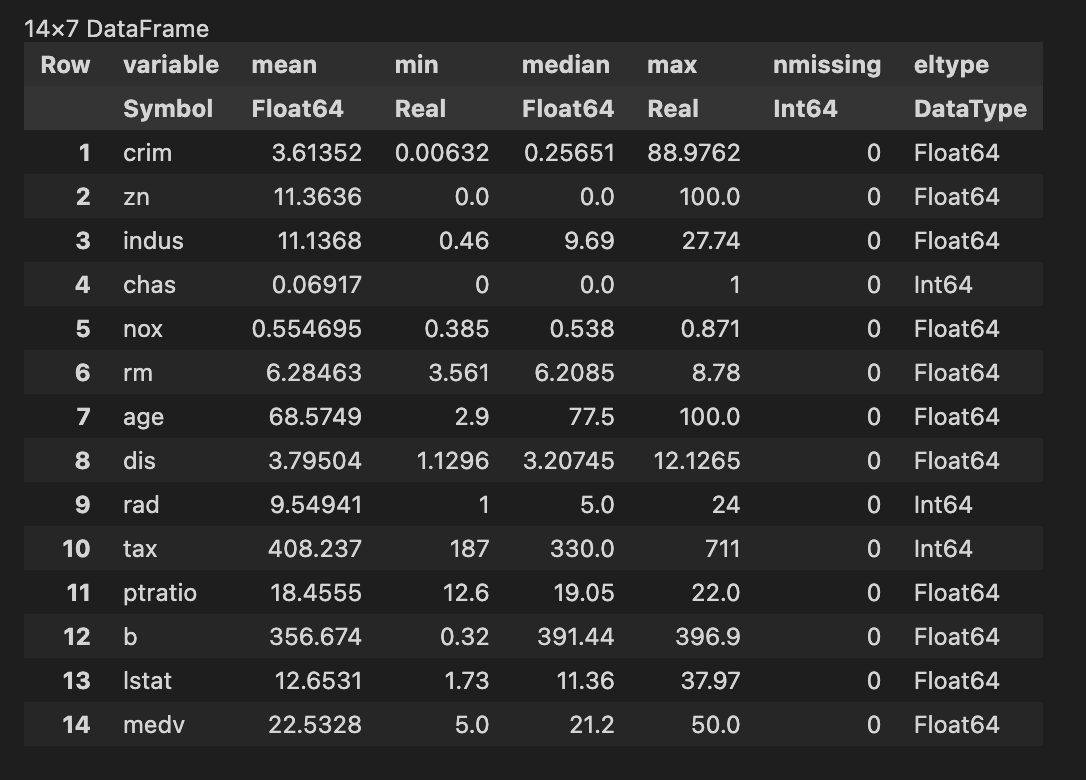
回帰をする前にbostonhousingデータの統計値を見てみましょう。JuliaにはDataframeのライブラリがあるので便利ですね。
using DataFrames
using CSV
bostonhousing = CSV.read("./bostonhousing.csv", DataFrame)
describe(bostonhousing)
meanの列を見ると、平均値が0ではない変数が多いですね。回帰分析で引いた直線はデータの重心$(\bar{y}, \bar{x})$を必ず通るので、平均値が0でない変数がある場合、切片が0になりません。ISTAの実施には切片があると面倒なので、切片を0にする前処理を行います。
ちなみに、今回の目的変数($y$)はmedv(住宅価格)です。
y = bostonhousing[:, "medv"]
y = y .- describe(bostonhousing)[14, 2]
bostonhousing = select(bostonhousing, Not(:medv))
m ,n = size(bostonhousing)
X = Matrix(bostonhousing)
for i = 1:n
X[:, i] = X[:, i] .- describe(bostonhousing)[i, 2]
end
Lasso回帰をします。本来は正則化係数$\lambda$をクロスバリデーションなどで決定するのですが、ここでは$\lambda$を変化させてLassoによる説明変数の削減の様子を見てみます。
init_a = ones(size(X)[2])
a_list = Vector(undef, size(X)[2])
λ = exp10.(LinRange(0, 4, 300))/100
iter = 100
for l in λ
ω = majorizer_minimization(X, y, init_a, l, iter)
a_list = hcat(a_list, a)
end
a_list = a_list[:, 2:end]
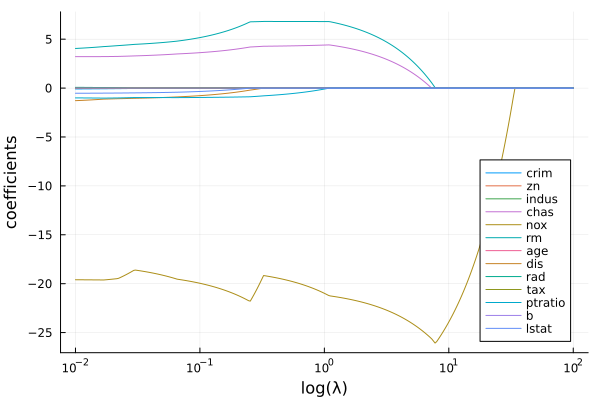
このa_listをplotすると以下のようになります。
(一部ちょっと変動が大きいですが)正則化係数を大きくすると説明変数が削減されているのがわかります。
まとめ
今回はLassoの最小化問題を解く手法であるISTAを導出してJuliaで実装しました。スパースモデリングなどに引っ張りだこなLassoですが、その裏側は思いの外簡単で、シンプルな漸化式で表せることが分かりました。
いずれ正則化係数$\lambda$を決定するクロスバリデーションや、モデルの評価のためのAICについてJuliaで実装してみたいと考えています。
参考文献
・http://www-adsys.sys.i.kyoto-u.ac.jp/mohzeki/Presentation/lectureslide20150902-3.pdf