有限要素法による二次元静弾性解析(Fortran)

　久々の投稿です。有限要素法による静弾性解析プログラムをFortranで書きます。静弾性解析とか機械工学については全くの門外漢なのですが、講義でやったのでまとめがてら書けたらと思います。コードはGitHub¹

#有限要素法
　多くの自然現象は微分方程式で記述できます。簡単な微分方程式なら境界条件の情報があれば頑張って解くことができますが、2階の偏微分方程式となるともはや解析的に解けなくなってきます。そのような微分方程式を強形式(Strong Form)といいます。
　解析的に解けない、あるいは解くのがとてもめんどくさいとするなら、厳密な解をあきらめて、近似解でもいいから解ける形式に変形して解きます。強形式を解けるような形(弱形式)にして、問題を解く領域を要素に分割し、要素ごとに弱形式を解く手法を有限要素法といいます。
　強形式から弱形式の変換の例を示しましょう。
$$\frac{d^2 u}{dx^2} + u^2 x + x^2 = 0, x\in[0, 1]$$
$u(x)$を未知関数として、境界条件
$x = 0$のとき$\frac{du}{dx} = 0$(Neumann条件)、$x = 1$のとき$u = 1$(Dirichlet条件)という問題を考えます。
　強形式→弱形式の変換でまず考えるのは、近似解にすることです。なので、右辺を0でなくある誤差$\epsilon$とします。
$\frac{d^2 u}{dx^2} + u^2 x + x^2 = \epsilon$
これを問題を考える領域全体で積分し、全体でどれぐらいずれるかを$I$として表すと、
$I = \int_0^1 w(x)\epsilon dx = \int_0^1 w(x)\left[\frac{d^2 u}{dx^2} + u^2 x + x^2\right]dx$

[ ]は$\epsilon$に上の式を代入したものです。$w(x)$は重み関数で、この重みを変化させて最小の$I$を目指します。

最適化の要領で$\frac{\partial I}{\partial w} = 0$となるところを探せばいいのです。

$I$の中でめんどくさいのが$w(x)\frac{d^2 u}{dx^2}$の項です。微分の順番を入れ替えてみて、

$\frac{d}{dx}(w\frac{du}{dx}) = \frac{dw}{dx}\frac{du}{dx} + w\frac{d^2 u}{dx^2}$
$w\frac{d^2 u}{dx^2}$は、

$w\frac{d^2 u}{dx^2} = \frac{d}{dx}(w\frac{du}{dx}) - \frac{dw}{dx}\frac{du}{dx}$

ちょっと変わった感じでしてますが要するに部分積分です。

$I = \int_0^1 {\frac{d}{dx}(w\frac{du}{dx}) - \frac{dw}{dx}\frac{du}{dx} + wu^2x + wx^2}dx = \left[w\frac{du}{dx}\right]_0^1 + \int_0^1 (-\frac{dw}{dx}\frac{du}{dx} + wu^2x + wx^2)dx$

境界条件から第一項は$\left[w\frac{du}{dx}\right]_0^1 = 0$になります。これで弱形式になりました。積分内の微分の次数が減っているのがわかると思います。
　ここで解を$u(x) = u_0 + u_1 x + u_2 x^2$の多項式と仮定します。重み関数も同じ形で$w(x) = w_0 + w_1x + w_2x^2$とします。重みのとり方などは有限要素法の中でも色々方法がありますが、今回は解と同じ形としました。$u(x)$, $w(x)$を$I$に代入して要素内で

$\frac{\partial I}{\partial w_0} = 0$, $\frac{\partial I}{\partial w_1} = 0$, $\frac{\partial I}{\partial w_2} = 0$となるような$u(x)$が解です。

#静弾性解析
　静弾性解析では、弾性の範囲内での物体のひずみを計算することで、物体に応力がかかったときにどうなるかを知ることができます。二次元の静弾性解析は以下の式からなります。

まず、ひずみの式

$\epsilon_x = \frac{\partial u}{\partial x}$, $\epsilon_y = \frac{\partial v}{\partial y}$, $\gamma_{xy} = \frac{\partial u}{\partial y} + \frac{\partial v}{\partial x}$

$\epsilon_x$, $\epsilon_y$: x方向, y方向の垂直ひずみ,　$\gamma_{xy}$: せん断ひずみ,　 $u$, $v$: x方向, y方向の変位

次に、応力とひずみの関係

$\epsilon_x = \frac{\sigma_x - \upsilon \sigma_y}{E}$, $\epsilon_y = \frac{\sigma_y - \upsilon \sigma_x}{E}$, $\gamma_{xy} = \frac{2(1+\upsilon)}{E}\tau_{xy}$

$\upsilon$: ポアソン比, $E$: 縦弾性係数,　 $\sigma_x$, $\sigma_y$: x方向, y方向の垂直応力,　$\tau_{xy}$: せん断応力
中学や高校でやったフックの法則ってやつです。

最後に、釣り合いの式

$\frac{\partial \sigma_x}{\partial x} + \frac{\partial \tau_{xy}}{\partial y} + X = 0$, $\frac{\partial \tau_{xy}}{\partial x} + \frac{\partial \sigma_y}{\partial y} + Y = 0$

$X$, $Y$: x方向, y方向の体積あたりに受ける力(重力とか)
なんか見た目が複雑そうですが運動方程式です。

式の数が多いですが、行列式でまとめることができます。まとめると、

$(\epsilon) = [L](u)$, $(\sigma) = [D](\epsilon )$, $[L]^{\mathrm{T}}(\sigma ) + {F} = (0)$
$[L]$とか$[D]$とかは上の関係をまとめたものです。
$[L] = \left[\begin{matrix} \partial/\partial x&0\
0&\partial/\partial y\
\partial/\partial y&\partial/\partial x\end{matrix}\right]$
$[D] = \frac{E}{1-\nu^2}\left[\begin{matrix} 1&\nu&0\
\nu&1&0\
0&0&(1-\nu)/2\end{matrix}\right]$
さて、式が出揃いましたので、有限要素法で解けるように変形しましょう。まず、そのままだとなにがめんどくさいのかと言うと、３つ目の釣り合いの式です。

x方向とy方向をまとめて釣り合いの式を積分すると

$I = \int\int\int_V [\delta u(\frac{\partial \sigma_x}{\partial x} + \frac{\partial \tau_{xy}}{\partial y} + X) + \delta v(\frac{\partial\tau_{xy}}{\partial x}+\frac{\partial \sigma_y}{\partial y} + Y)]dxdydz$

$\delta u$, $\delta v$は重みです。z方向の厚みは一定で$t_0$とすると

$I = t_0\int\int_A [\delta u(\frac{\partial \sigma_x}{\partial x} + \frac{\partial \tau_{xy}}{\partial y} + X) + \delta v(\frac{\partial\tau_{xy}}{\partial x}+\frac{\partial \sigma_y}{\partial y} + Y)]dxdy$

ベクトルでまとめましょう

$I = t_0\int\int_A\left[ (\delta u)^{\mathrm T}([L]^{\mathrm T}(\sigma ) + (F )\right)]dxdy$

ここで$( \sigma ) = [D]( \epsilon )$, $( \epsilon ) = [L](u)$より、$( \sigma ) = [D][L](u)$で、積分に代入すると

$I = t_0\int\int_A [(\delta u )^{\mathrm T}([L]^{\mathrm T}[D][L](u) + (F ))]dxdy$

　ここで、有限要素法において重要な変換を入れます。有限要素法は計算する領域を要素に分割します。整った形に分割できればいいのですが、静弾性解析では複雑な形も扱うので、ゆがんだ形の要素になってしまうことがあります。式中の偏微分は方向に依存するので、ゆがんだ要素をそのまま上記の式で計算するととても複雑になってしまいます。そこで、要素から整った形への写像を作り、整った形へ変換してから計算します。これをアイソパラメトリック要素といいます。

今回は領域を四角形の要素に分割し、要素に8個の節点を考えます。節点は四角形の頂点と辺の中点にあるとします。元の要素の節点における変位ベクトルを${d}$とすると、写像によって変換した整った要素の節点変位ベクトルは
$(u) = [N](d)$

となります。$[N]$は変換のための2×8の作用素です。
$[N] = \left[\begin{matrix} N_1&0&N_2&\cdots&N_8&0\
0&N_1&0&\cdots&0&N_8\end{matrix}\right]$
$N_i$は
$N_i(\xi, \eta) = \frac{1}{4}(1+\xi\xi_i)(1+\eta\eta_i)(\xi\xi_i+\eta\eta_i-1)\xi_i^2\eta_i^2+\frac{1}{2}(1-\xi^2)(1+\eta\eta_i)(1-\xi_i^2)+\frac{1}{2}(1-\eta^2)(1+\xi\xi_i)(1-\eta_i^2)$です。
具体的にはグーグル先生で4角形2次要素と調べると詳しく出てくると思います。

上の式を積分に代入して
$I = t_0\int\int_A [(\delta d )^{\mathrm T}([N]^{\mathrm T}[L]^{\mathrm T}[D][L][N](d) + {F})]dxdy$

$[N]^{\mathrm T}[L]^{\mathrm T} = ([L][N])^{\mathrm T}$なので、$[B] = [L][N]$ とおき、

$I = t_0\int\int_A [(\delta d)^{\mathrm T}([B]^{\mathrm T}[D][B](d) + (F))]dxdy$

$\frac{\partial I}{\partial (\delta d )} = 0$となるようにするので($(\delta d )$は重みです)、

$\frac{\partial I}{\partial (\delta d )} = t_0\int\int_A [[B]^{\mathrm T}[D][B](d) + (F)]dxdy = 0$,

$t_0\int\int_A[B]^{\mathrm T}[D][B]dxdy{d} = (F )$

$[K] = t_0\int\int_A[B]^{\mathrm T}[D][B]dxdy$とおくと

$[K](d) = (F)$

となり、単なる連立方程式の形にできます。ちなみに、この$[K]$を剛性マトリックスといいます。

#プログラム
　前置きなげーよ。やっとプログラムを書く段階まで来ました。プログラムの流れとしては
(1)入力データからパラメータを読み込む
(2)剛性マトリックスをつくる
(3)連立方程式を解く
(4)結果を表示する
です。剛性マトリックスをつくるところ以外は特に難しくありません。

##(1)入力データからパラメータを読み込む
　まず要素型、節点型、応力型の３種類の構造体を作ります。有限要素法は要素ごとで計算を行うので、要素を構造体としておくとわかりやすいです。

要素型

type:: element
    integer:: node(8)
    double precision:: ym, po, thick
end type element

要素を構成する節点の番号(node(8))と要素の物理定数(縦弾性係数 ym, ポアソン比 po , 板厚 thick)からなります。

節点型

type:: node
    double precision:: x, y, bcx, bcy
    integer:: xbt, ybt
end type node

節点の座標(x, y)、境界条件の値(bcx, bcy)からなります。xbt, ybtが0ならbcx, bcyは変位、1なら荷重となります。

応力型

type:: stress
    double precision:: xx, yy, xy
end type stress

$\sigma_x$, $\sigma_y$, $\tau_{xy}$をそれぞれxx, yy, xyとしてまとめています。
この他に、変数として要素数(el)、節点数(no)を持っておきます。

次に${d}$としてdvec(:)、$[K]$としてkmat(:, :)を定義します。これらは節点の数によって大きさが変わるのでallocatableとしておきます。
入力データはtxtファイルとして作っておきます。読み込めればなんでもいいですが、ぎっはぶに例(sample.txt)を載せてます。入力するデータは節点の番号と座標、要素を構成する節点と物理定数、境界条件の順番で並んでいます。データを読み込む処理はコード中のread_param()とread_data()で行っています。特に変わったことはしていないので、説明は省略します。

データを読み込むときに構造体と配列を初期化します。
dvecは2no×1次元、kmatは2no×2no次元です。(noは節点数)

##(2)剛性マトリックスをつくる
　コード中ではmake_stiffness()という関数で剛性マトリックスを作っています。剛性マトリックスは

$[K] = t_0\int\int_A[B]^{\mathrm T}[D][B]dxdy$なのでこれを計算します。

まず$[B]$と$[D]$を作ります。コード中ではそれぞれmake_bmat()、make_dmat()です。

$[B] = [L][N]$
$[B] = \left[\begin{matrix} \partial N_1/\partial x&0&\cdots&0\
0&\partial N_1/\partial y&\cdots&\partial N_8/\partial y\
\partial N_1/\partial y&\partial N_1/\partial x&\cdots&\partial N_8/\partial x\end{matrix}\right]$
となるのでこれを作ればいいのですが、

$N_i$の具体的な形は

$$N_i(\xi, \eta) = \frac{1}{4}(1+\xi\xi_i)(1+\eta\eta_i)(\xi\xi_i+\eta\eta_i-1)\xi_i^2\eta_i^2+\frac{1}{2}(1-\xi^2)(1+\eta\eta_i)(1-\xi_i^2)+\frac{1}{2}(1-\eta^2)(1+\xi\xi_i)(1-\eta_i^2)$$
で、$\xi$, $\eta$は写像を通して$x$, $y$と対応しています。コード中ではni()という関数です。

このままだと$x$, $y$で微分できないので、

$\left(\begin{matrix} \partial N_i/ \partial x\
\partial N_i/\partial y\end{matrix}\right) = \left[\begin{matrix}\partial x/\partial \xi&\partial y/\partial \xi\
\partial x/\partial \eta&\partial y/\partial \eta\end{matrix}\right]\left(\begin{matrix} \partial N_i/ \partial \xi\
\partial N_i/\partial \eta\end{matrix}\right)$

で計算します。この作用素はヤコビアン$[J]$ですね。

subroutine make_bmat(nelem, no, nd, xi, eta, bmat, det)
    implicit none
    type(element), intent(in):: nelem
    integer, intent(in):: no
    type(node), intent(in):: nd(no)
    double precision, intent(in):: xi, eta
    double precision, intent(inout):: bmat(3, 16)
    double precision, intent(inout):: det

    integer:: i, j, p
    double precision:: jacobian(2, 2)
    double precision:: dndx, dndy

    !dndx, dndyを計算する
    !jacobianを作る
    jacobian(:, :) = 0.0

    do i=1, 8
      p = nelem%node(i)
      jacobian(1, 1) = jacobian(1, 1) + nd(p)%x * dndxi(i, xi, eta)
      jacobian(1, 2) = jacobian(1, 2) + nd(p)%y * dndxi(i, xi, eta)
      jacobian(2, 1) = jacobian(2, 1) + nd(p)%x * dndet(i, xi, eta)
      jacobian(2, 2) = jacobian(2, 2) + nd(p)%y * dndet(i, xi, eta)
    end do
    !(dndx, dndy)^t = J(dndxi, dndet)^t
    det = jacobian(1, 1)*jacobian(2, 2) - jacobian(1, 2)*jacobian(2, 1)

    bmat(:, :) = 0.0
    !bmatを作る
    do i=1, 8
      dndx = (jacobian(2, 2)*dndxi(i, xi, eta) - jacobian(1, 2)*dndet(i, xi, eta))/det
      dndy = (-jacobian(2, 1)*dndxi(i, xi, eta) + jacobian(1, 1)*dndet(i, xi, eta))/det
      bmat(1, 2*i-1) = dndx
      bmat(2, 2*i) = dndy
      bmat(3, 2*i-1) = dndy
      bmat(3, 2*i) = dndx
    end do

    det = abs(det)
end subroutine make_bmat

$[D]$ は
$[D] = \frac{E}{1-\nu^2}\left[\begin{matrix} 1&\nu&0\
\nu&1&0\
0&0&(1-\nu)/2\end{matrix}\right]$
なのでそのまま作るだけです。

subroutine make_dmat(nelem, dmat)
    implicit none
    type(element), intent(in):: nelem
    double precision, intent(inout):: dmat(3, 3)

    double precision:: f

    f = nelem%ym/(1.0 - nelem%po*nelem%po)
    dmat(1, 1) = f; dmat(1, 2) = nelem%po*f; dmat(1, 3) = 0.0
    dmat(2, 1) = nelem%po*f; dmat(2, 2) = f; dmat(2, 3) = 0.0
    dmat(3, 1) = 0.0; dmat(3, 2) = 0.0; dmat(3, 3) = ((1.0 - nelem%po)/2.0)*f
end subroutine make_dmat

$[B]$, $[D]$ができたら
$[K] = t_0\int\int_A[B]^{\mathrm T}[D][B]dxdy$から$[K]$を作ります。

要素内の積分にはGauss-Legendre積分を使います。Gauss-Legendre積分の４点公式は
$I = \frac{b-a}{2}\sum_{i=1}^4 w_if(r(u_i))$
で、重み$w_i$積分点$u_i$は

$u_1 = -\sqrt\frac{3+2\sqrt{6/5}}{7}, u_2 = -\sqrt\frac{3-2\sqrt{6/5}}{7}, u_3 = +\sqrt\frac{3+2\sqrt{6/5}}{7}, u_4 = +\sqrt\frac{3-2\sqrt{6/5}}{7}$

$w_1 = \frac{18-\sqrt{30}}{36}, w_2 = \frac{18+\sqrt{30}}{36}, w_3 = \frac{18+\sqrt{30}}{36}, w_4 = \frac{18-\sqrt{30}}{36}$です。

do i=1, 4
  xi = gu(i)
  do j=1, 4
     eta = gu(j)
     !bmatを作る
     call make_bmat(elem(ie), no, nd, xi, eta, bmat, det)
     !B^t D Bを計算する
     emat = matmul(transpose(bmat), matmul(dmat, bmat))
     !重みとjacobianのdetをかけて積分
     tmat = tmat + det*emat*gw(i)*gw(j)*elem(ie)%thick
  end do
end do

コード中では要素内の剛性マトリックスをtmat(16, 16)として作り、それを全体の剛性マトリックスkmat(2no, 2no)に足し合わせています。

##(3)連立方程式を解く
　剛性マトリックスができましたので、$[K]{d} = {F}$を計算します。
コード中では連立方程式をLU分解で解いています。solve()というサブルーチンです。
LU分解についてはここでは省略します。

##(4)結果を表示する
　コードでは結果をテキストファイルに出力し、gnuplotでグラフにしています。

#結果

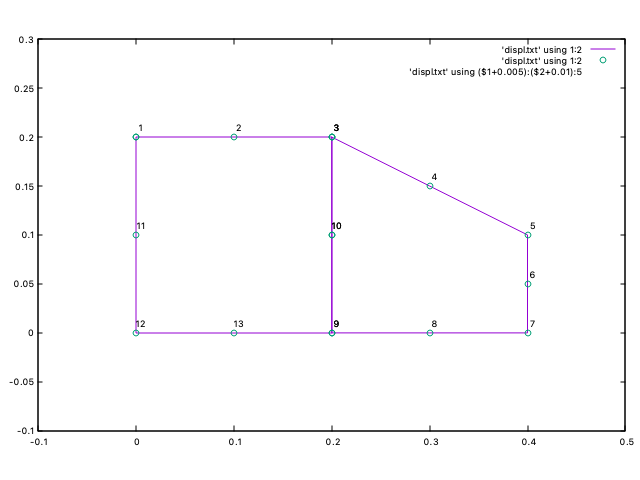
　こんな形の板を解析してみましょう。縦弾性係数は$208\times10^9$ Pa, ポアソン比$0.25$、板厚は左半分が$5\times10^3$ m, 右半分が$3.5\times10^3$ mとします。
境界条件として節点1, 11には$x$方向の変位固定、節点12には$x$, $y$方向の変異固定、節点5に50 N、節点6に75 N、節点7に100 Nの荷重がかかるとします。
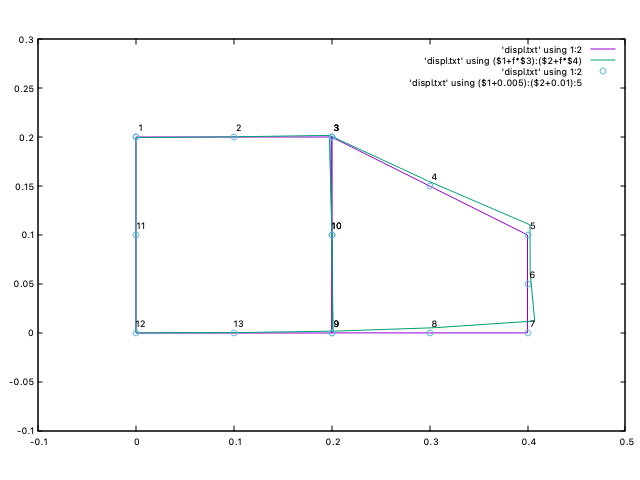
解析すると以下になりました。

荷重がかかったところが引っ張られてゆがんでおり、直感的にも正しそうです。

#まとめ
　有限要素法による静弾性解析をFortranで作ってみました。今回は変位の解析をしましたが、フックの法則を用いれば、応力も計算することができます。コードでは応力計算まで実装してありますので、いずれ説明を加えるかもしれません。

1. https://github.com/PicricAcid/fem_2d
   に置いてあり、それを参照しながら説明していこうと思います。 ↩