この記事は、Elixir Advent Calendar 2023 シリーズ11 の2日目です

昨日は、私で「Elixirで学び直す高校数学①：第3章「方程式で図形を描く」前半～PythonからElixirの世界へようこそ～」でした

piacere です、ご覧いただいてありがとございます

前回からの続きで「Pythonで学び直す高校数学」（以降、本書）をElixir化するシリーズです … なお、本書のコード以外の内容は割愛するため、お手元に書籍をご用意してください

なお、ElixirおよびLivebookのインストールは、前回コラム中で説明しています

あと、このコラムが、面白かったり、役に立ったら、をお願いします

Elixir Advent Calendar 言語カテゴリ1位 & 全カテゴリ2位！

例年を遥かに超える盛り上がりを見せ、堂々のトップ獲得ッ！

https://qiita.com/advent-calendar/2022/elixir
https://qiita.com/advent-calendar/2022/ranking/feedbacks
https://qiita.com/advent-calendar/2022/ranking/feedbacks/categories/programming_languages

2.3 関数とグラフ

本書P96の y = 3x のPythonコードをElixir化するにあたり、ElixirのNumPy相当である「Nx」を使います

最上部の「Notebook dependencies and setup」を下記に変更し、実行することでNxを導入します

Notebook dependencies and setup

Mix.install([
  {:kino_vega_lite, "~> 0.1.10"}, 
  {:nx, "~> 0.6"}, 
])

最初の注意点として、Nxに np.arange 相当は無いため、ほぼ同じことができる np.linspace のNx版である Nx.linspace に入れ替えます

np.arange が、開始／終了／刻み幅のところ、np.linspace および Nx.linspace は、開始／終了／要素数のため、開始／終了／刻み幅から要素数を計算します

y = 3x は、Nxで書くと、下記のようになります

乗算は、Nx.multiply を使います

Nxの行列／テンソルは、そのままではVegaLiteでプロットできないため、Nx.to_list でElixirリストに変換する必要があります

x = Nx.linspace(-1.0, 1.01, n: 201)
y = Nx.multiply(x, 3)
my_data = %{x: Nx.to_list(x), y: Nx.to_list(y)}

実はElixirでも、Python同様、行列／テンソルと数値の計算を計算式で書くこともできますが、defn 内のみ有効（defmodule で囲む必要もあり）なので、計算部分が少ないときは経済的では無いかも知れません（後半の方では、計算多めで有用な例もあります）

x = Nx.linspace(-1.0, 1.01, n: 201)
import Nx.Defn
defmodule Eq23 do
  defn y(x) do
    3 * x
  end
end
my_data = %{x: Nx.to_list(x), y: Nx.to_list(Eq23.y(x))}

グラフにプロットすると、こんな感じになります

ちなみに省略表記を駆使すれば、こんな感じにはできます（が可読性NGですね…）

x = Nx.linspace(-1.0, 1.01, n: 201)
import Nx.Defn
defmodule Eq23, do: defn y(x), do: 3 * x
my_data = %{x: Nx.to_list(x), y: Nx.to_list(Eq23.y(x))}

3️⃣ 直線の方程式

3.1 2点を結ぶ直線

P100の連立方程式は、Elixirでは Nx.LinAlg.solve で解けます

まず、P99の式を下図のように変形します

a + b = 1

5a + b = 3

その上で、Nx.LinAlg.solve の第一引数に左辺の a と b の乗数のみ、第二引数に右辺を行列で渡すと、連立方程式を成立させる a と b を算出します

Nx.LinAlg.solve(Nx.tensor([[1, 1], [5, 1]]), Nx.tensor([1, 3]))

書籍では {a: 1/2, b: 1/2} と分数で表現されていますが、こちらでは 0.5 および近似値と表記は異なるものの同じ結果が出ています

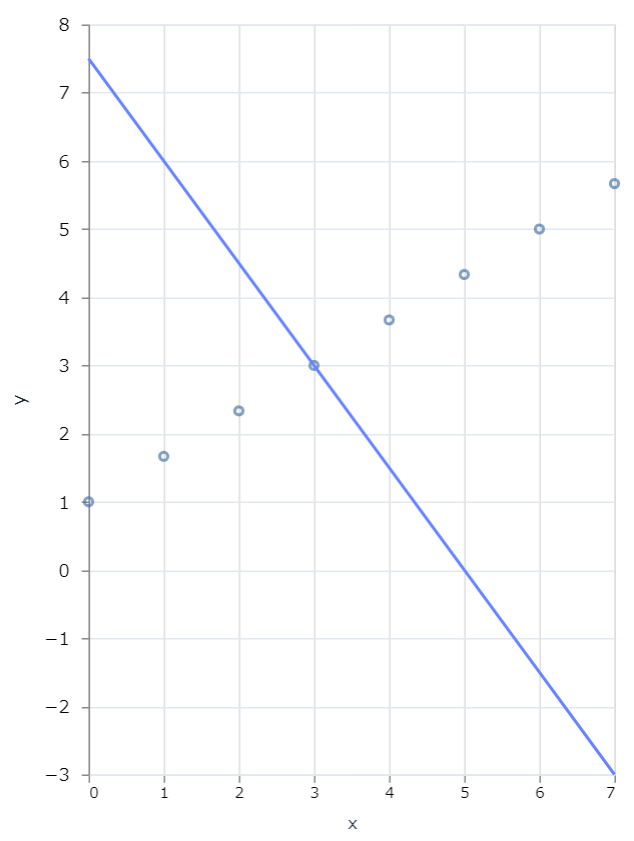
3.2 直交する2本の直線

P102の直交する直線のコードは、Elixirだと下記の通りになります

import Nx.Defn
defmodule Eq32 do
  defn orthogonal(x) do
    %{y: 1/2 * x + 1/2,
      y2: -1 * x + 7}
  end
end

x = Nx.linspace(0, 7, n: 8)
y = Eq32.orthogonal(x)
my_data1 = %{x: Nx.to_list(x), y: Nx.to_list(y.y)}
my_data2 = %{x: Nx.to_list(x), y: Nx.to_list(y.y2)}

「+ Layer」ボタンを追加して、1つ目の「Data」にmy_data1、2つ目の「Data」にmy_data2を設定します

すると、書籍と同じグラフが出ます

3.3 2直線の交点

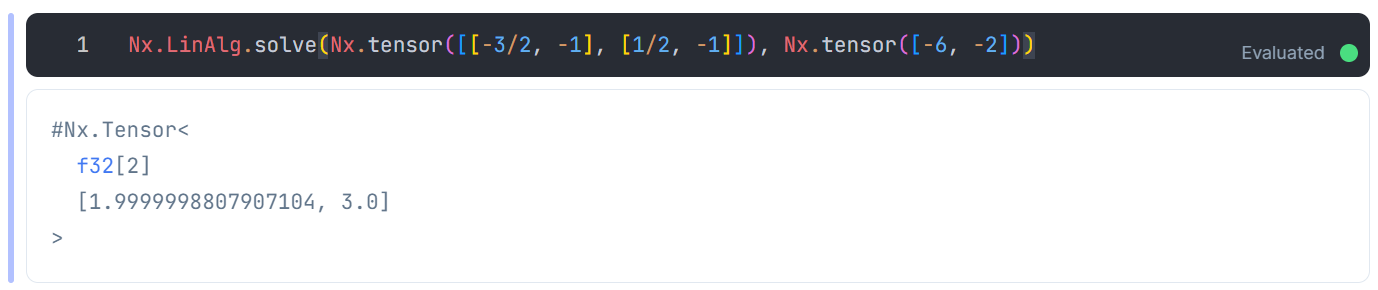
P104の連立方程式も、P103～104の式を下図のように変形して解きます

-3/2x - y = -6

1/2x - y = -2

Nx.LinAlg.solve で x と y を求めます

Nx.LinAlg.solve(Nx.tensor([[-3/2, -1], [1/2, -1]]), Nx.tensor([-6, -2]))

書籍の (2, 3) に近似した値が算出されています

4️⃣ 比例式と三角比

4.1 比例式の性質

（Pythonコードが無いため割愛）

4.2 線分をm:nに内分する点

P109の線分を垂直に二等分する直線のコードは、Elixirだと下記の通りになります

import Nx.Defn
defmodule Eq42 do
  defn bisector(x) do
    # 基となる線分の傾きと切片
    a1 = (5 - 1) / (6 - 0)
    b1 = 1

    # 線分の中点
    cx = (0 + 6) / 2
    cy = (1 + 5) / 2

    # 線分に直交する直線の傾き
    a2 = -1 / a1

    # 線分に直交する直線の切片
    b2 = cy - a2 * cx

    # 直線の式
    %{y1: a1 * x + b1, 
      y2: a2 * x + b2}
  end
end

x = Nx.linspace(0, 7, n: 8)
y = Eq42.bisector(x)
my_data1 = %{x: Nx.to_list(x), y: Nx.to_list(y.y1)}
my_data2 = %{x: Nx.to_list(x), y: Nx.to_list(y.y2)}

結果は本書と同じになります（1つ目の「Chart]にpointを設定しています）

4.3 三角比と円

P114の三角比を使って円を描くコードですが、Nx.sin や Nx.cos に渡すラジアンを度数から計算する np.radians がNxに無いので、度数法からラジアンに変換する無名関数を作って計算します

radians = \frac{degrees}{180} * \pi

radians = fn degrees -> Nx.divide(degrees, 180) |> Nx.multiply(Nx.Constants.pi) end

th = Nx.linspace(0, 360, n: 360)
x = Nx.sin(radians.(th))
y = Nx.cos(radians.(th))
my_data = %{x: Nx.to_list(x), y: Nx.to_list(y)}

結果は、本書と同じです

ちなみに defn を使い、パイプ演算子で変数を無くすと、Elixirらしいコードで書けます

import Nx.Defn
defmodule Eq43 do
  defn radians(degrees) do
    degrees / 180 * Nx.Constants.pi
  end
end

my_data = 
  0..360 |> Enum.to_list |> Nx.tensor
  |> then(& %{
    x: &1 |> Eq43.radians |> Nx.sin |> Nx.to_list, 
    y: &1 |> Eq43.radians |> Nx.cos |> Nx.to_list})

4.4 三角比と角度

P118の三角比から角度を求めるアークタンジェントは、Elixirだと下記の通りです

Nx.atan2(3, 4)

アークタンジェントで求められるラジアンを度数法に変換する np.degrees はNxには無いため、ラジアンから度数法を計算します

degrees = \frac{radians}{\pi} * 180

import Nx.Defn
defmodule Eq44 do
  defn angle_from_two() do
    Nx.atan2(3, 4) / Nx.Constants.pi * 180
  end
end

Eq44.angle_from_two

結果は、本書と同じです

最後に

今回は、方程式の攻略にPythonのNumPy相当である「Nx」が登場しました

Nxのさまざまな行列／テンソル操作後とグラフ化がLivebook上で直感的に行える様が見えたかと思います

また、defn を使えば、数式がそのままプログラミングできることも示しました

連立方程式の解決も、Nx.LinAlg.solve で簡単に実現できました

円描画や角度計算などもNxを使うことで片付きました

Nxはこれらのような数学処理を行う上で、とても便利です

p.s.サブタイトルは「ノーガード戦法」のもじりでした

明日は、@t-yamanashi さんで「[改善版]言語聴覚リハビリ答えあわせプログラム　～数字、仮名ソート～」です

p.s.このコラムが、面白かったり、役に立ったら…

にて、どうぞ応援よろしくお願いします

Elixirで学び直す高校数学②：第3章「方程式で図形を描く」中盤 ～ノーコード戦法でグラフ描けるElixir～