PRMLの第8章「グラフィカルモデル」やGoodfellowの第16章「深層学習のための構造化確率モデル」を読んで、グラフィカルモデルを勉強しました。PRMLにもある応用例「画像のノイズ除去」をpythonで実装したので、この投稿では、無向グラフやそのポテンシャル関数についての知識を前提に、解説を行います。
理論
任意の1チャンネル(=グレースケール)入力画像を受け取り、二値化します。二値化とは適当な閾値より大きい画素値を255,閾値以下の画素値を0にすることです。その後、この画像の各ピクセルに、画素値が0なら-1,255なら+1を割り当てます。この配列をAとします。この配列に適当なノイズを与えます。「ノイズを与える」とは、Aの各ピクセルに割り当てられた値$\pm1$の符号を一定の確率で反転させることを指します。Aにノイズを与えたあとの配列をyとします。以下のアルゴリズムの目的は、yからAを推測することです。この作業を「画像のノイズ除去」と呼ぶことにします。
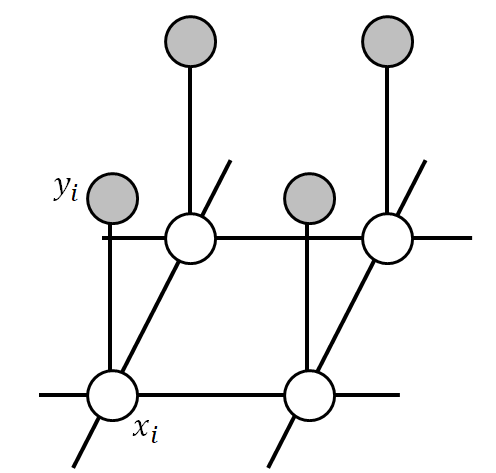
推測されるAの各要素を$\{x\}$で表すことにします。ノイズレベルが低ければ$x_i$と$y_i$との間には強い相関がありそうです。ただし、$i$はピクセルの通し番号です。また、画像中の隣接するピクセルは同じ画素値を持つ確率が高いという仮定から、画像中の隣接ピクセル$x_i$と$x_j$の間にも強い相関がありそうです。これらの背景となる知識は、図の無向グラフで表現されます。
ノード同士を結ぶエッジは互いに相関があることを意味しています。この無向グラフには$\{x_i,y_i\}$の形のクリークと、$\{x_i,x_j\}$の形のクリークが存在します(ただし、$i$と$j$は隣接するピクセル番号で$i$を固定すると$j$は4通り存在します)。前者のクリークには正の定数$\eta$を用いて、$-\eta x_i y_i$というエネルギー関数を採用します。$x_i$と$y_i$の符号が等しい時にエネルギーが低く、実現確率が高いことが分かります。後者のクリークには正の定数$\beta$を用いて$-\beta x_i x_j$というエネルギー関数を用います。これも隣接するピクセル間の画素値($+1$または$-1$)が同じであればエネルギーが高く、実現確率が高いことを意味しています。
また、各ピクセルの値が特定の符号を持ちやすくなるようなバイアスをかける項として、$hx_i$という項を追加します。ここで$h$は$-1$から$+1$の間の実数です。以上を整理すると、無向モデルの同時分布$p({\bf x},{\bf y})$は全エネルギー関数
$$
E({\bf x,y}) = h \sum_i x_i - \beta\sum_{\{i,j\}}x_ix_j-\eta\sum_ix_iy_i
$$
を用いて
$$
p({\bf x},{\bf y}) = \frac{1}{Z}{\rm exp}\{-E({\bf x,y})\}
$$
とかけます。ここで$Z$は分配関数と呼ばれる規格化定数です。この同時分布$p({\bf x},{\bf y})$を最大にするために、エネルギー関数$E({\bf x,y})$が最小になるような集合$\{x\}$を求めます。なお$x_i$をスピン変数、$y_i$を磁場とみなせば、この同時分布$p({\bf x},{\bf y})$は統計力学における2次元イジング模型のカノニカル分布と一致することがわかります。ただし、通常のイジング模型とは異なり磁場の向きは場所によって異なります。この模型はtwo dimensional random field ising modelなどと呼ばれます。
実装
結果だけを見たい人はこの章を飛ばしてください。
まずは入力画像にノイズを与える関数を用意します。入力画像noised_imageにノイズを与えて、noised_imageとして出力します。degree_of_noiseは0から1の値をとり、ノイズの激しさを表します。
def noise(noised_image,degree_of_noise):
noised_width = noised_image.shape[0]
noised_height = noised_image.shape[1]
for i in range(0,noised_width):
for j in range(0,noised_height):
rd = rand()
if rd > (1-degree_of_noise):
noised_image[i][j] = (-1)*noised_image[i][j]
return noised_image
次に全エネルギー関数を計算する関数を用意します。入力配列parametersには順に$h,\beta,\eta$が格納されています。sum1は$h \sum_i x_i$を表し、sum2は$\beta\sum_{\{i,j\}}x_ix_j$をあらわし、sum3は$\eta\sum_ix_iy_i$を表しています。配列の範囲外を参照しないように、forループは(2,width-2),(2,height-2)を回します。
def energy(x,noised_image,parameters):
width = x.shape[0]
height = x.shape[1]
#第一項
sum1 = np.sum(x)
#第二項
sum2 = 0
for i in range(2,width-2):
for j in range(2,height-2):
sum2 = sum2 + x[i][j]*(x[i][j+1] + x[i][j-1] + x[i+1][j] + x[i-1][j])
#第三項
sum3 = np.sum(x*noised_image)
return parameters[0]*sum1 - parameters[1]*sum2 - parameters[2]*sum3
次に集合$\{x\}$を全エネルギー関数$E({\bf x,y})$が最小にするように更新するoptimizerを定義します。optimizer_randomでは集合$\{x\}$からランダムに$x_j$を1つ取り出し、$x_j$が+1の時と、-1のときでどちらが全エネルギー関数$E({\bf x,y})$が小さくなるかを調べ、$x_j$を全エネルギー関数を小さくする$x_j$に更新します。入力変数trialはこの試行を繰り返す回数です。show_energyをTrueにすると定期的に全エネルギー関数$E({\bf x,y})$の値をコンソール上に出力し、その値を配列engに保存します。また、image_save=Trueにすると定期的に復元途中の画像を保存します。この関数は、2次元配列$x$と各試行における全エネルギー関数の値を格納した1次元配列eng_arrayと各試行における正解率を格納した1次元配列acc_arrayを返します。
def optimizer_random(original_image,x,noised_image,parameters,trial=1500000,show_detail=True,image_save=True):
width = x.shape[0]
height = x.shape[1]
#エネルギーの値を格納する。
eng_array = [] #エネルギーの値を格納する。
acc_array = [] #正解率を格納する。
times_array = [] #試行回数を格納する。
start = time.time()
for cnt in range(0,trial):
p = random.randint(1, width-2)
q = random.randint(1, height-2)
x[p][q] = +1
E1 = h*x[p][q]-beta*x[p][q]*(x[p][q+1] + x[p][q-1] + x[p+1][q] + x[p-1][q])-eta*x[p][q]*noised_image[p][q]
x[p][q] = -1
E2 = h*x[p][q]-beta*x[p][q]*(x[p][q+1] + x[p][q-1] + x[p+1][q] + x[p-1][q])-eta*x[p][q]*noised_image[p][q]
if E2 < E1:
x[p][q] = -1
else:
x[p][q] = +1
if show_detail == True and cnt % 5000 == 0:
eng = energy(x,noised_image,parameters)
acc = accuracy(original_image,x)
acc_array.append(acc)
eng_array.append(eng)
times_array.append(cnt)
print("Energy:"+str(round(eng,2)),"Accuracy:"+str(round(acc,2)),"Progress:"+str(round(cnt/trial*100,2)),"%","Time:",round(time.time() - start,2),"[sec]")
if image_save == True and cnt % 50000==0:
cv2.imwrite("save/random"+str(cnt)+".jpeg",x*255) #どういうわけか255倍するとうまく保存できる。
return x,eng_array,acc_array,times_array
optimizer_scanでは、同様に集合$\{x\}$の各要素を全エネルギー関数$E({\bf x,y})$が最小になるように更新しますが、更新するか否かを判定する$x_j$をランダムに選ぶのではなく、左上から1ピクセルずつ順に選択されていきます(ラスタスキャン)。全$x$について、optimizer_randomと同じ手続きをtrial回繰り返します。
実際には、optimizer_randomかoptimizer_scanのどちらか一方を選択して使用してください。main関数ではデフォルトで、optimizer_scanになっていますが、必要に応じてoptimizer_randomに書き換えてください。
def optimizer_scan(original_image,x,noised_image,parameters,trial=5,show_detail=True,image_save=True):
width = x.shape[0]
height = x.shape[1]
cnt = 0
eng_array = [] #エネルギーの値を格納する。
acc_array = [] #正解率を格納する。
times_array = [] #試行回数を格納する。
start = time.time()
for l in range(1,trial):
for p in range(1,width-1):
for q in range(1,height-1):
x[p][q] = +1
E1 = h*x[p][q]-beta*x[p][q]*(x[p][q+1] + x[p][q-1] + x[p+1][q] + x[p-1][q])-eta*x[p][q]*noised_image[p][q]
x[p][q] = -1
E2 = h*x[p][q]-beta*x[p][q]*(x[p][q+1] + x[p][q-1] + x[p+1][q] + x[p-1][q])-eta*x[p][q]*noised_image[p][q]
if E2 < E1:
x[p][q] = -1
else:
x[p][q] = +1
cnt = cnt + 1
if show_detail == True and cnt % 5000 ==0:
eng = energy(x,noised_image,parameters)
acc = accuracy(original_image,x)
eng_array.append(eng)
acc_array.append(acc)
times_array.append(cnt)
print("Energy:"+str(round(eng,2)),"Accuracy:"+str(round(acc,2)),"Progress:"+str(round(cnt/(trial*(width-2)*(height-2))*100,2)),"%","Time:",round(time.time() - start,2),"[sec]")
if image_save == True:
cv2.imwrite("save/scan"+str(l)+".jpeg",x*255) #どういうわけか255倍するとうまく保存できる。
return x,eng_array,acc_array,times_array
正解率Accuracyを計算する関数を用意します。2次元配列np.abs(original_image-modified_image)は、original_imageの$(i,j)$成分の値と2次元配列modified_imageの$(i,j)$成分の値が同じであれば$0$を、異なれば$2$を$(i,j)$要素に格納します。この2次元配列の各要素の和np.abs(original_image-modified_image).sum()の大きさがoriginal_imageとmodified_imageがどれほど異なるかを表しています。これを規格化し、1から引いた値をAccuracyとして定義します。この定義から、input画像にノイズを与えた画像noised_imageのAccuracyは(1-degree_of_noise)になることがわかります。
def accuracy(original_image,modified_image):
miss = (np.abs(original_image-modified_image)).sum()/(2.0*modified_image.shape[0]*modified_image.shape[1])
return 1.0-miss
グラフをプロットして保存する関数を用意します。
def plot_graph(times_array,eng_array,acc_array):
#エネルギー関数の時間変化の様子をプロット
plt.plot(times_array,eng_array)
plt.title("h="+str(h)+" beta="+str(beta)+" eta="+str(eta))
plt.xlim([0,1400000])
plt.xlabel("Trial",fontsize=14)
plt.ylabel("Energy",fontsize=14)
plt.gca().ticklabel_format(style="sci", scilimits=(0,0), axis="x")
plt.gca().ticklabel_format(style="sci", scilimits=(0,0), axis="y")
plt.tight_layout() #labelがはみ出ないように自動調整
plt.savefig('save/energy.png')
plt.show()
#正解率の時間変化の様子をプロット
plt.plot(times_array,acc_array,color='red')
plt.title("h="+str(h)+" beta="+str(beta)+" eta="+str(eta))
plt.xlim([0,1400000])
plt.ylim([0.8,1.0])
plt.xlabel("Trial",fontsize=14)
plt.ylabel("Accuracy",fontsize=14)
plt.gca().ticklabel_format(style="sci", scilimits=(0,0), axis="x")
plt.tight_layout() #labelがはみ出ないように自動調整
plt.savefig('save/accuracy.png')
plt.show()
main関数を用意します。h,beta,etaはそれぞれ$h,\beta,\eta$を表します。
if __name__ == "__main__":
show_detail = True #エネルギー関数や経過時間,正解率を表示するならTrue,しないならFalse
image_save = True #途中経過を画像として保存するならTrue,しないならFalse
#読み込む画像のファイル名
input_image = "truth.png"
#相互作用係数の大きさ
h = 0.0 #-1から+1の実数
beta = 1.0 #正の実数
eta = 2.1 #正の実数
parameters = [h,beta,eta]
#degree_of_noiseは与えるノイズの大きさ。0から1の間をとる。
degree_of_noise = 0.10
if degree_of_noise > 1 or degree_of_noise < 0:
print("ノイズの大きさを決めるdegree_of_noiseの値が異常です。")
sys.exit()
#画像等を保存するディレクトリをつくる
if not os.path.exists("save"):
os.mkdir("save")
#グレースケールで画像を読み込む
original_image = cv2.imread(input_image,cv2.IMREAD_GRAYSCALE)
original_image = cv2.resize(original_image,(500,500))
original_image = original_image/255
#画像を2値化した後に各ピクセル値が0なら-1,1なら1を格納する。
ret,original_image = cv2.threshold(original_image,0.5,1,cv2.THRESH_BINARY)
original_image = np.where(original_image == 1, +1, original_image)
original_image = np.where(original_image == 0, -1, original_image)
#noised_imageにはoriginal画像にノイズを与えた画像を保存する。
noised_image = copy.deepcopy(original_image)
noised_image = noise(noised_image,degree_of_noise)
#modified_imageにはノイズを取り除いた画像を保存する。
modified_image = copy.deepcopy(noised_image)
modified_image,eng_array,acc_array,times_array = optimizer_scan(original_image,modified_image,noised_image,parameters,show_detail=show_detail,image_save=image_save)
#正解率を求める。
acc = accuracy(original_image,modified_image)
print("最終正解率:",acc)
#グラフを表示
if show_detail:
plot_graph(times_array,eng_array,acc_array)
#最終結果を表示
cv2.imshow("Modified image",modified_image)
cv2.waitKey(0)
#最終結果を保存
cv2.imwrite("save/modified_image.jpeg",modified_image*255)
cv2.imwrite("save/noised_image.jpeg",noised_image*255)
なお、パラメータ$\eta$と$\beta$の調整をする際は次のコードをmain関数内の適当な場所に書いて実行します。
#パラメータ空間をM×Nに分割する。
M = 300
N = 300
eta_array = np.linspace(0.0, 3, M)
beta_array = np.linspace(0.0, 3, N)
acc_matrix = np.zeros(M*N) #各パラメータでの精度を保存する。
cnt = 0 #内側のforループの回った回数を記録
for i in range(0,M): #eta
eta = eta_array[i]
for j in range(0,N): #beta
beta = beta_array[j]
parameters = [h,beta,eta]
modified_image = copy.deepcopy(noised_image)
modified_image,eng_array,acc_array,times_array = optimizer_scan(original_image,modified_image,noised_image,parameters,show_detail=show_detail,image_save=image_save)
acc = accuracy(original_image,modified_image) #精度を計算し、各パラメータでの精度を保存する。
acc_matrix[cnt] = acc
cnt = cnt + 1
print(round(cnt*100/(M*N),2),"%終了",acc)
X, Y = np.meshgrid(beta_array, eta_array) #ひっくり返ってるように見えるが正しい
acc_matrix = np.reshape(acc_matrix, (M, N)) #カラープロット用に変形
plt.pcolor(X, Y, acc_matrix) #カラープロット
cbar = plt.colorbar() # カラーバーの表示
cbar.set_label('Accuracy', fontsize=16)
plt.title("degree of noise="+str(degree_of_noise))
plt.xlabel("β",fontsize=16)
plt.ylabel("η",fontsize=16)
plt.clim(0.5,1.0) #カラーバーの範囲
plt.tight_layout() #labelがはみ出ないように自動調整
plt.savefig("save/parameters"+str(degree_of_noise)+".png")
plt.show()
実験
拾ってきたチェッカー画像を傾けた画像をinput_imageとして入力します。チェッカー画像の白黒比は同じなので、$h=0$とします。PRMLに倣い$\beta=1.0,\eta=2.1$とします。 degree_of_noise = 0.10としました。optimizer_scanで最適化した場合もoptimizer_randomで最適化した場合も十分な試行回数の末にはノイズがややとれていることが確認できます。
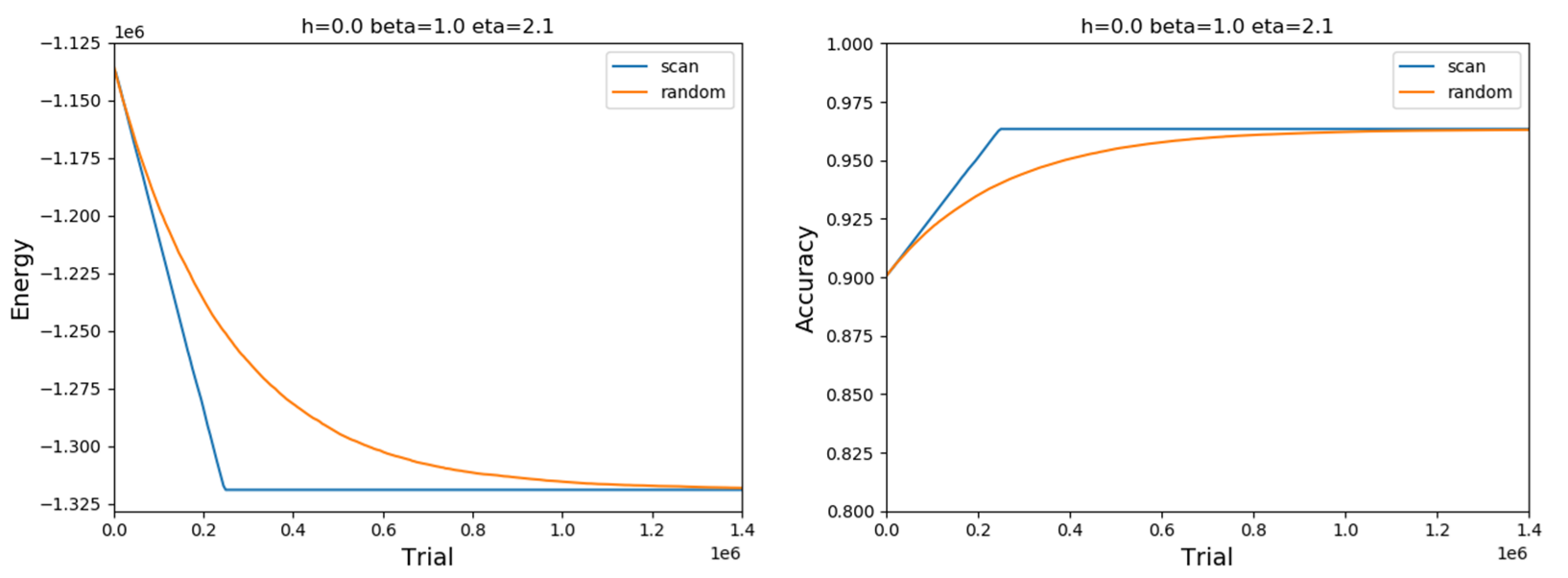
optimizer_scanおよびoptimizer_randomで最適化した場合の全エネルギー関数$E({\bf x,y})$と正解率の時間変化をプロットしてみました。
明らかにoptimizer_scanで最適化した方が早くノイズ除去が完了することが分かります。ここでAccuracyは96%程度ですが、パラメータチューニングによってより高いAccuracyを実現できないか実験してみます。
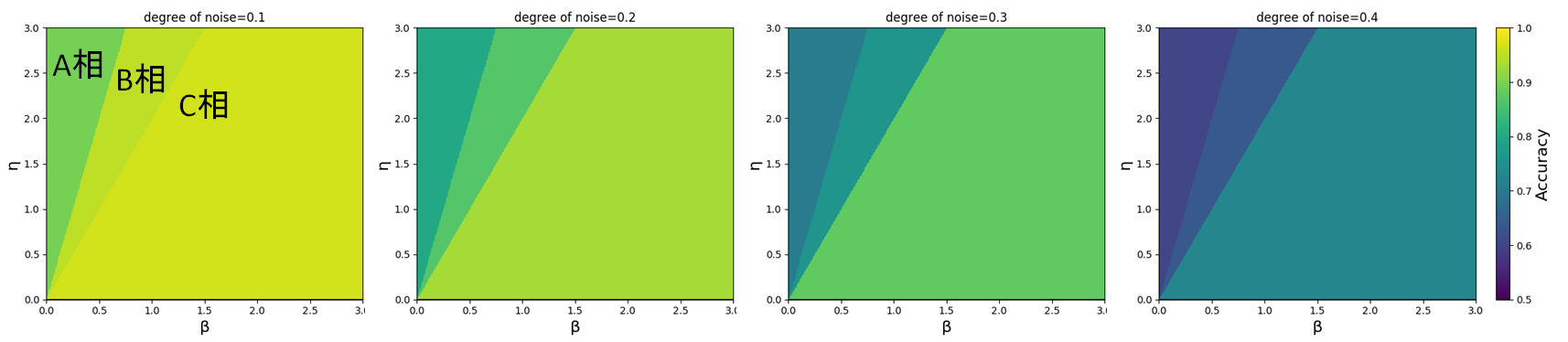
各$\eta,\beta$でのAccuracyをカラープロットした様子です。明るい色はよりAccuracyが高いことを意味しています。
$\beta$または$\eta$を固定してもう一方のパラメータを連続的に変化させると、Accuracyは不連続に変化しています。図からもわかるように、$\beta$と$\eta$の比がAccuracyを決定します。これは
\begin{align}
\{x\} &= {\rm argmin}_{\{x\}} \left(- \beta\sum_{\{i,j\}} x_ix_j-\eta\sum_ix_iy_i\right) \\
&= {\rm argmin}_{\{x\}} \left(- \frac{\beta}{\eta}\sum_{\{i,j\}} x_ix_j-\sum_ix_iy_i\right)
\end{align}
であることから理解できます。また、ノイズの激しさdegree of noiseを大きくするにつれて、プロットされる色が濃くなっていく(=Accuracyが低い)ことからノイズ除去が難しくなっていく様子も見て取れます。一方で図から見て取れる非自明な事実として、
- degree of noiseの値に関わらず$\beta,\eta$の比によって3つの相が出現する($\beta$が小さい領域から順にA相、B相、C相と定義します)。
- 相を分かつ直線の傾きはdegree of noiseに影響を受けていないように見える。
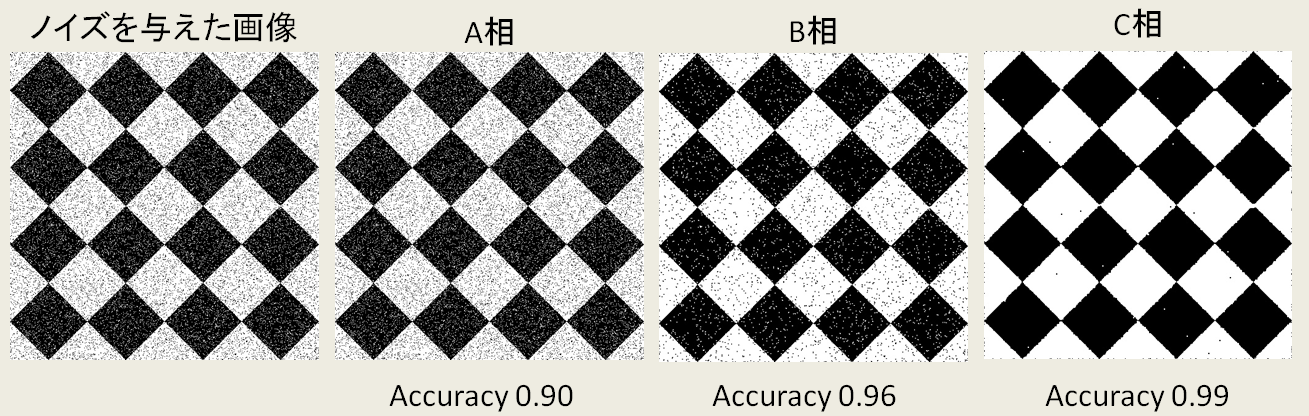
があります。初めに実験した$\beta=1.0,\eta=2.1$は3つの相のうちAccuracyが2番目に大きくなるB相でした。$\eta=1$として$\beta$を連続的に変化させ、A相,B相,C相で復元画像$\{x\}$がどのように変化するかを表した様子が以下です。各層では画像$\{x\}$は全く同じものになります。なお、degree_of_noise = 0.10としました。明らかにC相のAccuracyが最も高いことが分かります。PRMLでは96%のAccuracyを実現した例が載っていますが、実はパラメータを適切に選ぶことで99%のAccuracyを実現できるという訳です。
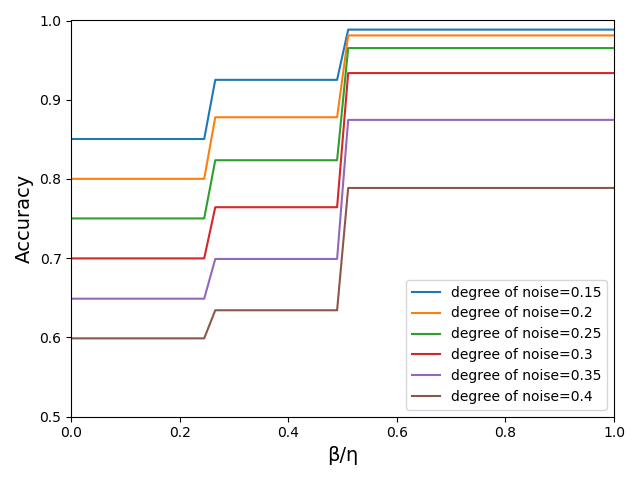
次に、異なるdegree of noiseでも、A相→B相→C相という変化が起こる$\beta,\eta$の比が同じであることを確認します。下の図から$\frac{\beta}{\eta}=0.25,0.5$で相が変化することが分かります。A相のAccuracyは(1-degree_of_noise)になっていることがわかります。つまりA相のAccuracyはノイズを与えた画像と全く同じで、ノイズが全く除去されていないことが分かります。
ところで、「パラメータ空間上にAccuracyをプロットすると、A相,B相,C相が現れ、各相を分かつ直線の式が$\beta=0.25\eta$,$\beta=0.5\eta$である」というのはチェッカーボード画像に固有の事実なのか、あるいは画像によらず普遍的な定理なのかが気になるところです。
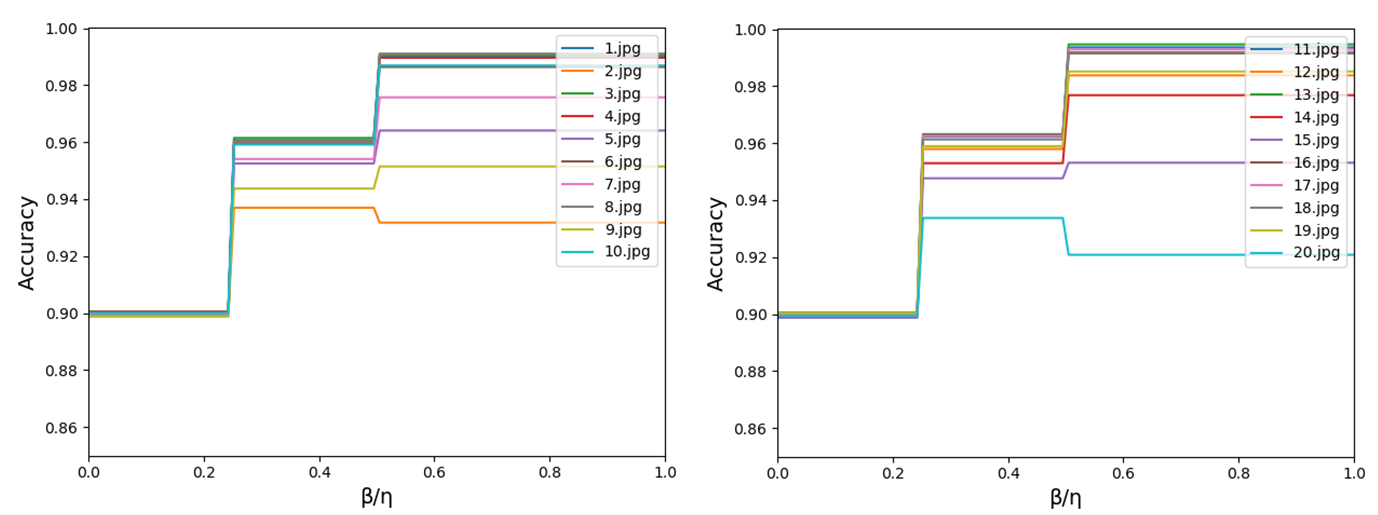
そこで、input画像を様々に変え、hを0に固定して、同様に$\beta$と$\eta$の比によってAccuracyがどのように変化するかを観察します。入力画像1.jpgから20.jpgの一覧と結果のグラフが以下です。degree of noiseは10として、入力画像のサイズはいずれも500×500としました。
グラフから次のことが分かります。
- 画像によらず、$\beta$と$\eta$の比によってA相,B相,C相が現れる。
- 各相の境目となる$\beta$と$\eta$の比も画像に依存しない。
ただし、結果のグラフをよく見てみると、2.jpgや20.jpgでは、B相とC相のAccuracyの大小が逆転しています。つまり、必ずしも$\beta>0.5\eta$が最適なパラメータであるとは限らない、ということです。
以上から、このアルゴリズムを用いてノイズ除去を行う場合、パラメータは、$\beta>0.5\eta$と$0.25\eta<\beta<0.5\eta$の二通りを試して、精度の良い方を採用すればよいということが言えそうです。
物理の問題に焼き直して考察する
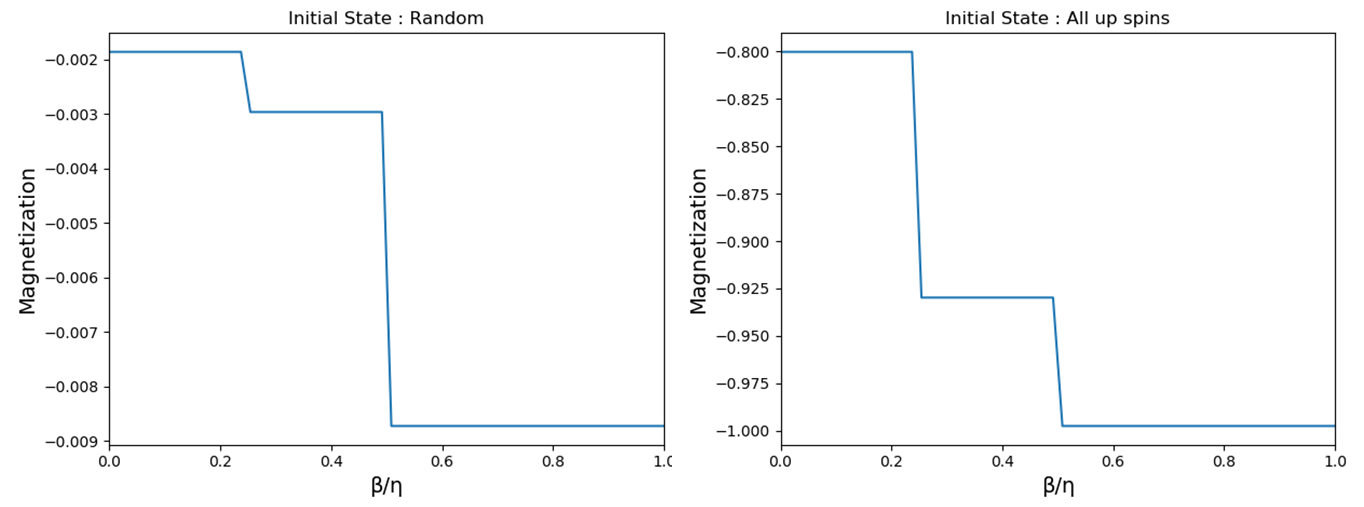
以上の議論を物理の問題に焼き直してみます。ランダムな初期状態(下図:上)と完全にスピンがアップにそろっている初期状態(下図:下)に、各サイトにランダムな磁場を与え、各磁場の大きさでスピン配位がどうなっているかを見てみました。ここでいう、ランダムな磁場とは、各サイトにおいて確率1/2で上向き、確率1/2で下向きの大きさ$\eta$の磁場のことです。磁場の効果が大きいA相ではランダム磁場に近い結果になる一方で磁場が弱いC相では、隣接するサイト間の結びつきが強いために白と黒がA相,B相に比べて固まっている印象を受けます。
上の図では、各サイトにおいて確率1/2で上向き、確率1/2で下向きの大きさ$\eta$の磁場を各初期状態に与えましたが、この確率は、1-degree_of_noiseに対応し、初期状態はinput画像に対応します。そこで今度は、各サイトにおいて確率9/10で上向き、確率1/10で下向きの大きさ$\eta$の磁場を各初期状態に与えました。これはdegree_of_imageを0.1にすることに対応しています。
各サイトでのスピン和をとった磁化をプロットすると、明らかに磁化が不連続に変化しています。つまり、Accuracyが不連続に変化する$\frac{\beta}{\eta}=0.25,0.5$というパラメータは、two dimensional random field ising modelにおける磁化が不連続に変化する点に対応していた訳です。
この事実は既知なのでしょうか。文献をご存知の方がいれば教えてほしいです。