面積比から円周率を求める。pythonで実装。

半径１の円に外接する正方形の一辺の長さは2です。
半径１の円の面積は$ \pi $,一辺の長さが2の正方形の面積は4なので、この正方形から内接する円を取り除いた図形の面積は$4-\pi$です。

つまり、この正方形内にランダムに点を十分な数、打っていったときに、円の外にある点と円の内側にある点の数の比は$4-\pi:\pi$であるはずです。円の外側の点の数を$\alpha$,内側の点の数を$\beta$としたとき、円周率$ \pi $は、

\pi = \frac{4\beta}{\alpha+\beta}

とかけます。この事実から、円周率$ \pi $を求めてみました。

pi.py

import random
import math
import numpy as np
import matplotlib.pyplot as plt

if __name__ == "__main__":

	number_of_trial = 1000
	history = np.zeros(number_of_trial)
	difference = np.zeros(number_of_trial)

	alpha = 0.0
	beta = 0.0

	for cnt in range(0,number_of_trial):

		xp = random.uniform(-1.0,1.0)
		yp = random.uniform(-1.0,1.0)

		if xp*xp+yp*yp > 1.0:
			alpha = alpha + 1.0

		else:
			beta = beta + 1.0

		history[cnt] = 4.0/(beta+alpha)*beta
		difference[cnt] = abs(math.pi-history[cnt])

	plt.hlines([math.pi], 0, number_of_trial, "red", linestyles='dashed')
	plt.xlim([0,number_of_trial])
	plt.plot(history)
	plt.show()

	plt.plot(difference,color='#4daf4a')
	plt.xlim([0,number_of_trial])
	plt.ylim([0,0.5])
	plt.show()

横軸がプロットした点の数。縦軸が計算によって求められた円周率$ \pi $。赤い線が本物の円周率。

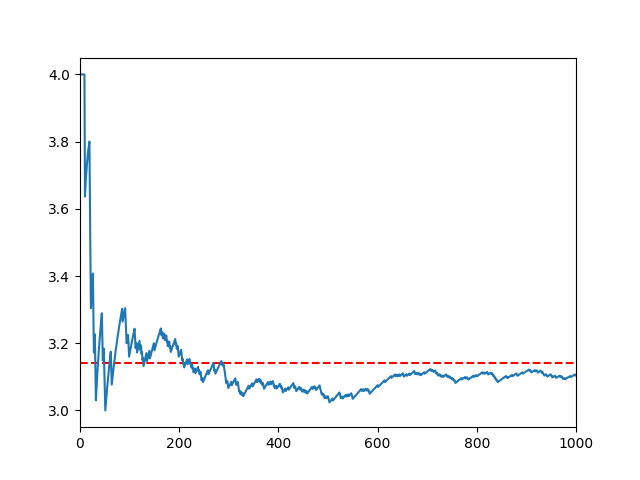
本物の円周率から計算によって求められた円周率の差の絶対値をプロットしたもの。

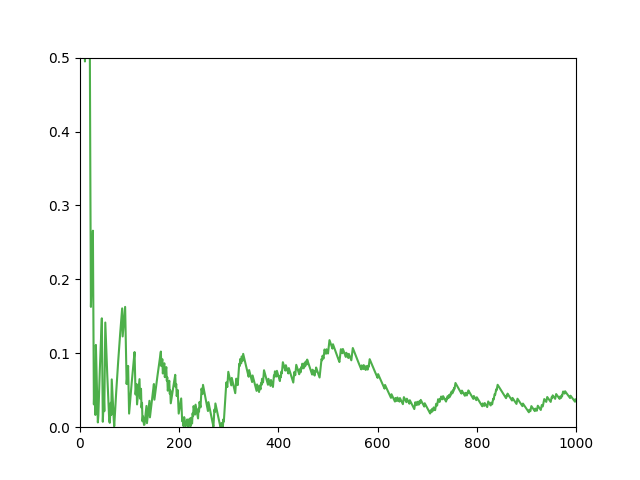
う～ん、1000回程度じゃあんまりよい値はでないですね。