フラクタルは数学やプログラミングの教材としてとても良いですね。練習がてらにスクラッチしたフラクタル図形を紹介します。
理論の解説はしません。
マンデルブロ集合
全体のコードはこちら。
フラクタルと言えば、マンデルブロ集合ですよね。
定義
$z_0=0, z_{n+1} = z_n^2 + C$で定義される複素数列$\{z_n \}$が$n \to \infty $ で発散しない複素平面上の点$C$の集合をマンデルブロ集合と呼ぶ。
ここで複素数列$\{z_n \}$が$n \to \infty $で発散しない、というのは、$|z_n|$が$n \to \infty $で発散しないことを言います。また、$|z_k| > 2$ を満たす $z_k$が存在する場合は$\{z_n \}$がいずれ発散することが知られています。この命題の説明はこちらにあります。
そこで、各$C$に対して$\{z_n \}$を100項目まで求めて、絶対値が2を超えるものがあるか否かで収束判定を行います。マンデルブロ集合には様々な彩色方法がありますが、今回は、収束判定に要したiterの回数に伴ってカラーリングをすることにします。
solutions = np.array([2.7693, 0.11535-0.58974J, 0.11535+0.58974J])
def f(z, C):
return z*z + C
def convergence_judgment(C):
z = inital_z # 0.0
i = 0
while i < 100:
z = f(z, C)
if abs(z) > 2:
return i #2を超える最小の|z_n|に対応するnをかえす。
i += 1
return i #発散しない場合は100をかえす。
main関数では、中心座標center_positionを中心とした一片の長さがepsilonの長方形をN×Nのgridに小分けして、各gridにおいて収束判定を行う旨を書きます。
N = 1000
inital_z = 0
epsilon = 1 #<2
center_position = [0, 0]
def main():
grid = np.empty((N, N), dtype=np.uint8)
points_x = np.linspace(center_position[0]-epsilon, center_position[0]+epsilon, N)
points_y = np.linspace(center_position[1]-epsilon, center_position[1]+epsilon, N)
for n, ReC in tqdm(enumerate(points_x)):
for m, ImC in enumerate(points_y):
C = ReC + ImC*1J
grid[m, n] = convergence_judgment(C)
show(grid)
このコードでは計算時間はN=1000でおよそ100秒でした。画像クリックで拡大。
 |
 |
 |
|---|---|---|
| (0,0) | (-0.53 -0.613) | (-0.76,0.067) |
なお、マンデルブロ集合の定義から外れてしまいますが、初項$z_0$を変えてみると、これまた特徴的な様子が見えてきて楽しいですよ!それと、z^2 + C の指数2を色々かえてみて任意のnについて z^n + C のつくる模様をみてみると楽しいですよ!
ニュートンフラクタル
全体のコードはこちら。
例えば複素数$z$に関する3次方程式
$$
z^3-3z^2+z-1=0\tag{1}
$$
は3つの解をもつ。怠慢なのでMathicsなどで次のように入力すれば、解が求まりますね。
複素平面上の任意の点を始点$z_0$として、ニュートン法
$$
z_{n+1} = z_{n} - \frac{f(z_n)}{f'(z_n)}
$$
で$z$を更新していって方程式(1)の解を見つけることを考えます。もちろん、方程式(1)の左辺は$z$に関して単調ではないので、ニュートン法によって解が求まるかは分かりません。適当に選んだ$z_0$に対して、ニュートン法の結果
- 解1にたどり着く
- 解2にたどり着く
- 解3にたどり着く
- どこにもたどり着かない(ニュートン法によって収束しない)
のいずれかの結果が得られます。ニュートン法の各始点$z_0$に対して上記1~4のどの結果が得られるかによって複素平面上の点$z_0$を色付けします。
def f(z):
return z**3-3*z**2+z-1
def diff_f(z):
return 3*z**2-6*z+1
def find_nearest_solution_idx_and_residual(z):
nearest_solution_idx = abs(z-solutions).argmin()
residual = abs(z - solutions[nearest_solution_idx])
return nearest_solution_idx, residual
def solve_f(inital_z):
z = inital_z
for n in range(max_step):
z = z - f(z) / diff_f(z)
nearest_solution_idx, residual = find_nearest_solution_idx_and_residual(z)
if residual < residual_criteria: #convergence judgment
return nearest_solution_idx + 2*n/max_step
return len(solutions)
すると以下のようなフラクタルが現れます。計算時間はN=2500で24分でした。
 |
 |
 |
|---|
方程式をいろいろ変えてみて遊んでみると楽しいですよ!
[1] 稲生啓行 複素力学系と計算可能性
シェルピンスキーのギャスケット
全体のコードはこちら
シェルピンスキーのガスケットのガスケットは次のアルゴリズムで生成されます。
- 正三角形(a1, a2, a3)の座標を適当に決める。
- 正三角形(a1, a2, a3)の各辺の中点を結ぶ。
- 2.の手続きによって出現した4つの三角形のうち、中央の三角形を除く3つの三角形について2を行う。
以下のソースコードでは、便利なので座標に複素数を用いていますが、これは本質ではありません。triangleは3つの要素を持つリストで、各要素が三角形の頂点の複素座標に対応しています。
# ひとつの三角形から三つの三角形を生成する。
def make_3triangles_from_triangle(triangle):
p0 = triangle[0]
p1 = triangle[1]
p2 = triangle[2]
new_p2 = (m*p0 + n*p1) / (m+n)
new_p0 = (m*p1 + n*p2) / (m+n)
new_p1 = (m*p2 + n*p0) / (m+n)
triangle0 = [p0, new_p1, new_p2]
triangle1 = [new_p1, p2, new_p0]
triangle2 = [new_p2, new_p0, p1]
return triangle0, triangle1, triangle2
def get_new_triangles(triangles):
new_triangles = []
for i, triangle in enumerate(triangles):
triangle0, triangle1, triangle2 = make_3triangles_from_triangle(triangles[i])
new_triangles.append(triangle0)
new_triangles.append(triangle1)
new_triangles.append(triangle2)
return new_triangles
せっかくなので周の長さの和と面積を求めてみます。理論的には、周の長さは無限大、面積は0に収束していくはずです。
def get_circumference_and_area(triangles):
distance_between_two_point = abs(triangles[-1][0] - triangles[-1][1])
circumference = len(triangles) * distance_between_two_point
area = math.sqrt(3)/4.0 * distance_between_two_point ** 2
return circumference, area
プログラムを実行してみると周の長さは大きくなっていき、面積は0に収束していく様子が分かります。
depth:0 num_triangles:3 circumference:1.50000 area:0.10825 time:0.000010 [sec]
depth:1 num_triangles:9 circumference:2.25000 area:0.02706 time:0.000118 [sec]
depth:2 num_triangles:27 circumference:3.37500 area:0.00677 time:0.000203 [sec]
depth:3 num_triangles:81 circumference:5.06250 area:0.00169 time:0.000349 [sec]
depth:4 num_triangles:243 circumference:7.59375 area:0.00042 time:0.000826 [sec]
depth:5 num_triangles:729 circumference:11.39062 area:0.00011 time:0.001953 [sec]
depth:6 num_triangles:2187 circumference:17.08594 area:0.00003 time:0.006996 [sec]
depth:7 num_triangles:6561 circumference:25.62891 area:0.00001 time:0.044693 [sec]
depth:8 num_triangles:19683 circumference:38.44336 area:0.00000 time:0.117012 [sec]
depth:9 num_triangles:59049 circumference:57.66504 area:0.00000 time:0.377997 [sec]
drawing...
せっかくなのでアニメーションにしてみました。

ちょっとソースコードを変えてみて、変態なシェルピンスキーのガスケットを作ってみました。

こちらも周の長さは発散して、面積は0に収束します。
ドラゴン曲線
全体のコードはこちら。
下の図のように各ステップで線分の終点を中心に90度回転させた像を足していくとドラゴン曲線と呼ばれる曲線絵が描けます。
点$(x, y)$を点$(C_x, C_y)$を中心に$θ$だけ回転させると点$(x, y)$は
x_{new} = x\cos{\theta} - y\sin{\theta} + C_x - C_x\cos{\theta} + C_y\sin{\theta} \\
y_{new} = x\sin{\theta} + y\cos{\theta} + C_y - C_x\sin{\theta} - C_y\cos{\theta}
に移動します。これを簡単のために
x_{new} = f_x(x,y,C_{x},C_{y}) \\
y_{new} = f_y(x,y,C_{x},C_{y})
と書くことにします。
深さ$j$では新しく$2^j$個の点が出現します。新たに出現する$2^j$個の点を$x_{new}^{(k)}$, $y_{new}^{(k)}$と書くことにします。ただし、$k = 1, 2, … ,2^j$ です。すると、深さ$j$では、各$k$について
x_{new}^{(k)} = f_x(x_{2^j-k},y_{2^j-k},x_{2^j},y_{2^j}) \\
y_{new}^{(k)} = f_y(x_{2^j-k},y_{2^j-k},x_{2^j},y_{2^j})
を計算することで新たに加わる座標を得ることができます。
def get_rotate_coordinate(x, y, Cx, Cy, theta=Pi/2):
newx = x*math.cos(theta)-y*math.sin(theta)+Cx-Cx*math.cos(theta)+Cy*math.sin(theta)
newy = x*math.sin(theta)+y*math.cos(theta)+Cy-Cx*math.sin(theta)-Cy*math.cos(theta)
return newx, newy
def main():
# Initial Condition
xs = [1, 0]
ys = [1, 1]
for depth in range(max_depth):
for k in range(2**depth):
newx, newy = get_rotate_coordinate(xs[2**depth-k-1], ys[2**depth-k-1], Cx=xs[2**depth], Cy=ys[2**depth])
xs.append(newx)
ys.append(newy)
print("depth:{} length:{}".format(depth, len(xs)-1))
print("drawing..")
draw(xs, ys)
こうして得た図が以下です。
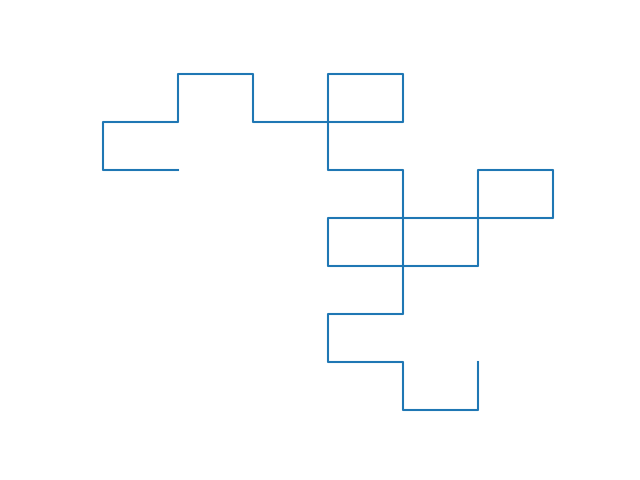 |
 |
 |
|---|---|---|
| depth 5 | depth 10 | depth 20 |
回転角を$\theta=90°$からずらしてみると、ドラゴン曲線の形が連続変形されて行っておもしろいですよ!
