[python]多項式にノイズをのっけてプロット

sin関数に適当にノイズをのせてプロットしたり、make_moonに適当にノイズをのせてプロットしたりといった記事が散見されますが、多項式に適当にノイズをのせてプロットしている記事が見当たらなかったので作りました。

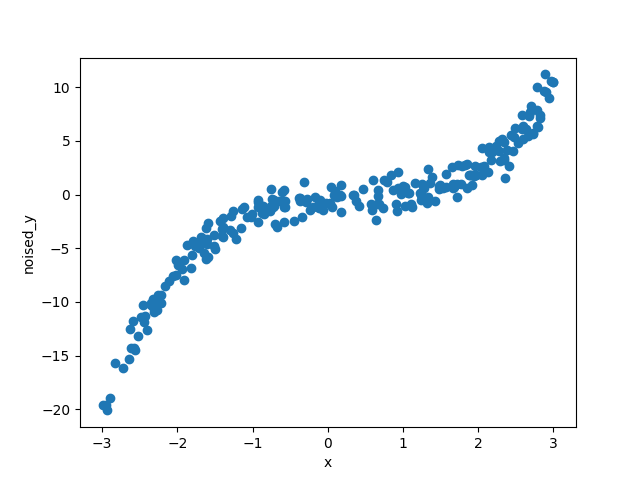
次の例では、$$y=-\frac{1}{2}+\frac{1}{2}x-\frac{1}{2}x^2+\frac{1}{2}x^3$$に適当なノイズを与えてプロットしています。

noise.py

import numpy as np 
import matplotlib.pyplot as plt
import random
import sys

if __name__ == "__main__":

    dim  = +3 #dim次元の多項式の
    number_of_points = 250 #プロットしたい点の数
    xmin = -3 #定義域の最小
    xmax = +3 #定義域の最大
    variance_of_noise = 1 #ノイズの大きさ

    coefficient = [-0.5,0.5,-0.5,0.5] #係数。左から順に0次,1次,2次,3次。

    #多項式の次元の数と、係数の数が一致しない場合は終了。
    if len(coefficient)-1 != dim:
        print("Error.")
        sys.exit()

    x = np.zeros(number_of_points)
    y = np.zeros(number_of_points)
    noised_y = np.zeros(number_of_points)

    for i in range(0,number_of_points):
        x[i] = random.uniform(xmin,xmax)

        for j in range(0,dim+1):
            y[i] = y[i] + coefficient[j]*x[i]**j

        noised_y[i] = np.random.normal(loc=y[i],scale=variance_of_noise)

    plt.scatter(x,noised_y)
    plt.xlabel("x")
    plt.ylabel("noised_y")
    plt.show()

コードの解説

random.uniform(xmin,xmax)

で、xminからxmaxまでの小数をランダムに抽出する。

np.random.normal(loc=y[i],scale=variance_of_noise)

で、y[i]を中心にvariance_of_noise程度の広がりを持つガウシアンからサンプリングする。

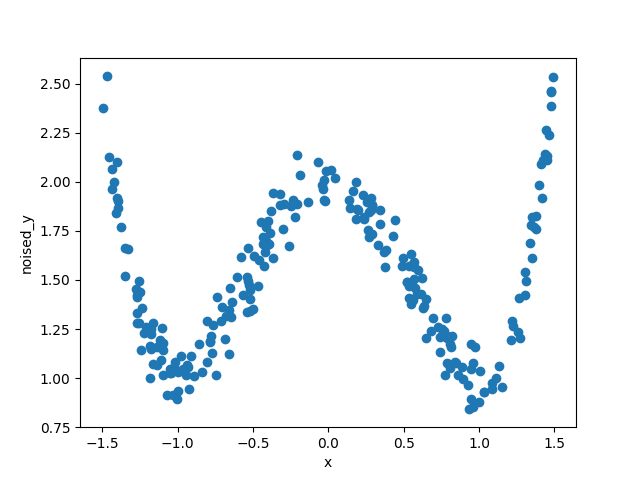
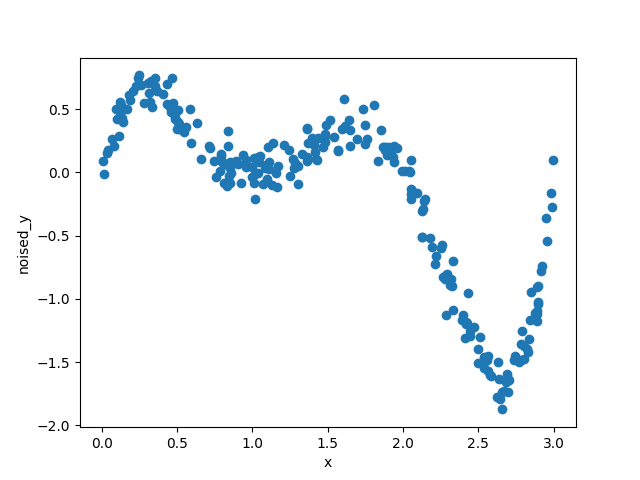
もっと高次元で試してみると…

係数を格納する配列coefficientに過不足なく係数を与えればより何次元の多項式でもOK

例1 $y=x^4-2x^2+2$ ノイズの大きさ0.1

例2 $y=x^5−7x^4+17x^3−17x^2+6x$　ノイズの大きさ0.1