30年ほど長かった平成時代は漸く終わって令和時代に入ったところです。
天文学界隈で前の時代になかった平成時代で始まった新鮮なことというと、太陽系外惑星の探索が代表的な一つでしょう。
昔の人々は星々を見ていながら、その星たちにも太陽と同じようにたくさんな惑星が回っているってことを想像することもあって、太陽系外にある惑星を探す努力はずっと前々からあったが、初めて確実に発見できたのは1995でした。それを始めとしてどんどん発見されてきて、平成時代が終わった時点で発見された系外惑星の数は約4000になっています。
ここではpythonを使って、1995から2019年までの平成時代に発見された系外惑星を簡単に纏めてみます。系外惑星というものに関する説明をしながらpandasやmatplotlibの練習にもなります。
データ取得
系外惑星のデータは色んなサイトから調べられますが、pythonを使ったら手動でサイトからダウンロードする必要もなく、pythonのモジュールでいつでもすぐ天文学のデータを取得できる方法があります。
それはastroqueryというモジュールです。astroqueryは天文学で広く使われているモジュールであるastropyの付属モジュールです。これを使うとサイトから色んな天文学のデータと接続することができるのです。
pipやcondaで簡単にインストールできます。
pip install --pre astroquery
conda install -c astropy astroquery
ここで使うのはNasaExoplanetArchiveというデータベースです。名前の通り系外惑星(exoplanet)のデータが格納されています。
詳しくはこのサイトでhttps://exoplanetarchive.ipac.caltech.edu/index.html
データはこのサイトから検索したりダウンロードしたりできますが、astroqueryを使ったらすぐ確認されたすべての系外惑星のデータをダウンロードして、自分で分析や可視化に使うことができます。
from astroquery.nasa_exoplanet_archive import NasaExoplanetArchive
# これらのモジュールもこれから使うので予めインポート
import numpy as np
import pandas as pd
import matplotlib as mpl
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
table = NasaExoplanetArchive.get_confirmed_planets_table()
print(table)
pl_hostname pl_letter pl_name ... NAME_LOWERCASE sky_coord
... deg,deg
------------ --------- -------------- ... -------------- ---------------------
Kepler-92 b Kepler-92 b ... kepler-92b 289.086058,41.562941
Kepler-92 c Kepler-92 c ... kepler-92c 289.086058,41.562941
Kepler-93 b Kepler-93 b ... kepler-93b 291.418281,38.672354
Kepler-93 c Kepler-93 c ... kepler-93c 291.418281,38.672354
Kepler-94 b Kepler-94 b ... kepler-94b 281.194747,47.497148
Kepler-94 c Kepler-94 c ... kepler-94c 281.194747,47.497148
... ... ... ... ... ...
K2-256 b K2-256 b ... k2-256b 186.227158,-2.065931
K2-257 b K2-257 b ... k2-257b 188.278488,-1.953159
K2-258 b K2-258 b ... k2-258b 187.631332,-1.16092
K2-259 b K2-259 b ... k2-259b 186.802689,1.566849
IC 4651 9122 b IC 4651 9122 b ... ic46519122b 261.208618,-49.948917
HD 26965 b HD 26965 b ... hd26965b 63.818001,-7.652871
Wolf 503 b Wolf 503 b ... wolf503b 206.847687,-6.136875
Length = 3946 rows
見ての通り、確認された系外惑星が3946もあります。これはすでにこのサイトに載ったデータだけで、全部っていうわけではないかもしれません。
サイトによって系外惑星のデータがちょっと違うことがあります。http://exoplanet.eu の方がちょっとデータが多いようです。
ここで扱うデータは令和元年5月1日0:13時(日本時間)に取得したものです。
ただしこれを使ったらデータが保存されて、次回からはダウンロードすることなく、ただ保存されたデータを読み出すだけとなります。それは早いですが、系外惑星のデータは常に更新されています。いつも最新のデータを得るために毎回改めてダウンロードした方がいいです。
cache=0をつけることで最新データが得られます。
table = NasaExoplanetArchive.get_confirmed_planets_table(cache=0)
get_confirmed_planets_tableを使ったら確認された惑星のデータは貰えますが、それはastropyのQTableであり、ちょっと扱いにくいので、ここではデータサイエンティストの馴染んでいるpandasのDataFrameに変換します。
df = pd.DataFrame({c: table[c] for c in table.columns})
df.set_index('pl_name',inplace=True)
print(df.columns.values)
print(df.shape)
['pl_hostname' 'pl_letter' 'pl_discmethod' 'pl_controvflag' 'pl_pnum'
'pl_orbper' 'pl_orbpererr1' 'pl_orbpererr2' 'pl_orbperlim' 'pl_orbpern'
'pl_orbsmax' 'pl_orbsmaxerr1' 'pl_orbsmaxerr2' 'pl_orbsmaxlim'
'pl_orbsmaxn' 'pl_orbeccen' 'pl_orbeccenerr1' 'pl_orbeccenerr2'
'pl_orbeccenlim' 'pl_orbeccenn' 'pl_orbincl' 'pl_orbinclerr1'
'pl_orbinclerr2' 'pl_orbincllim' 'pl_orbincln' 'pl_bmassj'
'pl_bmassjerr1' 'pl_bmassjerr2' 'pl_bmassjlim' 'pl_bmassn' 'pl_bmassprov'
'pl_radj' 'pl_radjerr1' 'pl_radjerr2' 'pl_radjlim' 'pl_radn' 'pl_dens'
'pl_denserr1' 'pl_denserr2' 'pl_denslim' 'pl_densn' 'pl_ttvflag'
'pl_kepflag' 'pl_k2flag' 'ra_str' 'dec_str' 'ra' 'st_raerr' 'dec'
'st_decerr' 'st_posn' 'st_dist' 'st_disterr1' 'st_disterr2' 'st_distlim'
'st_distn' 'st_optmag' 'st_optmagerr' 'st_optmaglim' 'st_optband'
'gaia_gmag' 'gaia_gmagerr' 'gaia_gmaglim' 'st_teff' 'st_tefferr1'
'st_tefferr2' 'st_tefflim' 'st_teffn' 'st_mass' 'st_masserr1'
'st_masserr2' 'st_masslim' 'st_massn' 'st_rad' 'st_raderr1' 'st_raderr2'
'st_radlim' 'st_radn' 'pl_nnotes' 'rowupdate' 'pl_facility'
'NAME_LOWERCASE' 'sky_coord']
(3946, 83)
データは84列ありますが、ここで惑星の名前であるpl_name列をインデックスにして残りは83列となります。
各列の意味はこのサイトに説明してあります。https://exoplanetarchive.ipac.caltech.edu/docs/API_exoplanet_columns.html
これからこのデータを使って解説していきます。
系外惑星の発見方法
まず系外惑星ってどうやって発見するものなのか興味深いですね。
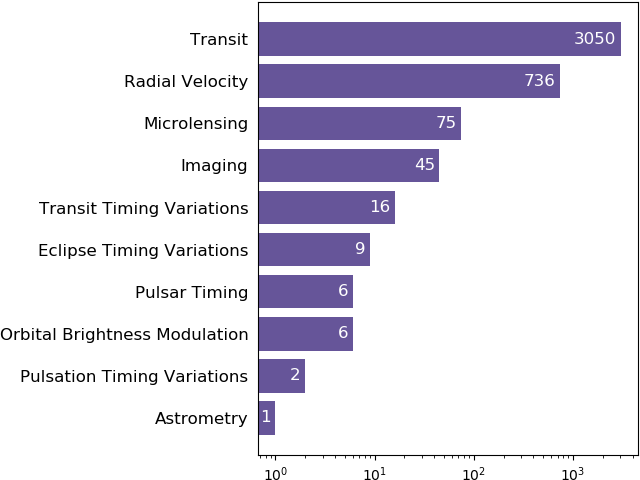
各惑星の発見方法はpl_discmethod列に書いてあります。ここで各方法で発見された惑星の数を纏めてみます。
n_discmet = df.groupby('pl_discmethod').apply(len).sort_values(ascending=False)
lis_discmet = n_discmet.index
for i,(dm,n) in enumerate(n_discmet.iteritems()):
plt.text(n*0.9,i,'%d'%n,fontsize=12,ha='right',va='center',color='w')
n_met = len(n_discmet)
plt.barh(range(n_met),n_discmet,color='#665599')
plt.yticks(range(n_met),lis_discmet,fontsize=12)
plt.semilogx()
plt.tick_params(left=0)
plt.gca().invert_yaxis()
plt.tight_layout(0)
plt.show()
各方法の詳しくはwikiとかで読めます。https://ja.wikipedia.org/wiki/太陽系外惑星の発見方法
ここでは最も有効な6つの方法をちょっと手短に説明します。
Transit = トランジット法
現在で一番他の方法より遥かに成果を出している方法です。惑星が主星の手前を通過している時にその主星の見かけの光度はやや下がって、時間と光度のグラフを描いたら凹みが見えて、惑星があると推測できます。
惑星が大きければ大きいほど凹みが大きいため、光度のグラフを見たら惑星の大きさは測定できます。光度の最大変化は大体大きさの比率の平方数となります。つまり、$\left(r_p/r_s\right)^2$。
ここで$r_p$は惑星の大きさで、$r_s$は主星の大きさです。ただしこれは完全に主星が惑星の後ろにある場合だけで、軌道傾斜角がちょっと大きい場合は少ししか光度が減らなくて、観測はもっと難しくなります。
勿論この方法の大きな短所は惑星の軌道が地球から見てほぼちょうど垂線でないと通過はしないので見つけようがないのです。
Radial Velocity = 視線速度法
惑星が主星の重力で公転している時に実は主星もやや動きます。その動きはほんの僅かで見えることはできないが、ドップラー効果によってスペクトル線の変化が起こります。その変化を観測することで惑星が存在すると推測できます。
惑星が重ければ重いほどスペクトル線の変化が大きいため、そこから惑星の質量を推測できます。
この方法では軌道傾斜角が大きければ探せやすいが、トランジット法みたいに垂線でなくてもいいので、探せる惑星の範囲はトランジット法より大きい。
Microlensing = 重力マイクロレンズ法
目標の恒星の後ろ(背景)にある天体の重力レンズ効果による歪みを観測することでその恒星の周りにある惑星の存在は推測できます。惑星があると重力レンズによる歪みが惑星がない場合とは違うからです。
この方法では遠くにある星には他の方法より有効ですが、背景にある天体がないと使えないので、ほとんどは特に星が集まっている銀河の中心しか使えません。
Imaging = 直接観測法
直接望遠鏡で惑星の写真を撮ることです。最も単純でわかりやすい方法ですが、実際に惑星は主星より遥かに暗いのであまり簡単ではありません。主星の光を隠すコロナグラフと随分解像度の高い撮影が必要とされます。小さい惑星を撮影することは至難です。
惑星の姿は主星の眩しさによって隠蔽されやすいため、主星から離れている惑星の方が探しやすいです。
Transit Timing Variations = トランジット時間変動
先に発見された惑星の通過する時間がもう一つの惑星の影響によって変動することがあります。その変動を観測することでもう一つの惑星があると推測できます。
Eclipse Timing Variations = 食の時間変動
トランジット時間変動と似ていますが、惑星ではなく、二つの恒星のお互いに通過する時間の変動を観測することです。
発見に使った観測装置
系外惑星が探せる観測装置がたくさんあります。地上の天文台も宇宙望遠鏡も使えます。各惑星を見つけた天文台や望遠鏡の名前はpl_facility列に書いてあります。
n_fac_dis = df.groupby('pl_facility').apply(len).sort_values(ascending=False)
print(n_fac_dis)
pl_facility
Kepler 2342
K2 360
La Silla Observatory 232
W. M. Keck Observatory 171
Multiple Observatories 116
SuperWASP 110
HATNet 57
HATSouth 57
OGLE 50
Haute-Provence Observatory 45
Anglo-Australian Telescope 35
SuperWASP-South 32
Lick Observatory 32
CoRoT 31
McDonald Observatory 28
MOA 23
Okayama Astrophysical Observatory 23
Paranal Observatory 17
Roque de los Muchachos Observatory 17
Bohyunsan Optical Astronomical Observatory 16
Las Campanas Observatory 14
Transiting Exoplanet Survey Satellite (TESS) 11
KELT 10
Gemini Observatory 9
Subaru Telescope 8
Thueringer Landessternwarte Tautenburg 8
Qatar 7
KMTNet 7
Multiple Facilities 7
Hubble Space Telescope 6
Fred Lawrence Whipple Observatory 6
XO 6
Calar Alto Observatory 5
TrES 5
KELT-North 5
KELT-South 4
Spitzer Space Telescope 3
Arecibo Observatory 3
United Kingdom Infrared Telescope 2
SuperWASP-North 2
Palomar Observatory 2
Parkes Observatory 2
Large Binocular Telescope Observatory 2
Cerro Tololo Inter-American Observatory 2
Xinglong Station 2
MEarth Project 2
Apache Point Observatory 1
European Southern Observatory 1
Yunnan Astronomical Observatory 1
Infrared Survey Facility 1
Kitt Peak National Observatory 1
Leoncito Astronomical Complex 1
Mauna Kea Observatory 1
Oak Ridge Observatory 1
Teide Observatory 1
WASP-South 1
Acton Sky Portal Observatory 1
dtype: int64
これを見ると半分以上の発見はケプラー宇宙望遠鏡の実績だとわかります。ケプラーはトランジット法で系外惑星を探すために2009年3月6日に宇宙に打ち上げられ、2018年10月30日に退役した宇宙望遠鏡です。2009年から2013年までのケプラーは健全な状態で働いていましたが、その後2つめのリアクションホイールが故障したことで2014年からK2に名称を変えて劣化した状態で観測を続けてきました。
このデータの中では別々に「Kepler」は2009年から2013年までのケプラーを示して、「K2」は後期のケプラーを示します。K2は初期のケプラーより随分劣ったが、それでもたくさん新しい惑星を発見できました。
トランジット系外惑星探索衛星(TESS)はケプラーの後継者であり、2018年4月18日から打ち上げられたばかりで、これからはケプラーと同じような実績を積んでいくでしょう。
地上の天文台では、チリのアタカマ砂漠にあるラ・シヤ天文台(La Silla Observatory)が一番です。
色んなところの望遠鏡を共に使って発見された惑星も少なくないです。
日本では岡山天体物理観測所では視線速度法による惑星探しも行なっています。
print(df[df.pl_facility=='Okayama Astrophysical Observatory'].index.values)
['HD 14067 b' '6 Lyn b' '14 And b' '18 Del b' '75 Cet b' '81 Cet b'
'HD 81688 b' 'eps Tau b' 'nu Oph b' 'nu Oph c' 'ome Ser b' 'omi CrB b'
'omi UMa b' 'xi Aql b' 'HD 104985 b' 'HD 120084 b' 'HD 2952 b'
'HD 5608 b' 'gam Lib b' 'gam Lib c' '24 Boo b' 'HD 47366 b' 'HD 47366 c']
その他にすばる望遠鏡はハワイのマウナ・ケア山にあるが日本の望遠鏡です。惑星を視線速度法及び直接観測法によって発見しています。
print(df[df.pl_facility=='Subaru Telescope'].pl_discmethod)
pl_name
HD 17156 b Radial Velocity
HD 38801 b Radial Velocity
kap And b Imaging
DH Tau b Imaging
GJ 504 b Imaging
HD 145457 b Radial Velocity
HD 149026 b Radial Velocity
HD 180314 b Radial Velocity
Name: pl_discmethod, dtype: object
惑星の大きさ
惑星の大きさはpl_radj列に、主星である恒星の大きさはst_rad列に書いてあります。ただし、惑星の大きさの単位は木星の倍数で、主星のは太陽の倍数です。
単位は倍数なので大きさと言っても半径と言っても直径と言ってもほぼ同じ意味となります。
まだ大きさが測定されていない惑星もあります。データがない場合は0と表記されるので、まずはそれを除外してから分析します。
df1 = df[df.pl_radj>0]
print(df1.pl_radj.describe())
count 3080.000000
mean 0.370629
std 0.422444
min 0.030000
25% 0.140000
50% 0.208000
75% 0.315000
max 6.900000
Name: pl_radj, dtype: float64
3946の中で大きさをわかる惑星は3080あります。
視線速度法や重力マイクロレンズ法によって発見された惑星は大きさを測定することができません。ただし視線速度法で発見された後に他の方法で観測して大きさを測定することができますが、重力マイクロレンズ法で発見された惑星は大体他の方法で観測することができないため、大きさをわかる惑星は一つもありません。
大きさをわかる惑星だけに絞った後、各方法で発見された数を見ます。
print(df1.groupby('pl_discmethod').apply(len).sort_values(ascending=False))
pl_discmethod
Transit 3042
Imaging 15
Radial Velocity 13
Transit Timing Variations 7
Orbital Brightness Modulation 3
dtype: int64
一番小さいと大きい惑星の名前を見ます。
print(df1.loc[[df1.pl_radj.idxmin(),df1.pl_radj.idxmax()]].pl_radj)
pl_name
Kepler-37 b 0.03
HD 100546 b 6.90
Name: pl_radj, dtype: float64
一番大きいHD 100546 bは木星の6.9倍くらい大きいです。木星より大きい惑星がたくさんありますが、大きすぎると褐色矮星に見なされることがあるので限界があります。褐色矮星は最も小さいタイプの恒星であり、巨大惑星と混同しやすいです。
地球の大きさは木星の0.08921倍です。一番小さいKepler-37 bは木星の0.03倍、つまり地球の0.354倍くらいしかないのです。太陽系で一番小さい惑星である水星は地球の0.383倍です。今まで発見された系外惑星の中で水星よりも小さいのはKepler-37 bしかないのです。
発見された惑星の中で地球より小さい惑星も少なくないです。どれくらい木星より大きい惑星と地球より小さい惑星があるか見てみましょう。
print((df1.pl_radj>1).sum()) # 木星より大きい惑星の数
print((df1.pl_radj<0.08921).sum()) # 地球より小さい惑星の数
387
157
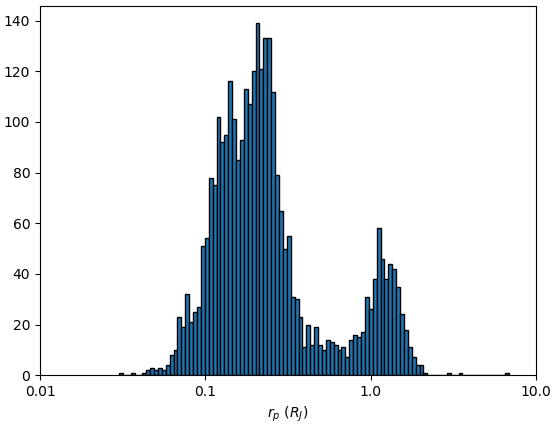
惑星の大きさの分布
plt.hist(np.log10(df1.pl_radj),100,ec='k')
plt.xlabel('$r_p$ ($R_J$)')
xtick = np.arange(-2,2.)
plt.xticks(xtick,10**xtick)
plt.show()
主星の大きさ
次は主星の大きさを見ます。
st_rad = df[df.st_rad>0].drop_duplicates('pl_hostname').st_rad
print(st_rad.describe())
count 2720.000000
mean 1.689048
std 4.083175
min 0.040000
25% 0.810000
50% 0.990000
75% 1.280000
max 71.230000
Name: st_rad, dtype: float64
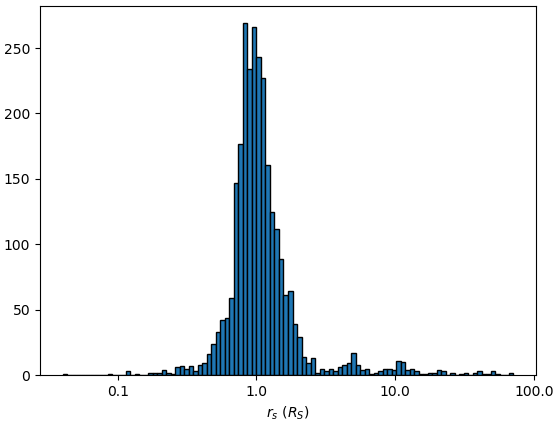
主星の大きさの分布。
plt.hist(np.log10(st_rad),100,ec='k')
plt.xlabel('$r_s$ ($R_S$)')
xtick = np.arange(-1,3.)
plt.xticks(xtick,10**xtick)
plt.show()
主星に対する惑星の大きさ
次は惑星と主星の大きさを比べてみますが、まず同じような単位に変換します。木星の半径は太陽の0.10049倍なので。
df1 = df[(df.pl_radj>0)&(df.st_rad>0)]
pl_rad = df1.pl_radj*0.10049
st_rad = df1.st_rad
rp_rs = pl_rad / st_rad
print(rp_rs.describe())
count 3070.000000
mean 0.036103
std 0.041042
min 0.003816
25% 0.015219
50% 0.023031
75% 0.035952
max 1.042863
dtype: float64
一番比率の高い惑星は主星よりもやや大きいです。これは特に大きい惑星ではなく、主星の方が特に小さい褐色矮星です。
df2 = pd.DataFrame({'rp': pl_rad, 'rs': st_rad, 'rp_rs': rp_rs})
print(df2.loc[[rp_rs.idxmin(),rp_rs.idxmax()]])
rp rs rp_rs
pl_name
Kepler-37 b 0.003015 0.79 0.003816
WISEP J121756.91+162640.2 A b 0.093858 0.09 1.042863
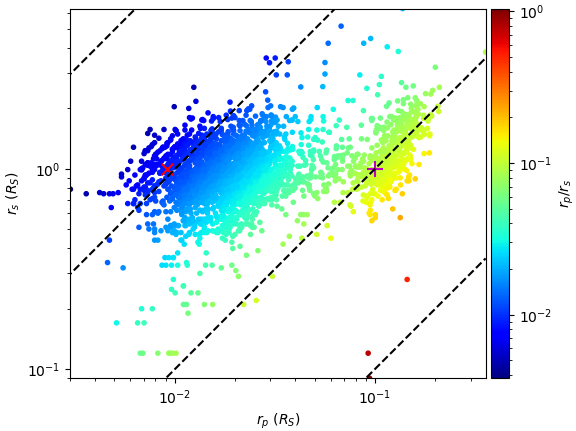
惑星と主星の大きさの分布を見ます。比較するために、地球と木星も入れられます。
plt.gca(xlim=[pl_rad.min(),pl_rad.max()],ylim=[st_rad.min(),st_rad.max()],aspect=1)
x = np.array([0,pl_rad.max()])
for r in np.logspace(-3,0,4):
plt.plot(x,x/r,'k--')
plt.scatter(pl_rad,st_rad,c=rp_rs,norm=mpl.colors.LogNorm(),marker='.',cmap='jet')
plt.xlabel('$r_p$ ($R_S$)')
plt.ylabel('$r_s$ ($R_S$)')
plt.colorbar(pad=0.01,label='$r_p/r_s$')
plt.scatter([0.0091577],[1],70,c='r',marker='x')
plt.scatter([0.10049],[1],140,c='m',marker='+')
plt.loglog()
plt.show()
左の方の×は地球で、右の方の+は木星。
面白いことに、惑星の大きさは大まかに地球に近い団体と木星に近い団体に二つ分けられているようです。
公転周期
惑星の公転周期はpl_orbper列に書いてあります。単位は日数。
pl_orbper = df[(df.pl_orbper>0)].pl_orbper
print(pl_orbper.describe())
count 3.842000e+03
mean 2.357470e+03
std 1.181497e+05
min 9.070629e-02
25% 4.567262e+00
50% 1.198999e+01
75% 4.237136e+01
max 7.300000e+06
Name: pl_orbper, dtype: float64
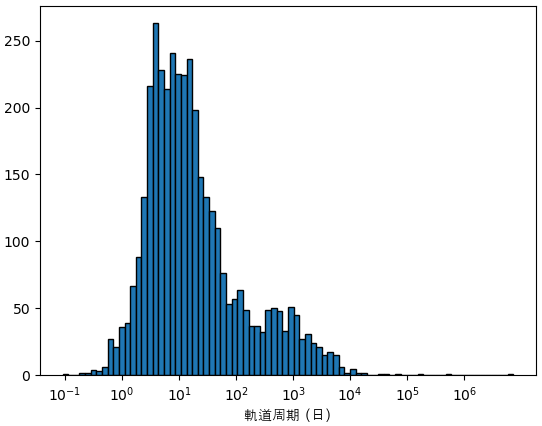
分布
plt.hist(np.log10(pl_orbper),80,ec='k')
plt.xlabel('軌道周期 (日)',fontname='AppleGothic')
xtick = np.arange(-1,7.)
plt.xticks(xtick,['$10^{%d}$'%x for x in xtick])
plt.show()
公転周期が短いほど惑星がよく主星を通過するし、主星に近いほど主星に与える重力も大きいため、視線速度法とトランジット法では探せやすいので、短い公転周期を持つ惑星がたくさん見つかっています。
太陽系では一番公転周期が短い水星でも87.969日です。つまり今発見された系外惑星の大半は太陽系の基準より小さい軌道の持っています。これは発見のバイアスでもありますが、太陽系とは全然違う惑星系がこんなにたくさん存在することは判明です。
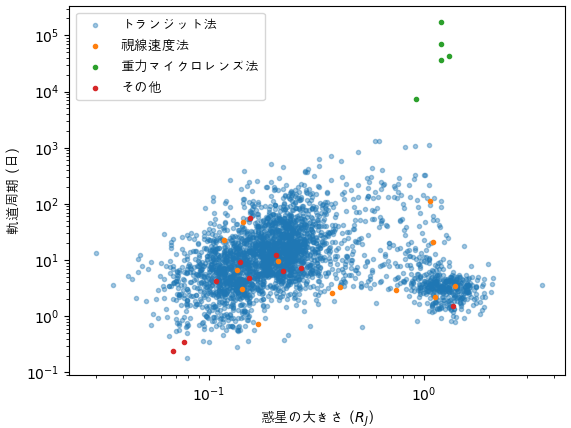
各方法で発見された惑星の大きさと公転周期を見ます。
df1 = df[(df.pl_radj>0)&(df.pl_orbper>0)]
print(len(df1))
df2 = df1[df1.pl_discmethod=='Transit']
plt.scatter(df2.pl_radj,df2.pl_orbper,marker='.',alpha=0.4)
df2 = df1[df1.pl_discmethod=='Radial Velocity']
plt.scatter(df2.pl_radj,df2.pl_orbper,marker='.')
df2 = df1[df1.pl_discmethod=='Imaging']
plt.scatter(df2.pl_radj,df2.pl_orbper,marker='.')
df2 = df1[(df1.pl_discmethod!='Transit')&(df1.pl_discmethod!='Radial Velocity')&(df1.pl_discmethod!='Imaging')]
plt.scatter(df2.pl_radj,df2.pl_orbper,marker='.')
plt.xlabel('惑星の大きさ ($R_J$)',fontname='AppleGothic')
plt.ylabel('軌道周期 (日)',fontname='AppleGothic')
plt.legend(['トランジット法','視線速度法','重力マイクロレンズ法','その他'],prop={'family':'AppleGothic'})
plt.loglog()
plt.show()
視線速度法とトランジット法によって見つかった惑星の軌道周期が短いのに対し、直接観測法によって見つかった惑星は軌道周期が長くて、大きいものばかりってことはわかります。
惑星の軌道傾斜角
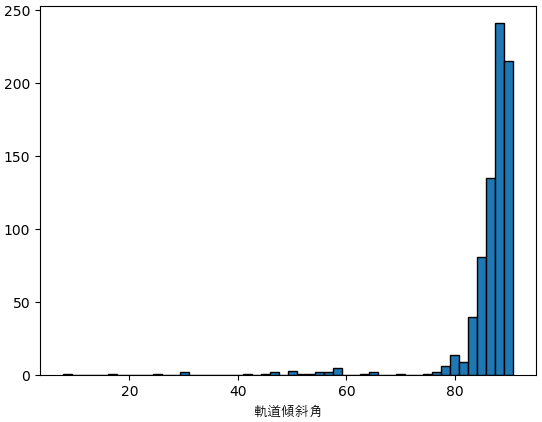
惑星の軌道傾斜角はpl_orbincl列に書いてありますが、データのあるものが少ないです。
垂直に近い角度ではトランジット法で観測されやすいので、80~90度の辺りに集まっています。
pl_orbincl = df[(df.pl_orbincl>0)].pl_orbincl
print(pl_orbincl.describe())
plt.hist(pl_orbincl,50,ec='k')
plt.xlabel('軌道傾斜角',fontname='AppleGothic')
plt.show()
count 771.000000
mean 86.100313
std 7.956823
min 7.700000
25% 86.010000
50% 88.010000
75% 89.210000
max 90.760000
Name: pl_orbincl, dtype: float64
惑星の質量
惑星の質量はpl_bmassj列に書いてありますが、これ列のデータの一部はすべて実際の質量ではなく、ただの下限質量です。つまり質量かける軌道傾斜角の正弦
$M*sin(i)$
ここで$i$は軌道傾斜角で、$M$は実際の質量です。単位は木星の質量の倍数。
視線速度法で発見された惑星の質量を求める一般な方法としてドップラー効果の測定が使われています。スペクトルの変動は質量によりますが、その他に軌道傾斜角にもよります。だから測定できるのは$M*sin(i)$で、軌道傾斜角が大きければ大きいほど実際の質量はその値より大きいことになります。
pl_bmassprov列を調べれば、下限質量であるものは「Msini」と書いてあります。
視線速度法で発見された惑星の軌道傾斜角がわからなければ実際の質量がわからず下限質量しかわからないが、軌道傾斜角がわかるものはpl_bmassprov列に「Msin(i)/sin(i)」と表記され、質量も実際の質量になっています。
他の方法で質量を取得する場合、pl_bmassprov列に「Mass」と表記されます。
df1 = df[(df.pl_bmassj>0)]
print(df1.pl_bmassj.describe())
print(df.groupby('pl_bmassprov').apply(len))
count 1530.000000
mean 2.535104
std 4.431595
min 0.000060
25% 0.110840
50% 0.915500
75% 2.580000
max 55.590000
Name: pl_bmassj, dtype: float64
pl_bmassprov
Mass 824
Msin(i)/sin(i) 5
Msini 701
dtype: int64
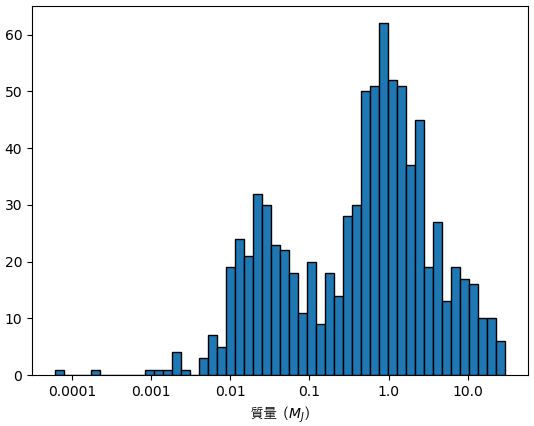
実際の質量をわかる惑星だけの質量分布を見ます。
df1 = df[(df.pl_bmassj>0)&(df.pl_bmassprov!='Msini')]
print(df1.pl_bmassj.describe())
plt.hist(np.log10(df1.pl_bmassj),50,ec='k')
plt.xlabel('質量 ($M_J$)',fontname='AppleGothic')
xtick = np.arange(-4,2.)
plt.xticks(xtick,10**xtick)
plt.show()
count 829.000000
mean 2.072610
std 4.088909
min 0.000060
25% 0.069220
50% 0.650000
75% 1.855000
max 30.000000
Name: pl_bmassj, dtype: float64
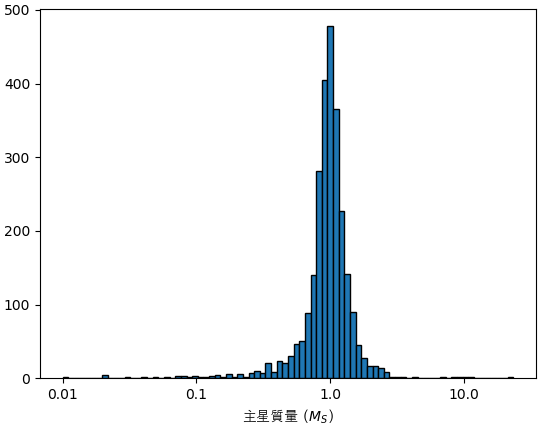
主星の質量
主星の質量はst_mass列に書いてあります。単位は太陽質量の倍数。
st_mass = df[df.st_mass>0].drop_duplicates('pl_hostname').st_mass
print(st_mass.describe())
plt.hist(np.log10(st_mass),80,ec='k')
plt.xlabel('主星質量 ($M_S$)',fontname='AppleGothic')
xtick = np.arange(-2,2.)
plt.xticks(xtick,10**xtick)
plt.show()
count 2633.000000
mean 1.027626
std 0.678201
min 0.010000
25% 0.830000
50% 0.980000
75% 1.140000
max 23.560000
Name: st_mass, dtype: float64
主星の中で太陽と同じくらいの質量を持つ恒星が多いです。
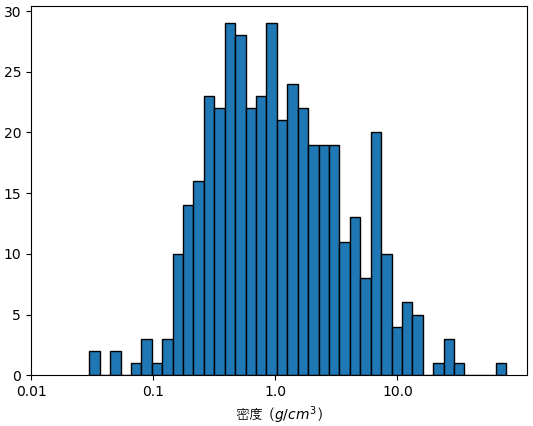
惑星の密度
惑星の密度はpl_densに書かれていますが、密度データのある惑星は少ないし、不確定性も大きいです。密度の誤差はpl_denserr1列とpl_denserr2列に書いてあります。
df1 = df[df.pl_dens>0]
print(df1.pl_dens.describe())
print(df1.loc[[df1.pl_dens.idxmin(),df1.pl_dens.idxmax()]][['pl_dens','pl_denserr1','pl_denserr2']])
plt.hist(np.log10(df1.pl_dens),40,ec='k')
plt.xlabel('密度 ($g/cm^3$)',fontname='AppleGothic')
xtick = np.arange(-2,2.)
plt.xticks(xtick,10**xtick)
plt.show()
count 435.000000
mean 2.509603
std 5.200267
min 0.030000
25% 0.410000
50% 0.964000
75% 2.500000
max 77.700000
Name: pl_dens, dtype: float64
pl_dens pl_denserr1 pl_denserr2
pl_name
Kepler-51 b 0.03 0.02 -0.01
Kepler-131 c 77.70 55.00 -55.00
一番密度の高い惑星は$77.7 g/cm^3$ほど高いですが、$\pm55.0$ だからあまり不確定です。
天球上の位置
星の天球上の位置を示す赤緯と赤経はra列とdec列に書いてあります。単位は度。
星空を見たらどんな方向もいっぱい星が見えるから、系外惑星の観測も空のいたるところで行なっていますが、観測方法によるバイアスがあります。
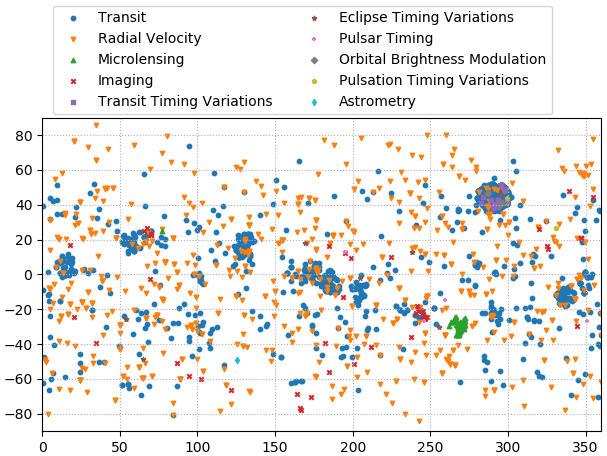
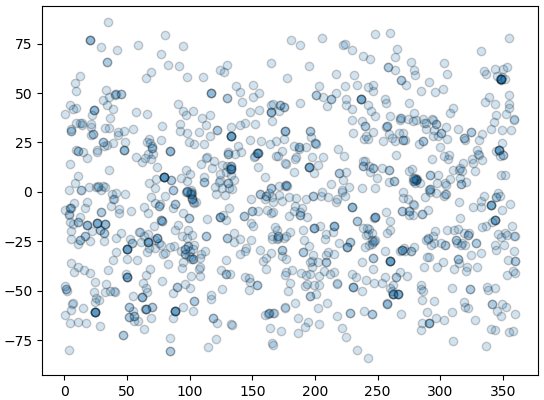
方法別で星の位置を調べてみましょう。
marker = ['o','v','^','x','s','*','+','D','p','d']
plt.gca(xlim=[0,360],ylim=[-90,90])
for d,m in zip(lis_discmet,marker):
plt.scatter(df.ra[df.pl_discmethod==d],df.dec[df.pl_discmethod==d],s=10,marker=m)
plt.legend(lis_discmet,loc=(0.02,1.01),ncol=2)
plt.grid(ls=':')
plt.tight_layout()
plt.show()
視線速度法のはほとんど同じ分布ですが、トランジット法と重力マイクロレンズ法はある特定なところにたくさん集まっています。
その原因は、重力マイクロレンズ法は特に星がたくさん集っている場所である銀河の中心に向かう方向に特別有効な方法だからです。
トランジット法自体はそんなにバイアスがないが、ケプラーは選ばれた特定な辺りしか観測しないので、ケプラーの観測の範囲では非常に集まります。
初期のケプラーはずっとはくちょう座の小さな方角だけ観測していたが、K2では黄道の近くに対象を変えました。
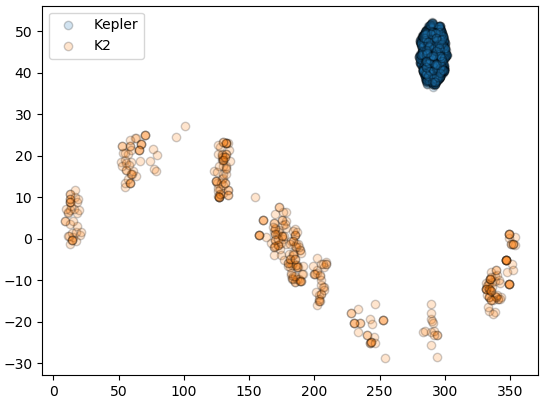
このデータではpl_kepflagとpl_k2flagという列があります。それはケプラーとK2の観測対象であるかどうかというフラグです。(0=否、1=是)
そのフラグがついている惑星がある特定に位置しか分布しないのです。
df_k = df[df.pl_kepflag==1]
plt.scatter(df_k.ra,df_k.dec,edgecolor='k',alpha=0.2)
df_k2 = df[df.pl_k2flag==1]
plt.scatter(df_k2.ra,df_k2.dec,edgecolor='k',alpha=0.2)
plt.legend(['Kepler','K2'])
plt.show()
つまり、今まで発見された惑星の大半はケプラーの観測対象であるはくちょう座にあります。
ケプラーのフラグを持つ惑星と、マイクロレンズ法によって見つかった惑星を除外したら特に集る辺りはほぼ消えています。
df1 = df[df.pl_kepflag+df.pl_k2flag+(df.pl_discmethod=='Microlensing')==0]
plt.scatter(df1.ra,df1.dec,edgecolor='k',alpha=0.2)
plt.show()
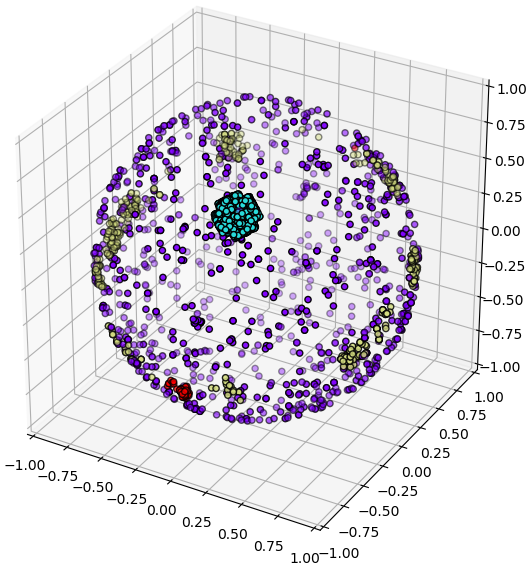
赤緯と赤経から三次元の天球に変換して、分布を見ることもできます。
x = np.cos(np.radians(df.dec))*np.cos(np.radians(df.ra))
y = np.cos(np.radians(df.dec))*np.sin(np.radians(df.ra))
z = np.sin(np.radians(df.dec))
plt.figure(figsize=[6,6])
ax = plt.axes([0,0,1,1],projection='3d',xlim=[-1,1],ylim=[-1,1],zlim=[-1,1])
c = (df.pl_discmethod=='Microlensing')*3+df.pl_kepflag+df.pl_k2flag*2
ax.scatter(x,y,z,c=c,edgecolor='k',cmap='rainbow')
plt.show()
ここで水色と灰色はケプラーとK2の観測対象で、赤色はマイクロレンズ法で発見されたものです。
地球からの距離
惑星系の地球からの距離はパーセク(pc)単位でst_dist列に書いてあります。
df1 = df[df.st_dist>0].drop_duplicates('pl_hostname')
print(df1.st_dist.describe())
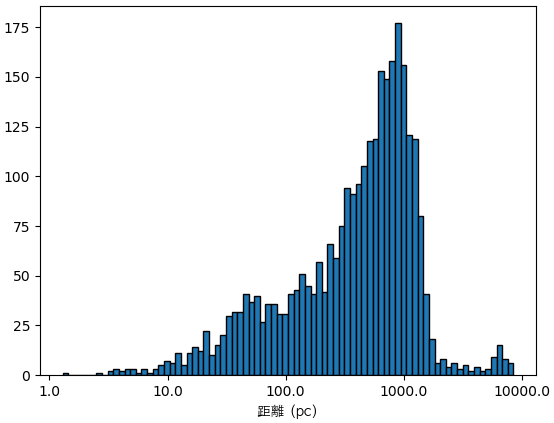
plt.hist(np.log10(df1.st_dist),80,ec='k')
plt.xlabel('距離 (pc)',fontname='AppleGothic')
xtick = np.arange(4.)
plt.xticks(xtick,10**xtick)
plt.show()
count 2930.000000
mean 658.883689
std 875.723167
min 1.290000
25% 171.000000
50% 499.000000
75% 872.000000
max 8500.000000
Name: st_dist, dtype: float64
球体の面積が半径の平方なので、遠いほどたくさん星がありますが、遠すぎるとよく見えないため、最も惑星が発見されたのは1000pcくらいのところです。
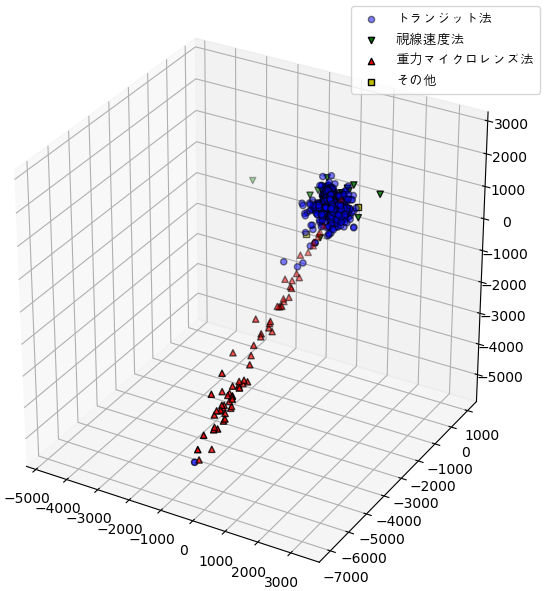
距離と赤緯と赤経を合わせたら三次元空間での分布を表現することができます。
x = np.cos(np.radians(df1.dec))*np.cos(np.radians(df1.ra))*df1.st_dist
y = np.cos(np.radians(df1.dec))*np.sin(np.radians(df1.ra))*df1.st_dist
z = np.sin(np.radians(df1.dec))*df1.st_dist
a,b,c = np.array([x.max()+x.min(),y.max()+y.min(),z.max()+z.min()])/2
m = max([x.max()-x.min(),y.max()-y.min(),z.max()-z.min()])/2
plt.figure(figsize=[6,6])
ax = plt.axes([0,0,1,1],projection='3d',xlim=[a-m,a+m],ylim=[b-m,b+m],zlim=[c-m,c+m])
c = df1.pl_discmethod=='Transit'
ax.scatter(x[c],y[c],z[c],c='b',edgecolor='k',cmap='rainbow',marker='o',alpha=0.5)
c = df1.pl_discmethod=='Radial Velocity'
ax.scatter(x[c],y[c],z[c],c='g',edgecolor='k',cmap='rainbow',marker='v',)
c = df1.pl_discmethod=='Microlensing'
ax.scatter(x[c],y[c],z[c],c='r',edgecolor='k',cmap='rainbow',marker='^')
c = (df1.pl_discmethod!='Transit')&\
(df1.pl_discmethod!='Radial Velocity')&\
(df1.pl_discmethod!='Microlensing')
ax.scatter(x[c],y[c],z[c],c='y',edgecolor='k',cmap='rainbow',marker='s')
plt.legend(['トランジット法','視線速度法','重力マイクロレンズ法','その他'],prop={'family':'AppleGothic'})
plt.show()
大部分は1000pc以内に集まっていますが、銀河の中心の方向には重力マイクロレンズ法で発見された惑星が距離ばらばらで幅広く分布しています。
主星の等級
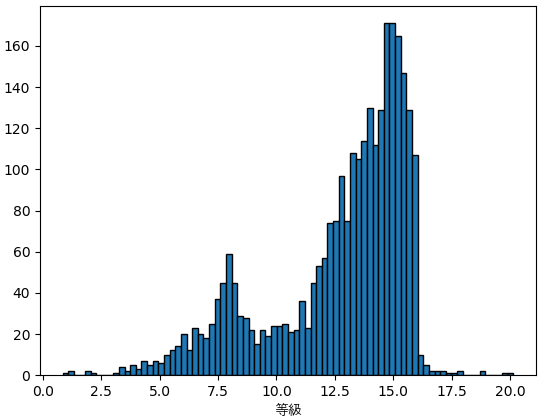
地球から見える主星の明るさを示す等級はst_optmagに書いてあります。この数値が小さいほど明るいです。
df1 = df[df.st_optmag>0].drop_duplicates('pl_hostname')
print(df1.st_optmag.describe())
plt.hist(df1.st_optmag,80,ec='k')
plt.xlabel('等級',fontname='AppleGothic')
plt.show()
count 2789.000000
mean 12.694392
std 2.965030
min 0.850000
25% 11.472000
50% 13.659000
75% 14.935000
max 20.150000
Name: st_optmag, dtype: float64
等級の低い星は大体よく知っている有名な星です。
st_optmag = df[df.st_optmag!=0].drop_duplicates('pl_hostname').set_index('pl_hostname').sort_values('st_optmag').st_optmag
print(st_optmag[st_optmag<3])
pl_hostname
alf Tau 0.85
HD 62509 1.14
Fomalhaut 1.16
gam 1 Leo 1.98
alf Ari 2.00
bet UMi 2.08
Name: st_optmag, dtype: float64
この6つの星は
- アルデバラン
- ポルックス
- フォーマルハウト
- しし座γ星
- おひつじ座α星
- こぐま座β星
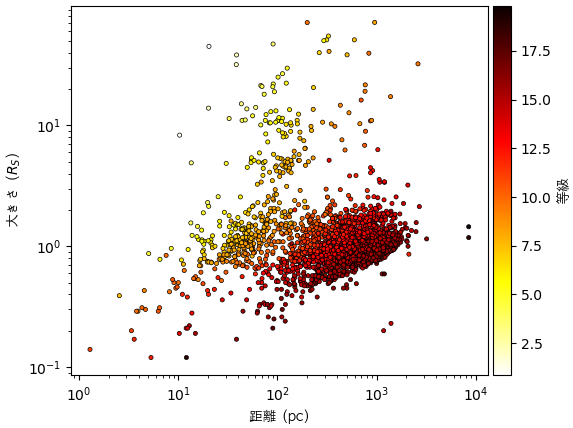
この等級は地球から見る明るさを示すので、星が遠いほど暗く見えます。星の大きさと距離と等級との関係を見ましょう。
df1 = df[(df.st_dist>0)&(df.st_rad>0)&(df.st_optmag>0)].drop_duplicates('pl_hostname')
plt.scatter(df1.st_dist,df1.st_rad,c=df1.st_optmag,marker='.',cmap='hot_r',edgecolor='k',lw=0.5)
plt.xlabel('距離 (pc)',fontname='AppleGothic')
plt.ylabel('大きさ ($R_S$)',fontname='AppleGothic')
cb = plt.colorbar(pad=0.01)
cb.set_label(label='等級',family='AppleGothic')
plt.loglog()
plt.show()
見かけの等級から絶対等級に変換するには
$絶対等級 = 見かけの等級 + 5- 5 \log_{10}{距離}$
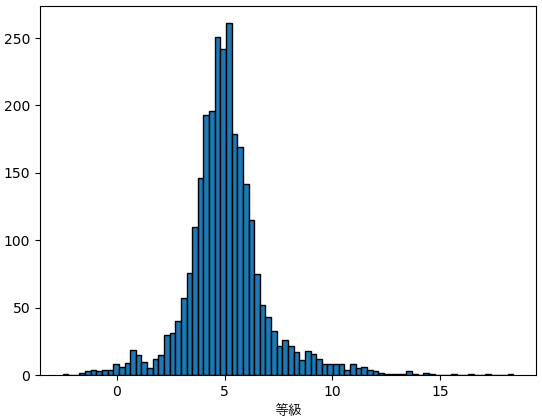
絶対等級を計算して分布を見てみます。
df1 = df[(df.st_optmag>0)&(df.st_dist>0)].drop_duplicates('pl_hostname')
st_mag = df1.st_optmag+5-5*np.log10(df1.st_dist)
print(st_mag.describe())
plt.hist(st_mag,80,ec='k')
plt.xlabel('等級',fontname='AppleGothic')
plt.show()
count 2784.000000
mean 5.077170
std 1.908837
min -2.509848
25% 4.149965
50% 4.958174
75% 5.826980
max 18.386073
dtype: float64
主星の有効温度
主星の有効温度はst_teff列に書いてあります。
df1 = df[df.st_teff>0].drop_duplicates('pl_hostname').sort_values('st_teff',ascending=False)
print(df1.st_teff.describe())
count 2807.000000
mean 5504.664400
std 1442.050143
min 575.000000
25% 5073.000000
50% 5617.000000
75% 5943.000000
max 57000.000000
Name: st_teff, dtype: float64
最も熱いのは57000Kも高い温度ですが、それは数少ないかなり特別なものです。大部分の主星は太陽と同じくらいの5000~6000Kです。
df1 = df[df.st_teff>0].drop_duplicates('pl_hostname').sort_values('st_teff',ascending=False)
print(df1.st_teff.describe())
print(df1.set_index('pl_hostname')[:6][['st_teff','st_optmag','st_rad','st_mass']].replace(0,'-'))
plt.hist(df1.st_teff,100,ec='k')
plt.xlabel('有效溫度 (K)',fontname='AppleGothic')
plt.semilogy()
plt.show()
特に熱い主星の名前を見ておきます。
print(df1.set_index('pl_hostname')[:6][['st_teff','st_optmag','st_rad','st_mass']].replace(0,'-'))
st_teff st_optmag st_rad st_mass
pl_hostname
NN Ser 57000.0 - - 0.54
V0391 Peg 29300.0 14.57 0.23 0.5
KOI-55 27730.0 14.87 0.2 0.5
KIC 10001893 27500.0 15.846 - -
kap And 10900.0 4.14 - 2.6
HIP 78530 10500.0 7.192 - 2.5
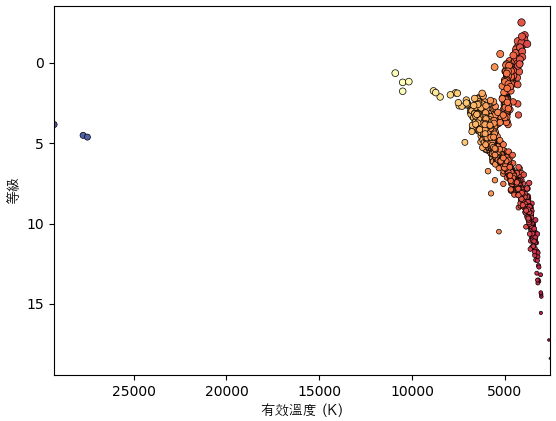
有効温度と絶対等級のグラフを描いたらヘルツシュプルング・ラッセル図になります。
https://ja.wikipedia.org/wiki/ヘルツシュプルング・ラッセル図
df1 = df[(df.st_teff>0)&(df.st_optmag>0)&(df.st_dist>0)].drop_duplicates('pl_hostname')
st_mag = df1.st_optmag+5-5*np.log10(df1.st_dist)
plt.scatter(df1.st_teff,st_mag,(20-st_mag)*5,c=df1.st_teff**0.25,marker='.',cmap='Spectral',edgecolor='k',lw=0.5)
plt.xlabel('有效溫度 (K)',fontname='AppleGothic')
plt.ylabel('等級',fontname='AppleGothic')
plt.xlim(df1.st_teff.max(),df1.st_teff.min())
plt.gca().invert_yaxis()
plt.show()
惑星系の中の惑星の数
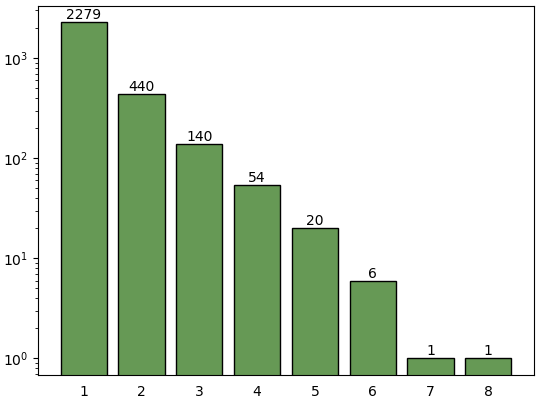
各惑星系の持つ惑星の数はpl_pnum列に書いてあります。一つの惑星系にどれくらいたくさん惑星が見つかったか見てみましょう。
n_pl = np.bincount(df.drop_duplicates('pl_hostname').pl_pnum)[1:]
plt.bar(range(1,len(n_pl)+1),n_pl,color='#669955',ec='k')
for i,n in enumerate(n_pl,1):
plt.text(i,n,'%d'%n,ha='center',va='bottom')
plt.semilogy()
plt.tick_params(bottom=0)
plt.show()
一番惑星の多い惑星系は太陽系と同じく8つです。7つのもあります。
7つと8つの惑星の名前を見ましょう
print(df[df.pl_pnum>=7][['pl_facility','pl_radj','pl_orbper']].sort_index())
pl_facility pl_radj pl_orbper
pl_name
KOI-351 b Kepler 0.117 7.008151
KOI-351 c Kepler 0.106 8.719375
KOI-351 d Kepler 0.256 59.736670
KOI-351 e Kepler 0.237 91.939130
KOI-351 f Kepler 0.257 124.914400
KOI-351 g Kepler 0.723 210.606970
KOI-351 h Kepler 1.008 331.600590
KOI-351 i Kepler 0.118 14.449120
TRAPPIST-1 b La Silla Observatory 0.097 1.510871
TRAPPIST-1 c La Silla Observatory 0.094 2.421823
TRAPPIST-1 d La Silla Observatory 0.069 4.049610
TRAPPIST-1 e Multiple Observatories 0.082 6.099615
TRAPPIST-1 f Multiple Observatories 0.093 9.206690
TRAPPIST-1 g Multiple Observatories 0.101 12.352940
TRAPPIST-1 h Multiple Observatories 0.067 18.767000
惑星を8つ持つ星はKOI-351(別名はKepler-90)です。これらすべての惑星はケプラー宇宙望遠鏡によって発見されたものです。
https://ja.wikipedia.org/wiki/ケプラー90
そして惑星を7つ持つ星はTRAPPIST-1で、ラ・シヤ天文台のTRAPPIST望遠鏡によって発見された惑星系です。
https://ja.wikipedia.org/wiki/TRAPPIST-1
どのような恒星にたくさん惑星が見つけられるか気になるので、5つ以上惑星を持つ主星の性質を見てみましょう。
df1 = df[df.pl_pnum>=5].drop_duplicates('pl_hostname').sort_values('pl_pnum',ascending=False)
df1['st_mag'] = df1.st_optmag+5-5*np.log10(df1.st_dist)
col = ['pl_pnum','st_teff','st_mag','st_rad','st_mass']
print(df1.set_index('pl_hostname')[col].replace(0,'-'))
pl_pnum st_teff st_mag st_rad st_mass
pl_hostname
KOI-351 8 6080.0 4.343527 1.2 1.2
TRAPPIST-1 7 2559.0 18.386073 0.12 0.08
HD 34445 6 5879.0 4.007141 1.38 1.14
Kepler-20 6 5495.0 5.198010 0.96 0.95
HD 219134 6 4699.0 6.488794 0.78 0.81
Kepler-11 6 5663.0 5.262698 1.06 0.96
HD 10180 6 5911.0 4.364564 1.11 1.06
Kepler-80 6 4540.0 7.040659 0.68 0.73
Kepler-102 5 4909.0 6.285037 0.76 0.81
Kepler-84 5 6031.0 4.625214 1.17 -
Kepler-238 5 5751.0 4.401983 1.43 -
Kepler-444 5 5046.0 6.116659 0.75 0.76
Kepler-296 5 3740.0 9.150458 0.48 0.5
Kepler-292 5 5299.0 5.847986 0.83 -
HIP 41378 5 6199.0 3.791010 1.4 1.15
Kepler-122 5 6050.0 4.367544 1.22 -
Kepler-55 5 4503.0 7.019258 0.62 -
Kepler-62 5 4925.0 5.895761 0.64 0.69
GJ 667 C 5 3350.0 11.057455 - 0.33
Kepler-186 5 3755.0 8.447358 0.52 0.54
Kepler-33 5 5904.0 3.755524 1.82 1.29
Kepler-32 5 3900.0 9.044787 0.53 0.58
Kepler-169 5 4997.0 6.006551 0.76 -
55 Cnc 5 5196.0 5.459871 0.94 0.91
Kepler-154 5 5690.0 4.874169 1 -
Kepler-150 5 5560.0 5.149601 0.94 -
HD 40307 5 4956.0 6.610329 - 0.77
K2-138 5 5378.0 5.897745 0.86 0.93
KOI-351(Kepler-90)は太陽と似ている恒星であるのに対し、TRAPPIST-1は暗くて小さい恒星です。
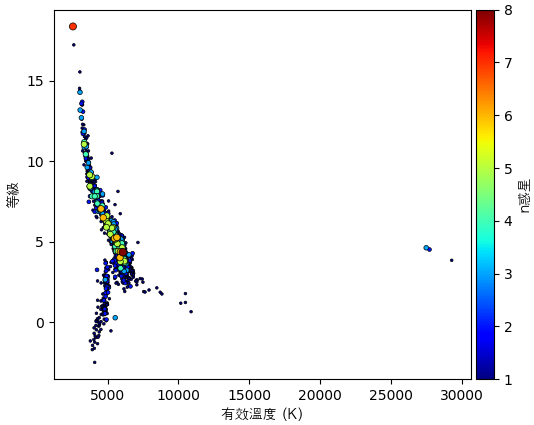
惑星の数と有効温度と絶対等級との関係も見てみます。
df1 = df[(df.st_teff>0)&(df.st_optmag>0)&(df.st_dist>0)].drop_duplicates('pl_hostname').sort_values('pl_pnum')
st_mag = df1.st_optmag+5-5*np.log10(df1.st_dist)
plt.scatter(df1.st_teff,st_mag,df1.pl_pnum*15,c=df1.pl_pnum,marker='.',cmap='jet',edgecolor='k',lw=0.5)
plt.xlabel('有效溫度 (K)',fontname='AppleGothic')
plt.ylabel('等級',fontname='AppleGothic')
cb = plt.colorbar(pad=0.01)
cb.set_label(label='n惑星',family='AppleGothic')
plt.show()
一番上にある茜色の点を示すTRAPPIST-1はその中でかなり目立つな存在です。
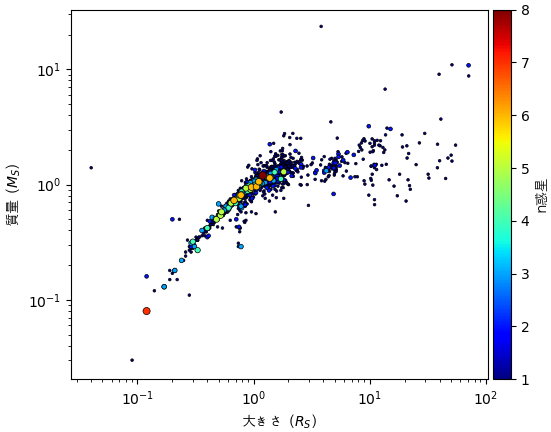
それと、惑星の数と質量と大きさとの関係も。
df1 = df[(df.st_rad>0)&(df.st_mass>0)].drop_duplicates('pl_hostname').sort_values('pl_pnum')
plt.scatter(df1.st_rad,df1.st_mass,df1.pl_pnum*15,c=df1.pl_pnum,marker='.',cmap='jet',edgecolor='k',lw=0.5)
plt.xlabel('大きさ ($R_S$)',fontname='AppleGothic')
plt.ylabel('質量 ($M_S$)',fontname='AppleGothic')
cb = plt.colorbar(pad=0.01)
cb.set_label(label='n惑星',family='AppleGothic')
plt.loglog()
plt.show()
一般的に太陽と似ている恒星には生命が存在する可能性が高いとよく評価されているので、特に注目されています。
纏め
最後にこのデータフレームの中の色んな数値を纏めましょう
f = lambda x: pd.Series({"最小":x[x>0].min(),
"平均":x[x>0].mean(),
"中央値":x[x>0].median(),
"最大":x.max()})
col = ['pl_radj','pl_bmassj','pl_dens','pl_orbincl','pl_orbper','st_dist']
pl = df[col].apply(f).transpose()
pl.index = ['惑星半径 ','惑星質量*','惑星密度 ','軌道傾斜角','軌道周期 ','惑星距離 ']
pl['単位'] = ['木星半径','木星質量','g/cm3','度','日','pc']
col = ['st_rad','st_mass','st_optmag','st_teff','st_dist']
st = df.drop_duplicates('pl_hostname')[col].apply(f).transpose()
st.index = ['主星半径 ','主星質量 ','主星等級 ','主星有効温度 ','主星距離 ']
st['単位'] = ['太陽半径','太陽質量','mag','K','pc']
print(pd.concat([pl,st]))
最小 平均 中央値 最大 単位
惑星半径 0.030000 0.370629 0.208000 6.90 木星半径
惑星質量* 0.000060 2.535104 0.915500 55.59 木星質量
惑星密度 0.030000 2.509603 0.964000 77.70 g/cm3
軌道傾斜角 7.700000 86.100313 88.010000 90.76 度
軌道周期 0.090706 2357.470431 11.989985 7300000.00 日
惑星距離 1.290000 627.859352 492.000000 8500.00 pc
主星半径 0.040000 1.689048 0.990000 71.23 太陽半径
主星質量 0.010000 1.027626 0.980000 23.56 太陽質量
主星等級 0.850000 12.694392 13.659000 20.15 mag
主星有効温度 575.000000 5504.664400 5617.000000 57000.00 K
主星距離 1.290000 658.883689 499.000000 8500.00 pc
*すでに説明したように、惑星の質量は$M sin(i)$になっているものも含まれています。
終わりに
以上、pythonによる系外惑星のデータの纏めでした。系外惑星についてはまだ興味深いことがいっぱいありますが、多すぎる恐れがあるので割愛します。
簡単に天文学のデータを取得できるastroqueryと、大きなデータをこんな簡単に分析できるpandasにとても感謝します。
この記事ではpandasの色んな関数やメソッドを駆使していながらも、全然直接pandasの使い方の説明はしていませんが、pandasを扱う例として使えると思います。
系外惑星の数はどんどん増えていきます。この記事を読んでいる間にも新しい系外惑星が発見され続けているでしょう。