Autodesk MayaではPythonを使ってポリゴンを作る方法は色々ありますね。よくある基本的な形の場合はmaya.cmdsで簡単に作れますが、普段と違う任意な形を作りたい場合、特に数学的な計算に基づく形ならOpenMayaを使うのも良い選択です。
maya.cmdsと比べて、OpenMayaはわかりにくくて冗長なところもあるが、maya.cmdsでは実現できないような細かい作業ができます。
この記事では簡単なポリゴンの作り方をメインとしてOpenMayaの基本的な使い方を説明します。
ここで使うOpenMayaはmaya python API 2.0です。
なお、OpenMayaのバージョンのこととmaya.cmdsやpymelとの違いと速度の比較についてはこの記事で説明してあります。 https://qiita.com/phyblas/items/4b32118498631c1c0e4c
簡単な立方体から
まずは一番簡単な立方体の作り方から例を挙げます。
なお、以下のコードは全部、前もってこのようにインポートしたのは前提となります。以後インポートの記述は省略します。
import maya.cmds as mc
import maya.api.OpenMaya as om
import math
例えば10×10×10サイズの立方体を作りたい場合、maya.cmdsならこう書きますね。
mc.polyCube(w=10,h=10,d=10)
そうしたらこんな立方体が出てきます。

では次は同じようなものをOpenMayaで作ってみましょう。まずコード全体を載せます。詳しい説明は後で。
namae = 'pCube' # トランスフォームのノードの名前
# ポリゴンの頂点
vertices = om.MFloatPointArray([
[-5,-5,-5],
[5,-5,-5],
[5,5,-5],
[-5,5,-5],
[-5,-5,5],
[5,-5,5],
[5,5,5],
[-5,5,5]
])
polygonCounts = [4]*6 # 各面の頂点の数
# 各面はどの番号の頂点を使うか
polygonConnects = [
3,2,1,0,
0,1,5,4,
1,2,6,5,
2,3,7,6,
3,0,4,7,
4,5,6,7
]
trans_fn = om.MFnTransform() # トランスフォームノードを作成
trans_obj = trans_fn.create()
namae = trans_fn.setName(namae) # トランスフォームノードに名前を付ける
fn_mesh = om.MFnMesh() # シェープノードを作成
# 以上の頂点と面の情報を使ってシェープノードの中にポリゴンを作成してトランスフォームのノードにくっつける
fn_mesh.create(vertices,polygonCounts,polygonConnects,parent=trans_obj)
fn_mesh.setName(namae+'Shape') # シェープノードに名前を付ける
maya.cmdsを使う時にはすぐできてしまうので認識していないかもしれませんが、実際にポリゴンを作るのに色んな段階があって複雑ですね。
Mayaのシーンの中に出るポリゴンは少なくとも2つのノードから成されるものです。一つはポリゴン自体の形の情報が入っている「シェープノード」で、もう一つは位置や回転の角度などの情報が入っている「トランスフォームノード」です。
シェープノードはMFnMesh()という関数で作れるものです。作った後、次は.create()メソッドでポリゴンの形を作成します。
その時欲しいポリゴンの情報として3つパラメータが必要です。
-
vertices: 各頂点の位置 -
polygonCounts: 各面に使う頂点の数 -
polygonConnects: 面を作るのに使う頂点番号
立方体は8つの頂点と、6つの四角形の面から成させるものなので、このように書きました。
ただしシェープノードはそのまま単独ではいられなくて、トランスフォームにくっつくのは普通なので、ここでparentというキーワードにトランスフォームノードのオブジェクトを指定する必要があります。
トランスフォームノードはMFnTransform()関数で作れます。そしてシェープノードと同じように.create()を使う必要がありますが、特にパラメータが必要ない。
どのノードでも作られた時に名前が勝手に決められますが、自分で名前を付けたい場合は.setName()メソッドを使います。
maya.cmdsなどによって自動で作られたポリゴンの場合、トランスフォームノードの名前に「Shape」を加えるものをシェープノードの名前として使うのは一般的ですね。
しかしOpenMayaを使う場合、手動でそのような名前を付けるという形になります。
この関数の使い方に関してはもっと詳しくはこれを参考に
MFnMesh: https://help.autodesk.com/view/MAYAUL/2024/JPN/?guid=MAYA_API_REF_py_ref_class_open_maya_1_1_m_fn_mesh_html
MFnTransform: https://help.autodesk.com/view/MAYAUL/2024/JPN/?guid=MAYA_API_REF_py_ref_class_open_maya_1_1_m_fn_transform_html
こんなコードを実行してできたのはこのようなものですが、まだ何かおかしいですね。それはマテリアルがないからです。

普通はどのポリゴンでもマテリアルが必要ですね。maya.cmdsで作ったら自動的に標準のマテリアルであるstandardSurface1が当てられて便利ですが、OpenMayaはそんな機能はないようです。
マテリアルを与えるために、結局maya.cmdsが必要となるでしょう。
mc.select(namae)
mc.hyperShade(a='standardSurface1')
マテリアルを与えたらやっとこのような見慣れた形のポリゴンになりました。

でもまだちょっと様子がおかしい。普通の立方体とは何か違うようですね。
その違和感の正体は「法線の向き」です。
法線を表示させてみたらこのようになります。

普段の立方体なら頂点の法線が面の向きと同じ方向であって、同じ頂点でも違う面における法線は違うはずです。
しかしこの方法で作られたポリゴンの頂点の法線は勝手に決められるからこうなります。
それだけでなく、もう一つ問題があります。uvもまだ定義されていないのです。uvがないので、このままではテクスチャを使うことはできません。
ホリゴンを作る時に頂点と面の情報だけでも一応十分ですが、実は必要に応じて法線とuvの情報も入れられます。
ここはuvと法線の扱いのことも説明します。
uvと法線を定義する方法
以上のコードと同じようなもので、uvと法線の定義も加えたらこう書きます。
namae = 'pCube'
vertices = om.MFloatPointArray([
[-5,-5,-5],
[5,-5,-5],
[5,5,-5],
[-5,5,-5],
[-5,-5,5],
[5,-5,5],
[5,5,5],
[-5,5,5]
])
polygonCounts = [4]*6
polygonConnects = [
3,2,1,0,
0,1,5,4,
1,2,6,5,
2,3,7,6,
3,0,4,7,
4,5,6,7
]
uValues = [0,0,1,1]*6
vValues = [0,1,1,0]*6
normals = [om.MVector(0,0,-1)]*4
normals += [om.MVector(0,-1,0)]*4
normals += [om.MVector(1,0,0)]*4
normals += [om.MVector(0,1,0)]*4
normals += [om.MVector(-1,0,0)]*4
normals += [om.MVector(0,0,1)]*4
faceIds = []
for i in range(6):
faceIds += [i]*4
trans_fn = om.MFnTransform()
trans_obj = trans_fn.create()
namae = trans_fn.setName(namae)
fn_mesh = om.MFnMesh()
fn_mesh.create(vertices,polygonCounts,polygonConnects,uValues,vValues,parent=trans_obj)
fn_mesh.setName(namae+'Shape')
fn_mesh.assignUVs(polygonCounts,polygonConnects)
fn_mesh.setFaceVertexNormals(normals,faceIds,polygonConnects)
mc.select(namae)
mc.hyperShade(a='standardSurface1')
そして実行したらこんな立方体が出てきます。どうやら法線がちゃんと各面に向いています。

ここで各面に法線を定義するのに使うのは.setFaceVertexNormals()というメソッドです。
ちなみに、これは面ごとに法線を決める必要がある場合です。面に関係なく単に各頂点に法線を定義したい場合代わりに.setVertexNormals()を使います。
uvの指定はもう少しややこしいです。まずは.create()を使う時に、uValuesとvValuesという2つパラメータを加える必要があります。
uValuesとvValuesは、テクスチャのuv座標における頂点の位置を示すuとvの値です。
ただしこれだけではuvはまだ与えられていません。次に.assignUVs()というメソッドを使う必要があります。
こうやってuvと法線までコントロールできるということはわかりましたが、実際わざわざそこまでしなくたってポリゴンの形だけ作れれば、後はuvと法線を自動的な方法で与えるだけで十分だという場合が多いでしょう。
例えば多くの場合maya.cmdsのpolySoftEdge()関数で適切に法線を決めることができます。
uvの定義もpolyAutoProjection()という関数などがあります。
polyAutoProjectionとpolySoftEdgeの使い方について詳しくは公式サイトを参考に。
色んな形の作り方
以上、立方体を簡単な例としてポリゴンの作成方法を説明しました。次はもっと複雑な形を作ってみたいと思います。
円錐
立方体のような角ばる形と違って、円錐など曲線があるものを作るのにたくさんポリゴンが必要なので、forループと数学計算が得策となります。
円錐を作るコードはこのように書くことができます。
namae = 'pCone'
h = 4 # 円錐の高さ
r = 3 # 円錐の半径
sx = 24 # 円周の分割
vertices = [[0,h,0]]
polygonConnects = []
for i in range(sx):
theta = 360/sx*i
x = math.sin(math.radians(theta))*r
z = math.cos(math.radians(theta))*r
vertices.append([x,0,z])
polygonConnects += [0,i+1,(i+1)%sx+1]
vertices = om.MFloatPointArray(vertices)
polygonCounts = [3]*sx+[sx]
polygonConnects += list(range(sx,0,-1))
trans_fn = om.MFnTransform()
trans_obj = trans_fn.create()
namae = trans_fn.setName(namae)
fn_mesh = om.MFnMesh()
fn_mesh.create(vertices,polygonCounts,polygonConnects,parent=trans_obj)
fn_mesh.setName(namae+'Shape')
mc.select(namae)
mc.hyperShade(a='standardSurface1')
mc.polySoftEdge(a=30,ch=0)
こうしてこのような普通の円錐ができました。
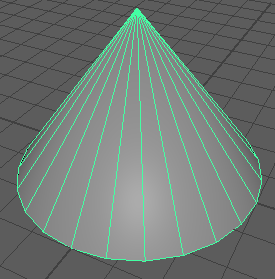
でもただこれだけなら簡単すぎる気もしますね。実際にmaya.cmdsのpolyCone()でもすぐ作れます。
ここではもっと複雑な形を作りましょう。例えば、★みたいな形の円錐を作ります。
namae = 'pStar'
h = 2
r1 = 2
r2 = 3
sx = 100
sw = 5
vertices = [[0,h,0]]
polygonConnects = []
for i in range(sx):
theta = 360/sx*i
r = r1+abs(math.sin(math.radians(theta*sw/2))*(r2-r1))
x = math.sin(math.radians(theta))*r
z = math.cos(math.radians(theta))*r
vertices.append([x,0,z])
polygonConnects += [0,i+1,(i+1)%sx+1]
vertices = om.MFloatPointArray(vertices)
polygonCounts = [3]*sx+[sx]
polygonConnects += list(range(sx,0,-1))
trans_fn = om.MFnTransform()
trans_obj = trans_fn.create()
namae = trans_fn.setName(namae)
fn_mesh = om.MFnMesh()
fn_mesh.create(vertices,polygonCounts,polygonConnects,parent=trans_obj)
fn_mesh.setName(namae+'Shape')
mc.select(namae)
mc.hyperShade(a='standardSurface1')
mc.polySoftEdge(a=30,ch=0)
このような形のポリゴンができます。

もっと弄ったらもっと複雑な形ができますね。
球体
球体は円錐よりも一層複雑なものですが、forループと数学計算でできるのは一緒です。
まずは簡単な球体がこのように書けます。
namae = 'pSphere'
r = 3 # 半径
sx = 36 # 経度の分割
sy = 24 # 緯度の分割
vertices = [[0,r,0]]
polygonConnects = []
for i in range(sx):
polygonConnects += [0,i+1,(i+1)%sx+1]
for j in range(1,sy):
theta = 180/sy*j
for i in range(sx):
phi = 360/sx*i
x = math.sin(math.radians(phi))*math.sin(math.radians(theta))*r
y = math.cos(math.radians(theta))*r
z = math.cos(math.radians(phi))*math.sin(math.radians(theta))*r
vertices.append([x,y,z])
if(j!=sy-1):
polygonConnects += [(i+1)%sx+1+sx*(j-1),i+1+sx*(j-1),i+1+sx*j,(i+1)%sx+1+sx*j]
vertices.append([0,-r,0])
for i in range(sx):
polygonConnects += [(i+1)%sx+sx*(sy-2)+1,i+1+sx*(sy-2),sx*(sy-1)+1]
vertices = om.MFloatPointArray(vertices)
polygonCounts = [3]*sx+[4]*sx*(sy-2)+[3]*sx
trans_fn = om.MFnTransform()
trans_obj = trans_fn.create()
namae = trans_fn.setName(namae)
fn_mesh = om.MFnMesh()
fn_mesh.create(vertices,polygonCounts,polygonConnects,parent=trans_obj)
fn_mesh.setName(namae+'Shape')
mc.select(namae)
mc.hyperShade(a='standardSurface1')
いつも見慣れている球体のポリゴンです。コードちょっと複雑ですが、ちゃんと作れました。

同じような球体はmaya.cmdsのpolySphere()で作れます。
もっと弄って、例えばトカドヘチマ の実みたいな形も作れます。
namae = 'pLuffa'
r1 = 3
r2 = 4
h = 10
sx = 144
sy = 24
sw = 12
vertices = [[0,h/2,0]]
polygonConnects = []
for i in range(sx):
polygonConnects += [0,i+1,(i+1)%sx+1]
for j in range(1,sy):
theta = 180/sy*j
for i in range(sx):
phi = 360/sx*i
r = r1+(math.sin(math.radians(phi*sw/2))*(r2-r1))**2
x = math.sin(math.radians(phi))*math.sin(math.radians(theta))*r
y = math.cos(math.radians(theta))*h/2
z = math.cos(math.radians(phi))*math.sin(math.radians(theta))*r
vertices.append([x,y,z])
if(j!=sy-1):
polygonConnects += [(i+1)%sx+1+sx*(j-1),i+1+sx*(j-1),i+1+sx*j,(i+1)%sx+1+sx*j]
vertices.append([0,-h/2,0])
for i in range(sx):
polygonConnects += [(i+1)%sx+sx*(sy-2)+1,i+1+sx*(sy-2),sx*(sy-1)+1]
vertices = om.MFloatPointArray(vertices)
polygonCounts = [3]*sx+[4]*sx*(sy-2)+[3]*sx
trans_fn = om.MFnTransform()
trans_obj = trans_fn.create()
namae = trans_fn.setName(namae)
fn_mesh = om.MFnMesh()
fn_mesh.create(vertices,polygonCounts,polygonConnects,parent=trans_obj)
fn_mesh.setName(namae+'Shape')
mc.select(namae)
mc.hyperShade(a='standardSurface1')
ドーナツ
次はドーナツ(トーラス)みたいな形を作ります。
namae = 'pDonut'
r = 3 # 輪の半径
sr = 1 # 断面の半径
sx = 36 # 円周での分割
sy = 24 # 断面での分割
vertices = []
polygonConnects = []
for j in range(sx):
theta = 360/sx*j
for i in range(sy):
phi = 360/sy*i
a = math.cos(math.radians(phi))*sr+r
x = a*math.sin(math.radians(theta))
y = math.sin(math.radians(phi))*sr
z = a*math.cos(math.radians(theta))
vertices.append([x,y,z])
polygonConnects += [(i+1)%sy+sy*j,i+sy*j,i+sy*((j+1)%sx),(i+1)%sy+sy*((j+1)%sx)]
vertices = om.MFloatPointArray(vertices)
polygonCounts = [4]*sx*sy
trans_fn = om.MFnTransform()
trans_obj = trans_fn.create()
namae = trans_fn.setName(namae)
fn_mesh = om.MFnMesh()
fn_mesh.create(vertices,polygonCounts,polygonConnects,parent=trans_obj)
fn_mesh.setName(namae+'Shape')
mc.select(namae)
mc.hyperShade(a='standardSurface1')
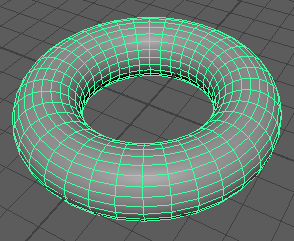
同じようなドーナツはmaya.cmdsのpolyTorus()でも作れます。
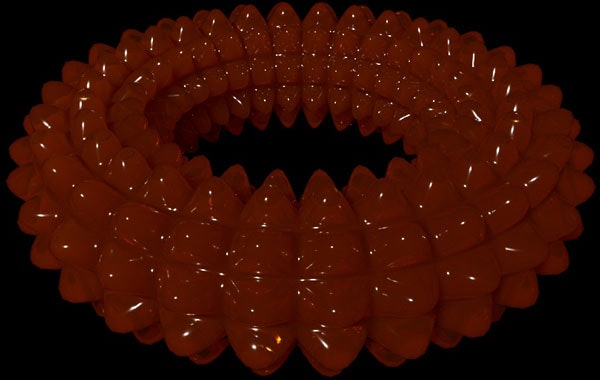
そして最後にナマコみたいに凸凹のあるドーナツも作ってみます。
namae = 'pNamakoDonut'
r = 3
sr1 = 0.8
sr2 = 1.2
sx = 240
sy = 100
swx = 30
swy = 10
vertices = []
polygonConnects = []
for j in range(sx):
theta = 360/sx*j
for i in range(sy):
phi = 360/sy*i
sr = sr1+abs(math.sin(math.radians(theta*swx/2))*math.sin(math.radians(phi*swy/2))*(sr2-sr1))
a = math.cos(math.radians(phi))*sr+r
x = a*math.sin(math.radians(theta))
y = math.sin(math.radians(phi))*sr
z = a*math.cos(math.radians(theta))
vertices.append([x,y,z])
polygonConnects += [(i+1)%sy+sy*j,i+sy*j,i+sy*((j+1)%sx),(i+1)%sy+sy*((j+1)%sx)]
vertices = om.MFloatPointArray(vertices)
polygonCounts = [4]*sx*sy
trans_fn = om.MFnTransform()
trans_obj = trans_fn.create()
namae = trans_fn.setName(namae)
fn_mesh = om.MFnMesh()
fn_mesh.create(vertices,polygonCounts,polygonConnects,parent=trans_obj)
fn_mesh.setName(namae+'Shape')
mc.select(namae)
mc.hyperShade(a='standardSurface1')
でもちゃんとマテリアルを当ててArnoldでレンダリングしたら意外と綺麗に見えますよね。
終わりに
以上、こうやって使いこなせたらOpenMayaで好きな形を色々作れますね。
実際、上述のようにゼロから作らなくたって、maya.cmdsなどで基本的な形を作って、これを元にして色んな形に変形するという方法もありますが、それを実現したい場合もやはりOpenMayaは有効的な方法でしょう。

