LoginSignup
8
12
@phyblas(雛星 φυβλας)

numpyで決定木とランダムフォレストを実装する

Last updated at Posted at 2017-12-02

ここではnumpyで決定木とランダムフォレストを実装するコードを書いてみました。

実装の方法は色んなところから読んだものを参考として自分なりの書き方で纏めたものです。

概念

決定木とランダムフォレストを詳しく説明する記事がもうたくさんあるので、ここでは大雑把しか説明しません。

決定木はあるデータの一つずつの特徴量を考慮してデータを分割していくことで分類問題の答えを探すという機械学習の方法です。

毎回分割する目標は各部分のデータを純粋にすること、つまり『不純度』というものを減らそうとすることです。その不純度はジニ不純度やエントロピーがよく使われます。

毎回不純度を減らせる特徴量を使って分割して、各部分が純粋になるまで分割し続けるので、分割する回数は同じではないことが多い。

このような感じです。

ミクの決定木

分割すればするほど、こんな風に枝が細かく分けられて、小さくなります。

ミクの決定木1
ミクの決定木2
ミクの決定木3
ミクの決定木4
ミクの決定木5

ランダムフォレストは、ブートストラップ法で元のデータセットから何回もランダムで選択されたデータを使ってたくさんの決定木を作ってその決定木によって多数決で答えを出すというものです。木がたくさん集まれば森になると同じように、決定木を集まればランダムフォレストになるとも言えます。一人考えるより、たくさんな人みんな一緒に考えて結果を出す方が効果的ということと同じ。

ミクのランダムフォレスト

クラスの定義

決定木とランダムフォレストのクラスはこのように定義できます

決定木とランダムフォレストのクラス定義
import numpy as np
import matplotlib.pyplot as plt

# ジニ不純度を計算する関数
def gini(p):
    return 1-(p**2).sum()

# ノードのクラス
class Node:
    def __init__(self,X,z,level):
        self.level = level # ノードのレベル
        self.n = len(z) # ノード内のデータの数
        self.eda = [] #このノードから生えた枝
        if(len(np.unique(z))==1): # すでに枝が純粋になった場合
            self.z = z[0]
        elif(level==0): # 設定された最大深さまで分割した場合
            self.z = np.bincount(z).argmax()
        else:
            self.gn = 1 # 最小ジニ不純度の初期化
            # 考慮する特徴量を変えしながら繰り返す
            for j in range(X.shape[1]):
                x = X[:,j]
                xas = x.argsort()
                x_sort = x[xas]
                z_sort = z[xas]
                l = (x_sort[1:]+x_sort[:-1])/2
                l = l[z_sort[1:]!=z_sort[:-1]]
                for ikichi in l:
                    bunki = ikichi>x
                    z_hidari = z[bunki]
                    z_migi = z[~bunki]
                    n_hidari = float(len(z_hidari))
                    n_migi = float(len(z_migi))
                    gn = (gini(np.bincount(z_hidari)/n_hidari)*n_hidari+gini(np.bincount(z_migi)/n_migi)*n_migi)/self.n
                    if(self.gn>gn): # もし新しいジニ不純度がより低ければこの値に変える
                        self.gn = gn
                        self.j = j
                        self.ikichi = ikichi
            o = (self.ikichi>X[:,self.j])
            # 新しいノードを2つ作ってこのノードの枝にする
            self.eda = [Node(X[o],z[o],level-1),Node(X[~o],z[~o],level-1)] 

    def __call__(self,X):
        # もう枝がない場合、答えを出す
        if(self.eda==[]):
            return self.z
        # 枝がある場合、枝のノードに任せる
        else:
            o = self.ikichi>X[:,self.j]
            return np.where(o,self.eda[0](X),self.eda[1](X))

# 決定木のクラス
class Ketteigi:
    def __init__(self,fukasa):
        self.fukasa = fukasa # 分割する最大の数

    def gakushuu(self,X,z):
        self.ne = Node(X,z,self.fukasa) # 根からはじめ、木の中のノードを作る

    def yosoku(self,X): # 予測
        return self.ne(X)

class RandomForest:
    def __init__(self,fukasa,n_ki=10):
        self.fukasa = fukasa
        self.n_ki = n_ki # 決定木の数

    def gakushuu(self,X,z):
        n = len(z) # 入力されたデータの数
        self.k = z.max()+1 # 種類の数
        self.ki = [] # 森の中の全部の決定木を格納するリスト
        for i in range(self.n_ki):
            tt = Ketteigi(self.fukasa)
            s = np.random.choice(n,n) # ブートストラップでランダム
            tt.gakushuu(X[s],z[s]) # ランダムで選択されたデータで学習
            self.ki.append(tt)

    def _yosoku(self,X):
        kekka = 0
        for tt in self.ki:
            kekka += tt.yosoku(X)[:,None]==np.arange(self.k)
        return kekka

    def yosoku(self,X): # 答えを出す
        return self._yosoku(X).argmax(1)

    def yosoku_proba(self,X): # 可能性を出す
        return self._yosoku(X)/self.n_ki

決定木のクラスの中では、たくさんなノードのオブジェクトが作られます。まず根のノードは作らて、根から2本の枝のノードが作られて、その枝からまた2本の枝のノードが作られ、そして繰り返し続けます。

決定木はそのまま使うことも、ランダムフォレストの一部として使うこともできます。

ランダムフォレストを使ったら、その中にたくさんの決定木が作られます。

決定木

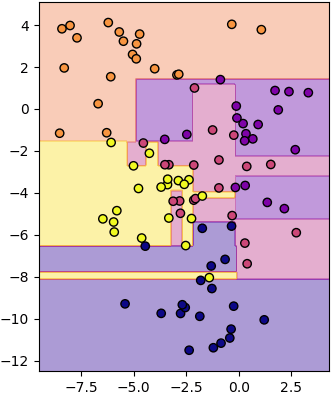
次は実際に使ってみます。まずは決定木。

決定木
from sklearn import datasets
X,z = datasets.make_blobs(n_samples=100,n_features=2,centers=5,cluster_std=1.7,random_state=2)
ketteigi = Ketteigi(100)
ketteigi.gakushuu(X,z)
mx,my = np.meshgrid(np.linspace(X[:,0].min()-1,X[:,0].max()+1,200),np.linspace(X[:,1].min()-1,X[:,1].max()+1,200))
mX = np.stack([mx,my],1)
mz = ketteigi.yosoku(mX)

plt.gca(aspect=1)
plt.scatter(X[:,0],X[:,1],c=z,edgecolor='k',cmap='plasma')
plt.contourf(mx,my,mz,alpha=0.4,cmap='plasma',zorder=0)
plt.show()

決定木

ここで深さは随分高く設定したので、各部分が完全に純粋になるまで分割が続くのですが、そうすれば過学習に陥ることが多いです。深さを低く設定することで分割する回数を制限することができます。

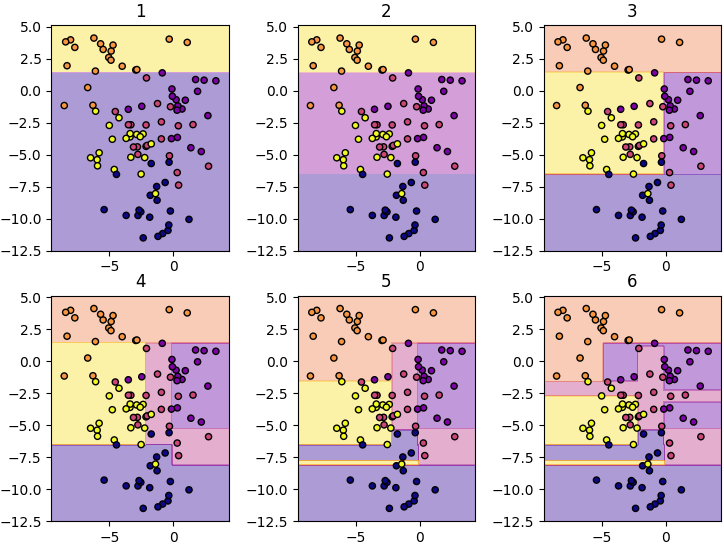
色んな深さで試して比べてみます。

決定木の深さ
mx,my = np.meshgrid(np.linspace(X[:,0].min()-1,X[:,0].max()+1,200),np.linspace(X[:,1].min()-1,X[:,1].max()+1,200))
mX = np.stack([mx,my],1)
plt.figure(figsize=[9,7])
for f in range(1,7):
    ketteigi = Ketteigi(f)
    ketteigi.gakushuu(X,z)
    mz = ketteigi.yosoku(mX)
    plt.subplot(230+f,aspect=1)
    plt.scatter(X[:,0],X[:,1],20,c=z,edgecolor='k',cmap='plasma')
    plt.contourf(mx,my,mz,alpha=0.4,cmap='plasma',zorder=0)
    plt.title('%d'%f)
plt.show()

決定木の深さ

ランダムフォレスト

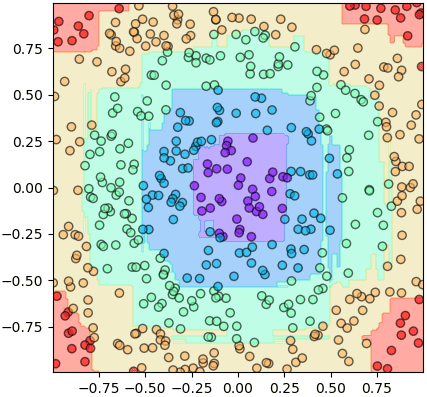
次はランダムフォレストを使ってみます。

ランダムフォレスト
np.random.seed(2)
X = np.random.uniform(-1,1,[500,2])
z = (np.sqrt(X[:,0]**2+X[:,1]**2)//0.282).astype(int)
ranfo = RandomForest(100)
ranfo.gakushuu(X,z)
nmesh = 200
mx,my = np.meshgrid(np.linspace(X[:,0].min(),X[:,0].max(),nmesh),np.linspace(X[:,1].min(),X[:,1].max(),nmesh))
mX = np.stack([mx.ravel(),my.ravel()],1)
mz = ranfo.yosoku(mX).reshape(nmesh,nmesh)
plt.gca(aspect=1,xlim=[mx.min(),mx.max()],ylim=[my.min(),my.max()])
plt.scatter(X[:,0],X[:,1],alpha=0.6,c=z,edgecolor='k',cmap='rainbow')
plt.contourf(mx,my,mz,alpha=0.4,cmap='rainbow',zorder=0)
plt.show()

ランダムフォレスト

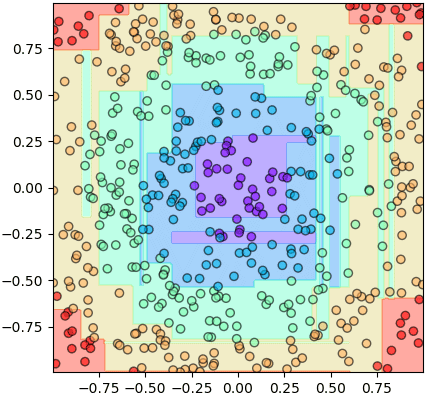
ランダムフォレストの中の決定木を一本取って、予測に使うこともできます。

ランダムフォレストの中の木
mz = ranfo.ki[0].yosoku(mX).reshape(nmesh,nmesh)
plt.gca(aspect=1,xlim=[mx.min(),mx.max()],ylim=[my.min(),my.max()])
plt.scatter(X[:,0],X[:,1],alpha=0.6,c=z,edgecolor='k',cmap='rainbow')
plt.contourf(mx,my,mz,alpha=0.4,cmap='rainbow',zorder=0)
plt.show()

ランダムフォレストの中の木

こうしたことで、一本の決定木よりランダムフォレストの方が細かく分けることがわかります。

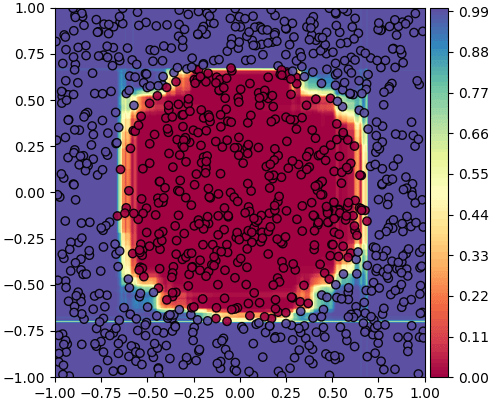
普段ランダムフォレストの中の決定木がそれぞれ違う答えを出して、多数決で一つの答えに纏めるものですが、各答えを選んだ決定木の数から各答えの可能性を予測することもできます。

例えば、100本の決定木を持つランダムフォレストを使って、2つグループに属する可能性を予測してみます

ランダムフォレスト
np.random.seed(11)
X = np.random.uniform(-1,1,[1000,2])
z = (np.sqrt(X[:,0]**2+X[:,1]**2)//0.707).astype(int)
ranfo = RandomForest(100,n_ki=100)
ranfo.gakushuu(X,z)
nmesh = 200
mx,my = np.meshgrid(np.linspace(-1,1,nmesh),np.linspace(-1,1,nmesh))
mX = np.stack([mx.ravel(),my.ravel()],1)
mz = ranfo.yosoku_proba(mX)[:,1].reshape(nmesh,nmesh)
plt.gca(aspect=1,xlim=[mx.min(),mx.max()],ylim=[my.min(),my.max()])
plt.scatter(X[:,0],X[:,1],c=z,alpha=0.9,edgecolor='k',cmap='Spectral')
plt.contourf(mx,my,mz,100,cmap='Spectral',zorder=0)
plt.colorbar(pad=0.01)
plt.show()

可能性分布

終わりに

以上はただ簡単に実装する方法で、実用するにはまだ色々物足りないので、実際に決定木とランダムフォレストを使う時にはやはりsklearnを使った方が効果もよくてもっと色んな機能が使えるはずです。それでも、自分で実装してみることで色々勉強になります。

参考

Python機械学習プログラミング 達人データサイエンティストによる理論と実践 impress top gearシリーズ

使ったmmdモデル

あぴミク http://3xma.blog49.fc2.com/blog-entry-11.html
あぴネル http://www.nicovideo.jp/watch/sm21563089
あぴリン http://www.nicovideo.jp/watch/sm31587977
あぴGUMI http://3xma.blog49.fc2.com/blog-entry-16.html
KAITO http://seiga.nicovideo.jp/seiga/im3101327
YYBレン http://seiga.nicovideo.jp/seiga/im4683139
TDA蒼姫ラピス https://cacti-sloom.deviantart.com/art/Tda-Aoki-Lapis-DL-481846548
桜の道 https://9844.deviantart.com/art/MMD-Cherry-trees-stage-Donwload-643036749
モンスターボール https://phyblas.deviantart.com/art/MMD-DL-pokemon-ball-haifu-682915687

8
12
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
8
12