不均衡画像データのマルチラベル分類

0. はじめに

マルチクラス分類(多クラス分類)とは、一つの画像が複数のクラスの内一つに属する問題です。
一方、一つの画像が複数のクラスに属する、あるいはどのクラスにも属さない問題をマルチラベル分類(多ラベル分類)といいます。
この記事では不均衡データのマルチラベル分類を見ていきます。
使用するのはkeras,tensorflowです。

「4.改善」後の実装はgithubに載せています。Google Colabで動きます。
https://github.com/persimmon-persimmon/mnist-multilabel

google drive直下に以下のようなフォルダ構造を作れば動くと思います。
mnist_multilabl
├data_preparation.ipynb
├train_and_validation.ipynb
├images (data_preparation.ipynbで作成した画像の保存フォルダ)
├model (train_and_validation.ipynbで作成したモデルの保存フォルダ)
└validation (train_and_validation.ipynbで行った検証結果の保存フォルダ)

マルチラベル分類とは

MNISTを例にマルチクラス分類とマルチラベル分類を見てみます。

マルチクラス分類

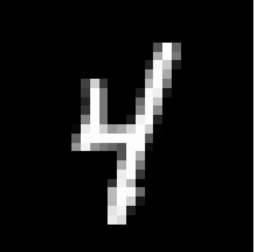
↑の画像は4に属する。

↑の画像は8に属する。
みたいに、マルチクラス分類では一つの画像は必ず一つのクラスに属します。

マルチラベル分類

↑の画像は0,1,2,3,に属する。

↑の画像は4,5に属する。

↑の画像はどのクラスにも属さない。
みたいなのがマルチラベル分類です。

1. データ準備

kerasのMNISTデータセットを元に、↓の感じの画像を作成し保存します。

データまとめ
画像サイズ	224x224
枚数	全部で2万枚(train:val:test=7,2,1)
クラス比率	0,1に分類される画像がもっとも多く、数字が大きくなるほど少なくなる。

以下のコードを実行すると画像とアノテーションcsvが出来上がります。

.py

from keras.datasets import mnist
import numpy as np
import pandas as pd
import cv2
from sklearn.model_selection import train_test_split
import random
from PIL import Image
(_x_train_val, _y_train_val), (_x_test, _y_test)=mnist.load_data()
_x_train, _x_val, _y_train, _y_val = train_test_split(_x_train_val, _y_train_val, test_size=0.2)
train = {i:[x for x, t in zip(_x_train, _y_train) if t == i] for i in range(10)}
val = {i:[x for x, t in zip(_x_val, _y_val) if t == i] for i in range(10)}
test = {i:[x for x, t in zip(_x_test, _y_test) if t == i] for i in range(10)}
image_set = {"train":train,"val":val,"test":test}

n_image = {"train":14000,"val":4000,"test":2000} # 画像枚数
random.seed(0)
height = 224 # 画像サイズ
width = 224
weight = [30,30,25,25,20,20,15,15,10,10] # 各クラスの発生確率
ary = []
for data_type in ["train","val","test"]:
    for t in range(1,n_image[data_type]+1):
        blank = np.zeros((height, width, 3)) # 真っ黒画像を用意
        label=[0] * 10
        for i in range(10):
            if random.random()<weight[i]/100:# クラスごとに画像に入れるかを判断する
                im = random.choice(image_set[data_type][i]) # ランダムに画像をチョイス
                x_ = int(random.uniform(0,height-28)) # ランダムに描画位置を決める
                y_ = int(random.uniform(0,width-28))
                blank[x_:x_+28,y_:y_+28,0] += im
                blank[x_:x_+28,y_:y_+28,1] += im
                blank[x_:x_+28,y_:y_+28,2] += im
                label[i]=1
        filepath = f'images/{data_type}_{str(t).zfill(6)}.jpg'
        ary.append([filepath,data_type]+label)
        cv2.imwrite(filepath,blank)
df = pd.DataFrame(ary)
df.columns=["filepath","data_type"]+[str(i) for i in range(10)]
df.to_csv("data.csv",index=False)

↓アノテーションcsv

data.csv

filepath,data_type,0,1,2,3,4,5,6,7,8,9
images/train_000001.jpg,train,0,0,0,0,0,0,0,0,0,0
images/train_000002.jpg,train,0,0,0,0,0,0,0,0,0,0
images/train_000003.jpg,train,0,0,0,0,0,1,0,0,0,0
images/train_000004.jpg,train,1,0,0,0,0,0,0,0,0,0
images/train_000005.jpg,train,1,1,0,0,0,1,0,0,0,0
images/train_000006.jpg,train,0,0,0,0,0,0,0,0,0,0
images/train_000007.jpg,train,0,1,0,0,0,0,0,0,0,0

2. 学習

不均衡データ、マルチラベル分類のためのポイントがあります。
・不均衡データなので、損失関数を工夫する。
・マルチラベル分類なので、CNNの出力層の活性化関数をsigmoidにする。
・不均衡データ向け、マルチラベル分類向けの評価関数を作る。
それぞれ以下で記述します。

損失関数

不均衡データの学習でも、マルチクラス分類なら少ないクラスの画像をデータ拡張で増やすか、多いクラスの画像を減らすかすればいいですが、一枚の画像が複数のクラスに分類するマルチラベル分類では難しいです。
そこで損失関数を工夫します。
各クラスにたいして、バッチ内のposi,negaの比率の逆数を損失に掛けます。
posi:クラスに属する。
nega:クラスに属さない。

.py

def binary_crossentropy_balance(target, output):
    beta_p = batch_size / (K.epsilon() + K.sum(target,axis=0))
    beta_n = batch_size / (K.epsilon() + batch_size - K.sum(target,axis=0))
    epsilon_ = constant_op.constant(K.epsilon(), output.dtype.base_dtype)
    output = clip_ops.clip_by_value(output, epsilon_, 1. - epsilon_)
    bce = target * math_ops.log(output + K.epsilon()) * beta_p 
    bce += (1 - target) * math_ops.log(1 - output + K.epsilon()) * beta_n
    return -K.sum(bce, axis=-1)

モデル

モデルはVGG16->GAP->Dense(512)->Dense(n_class)のシンプルなものです。
VGG16の転移学習で、出力層の活性化関数をsigmoidにしています。
出力層の活性化関数をsigmoidにすれば他はなんでもいいです。

.py

def get_multilabel_model(n_class,n_trainable_layer=1,input_shape=(224,224,3))->Model:
    """
    マルチラベル分類用のモデルを返す.
    VGG16->GAP->Dense(512)->Dense(n_class)
    :param n_class:予測クラス数
    :param n_trainable_layer:出力層から何層目までを学習可能層にするか
    :param input shape:入力サイズ
    """
    input = Input(input_shape)
    vgg16 = VGG16(include_top=False, weights='imagenet', input_tensor=input)
    x = vgg16.output
    x = GlobalAveragePooling2D()(x)
    x = Dense(512,kernel_regularizer=regularizers.l2(0.05), activation='relu')(x)
    output = Dense(n_class,kernel_regularizer=regularizers.l2(0.05), activation='sigmoid')(x)
    model = Model(inputs=input,outputs=output)
    # non-trainable layers 重みを固定
    for layer in model.layers:
        layer.trainable = False
    for layer in model.layers[-n_trainable_layer:]:
        layer.trainable = True
    return model

評価関数

マルチラベル分類向けの評価関数としてtotal_acc,binary_acc(参考の「1つの画像が複数のクラスに属する場合（Multi-label）の画像分類」をご参照ください)、
不均衡データ向けの評価関数としてrecall,precisionを作成しました。
たとえばクラス9は全体の10%しか登場しないため、すべてnega(クラスに属さない)予測すれば正解率が90%になります。これは良くないので、recall,precisionを使います。
presicion:モデルがposiと予測して真の値がposiの割合
recall:真の値がposiのもののうち、モデルがposiと予測した割合

.py

# total_acc,binary_accは参考の「1つの画像が複数のクラスに属する場合（Multi-label）の画像分類」を参照
def total_acc(y_true, y_pred):
    pred = K.cast(K.greater_equal(y_pred, 0.5), "float")
    flag = K.cast(K.equal(y_true, pred), "float")
    return K.prod(flag, axis=-1)

def binary_acc(y_true, y_pred):
    pred = K.cast(K.greater_equal(y_pred, 0.5), "float")
    flag = K.cast(K.equal(y_true, pred), "float")
    return K.mean(flag, axis=-1)

# モデルがposiと予測して真の値がposiの割合
def precision(y_true, y_pred):
    true_positives = K.sum(K.cast(K.greater(K.clip(y_true * y_pred, 0, 1), 0.5), 'float32'))
    pred_positives = K.sum(K.cast(K.greater(K.clip(y_pred, 0, 1), 0.5), 'float32'))
    precision = true_positives / (pred_positives + K.epsilon())
    return precision

# 真の値がposiのもののうち、モデルがposiと予測した割合
def recall(y_true, y_pred):
    true_positives = K.sum(K.cast(K.greater(K.clip(y_true * y_pred, 0, 1), 0.5), 'float32'))
    poss_positives = K.sum(K.cast(K.greater(K.clip(y_true, 0, 1), 0.5), 'float32'))
    recall = true_positives / (poss_positives + K.epsilon())
    return recall

全体の実装

.py

import os
import csv
import random
import csv
import numpy as np
import pandas as pd
from PIL import Image
import tensorflow as tf
from tensorflow.keras.utils import Sequence
from tensorflow.keras import backend as K
from tensorflow.keras import regularizers
from tensorflow.keras.applications.vgg16 import VGG16
from tensorflow.keras.layers import Input,Dense,GlobalAveragePooling2D,Activation,Conv2D,BatchNormalization,AveragePooling2D,Flatten,Add
from tensorflow.keras.models import Model
from tensorflow.keras.callbacks import History,LearningRateScheduler,ModelCheckpoint,EarlyStopping
from tensorflow.keras.optimizers import Adam,SGD
from sklearn.metrics import confusion_matrix,roc_curve,auc,roc_auc_score,recall_score,precision_score,accuracy_score,f1_score
from tensorflow.python.framework import constant_op
from tensorflow.python.ops import clip_ops,math_ops
import matplotlib.pyplot as plt


def get_multilabel_model(n_class,n_trainable_layer=1,input_shape=(224,224,3))->Model:
    """
    マルチラベル分類用のモデルを返す.
    VGG16->GAP->Dense(512)->Dense(n_class)
    :param n_class:予測クラス数
    :param n_trainable_layer:出力層から何層目までを学習可能層にするか
    :param input shape:入力サイズ
    """
    input = Input(input_shape)
    vgg16 = VGG16(include_top=False, weights='imagenet', input_tensor=input)
    x = vgg16.output
    x = GlobalAveragePooling2D()(x)
    x = Dense(512,kernel_regularizer=regularizers.l2(0.05), activation='relu')(x)
    output = Dense(n_class,kernel_regularizer=regularizers.l2(0.05), activation='sigmoid')(x)
    model = Model(inputs=input,outputs=output)
    # non-trainable layers
    for layer in model.layers:
        layer.trainable = False
    for layer in model.layers[-n_trainable_layer:]:
        layer.trainable = True
    return model

# 学習のためのデータgenerator
class MyMnistDataSequence(Sequence):
    def __init__(self,records,batch_size,input_shape):
        """
        :params records:[[filepath,データ区分(TRAIN,VAL,TEST),ラベル0~9],[,,],[..],..]
        :params batch_size:バッチサイズ.一度の__getitem__で返すデータ件数.
        :params input_size:入力画像サイズ.画像をこのサイズに変換する.
        """
        self.records = records
        self.batch_size = batch_size
        self.input_shape = input_shape

    def __getitem__(self, idx):
        batch_records=self.records[idx * self.batch_size:(idx + 1) * self.batch_size]
        data = list(map(self.x_y_from_record,batch_records))
        x=[]
        y=[]
        for xi,yi in data:
            x.append(xi)
            y.append(yi)
        return  np.array(x,dtype=np.float32),np.array(y,dtype=np.float32)

    def getitem_with_filepath(self, idx):
        batch_records=self.records[idx * self.batch_size:(idx + 1) * self.batch_size]
        data = list(map(self.x_y_from_record,batch_records))
        x=[]
        y=[]
        for xi,yi in data:
            x.append(xi)
            y.append(yi)
        return  np.array(x,dtype=np.float32),np.array(y,dtype=np.float32),np.array([x[0] for x in batch_records])

    def __len__(self):
        return int(np.ceil(len(self.records) / float(self.batch_size)))

    def on_epoch_end(self):
        random.shuffle(self.records)

    def x_y_from_record(self,record):
        img_file=record[0]
        with Image.open(img_file) as f:
            img = f.convert('RGB').resize((self.input_shape[0],self.input_shape[1]))
        x = np.asarray(img, dtype=np.float32) / 255
        label=record[-10:]
        return x,np.array(label,dtype=np.int32)

# 評価関数定義
# total_acc,binary_accは参考の「1つの画像が複数のクラスに属する場合（Multi-label）の画像分類」を参照
def total_acc(y_true, y_pred):
    pred = K.cast(K.greater_equal(y_pred, 0.5), "float")
    flag = K.cast(K.equal(y_true, pred), "float")
    return K.prod(flag, axis=-1)

def binary_acc(y_true, y_pred):
    pred = K.cast(K.greater_equal(y_pred, 0.5), "float")
    flag = K.cast(K.equal(y_true, pred), "float")
    return K.mean(flag, axis=-1)

# モデルがposiと予測して真の値がposiの割合
def precision(y_true, y_pred):
    true_positives = K.sum(K.cast(K.greater(K.clip(y_true * y_pred, 0, 1), 0.5), 'float32'))
    pred_positives = K.sum(K.cast(K.greater(K.clip(y_pred, 0, 1), 0.5), 'float32'))
    precision = true_positives / (pred_positives + K.epsilon())
    return precision

# 真の値がposiのもののうち、モデルがposiと予測した割合
def recall(y_true, y_pred):
    true_positives = K.sum(K.cast(K.greater(K.clip(y_true * y_pred, 0, 1), 0.5), 'float32'))
    poss_positives = K.sum(K.cast(K.greater(K.clip(y_true, 0, 1), 0.5), 'float32'))
    recall = true_positives / (poss_positives + K.epsilon())
    return recall

# データ準備
with open("data.csv") as f:
    ldr=csv.reader(f)
    record=[x for x in ldr]
train_record=[x for x in record if x[1]=="train"]
val_record=[x for x in record if x[1]=="val"]
test_record=[x for x in record if x[1]=="test"]

batch_size=64
input_shape=(224,224,3)

# Loss Function
def binary_crossentropy_balance(target, output):
    beta_p = batch_size / (K.epsilon() + K.sum(target,axis=0))
    beta_n = batch_size / (K.epsilon() + batch_size - K.sum(target,axis=0))
    epsilon_ = constant_op.constant(K.epsilon(), output.dtype.base_dtype)
    output = clip_ops.clip_by_value(output, epsilon_, 1. - epsilon_)
    bce = target * math_ops.log(output + K.epsilon()) * beta_p 
    bce += (1 - target) * math_ops.log(1 - output + K.epsilon()) * beta_n
    return -K.sum(bce, axis=-1)

model=get_multilabel_model(n_class=10,input_shape=input_shape)
model_checkpoint = ModelCheckpoint(
    filepath=os.path.join("model", 'weight.h5'),
    save_best_only=True,monitor='val_loss',mode='min',verbose=1)
Ecall=EarlyStopping(monitor='val_loss',patience=5,restore_best_weights=False)
model.compile(Adam(epsilon=K.epsilon()), loss=binary_crossentropy_balance,metrics=[total_acc,binary_acc,recall,precision])

n_epoch=50
vb_index=1
initial_epoch=0
model.fit(
    x=MyMnistDataSequence(train_record,batch_size,input_shape),
    steps_per_epoch=len(train_record)//batch_size,
    epochs=n_epoch,
    initial_epoch=initial_epoch,
    validation_data=MyMnistDataSequence(val_record,batch_size,input_shape),
    validation_steps=len(val_record)//batch_size,
    callbacks=[model_checkpoint,Ecall],
    workers=4,
    use_multiprocessing=False,
    verbose=vb_index
)

実行すると、10epochぐらいでEarlyStoppingがかかり止まります。

3. 評価

valデータセットで評価した結果です。reacllなどの閾値は0.5。やはり出現頻度の多い0,1クラスの分類は精度が高めです。

target	roc_auc	recall	precision	accuracy
0	0.81741	0.80684	0.49899	0.69225
1	0.76199	0.76121	0.43429	0.63675
2	0.73211	0.78542	0.36401	0.6025
3	0.77122	0.78834	0.40640	0.649
4	0.70858	0.80180	0.27713	0.55525
5	0.75065	0.77398	0.31960	0.629
6	0.71515	0.63414	0.24495	0.667
7	0.73054	0.72857	0.25571	0.62325
8	0.73401	0.47457	0.21166	0.76325
9	0.71864	0.51371	0.19656	0.74075

ROC曲線

各クラスのROC曲線およびAUCです。

ROC曲線は真陽性率と偽陽性率の関係をプロットしたものです。縦が真陽性率で横が偽陽性率です。
真陽性率：真の値が1の画像の内、正しく1と予測された割合。高いほどいい。高いほど取りこぼし少ない。
偽陽性率：真の値は0の画像の内、間違って1と予測される割合。低いほどいい。
どれだけの偽陽性率を許容すれば、どの程度の真陽性率を達成できるかを表しています。
99%以上がクラス0でクラス1は1%未満のときなど、データの偏りがひどい場合、偽陽性率が低くてもprecisionがめちゃくちゃ悪くなったりします。そういうケースではPR曲線(precision-recall曲線)およびPR曲線で計算したAUCを使うといいみたいです。
ROC曲線とPR曲線の違いは以下の記事がわかりやすいです。

予測値の分布

各クラスの予測値の分布です。
青が真の値がnegaの画像に対するモデルの予測値の分布で、オレンジがposi画像に対するモデルの予測値の分布です。

4. 改善[追記]

上の実装ではgeneratorを自作しましたが、ふつうにImageDataGeneratorを使ったほうがいいです。これでVGG16の前処理とデータ拡張します。

VGG16用前処理

ImageDataGeneratorの引数でpreprocessing_function=tf.keras.applications.vgg16.preprocess_inputとします。
転移学習に使った学習済みVGG16用の前処理がかかります。

Data Argumentation

ImageDataGeneratorの引数でrotation_range=10,~~などを指定します。

学習時のgeneratorに、ImageDataGenerator.flow_from_dataframeを使います。マルチラベル分類なのでclass_mode="raw"とし、ラベルカラムをy_col=label_colで指定します。

.py

def get_data_generator():
  """
  data_generatorを返す
  """
  # 画像前処理にVGG16の前処理とデータ拡張
  datagen = ImageDataGenerator(
      preprocessing_function=tf.keras.applications.vgg16.preprocess_input,
      rotation_range=10,
      zoom_range=0.1,
      width_shift_range=0.1,
      height_shift_range=0.1
      )
  return datagen
datagen=get_data_generator()
# ラベルカラム
label_col=[str(i) for i in range(10)]
# generator用DataFrameのカラム
cols=["filepath","data_type"]+label_col

# train用generator
df_train=pd.DataFrame(train_record,dtype=np.uint8)
df_train.columns=cols
df_train[label_col]=df_train[label_col].astype(np.float32)
gen_train=datagen.flow_from_dataframe(df_train,directory="",x_col="filepath",y_col=label_col,target_size=(224,224),color_mode='rgb',class_mode="raw",batch_size=batch_size)

# validation用generator
df_val=pd.DataFrame(val_record)
df_val.columns=cols
df_val[label_col]=df_val[label_col].astype(np.float32)
gen_val=datagen.flow_from_dataframe(df_val,directory="",x_col="filepath",y_col=label_col,target_size=(224,224),color_mode='rgb',class_mode="raw",batch_size=batch_size)

Test Time Argumentation (TTA)

学習時に行ったデータ拡張を予測時にも使います。一枚の画像から生成した複数の画像に対し予測を行い、その平均値を最終的な予測値とします。

tta.py

# test用generator
test_batch_size=100
df_test=pd.DataFrame(test_record)
df_test.columns=cols
df_test[label_col]=df_test[label_col].astype(np.float32)
datagen=get_data_generator(data_arg=tta)
gen_test=datagen.flow_from_dataframe(df_test,directory="",x_col="filepath",y_col=label_col,target_size=(224,224),color_mode='rgb',class_mode="raw",batch_size=test_batch_size)
tta_epoch=30
y_pred=np.zeros((len(df_val),10),dtype=np.float32)
y_true=np.zeros((len(df_val),10),dtype=np.float32)
steps=len(df_test)//test_batch_size
for _ in range(tta_epoch):
  for i in range(steps):
    x,y=gen_test.next()
    y_pred[i*test_batch_size:(i+1)*test_batch_size]+=model.predict(x)
    y_true[i*test_batch_size:(i+1)*test_batch_size]=y
y_pred /= tta_epoch # 予測の平均を取る

全体の実装はgithubを参照ください。

改善結果

改善結果のROC曲線とPR曲線と予測値の分布を載せます。
図の描画のコードもgithubにあります。

VGG16前処理

平均ROC-AUC:0.94999

VGG16前処理 + データ拡張

平均ROC-AUC:0.945929

VGG16前処理 + データ拡張 + TTA

平均ROC-AUC:0.806139

VGG16の前処理を入れるだけで大きく改善しました。今回、データ拡張は効果なく、TTAでは精度が悪化しました。
TTAについて、可視化した図から推測するに、何かしら数字のある画像にはそれがどんな数字であれすべてのクラスをposiと予測しているっぽいです。
実際、TTA予測値のクラス間の相関係数の平均を計算すると0.98385でした。つまり、どれかのクラスをposiと予測したら他のクラスもほとんどposiと予測していることになります。
ちなみにTTAなしだと0.747113です。

参考

マルチラベル分類の参考記事

損失関数設計の参考論文
https://arxiv.org/pdf/1705.02315.pdf

TTAの参考記事