LoginSignup
0
0
@perico_v1

数理最適化と単体法(simplex method)の備忘録

Posted at

背景・目的

実務で最適化問題を扱っていたことがあるのですが、求解部分はソルバー任せだったので、アルゴリズム部分の理解を深めたくて勉強しました。その内容を自分用のメモとしてまとめておきます。

数理最適化問題について

数理最適化問題は、ある制約条件の元で目的関数を最大化(最小化)する変数(決定変数)の値を求める問題。
目的関数、制約条件、変数の性質で分類され、大きく連続最適化問題・離散最適化問題に分けられ、その中でも制約条件などの性質で細分化される。代表的な分類は以下の通り。

  • 連続最適化問題: 変数が連続的な値をとる問題
    • 線形計画問題: 目的関数および制約条件が線形となる問題
    • 非線形計画問題: 目的関数や制約条件に非線形関数を含む問題
  • 離散最適化問題(組み合わせ最適化問題): 変数が離散的な値をとる問題
    • 整数計画問題: 変数が整数値のみをとる問題。有名な問題としてナップサック問題や巡回セールスマン問題がある
      • 0-1整数計画問題: 変数が{0, 1}の2値のみをとる問題
    • 混合整数計画問題: 連続値をとる変数と整数値をとる変数がともに存在する問題

目的関数を最大化(最小化)する変数の値を最適解と呼び、その時の目的関数の値を最適値と呼ぶ。最適化問題には常に最適解が存在するわけではなく、解いた結果として大きく以下の4つに分けられる。

  • 実行不能(infeasible): 制約条件を満たす変数が存在しない場合
  • 非有界(unbounded): 目的関数の値が無限に大きく(小さく)改善できる場合
  • 有界だが最適解なし: 目的関数の値が有限であるが解が存在しない場合
    • 例えば目的関数が$\frac{1}{x}$のように漸近的に0に近づく性質の際に、最小化する場合など
  • 最適解あり: 制約条件を満たす変数の中で目的関数を最大化(最小化)する解が存在する場合

線形計画問題について

線形計画問題(linear programming problem; LP)について詳しく見てみる。
線形計画問題とは、以下2点を満たす最適化問題のこと。
① 目的関数が線形関数
② 制約条件が全て線形の等式もしくは不等式

例えば、次のような問題。

\begin{align}
最大化\quad 5x_{1}+8x_{2} \\
条件 \qquad x_{1}\geq 0 \\
x_{2}\geq 0 \\
x_{1}+2x_{2}\leq 10 \quad・・・①\\
3x_{1}+4x_{2}\leq 24　\quad・・・②\\
2x_{1}+x_{2}\leq 14　\quad・・・③
\end{align}

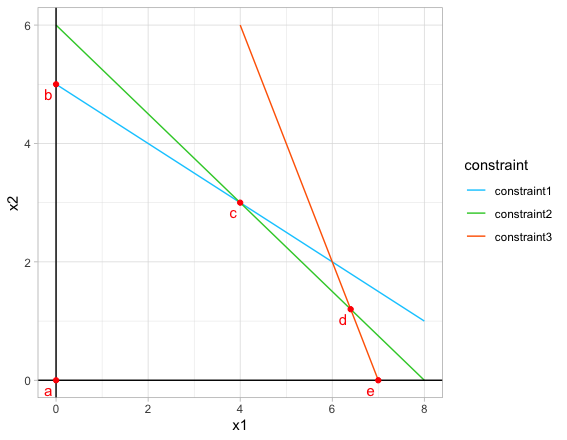
この問題をx1,x2平面上で表すと以下のグラフになる。
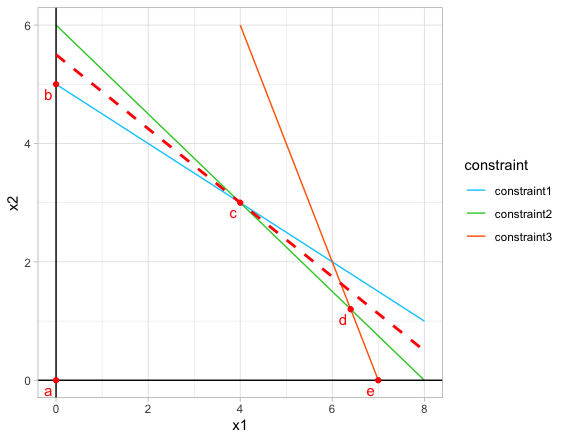
Rplot.png
青・緑・オレンジの直線がそれぞれ制約条件①②③を表しており、実行可能領域は①②③の直線とx1x2軸で囲まれた五角形の部分になる。赤の点線は目的関数を表し、目的関数のとる値は切片で表されている。高校数学では目的関数の直線をスライドさせて、切片が最大となる場合を探すことで問題を解いていたと思う。この問題では、目的関数が$点c(4,3)$を通るときに最大となる。

図の作成に使ったコードは以下(※Rで作成。Pythonでも良かったのですが、たまにはRを使おうと思った次第です)。

library(dplyr)
library(ggplot2)

# 制約条件 ------------------------------------------------------------
x1 <- seq(0, 10, by=1)
x2 <- -0.5*x1 + 5 # 制約条件1
dat <- data.frame(x1=x1, x2.1=x2)

x2 <- -0.75*x1 + 6 #制約条件2
dat <- dat %>% dplyr::mutate(x2.2=x2)

x2 <- -2*x1 + 14 #制約条件3
dat <- dat %>% dplyr::mutate(x2.3=x2)

head(dat)
# x1 x2.1 x2.2 x2.3
# 1  0  5.0 6.00   14
# 2  1  4.5 5.25   12
# 3  2  4.0 4.50   10
# 4  3  3.5 3.75    8
# 5  4  3.0 3.00    6
# 6  5  2.5 2.25    4

# tidyなデータに整形 -------------------------------------------------------------
dat2 <- dat %>% 
  tidyr::gather(key=key, value=x2, x2.1:x2.3, factor_key=FALSE) %>% 
  dplyr::mutate(
    # ラベル名をグラフ用に書き換え
    constraint = case_when(
      key=="x2.1" ~ "constraint1",
      key=="x2.2" ~ "constraint2",
      key=="x2.3" ~ "constraint3",
      TRUE ~ "others"
    )
  ) %>% 
  dplyr::select(-key)

head(dat2)
# x1  x2  constraint
# 1  0 5.0 constraint1
# 2  1 4.5 constraint1
# 3  2 4.0 constraint1
# 4  3 3.5 constraint1
# 5  4 3.0 constraint1
# 6  5 2.5 constraint1

# 交点のラベルを作成
dat3 <- data.frame(
  x1=c(0, 0, 4, 6.4, 7), 
  x2=c(0, 5, 3, 1.2, 0), 
  lab=c("a", "b", "c", "d", "e"), 
  constraint="(not constraint)"
)

# 目的関数の直線を作成
x1 <- seq(0, 10, by=1)
x2 <- -5/8*x1 + 5.5 # 目的関数が最大値を取る場合の直線
dat4 <- data.frame(x1=x1, x2=x2, constraint="(not constraint)")

# グラフ描画 -------------------------------------------------------------------
# カラーパレットの色
cbPalette <- c("#00CCFF", "#33CC33", "#FF6600")

ggplot(data=dat2, aes(x=x1, y=x2, group=constraint, colour=constraint)) + 
  scale_colour_manual(values=cbPalette) + # カラーパレットをマニュアルで指定
  geom_line() + 
  geom_hline(aes(yintercept=0)) + # x2=0
  geom_vline(aes(xintercept=0)) + # x1=0
  xlim(0, 8) +
  ylim(0, 6) +
  geom_point(data=dat3, aes(x=x1, y=x2), colour="red", size=1.5) + # 頂点
  geom_text(data=dat3, aes(x=x1, y=x2, label=lab, hjust=1.4, vjust=1.4), colour="red", size=4) + # 頂点のデータラベル
  geom_line(data=dat4, aes(x=x1, y=x2), colour="red", linetype="dashed", size=1) + # 目的関数の直線
  theme_light()

標準形(standard form)について

すべての線形計画問題は、目的関数・変数・制約条件が以下の条件を満たした標準形になおすことができる。

  • 目的関数: 最大化
  • 変数: すべての変数に非負制約が付く
  • 制約条件: 非負制約を除くすべての制約条件で「左辺の値 $\leq$ 右辺の値」
\begin{align}
最大化\quad \sum_{j=1}^{n}c_{j}x_{j} \\
条件\qquad \sum_{j=1}^{n}a_{ij}x_{j} &\leq b_{i}, \quad i=1,...,m, \\
x_{j} &\geq 0, \quad j=1,...,n.
\end{align}

任意の線形計画問題を標準形になおすために行う操作は以下3つ。

  • 目的関数について
    • もとの問題が目的関数の最小化だった場合→目的関数を-1倍する
  • 変数について
    • 非負制約のない変数$x_{j}$があった場合→非負制約のついた変数$x_{j}^{+}, x_{j}^{-}$を新たに置き、$x_{j}=x_{j}^{+}-x_{j}^{-}$と置き換える
  • 制約条件について
    • 等式の制約条件$a_{ij}x_{j}=b_{i}$は2つの不等式の制約条件$a_{ij}x_{j}\geq b_{i},\quad a_{ij}x_{j}\leq b_{i}$に変える
    • 「左辺の値 $\geq$ 右辺の値」 となる制約条件を-1倍して「左辺の値 $\leq$ 右辺の値」になおす

単体法(simplex method)について

  • 線形計画問題を現実的な処理時間で解く効率的なアルゴリズムの1つ
  • 1947年にアメリカの数学者ジョージ・ダンツィクによって提案された
  • 制約条件を満たす解を1つ求め、そこから目的関数を改善する解を効率的に探索し、最適解を求める手法

単体法のアルゴリズムの概要

  1. 制約条件に非負制約のついた変数であるスラック変数を導入する
  2. スラック変数を用いて、辞書と呼ばれる形式に変換する
  3. 実行可能な解を1つ求める
  4. 他の変数を固定した上で変数を1つ増加(減少)させ、目的関数の値を改善する解を求める(ピボット操作)
  5. 辞書を更新する
  6. 4, 5を繰り返し、目的関数の改善ができなくなった段階で終了する

単体法を実践してみる(手計算)

線形計画問題についてで挙げた以下の問題を例に、単体法で手計算してみる。

\begin{align}
最大化\quad 5x_{1}+8x_{2} \\
条件 \qquad x_{1}\geq 0 \\
x_{2}\geq 0 \\
x_{1}+2x_{2}\leq 10 \quad・・・①\\
3x_{1}+4x_{2}\leq 24　\quad・・・②\\
2x_{1}+x_{2}\leq 14　\quad・・・③
\end{align}

Rplot01.png

STEP1: スラック変数を導入する

まずはじめに、線形計画問題の非負制約以外の制約条件①②③に対し、非負制約のついた変数(スラック変数)を導入して等式で表す。

\begin{align}
x_{1}+2x_{2}+x_{3} &= 10 \\
3x_{1}+4x_{2}+x_{4} &= 24　\\
2x_{1}+x_{2}+x_{5} &= 14　\\
x_{3}\geq 0, \, x_{4}\geq 0, &\, x_{5}\geq 0
\end{align}

STEP2: 辞書で表す

STEP1の式を式変形し、スラック変数を左辺に持ってくると最適化問題は以下の通りに表せる。

\begin{align}
最大化\quad z&=5x_{1}+8x_{2} \\
条件 \quad
x_{3} &= 10 - x_{1} -2x_{2} \quad・・・④\\
x_{4} &= 24 - 3x_{1} - 4x_{2}　\quad・・・⑤\\
x_{5} &= 14 - 2x_{1} - x_{2}　\quad・・・⑥\\
x_{1}, &\, x_{2}, \, x_{3}, \, x_{4}, \, x_{5} \geq 0 \\
\end{align}

上記の式から、単体法に必要な部分を取り出したものが以下式であり、これを辞書と呼ぶ。

\begin{align}
最大化\quad z&=5x_{1}+8x_{2} \\
条件 \quad
x_{3} &= 10 - x_{1} -2x_{2} \\
x_{4} &= 24 - 3x_{1} - 4x_{2}　\\
x_{5} &= 14 - 2x_{1} - x_{2}　\\
\end{align}

STEP3:実行可能な解を1つ求める

STEP2の条件式の右辺の変数$x_1, x_2=0$と固定すると、$x_3=10,　x_4=24,　x_5=14$ となり、実行可能解が1つ求まる。これは$x_1,x_2$平面のグラフ上では点a(原点)である。

なお、0に固定された$x_1,x_2$は非基底変数、それ以外の$x_3,　x_4,　x_5$は基底変数と呼ばれる。基底変数、非基底変数含め、単体法における解についての言葉の定義を整理すると以下の通り。

  • 基底解: n次元空間内の頂点。例題では$a,b,c,d,e$などの点
  • 実行可能基底解: 基底解のうち、実行可能な解のこと
  • 基底変数: 基底解のうち、0に固定されなかった変数。STEP3では$x_3, x_4, x_5$
  • 非基底変数: 基底解を定める際に値を0に固定した変数。STEP3では$x_1, x_2$

STEP4:他の変数を固定した上で変数を1つ増加(減少)させ、目的関数の値を改善する解を求める(ピボット操作)

目的関数$z=5x_1+8x_2$より、$x_1$より$x_2$の係数のほうが大きいので、$x_2$の値を大きくするほうが目的関数の値を改善できる。そこで、$x_1=0$に固定したまま$x_2$の値を大きくしてみる。
STEP2の辞書に$x_1=0$を代入すると

\begin{align}
最大化\quad z&=8x_{2} \\
条件 \quad
x_{3} &= 10 -2x_{2} \\
x_{4} &= 24 - 4x_{2}　\\
x_{5} &= 14 - x_{2}　\\
\end{align}

ここで$x_3, x_4, x_5 \geq 0$ より、$x_2$のとりうる最大値は$x_2=5$である。このとき上の条件式より、$x_3=0, x_4=4, x_5=9$と求まる。これは$x_1,x_2$平面のグラフ上では点eである。
この操作は基底変数と非既定変数を入れ替える操作であり、ピボット操作と呼ばれる。

STEP5:辞書を更新する

基底変数と非基底変数を入れ替えたので、それに合わせて辞書を更新する。具体的には、基底変数($x_2, x_4, x_5$)を非基底変数($x_1, x_3$)で表すように元々の辞書から式変形を行う。

STEP2の④式を変形して、$x_2=5- \frac{1}{2}x_1 - \frac{1}{2}x_3$
これを目的関数$z=5x_{1}+8x_{2}$と⑤式⑥式にそれぞれ代入して、新しい辞書が得られる。

\begin{align}
最大化\quad z &= 40 + x_1 - 4x_3 \\
条件 \quad
x_2 &= 5- \frac{1}{2}x_1 - \frac{1}{2}x_3 \\
x_4 &= 4 - x_1 + 2x_3　\\
x_5 &= 9 - \frac{3}{2}x_1 + \frac{1}{2}x_3　\\
\end{align}

STEP6:目的関数が改善しなくなるまでピボット操作と辞書更新を繰り返す

ピボット操作

STEP5で求めた辞書の目的関数を見ると、$x_3$の係数はマイナスなので、目的関数の値を改善するには$x_1$の値を大きくする必要がある。$x_3=0$に固定しつつ、$x_1$の値を大きくすると

\begin{align}
最大化\quad z &= 40 + x_1 \\
条件 \quad
x_2 &= 5- \frac{1}{2}x_1 \\
x_4 &= 4 - x_1 \\
x_5 &= 9 - \frac{3}{2}x_1 \\
\end{align}

ここで$x_2, x_4, x_5 \geq 0$ より、$x_1$のとりうる最大値は$x_1=4$である。このとき上の条件式より、$x_2=3, x_4=0, x_5=3$と求まる。これは$x_1,x_2$平面のグラフ上では点c$(4, 3)$である。

辞書の更新

まず、$x_1$を$x_3,x_4$で表す。
1つ前の辞書の$x_4 = 4 - x_1 + 2x_3$を変形して、$x_1 = 4 + 2x_3 - x_4$
この式を1つ前の辞書の目的関数、条件式それぞれに代入して新しい辞書が得られる。

\begin{align}
最大化\quad z &= 44 - 2x_3 - x_4 \\
条件 \quad
x_1 &= 4 + 2x_3 - x_4 \\
x_2 &= 3 - \frac{3}{2}x_3 + \frac{1}{2}x_4　\\
x_5 &= 3 - \frac{5}{2}x_3 + \frac{3}{2}x_4　\\
\end{align}

ここで、目的関数$z = 44 - 2x_3 - x_4$は$x_3, x_4$のどちらも係数が負でありどちらの変数を増加させても改善の余地がない。よってこの時点での解が最適解である。

以上より、最適解は$(x_1, x_2) = (0, 3)$であり、最適値は$z = 44$

単体法を実践してみる(python, pulpを用いた検算)

手計算で求めた解が合っているかの検算のため、pythonでも同じ問題を解いてみる。

import pulp

# 問題の定義
# name: 問題の名前を記載。問題を.lpファイルに出力した際にこの名前で書き出される。
# sense: LpMinimize(最小化)かLpMaximize(最大化)を指定。デフォルトではLpMinimize。
problem = pulp.LpProblem(name='SampleLinearProblem', sense = pulp.LpMaximize)

# 変数の定義
# name: 変数の名前。問題を.lpファイルに出力した際に使われる
# lowBound: 変数の下限。デフォルトでは負の無限大
# cat: 変数の分類。Integer, Binary, Continuousのいずれかを指定。デフォルトではContinuous
x1 = pulp.LpVariable(name='X1', lowBound=0, cat='Continuous')
x2 = pulp.LpVariable(name='X2', lowBound=0, cat='Continuous')

# 目的関数
problem += 5 * x1 + 8 * x2

# 制約条件
problem += x1 + 2 * x2 <= 10
problem += 3 * x1 + 4 * x2 <= 24
problem += 2 * x1 + x2 <= 14

# 問題をlpファイルに書き出す
# 目的関数、制約条件、変数が書き出される
problem.writeLP('SampleLinearProblem.lp')

# 制約条件式の一覧を表示する
for name, value in problem.constraints.items():
    print(name, ': ', value)
# _C1 :  X1 + 2*X2 <= 10
# _C2 :  3*X1 + 4*X2 <= 24
# _C3 :  2*X1 + X2 <= 14

# 求解
status = problem.solve()
print(pulp.LpStatus[status])
# Optimal

# 求解後の変数の値を表示
for v in problem.variables():
    print(v.name, "=", v.varValue)
# X1 = 4.0
# X2 = 3.0

# 求解後の変数の値を表示(変数を指定して取り出す場合)
# print('x1:', x1.value())
# print('x2:', x2.value())

# 最適値の表示
pulp.value(problem.objective)
# 44.0

pulpで解いた結果も最適解が$(x_1, x_2)=(4, 3)$、最適値が$44$となり、手計算の結果と一致。

単体法を実践してみる(行列表記)

単体法を手短に説明している書籍では数式でなく行列で表記されていることがよくある。行列表記に慣れるために、先程計算した問題を行列でも記載しておく。なお、最適解に到達するまでではなく、一度目のピボット操作までを記載する。

まず、標準形の線形計画問題にスラック変数を導入して等式に変形した線形計画問題(STEP1: スラック変数を導入するに記載の問題)を行列を使って以下のように表記する。

\begin{align}
最大化\quad 
\textbf{c}^{\top }\textbf{x} &= 

\begin{pmatrix}
5&8&0&0&0
\end{pmatrix} 

\begin{pmatrix}
x^{1} \\
x^{2} \\
x^{3} \\
x^{4} \\
x^{5} \\
\end{pmatrix} \\

条件 \quad
\textbf{A}\textbf{x} &= \textbf{b}, \quad \textbf{x} \geq \textbf 0 \\
\\
条件式の行列の中身は \quad
&\begin{pmatrix}
1 & 2 & 1 & 0 & 0 \\
3 & 4 & 0 & 1 & 0 \\
2 & 1 & 0 & 0 & 1 \\
\end{pmatrix}

\begin{pmatrix}
x^{1} \\
x^{2} \\
x^{3} \\
x^{4} \\
x^{5} \\
\end{pmatrix} 

=

\begin{pmatrix}
10 \\
24 \\
14 \\
\end{pmatrix}

\end{align}

ここで、以下の変数を導入する。

  • $\textbf{x}_\textbf{N}$: 非基底変数を表す行列
  • $\textbf{x}_\textbf{B}$: 基底変数を表す行列
  • $\textbf{N}$: 制約条件の係数行列$\textbf{A}$のうち非基底変数の係数の部分行列
  • $\textbf{B}$: 制約条件の係数行列$\textbf{A}$のうち基底変数の係数の部分行列

先程の手計算の最初の実行可能基底解ではそれぞれの変数の内容は以下である。

\begin{align}
\textbf{x}_\textbf{N} = 
\begin{pmatrix}
x^{1} \\
x^{2} \\
\end{pmatrix} 

&, \quad

\textbf{x}_\textbf{B} = 
\begin{pmatrix}
x^{3} \\
x^{4} \\
x^{5} \\
\end{pmatrix} \\

\\

\textbf{N} = 
\begin{pmatrix}
1&2 \\
3&4 \\
2&1 \\
\end{pmatrix}

&, \quad

\textbf{B} = 
\begin{pmatrix}
1&0&0 \\
0&1&0 \\
0&0&1 \\
\end{pmatrix}
\end{align}

すると、$\textbf{A} \textbf{x}$は次のように表せる。

\begin{align}
\textbf{A} \textbf{x} &= 
\begin{pmatrix}
1&2&1&0&0 \\
3&4&0&1&0 \\
2&1&0&0&1 \\
\end{pmatrix} 

\begin{pmatrix}
x^{1} \\
x^{2} \\
x^{3} \\
x^{4} \\
x^{5}
\end{pmatrix} \\

&=

\begin{pmatrix}
1&2 \\
3&4 \\
2&1 \\
\end{pmatrix}

\begin{pmatrix}
x^{1} \\
x^{2} \\
\end{pmatrix} 

+

\begin{pmatrix}
1&0&0 \\
0&1&0 \\
0&0&1 \\
\end{pmatrix}

\begin{pmatrix}
x^{3} \\
x^{4} \\
x^{5} \\
\end{pmatrix} \\

&= \textbf{N} \textbf{x}_\textbf{N} + \textbf{B} \textbf{x}_\textbf{B} \\

\\
\\

よって \qquad \textbf{N} \textbf{x}_\textbf{N} &+ \textbf{B} \textbf{x}_\textbf{B} = \textbf{b} \quad・・・⑦

\end{align}

また、目的関数$\textbf{z} = \textbf{c}^{\top }\textbf{x}$について以下変数を導入する。

  • $\textbf{c}_\textbf{N}$: 非基底変数の係数行列
  • $\textbf{c}_\textbf{B}$: 基底変数の係数行列
    先程の手計算の最初の実行可能基底解ではそれぞれの変数の内容は以下である。
\begin{align}

\textbf{c}_\textbf{N} = 
\begin{pmatrix}
5 \\
8 \\
\end{pmatrix} 

, \quad

\textbf{c}_\textbf{B} = 
\begin{pmatrix}
0 \\
0 \\
0
\end{pmatrix} 

\end{align}

すると、$\textbf{c}^{\top }\textbf{x}$は次のように表せる。

\begin{align}

\textbf{c}^{\top }\textbf{x} &= 

\begin{pmatrix}
5&8&0&0&0
\end{pmatrix} 

\begin{pmatrix}
x^{1} \\
x^{2} \\
x^{3} \\
x^{4} \\
x^{5} \\
\end{pmatrix} \\

&= 

\begin{pmatrix}
5&8
\end{pmatrix} 

\begin{pmatrix}
x^{1} \\
x^{2} \\
\end{pmatrix}

+

\begin{pmatrix}
0&0&0
\end{pmatrix}

\begin{pmatrix}
x^{3} \\
x^{4} \\
x^{5} \\
\end{pmatrix} \\

&= 

\textbf{c}^{\top }_\textbf{N} \textbf{x}_\textbf{N} +
\textbf{c}^{\top }_\textbf{B} \textbf{x}_\textbf{B}

\\
\\

よって \qquad \textbf{z} &= 
\textbf{c}^{\top }_\textbf{N} \textbf{x}_\textbf{N} +
\textbf{c}^{\top }_\textbf{B} \textbf{x}_\textbf{B} \quad・・・⑧

\end{align}

式$⑦$の両辺に左から$\textbf{B}^{-1}$をかけると

\begin{align}
\textbf{B}^{-1} \textbf{N} \textbf{x}_ \textbf{N} + \textbf{x}_ \textbf{B} = \textbf{B}^{-1} \textbf{b} &
\\
\\
\textbf{x}_ \textbf{B} = \textbf{B}^{-1} \textbf{b} - \textbf{B}^{-1} \textbf{N} \textbf{x}_ \textbf{N} & \quad・・・⑨
\end{align}

これを式$⑧$に代入すると

\begin{align}
\textbf{z} &= 
\textbf{c}^{\top }_\textbf{N} \textbf{x}_\textbf{N} +
\textbf{c}^{\top }_\textbf{B} \textbf{x}_\textbf{B}
\\ 
&= 
\textbf{c}^{\top }_\textbf{N} \textbf{x}_\textbf{N} + 
\textbf{c}^{\top }_\textbf{B} ( \textbf{B}^{-1} \textbf{b} - \textbf{B}^{-1} \textbf{N} \textbf{x}_ \textbf{N} )
\\
&=
\textbf{c}^{\top }_\textbf{B} \textbf{B}^{-1} \textbf{b} + (\textbf{c}^{\top }_\textbf{N} - \textbf{c}^{\top }_\textbf{B} \textbf{B}^{-1} \textbf{N}) \textbf{x}_\textbf{N}\quad・・・⑩
\end{align}

ここで、

\textbf{x}_ \textbf{N} = 
\begin{pmatrix}
x^{1} \\
x^{2} \\
\end{pmatrix}
=
\begin{pmatrix}
0 \\
0 \\
\end{pmatrix}

と固定すると、式$⑨$より

\textbf{x}_ \textbf{B} = 
\begin{pmatrix}
x^{3} \\
x^{4} \\
x^{5} \\
\end{pmatrix}
= \textbf{B}^{-1} \textbf{b}
=
\begin{pmatrix}
1&0&0 \\
0&1&0 \\
0&0&1 \\
\end{pmatrix}
\begin{pmatrix}
10 \\
24 \\
14 \\
\end{pmatrix}
=
\begin{pmatrix}
10 \\
24 \\
14 \\
\end{pmatrix}

となり、$\textbf{x}_ \textbf{B}$の値が求まる。今回は$\textbf{x}_ \textbf{B} \geq 0$なので、実行可能基底解である。

また、

  • $\textbf{b}'　=　\textbf{B}^{-1}　\textbf{b}$
  • $\textbf{c}'_　\textbf{N} = \textbf{c}^{\top }_　\textbf{N}　-　\textbf{c}^{\top }_\textbf{B}　\textbf{B}^{-1}　\textbf{N}$
  • $\textbf{N}' = \textbf{B} ^{-1} \textbf{N}$

とおくと、式⑨⑩より

  • $\textbf{z} = \textbf{c}^{ \top } _\textbf{B} \textbf{b}' + \textbf{c}' _\textbf{N} \textbf{x} _\textbf{N}$
  • $\textbf{x} _\textbf{B} = \textbf{b}' - \textbf{N}' \textbf{x} _ \textbf{N}$

$\textbf{c}' _\textbf{N}$は非基底変数の係数ベクトルであり、被約費用と呼ばれる。$\textbf{c}' _ \textbf{N}$の各要素は対応する非基底変数の値を1増加させた時の目的関数の値の改善量を表す。

ここで$\textbf{c}'_ \textbf{N}$の各要素を${c'} _{i}$とし、対応する非基底変数を${x} _{i}$とおく。
このとき、目的関数の係数が正となる非基底変数が存在する、すなわち${c'} _{k} > 0$となる${c'} _{k}, {x} _{k}$が存在する場合はこの${x} _{k}$を増加することで目的関数の値が改善する。今回は${x} _{1}, {x} _{2}$のいずれを増加させても目的関数が改善できるが、動かせる変数は1つであるので係数の大きい${x} _{2}$を増加させる。1

他の非基底変数(${x} _{1}$)の値を0に保ちながら${x} _{2}$の値を増加する。$\textbf{a} _{2}$を非基底変数${x} _{2}$に対応する$\textbf{N}'$の列とすると、$\textbf{a}^{\top } _{2} =
\begin{pmatrix}
2 \
4 \
1 \
\end{pmatrix}
$である。

${x} _{2}$の値を${x} _{2} = \theta$まで増加させた際の目的関数と基底変数の値はそれぞれ

\begin{align}
\textbf{z} &= \textbf{c} ^{\top } _\textbf{B} \textbf{b}' + {c}' _{2} \theta \\
 &= 
\begin{pmatrix}
0&0&0 \\
\end{pmatrix}

\begin{pmatrix}
1&0&0 \\
0&1&0 \\
0&0&1 \\
\end{pmatrix}

\begin{pmatrix}
10 \\
24 \\
14 \\
\end{pmatrix} + 8 \theta \\
 &= 8 \theta \\
\\
\textbf{x} _\textbf{B} &= \textbf{b}' - \theta \textbf{a} _{2} \\
 &= 
\begin{pmatrix}
1&0&0 \\
0&1&0 \\
0&0&1 \\
\end{pmatrix}
\begin{pmatrix}
10 \\
24 \\
14 \\
\end{pmatrix}
- \theta
\begin{pmatrix}
2 \\
4 \\
1 \\
\end{pmatrix} \\
 &= 
\begin{pmatrix}
10 \\
24 \\
14 \\
\end{pmatrix}
- \theta
\begin{pmatrix}
2 \\
4 \\
1 \\
\end{pmatrix} \\
 &=
\begin{pmatrix}
10 - 2 \theta \\
24 - 4 \theta \\
14 - 4 \theta \\
\end{pmatrix}
 
\end{align}

ここで、$\textbf{x}_ \textbf{B} \geq 0$より、$\textbf{b}', \textbf{a}_ {2}$の各要素をそれぞれ${b'}_ {i}, {a}_ {i2}$とすると、

\theta = min \left\{ \frac{b'_i}{{a}_{i2}} \right\}

であり、今回は$\theta = 5$となる。
$x_2$を5まで増加させると同時に、$x_3 = 0$となり、基底変数と非基底変数が入れ替わる(ピボット操作)。入れ替わった基底変数と非基底変数をもとに辞書を更新し、被約費用$\textbf{c}'_ {N}$を計算して再びピボット操作を行う。この手順を繰り返して、目的関数が改善しなくなった時点($\textbf{c}'_ {N} \leq 0$となった時点)で終了する。

最適解を求めることが難しい場合の対処方法

手計算の説明に使った例題では、初めに作った辞書で実行可能基底解が得られたが、必ずしもそうなる問題ばかりではない。また、最適解を求めることが困難な問題も多い。そうした場合の対処方法の中に、2段階単体法、双対問題、緩和問題といったものがある。これらについて簡単に記載しておく。

  • 2段階単体法
    • 実行可能基底解がすぐに得られない場合に、単体法の前に1段階手順を設ける
    • 元の問題を解く前に、実行可能基底解を求める補助問題を作成しそれを解くことで元の問題の実行可能基底解、辞書を得る
    • 補助問題を解いた後の手順は単体法と同じ
  • 双対問題
    • 最適解を直接求めることが困難な場合に、元の問題(主問題と呼ぶ)の代わりに解く問題であり、最適値の上界(下界)を求めることを目的とした問題
    • 主問題が最大化であれば、双対問題は最適値の上界を求める問題であり、主問題が最小化であれば、双対問題は最適値の下界を求める問題
    • 良い上界(下界)を求めることで、実行可能解の目的関数の値が最適値かどうか判断することができるようになる
    • 制約条件の1次結合を用いて作られる
  • 緩和問題
    • 双対問題と同じく、最適化問題の最適解を直接求めることが困難な場合に、最適値の上界(下界)を求めることを目的とした問題
    • 主問題が「$最大化: \ f( \textbf x) \quad 条件: \ \textbf x \in S $」であるとき、$\overline f( \textbf x) \geq f( \textbf x) ~ ( \textbf x \in S ), ~ \overline S \supseteq S $を満たす$\overline f( \textbf x), \overline S$を用いて 「$最大化: \ \overline f( \textbf x) \quad 条件: \ \textbf x \in \overline S $」と表される

終わりに

教科書によっては単体法の説明が行列表記のみでサラッと済まされているもあるのですが、参考文献のしっかり学ぶ数理最適化にはかなり親切に記載されており、大変ありがたかったです。こちらの本は私ですと読むのにかなり時間がかかるので、また暇を見て読み進められたらなと思います。

参考文献

  1. $c'_k > 0$という条件だけでは増加させる変数$x_k$は唯一つには決まらない。この時の変数の選択基準は複数あるが、今回は最大係数規則と呼ばれる、被約費用$c'_k$の値が最大となる$x_k$を選ぶ方法をとっている。 ↩

0
0
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
0
0