はじめに
レーザー分岐させたくないですか?
僕はさせたいです。
そんなあなたに誰でもできるレーザーの分岐方法について伝授します
対象読者
レーザーを購入したはいいが、一本のレーザーだけでは加工が大変だと感じているあなた
※ちなみにこちらのHAMAMATSU PHOTONICSさんの動画を見ると、今からやろうとしていることのイメージがつきやすいと思います
https://www.youtube.com/watch?v=BhLONC7LOJ0
前提条件・知識
簡単に書きます。多少厳密さに欠ける点はお許しを。
あなたはレーザーを分岐させようとしています。
レーザーは光です。光は波です。波なので振幅と位相を持ちます。
光学レンズはフーリエ変換作用を持っています。要はレンズを通った光はフーリエ変換された状態になると思ってください。
(興味のある方はこちらなどが分かりやすいです:https://hoshistar81.jp/pdf/111111doc.pdf)。
あなたは元々のレーザーの振幅は分かっています。
また、レンズ透過後にレーザーがどんな振幅になっていて欲しいかは既に決まっています。
原理
いま、あなたは何らかの位相の状態でレーザーをぶっ放し、それがレンズを通ったら目的の形になっていていることを願っています。
しかし、レーザーをどんな位相にすれば、レンズを通った後に目的の形(振幅)になっているのかがわかりません。
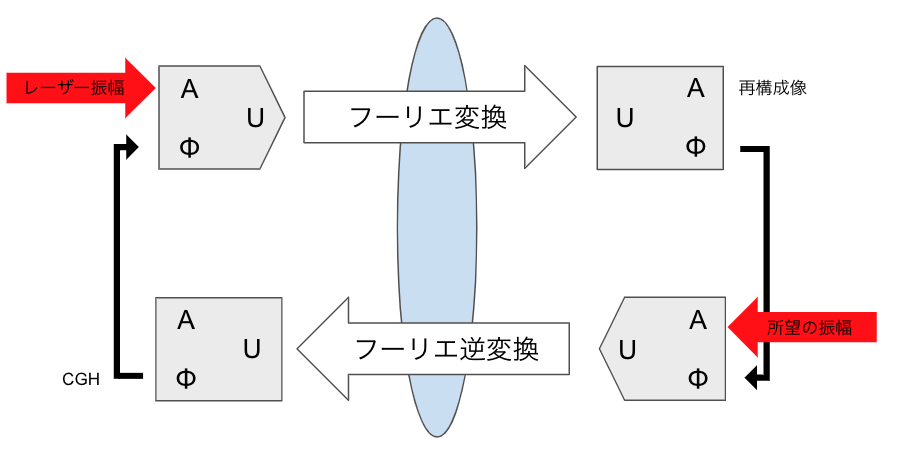
この 「どんな位相であればいいか」 を知る方法に 反復フーリエ変換法 というものがあります。
今あなたが持つ情報は
- レンズを通る前のレーザーの振幅
- レンズを通った後のレーザーの振幅(自分の目的の形)
- レンズを通ることはフーリエ変換と等価であるという事実
です。
いま、レンズを通る前をa、レンズを通った後をbとします。
するとaからみたbはフーリエ変換後であり、bからみたaは逆フーリエ変換後であると言えます。
a領域での振幅を元々のレーザーの振幅にセット。位相は何かランダムな値でセット(最初だけ)。
それをフーリエ変換(aからbへレンズ透過)。
b領域での振幅を目的の振幅にセット。位相は渡ってきた値そのままでセット。
それをフーリエ逆変換(bからaへレンズ透過)。
a領域での振幅を元々のレーザーの振幅にセット。位相は渡ってきた値そのままでセット。
これをひたすら繰り返し行います。すると、フーリエ変換前と後の振幅に合わせて、位相がよしなに最適化されていきます。
これがフーリエ反復法です。名前に恥じぬ通り、ひたすらフーリエ変換と逆変換を繰り返すだけの単純な手法ですね。
実装
これをPythonで実装すると以下のコードの様になります。
import cv2
import numpy as np
import matplotlib.pyplot as plt
def check_uniformity(u_int, target):
u_int = u_int / np.max(u_int)
maxi = np.max(u_int[target==1])
mini = np.min(u_int[target==1])
uniformity = 1 - (maxi-mini)/(maxi+mini)
print("均一性:", uniformity)
return uniformity
def normalization(origin):
maxi = np.max(origin)
mini = np.min(origin)
norm = ((origin - mini) / (maxi - mini))
return norm
def hologram(phase):
phase = np.where(phase<0, phase+2*np.pi, phase)
p_max = np.max(phase)
p_min = np.min(phase)
holo = ((phase - p_min)/(p_max- p_min)) * 255
holo = holo.astype("uint8")
return holo
def reconstruct(norm_int):
rec = norm_int * 255
rec = rec.astype("uint8")
return rec
def main():
target = cv2.imread("img/target.bmp",0)
cv2.imshow("target",target)
cv2.waitKey(0)
height, width = target.shape[:2]
target = target / 255
laser = 1
phase = np.random.rand(height, width)
u = np.empty_like(target, dtype="complex")
iteration = 20
uniformity = []
for num in range(iteration):
u.real = laser * np.cos(phase)
u.imag = laser * np.sin(phase)
#-------レンズ---------
u = np.fft.fft2(u)
u = np.fft.fftshift(u)
#-------レンズ---------
u_abs = np.abs(u)
u_int = u_abs ** 2
norm_int = normalization(u_int)
uniformity.append(check_uniformity(u_int,target))
phase = np.angle(u)
u.real = target * np.cos(phase)
u.imag = target * np.sin(phase)
#-----レンズ---------
u = np.fft.ifftshift(u)
u = np.fft.ifft2(u)
#-------レンズ---------
phase = np.angle(u)
holo_name = "holo"
rec_name = "rec"
holo = hologram(phase)
cv2.imwrite("img/{}.bmp".format(holo_name), holo)
cv2.imshow("Hologram", holo)
cv2.waitKey(0)
rec = reconstruct(norm_int)
cv2.imwrite("img/{}.bmp".format(rec_name), rec)
cv2.imshow("Reconstruction", rec)
cv2.waitKey(0)
plt.figure(figsize=(8,5))
plt.plot(np.arange(1,iteration+1),uniformity)
plt.xlabel("Iteration")
plt.ylabel("Uniformity")
plt.ylim(0,1)
if __name__ == "__main__":
main()
ここで、レンズ透過前のレーザーは強度が一様だとし、レンズ透過後のレーザーは画像のように10×10の点に分岐して欲しいとします(元画像リンク)。

上記の条件で、プログラムを実行すると以下のような位相画像が取得できます。

これは CGH(計算機ホログラム) と呼ばれます。(光の分野ではホログラムという名前はこれ以外にも使うものですので注意してください。めっちゃややこしいです。)
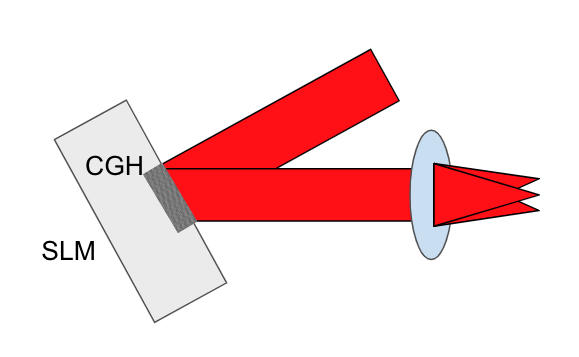
このCGHを、画像のように SLM という光の位相を制御できる装置に表示し、そこにレーザーを当てて、レンズを通すとあら不思議、自分の欲しかった形にレーザーが分岐していることでしょう。
面倒な加工も一瞬で終わりますね!
ちなみにプログラム上でのrecはこのCGHを使用した場合のシミュレーション上での再構成結果になります。
Uniformityはこの再構成結果の分岐した各点の強度の均一性を表しています。
今回10×10に分岐したレーザーの強度はすべて同じになっていて欲しかったのですが、Uniformityや再構成結果を見るとそうはなっていないことがわかると思います(一定以上の繰り返し後はUniformityが飽和してしまう)。
実際、作成したCGHを使用しても再構成像と同様に均一にはならないです。
今回は紹介を省きますが、この均一性を高めるために 重み付けアルゴリズム をはじめとした様々な手法が考案されています。
興味のある方はぜひそちらも調べてみてください。
終わりに
レーザーで何本も線を引かなければならなかったり、大量に穴を開ける必要があって面倒だったそこのあなた!
ぜひこのフーリエ反復法で得られるCGHを使ってレーザーを分岐させちゃってください!
ちなみに機材はないけどこの手法を実際に試してみたい方! レーザーは3000万?SLMは30万円?くらいで売っていたはずなのでぜひ購入して試してみてください!
以上で僕の担当記事を終わります!
この記事を読んで「面白かった」「学びがあった」と思っていただけた方、よろしければ Twitter や facebook、はてなブックマークにてコメントをお願いします!
また DeNA 公式 Twitter アカウント @DeNAxTech では、 Blog記事だけでなく色々な勉強会での登壇資料も発信してます。ぜひフォローして下さい!